Календарно-тематическое планирование по алгебре
реклама
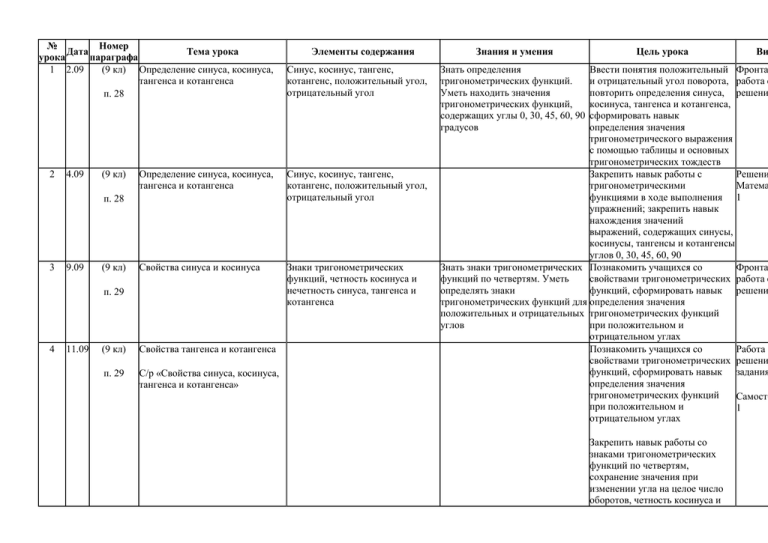
№ Номер Дата Тема урока урока параграфа 1 2.09 (9 кл) Определение синуса, косинуса, тангенса и котангенса п. 28 2 4.09 (9 кл) 9.09 (9 кл) Синус, косинус, тангенс, котангенс, положительный угол, отрицательный угол Свойства синуса и косинуса Знаки тригонометрических функций, четность косинуса и нечетность синуса, тангенса и котангенса п. 29 4 11.09 Синус, косинус, тангенс, котангенс, положительный угол, отрицательный угол Определение синуса, косинуса, тангенса и котангенса п. 28 3 Элементы содержания (9 кл) Свойства тангенса и котангенса п. 29 С/р «Свойства синуса, косинуса, тангенса и котангенса» Знания и умения Цель урока Знать определения тригонометрических функций. Уметь находить значения тригонометрических функций, содержащих углы 0, 30, 45, 60, 90 градусов Ви Ввести понятия положительный Фронта и отрицательный угол поворота, работа с повторить определения синуса, решени косинуса, тангенса и котангенса, сформировать навык определения значения тригонометрического выражения с помощью таблицы и основных тригонометрических тождеств Закрепить навык работы с Решени тригонометрическими Матема функциями в ходе выполнения 1 упражнений; закрепить навык нахождения значений выражений, содержащих синусы, косинусы, тангенсы и котангенсы углов 0, 30, 45, 60, 90 Знать знаки тригонометрических Познакомить учащихся со Фронта функций по четвертям. Уметь свойствами тригонометрических работа с определять знаки функций, сформировать навык решени тригонометрических функций для определения значения положительных и отрицательных тригонометрических функций углов при положительном и отрицательном углах Познакомить учащихся со Работа с свойствами тригонометрических решени функций, сформировать навык задания определения значения тригонометрических функций Самосто при положительном и 1 отрицательном углах Закрепить навык работы со знаками тригонометрических функций по четвертям, сохранение значения при изменении угла на целое число оборотов, четность косинуса и 5 16.09 (9 кл) Радианная мера угла Градусная мера угла, радианная мера угла Радианная мера угла Градусная мера угла, радианная мера угла п. 30 6 7 18.09 (9 кл) 23.09 п. 30 (9 кл) п. 31 8 25.09 (9 кл) п. 31 Соотношения между Основное тригонометрическое тригонометрическими тождество, тригонометрические функциями одного и того же угла тождества Соотношения между тригонометрическими функциями одного и того же угла С/р « Соотношения между тригонометрическими функциями одного и того же угла» 9 30.09 (9 кл) п. 32 10 2.10 (9 кл) п. 32 Применение основных тригонометрических формул к преобразованию выражений Тригонометрические тождества Применение основных тригонометрических формул к преобразованию выражений Тригонометрические тождества нечетность синуса, тангенса и котангенса Уметь выполнять переход от Ввести понятие единицы Опрос, радианной меры угла к градусной измерения углов – радиан, учебник мере и наоборот познакомить с формулой задач перевода из градусной меры в радианную, научить применять формулу на практике Уметь выполнять переход от Закрепить умения выполнять Решени радианной меры угла к градусной переход от радианной меры угла Матема мере и наоборот к градусной мере и наоборот 2 Уметь находить значения Познакомить учащихся с Фронта тригонометрических функций по основными работа с известному значению одной из тригонометрическими решени них тождествами, сформировать навык применения тригонометрических тождеств при упрощении тригонометрических выражений Сформировать умения вычислять Матема значения тригонометрических 3 (Инди функций по известному разноур значению одной из них Самосто Закрепить навык применения 2 тригонометрических тождеств при вычислении значения тригонометрического выражения и при упрощении тригонометрических выражений Уметь применять Рассмотреть более сложные Решени тригонометрические тождества примеры преобразования задания для преобразования выражений тригонометрических выражений с применением основных тригонометрических тождеств, сформировать навык преобразования выражений Уметь применять Выработать умения и навыки Решени тригонометрические тождества выполнять несложные задания преобразования для преобразования тригонометрических выражений выражений. Уметь находить значения тригонометрических функций по известному значению одной из них 11 7.10 12 9.10 (9 кл) Тригонометрические тождества п. 32 Применение основных тригонометрических формул к преобразованию выражений (9 кл) Формулы приведения Формулы приведения (9 кл) Формулы приведения Формулы приведения п. 33 С/р «Формулы приведения» п. 33 13 14.10 14 16.10 15 21.10 (9 кл) Контрольная работа №1 «Тригонометрические функции. Тригонометрические формулы» Формулы сложения тригонометрических функций Тригонометрические функции. Тригонометрические формулы. Формулы сложения тригонометрических функций Формулы сложения для синуса, косинуса и тангенса Формулы сложения для синуса, косинуса и тангенса п. 34 16 23.10 (9 кл) Закрепить навык преобразования Решени тригонометрических выражений задания с применение основных тригонометрических тождеств Знать правила преобразования Познакомить учащихся с Фронта тригонометрических выражений с формулами приведения и работа с помощью формул приведения. научить применять данные решени Уметь выполнять преобразования формулы при выполнении уравнений Уметь выполнять преобразования тригонометрических выражений Отработать навык работы с Решени формулами при упрощении выражений; способствовать Самосто развитию логического мышления 4 Закрепить навык преобразования тригонометрических выражений, содержащих формулы приведения Уметь применять Проверить степень усвоения Контрол тригонометрические формулы учащимися материала по данной для преобразования теме Знать формулы сложения Познакомить учащихся с Работа с тригонометрических функций. формулами сложения для синуса решени Уметь применять формулы для и косинуса и их следствиями, преобразования сформировать навык тригонометрических выражений преобразования тригонометрических выражений с использованием формул сложения Закрепить навык преобразования Решени тригонометрических выражений Матема с использованием формул 4 п. 34 17 28.10 (9 кл) Формулы двойного аргумента тригонометрических функций Формулы двойного угла Формулы двойного аргумента тригонометрических функций Формулы двойного угла п. 35 18 30.10 (9 кл) п. 35 Формулы суммы и разности тригонометрических функций Формулы суммы и разности синусов и косинусов Формулы суммы и разности тригонометрических функций Формулы суммы и разности синусов и косинусов Решени Матема 5 Работа с Решени Работа с решени 21 18.11 (9 кл) Синус, косинус, тангенс, котангенс (повторение) Уметь применять формулы при преобразовании выражений 22 20.11 (9 кл) Синус, косинус, тангенс, котангенс (повторение) Уметь применять формулы при преобразовании выражений Закрепить навык применения формул п. 36 20 13.11 (9 кл) Знать формулы суммы и разности синусов и косинусов. Уметь применять формулы для преобразования тригонометрических выражений Работа с решени Познакомить учащихся с формулами суммы и разности тригонометрических функций, сформировать навык применения формул на практике Сформировать навык Работа с применения формул суммы и решени разности при преобразовании тригонометрических выражений и доказательстве тождеств Закрепить навык применения формул 19 11.11 (9 кл) сложения, провести промежуточную проверку степени усвоения материала Знать формулы двойного Познакомить учащихся с аргумента. Уметь применять формулами двойного угла, формулы для преобразования сформировать навык преобразования тригонометрических выражений тригонометрических выражений Закрепить навык преобразования тригонометрических выражений с использованием формул двойного угла п. 36 23 25.11 §1 п.2 (1,2) Тригонометрические функции и График функций синус, косинус, их графики (синус, косинус) область определения, область значений функций 24 27.11 §1 п.2 (1,2) Тригонометрические функции и Графики функций тангенс, их графики (тангенс, котангенс) котангенс, область определения, область значений функции, Уметь строить график функций Ввести понятие числовой Работа с синус, косинус. Уметь определять функции синус, косинус; научить решени ООФ, ОЗФ выполнять построение данных графиков функций; находить область определения и область значения функций Уметь строить графики функций Ввести понятие числовой Работа с тангенс и котангенс. Уметь функции тангенс и котангенс; решени определять ООФ, ОЗФ, научить выполнять построение 25 2.12 Контрольная работа № 2 26 4.12 §2 п.3(1,2) Функции и их графики. 27 9.12 §2 п.3(2) Функции и их графики. 28 11.12 §2 п.4(1) Четные и нечетные функции. 29 16.12 §2 п.4(2) Четные и нечетные функции. Периодичность Периодичность тригонометрических функций 30 18.12 §2 п.5 Возрастание и убывание функций. Экстремумы асимптота значений функции асимптоты Параллельный перенос, растяжение вдоль оси с коэффициентом Уметь строить графики функций. Закрепить навык построения Работа с Знать основные преобразования тригонометрических функций; решени графиков функций познакомить с преобразованиями графиков ( параллельный перенос вдоль оси ординат, растяжение вдоль оси Оу с коэффициентом k, параллельный перенос вдоль оси абсцисс, растяжение вдоль оси Ох с коэффициентом k) Закрепить навык работы над Решени преобразованием графиков Матема тригонометрических функций 7 Знать свойства четных и Рассмотреть понятия четной и Работа с нечетных функции. Уметь нечетной функций, решени строить графики функций расположение их графиков; построе способствовать развитию навыков построения графиков функций Уметь вычислять значение Способствовать развитию Решени функции, используя ее четность навыков построения графиков ЕГЭ) или нечетность четных и нечетных функций. Сформировать навык решения Работа с практических задач без Уметь определять период решени использования графиков функции. Параллельный перенос, растяжение вдоль оси с коэффициентом, период Четность функции, нечетность функции Четность функции, нечетность функции, период Период тригонометрической функции, наименьший положительный период Промежутки возрастания, промежутки убывания, экстремумы Знать определения промежуток возрастания, промежуток убывания, экстремум, данных графиков функции; находить область определения и область значения функций Ввести определение периодической функции и доказать периодичность тригонометрических функций; научить находить наименьший положительный период функции Ввести понятия возрастания и Работа с убывания функций, экстремумов решени функции, учить применять эти понятия при чтении и 31 23.12 §2 п.5 Возрастание и убывание функций. Экстремумы 32 25.12 §2 п.6 Исследование функций 33 13.01 §2 п.6 Исследование функций 34 15.01 §2 п.6 Исследование функций 35 16.01 §2 п.7 Свойства тригонометрических функций. 36 20.01 §2 п.7 Свойства тригонометрических функций. 37 22.01 38 23.01 §3 п.8 39 27.01 §3 п.8 Контрольная работа № 3 Арксинус, арккосинус и арктангенс построении графиков функций Способствовать развитию навыков нахождения промежутков возрастания и убывания функции, ее максимумов и минимумов Схема исследования функции: Уметь по формуле исследовать Способствовать развитию ОДЗ, ОЗФ, промежутки функцию и строить ее график навыков чтения графиков и возрастания и убы вания, построения графиков функций, экстремумы, используя схему исследования функций точка максимума, точка минимума, Уметь по формуле исследовать Выработать навыки максимум, минимум, период, функцию и строить ее график исследования функции и четность, нечетность функции построения ее графика на основе выявленных свойств (ОДЗ, ООФ, промежутки возрастания и убывания, экстремумы) Выработать навыки исследования функции и построения ее графика Схема исследования Уметь исследовать Закрепить знание учащимися тригонометрических функций. тригонометрические функции. свойств тригонометрических Уметь применять свойства функций при исследовании тригонометрических функций при функций и построении графиков решении задач Закрепить знание учащимися свойств тригонометрических функций при исследовании функций и построении графиков Промежутки возрастания, промежутки убывания, экстремумы Арксинус, арккосинус и арктангенс Нахождение значений арксинуса, Арксинус, арккосинус и арккосинуса и арктангенса арктангенс С/р « Арксинус, арккосинус и Арксинус, арккосинус и максимум, минимум, точка максимума, точка минимума Знать определения арксинуса, арктангенса, арккотангенса. Уметь находить их значения Решени Матема 8 Решени Решени Решени Работа с решени Работа с решени Контрол Работа с решени Доказать теорему о корне и рассмотреть ее применения. Ввести понятия арксинус, арккосинус, арктангенс, арккотангенс; научить вычислять их значения Уметь находить значения Закрепить понятия арксинус, Решени арксинуса, арктангенса, арккосинус, арктангенс, арккотангенса с помощью таблиц арккотангенс и навыки Самосто вычисления их при решении 7 арктангенс» арктангенс более сложных упражнений. Научить пользоваться таблицами и микрокалькулятором для вычисления значений арксинуса, арккосинуса, арктангенса, арккотангенса. 40 29.01 §3 п.9 Решение простейших Формулы решений простейших Знать формулы корней Ввести формулы корней Работа с тригонометрических уравнений уравнений простейших тригонометрических простейших тригонометрических решени уравнений. Знать особые формы уравнений вида sinх=а, cosх=а, записи корней простейших tgх=а и рассмотреть примеры тригонометрических уравнений. решений простейших Уметь применять формулы при тригонометрических уравнений решении простейших тригонометрических уравнений 41 30.01 §3 п.9 Решение простейших Формулы решений простейших Знать формулы корней Проверить знание учащимися Работа с тригонометрических уравнений уравнений простейших тригонометрических формул корней простейших решени уравнений. Знать особые формы тригонометрических уравнений и записи корней простейших особую форму записи решений тригонометрических уравнений. уравнений. Закрепить навыки Уметь применять формулы при решения уравнений решении простейших тригонометрических уравнений 42 3.02 §3 п.10 Решение простейших Схема решения неравенств вида Знать приемы для решения На конкретных примерах с Работа с тригонометрических неравенств sinх<а, cosх<а, tgх<а, sinх>а, тригонометрических неравенств. помощью единичной окружности решени cosх>а, tgх>а Уметь решать простейшие показать решение простейших тригонометрические неравенства неравенств вида sinх<а, cosх<а, tgх<а, sinх>а, cosх>а, tgх>а .Научить решать такие неравенства. 43 5.02 §3 п.10 Решение простейших Закрепить навык решения Работа с тригонометрических неравенств тригонометрических неравенств решени на более сложных примерах 44 6.02 §3 п.11 Решение тригонометрических Формулы корней простейших Уметь решать тригономет. Рассмотреть решение Решени уравнений, приводимых к тригонометрических уравнений, уравнения, приводимые к тригонометрических уравнений, Матема квадратному корней квадратного ур-ия квадратным, и методом приводимых к квадратному, а 9 группировки также методом группировки и разложением на множители 45 10.02 §3 п.11 Решение однородных Однородное тригонометрическое Уметь решать однородные Рассмотреть решение Решени тригонометрических уравнений уравнение тригонометрические уравнения однородных тригонометрических уравнений и уравнений 46 12.02 §3 п.11 Решение тригонометрических Тригонометрические тождества, уравнений, решаемых с помощью формулы сложения формул сложения и понижения степени 47 13.02 §3 п.11 С/р «Примеры решения Формулы корней тригонометрических урав-ний» тригонометрических уравнений 48 17.02 Контрольная работа № 4 49 19.02 §4 п.12 Приращение функции 50 20.02 §4 п.12 Приращение функции Уметь решать уравнения с помощью формул сложения и понижения степени Уметь решать тригонометрические уравнения Приращение аргумента, приращение функции, угловой коэффициент Уметь определять приращение функции по графику и аналитически Приращение аргумента, приращение функции, угловой коэффициент Уметь определять приращение функции по графику и аналитически . 51 24.02 §4 п.13 Понятие о производной Производная, угловой коэффициент Уметь определять угловой коэффициент по углу наклона касательной приводимых к ним. Рассмотреть тригонометрические Решени уравнения, решаемые с помощью формул сложения, понижения степени и других Способствовать развитию Самосто навыков самостоятельного 9 применения знаний при решении тригонометрических уравнений Контрол Ввести понятия приращение Работа с аргумента и приращение решени функции; выработка умения вычисления их отношений, а также углового коэффициента секущей и средней скорости Сформировать навык Решени нахождения углового задания коэффициента секущей к графику функции Работа с решени Способствовать закреплению Решени наглядных образов касательной и задания производной; выработка навыка ЕГЭ)Ма нахождения производной по диктант определению 52 26.02 §4 п.14 Понятие о непрерывности и Непрерывность функции, Уметь определять является ли Познакомить учащихся с Работа с предельном переходе предельный переход функция непрерывной по графику понятиями предельный переход, решени и аналитически. Уметь непрерывность функции в точке определять к какому числу и правилами предельного стремится функция перехода; закрепить их при решении упражнений 53 27.02 §4 п.15 Правила вычисления Правила дифференцирования: Знать три основных правила Ввести правило Решени производных. Основные правила производные суммы, дифференцирования. Уметь дифференцирования суммы, учебник дифференцирования произведения, частного применять правила при решении доказать лемму и рассмотреть задач вывод формул дифференцируемости произведения, частного, степени 54 3.03 §4 п.15 Правила вычисления Правило вычисления производной Уметь вычислять производную Научить применять правила Работа с 55 5.03 56 6.03 производных. Производная степенной функции §4 п.15 Правила вычисления производных: решение задач 58 13.03 §4 п.17 Производные тригонометрических функций 59 17.03 §4 п.17 Производные тригонометрических функций 60 19.03 Контрольная работа № 5 61 20.03 §5 п.18 Применение непрерывности функции: метод интервалов 63 9.04 степенной функции нахождения производной Решени Уметь вычислять производные по Закрепление правил нахождения Решени правилам дифференцирования производных в ходе решения упражнений §4 п.16 Производная сложной функции. Правило вычисления производной Уметь находить производную Ввести понятие сложной Работа с сложной функции сложной функции функции и правило нахождения Решени ее производной Степенная функция. 57 12.03 §4 п.17 Производные тригонометрических функций 62 7.04 степенной функции Правила дифференцирования Правила вычисления производных сложных тригонометрических функций Правила вычисления производных сложных и тригонометрических функций Уметь вычислять производные сложных тригонометрических функций Уметь вычислять производные сложных и тригонометрических функций Правила вычисления производных Уметь вычислять производные сложных и тригонометрических сложных и тригонометрических функций функций Непрерывность функции, метод интервалов Уметь решать неравенства методом интервалов Сформировать навык нахождения производной сложной функции. Закрепить навык нахождения производных тригонометрических функций Проверить навык нахождения производной тригонометрических функций; скорректировать знания учащихся Проверить навык нахождения производной тригонометрических функций; скорректировать знания учащихся Ввести понятие непрерывности функции на промежутке, рассмотреть ее свойство знакопостоянства. Рассмотреть решение неравенств методом интервалов §5 п.18 Применение непрерывности Область определения непрерывной Уметь находить область Рассмотреть примеры функций, функции: область определения функции определения непрерывной не являющимися непрерывными, функции, используя метод а также примеры непрерывных, интервалов. но не дифференцируемых в данной точке §5 п.19 Касательная к графику функции: Геометрический смысл Уметь использовать Ввести определение касательной геометрический смысл производной геометрический смысл и сформулировать, в чем состоит производной производной при решении задач геометрический смысл Решени Решени Матема 12 Решени Матема 12 Контрол Работа с решени Работа с решени Работа с решени задания производной Ввести уравнение касательной к Работа с графику функции и научить решени находить его для конкретных функций. рассмотреть формулу Лагранжа Формула Лагранжа Уметь использовать Рассмотреть более сложные Решени геометрический смысл примеры и проверить навыки и математ производной и уравнение умения при самостоятельном 13 касательной при решении задач решении упражнений Механический смысл производной Знать механический смысл Дать понятие о возможностях Работа с производной. Уметь применять применения дифференциального решени при решении задач исчисления в описании и изучении процессов и явлений реального мира Механический смысл производной Уметь применять механический Показать широкий спектр Решени смысл производной при решении приложений производной математ задач 14 Применение признака возрастания Знать признак возрастания Доказать достаточный признак Работа с (убывания) функции при решении (убывания) функции. Уметь возрастания (убывания) функции Решени задач использовать признак для и показать его применение при определения промежутков нахождении промежутков монотонности функции возрастания (убывания) функции Сформировать навык работы по Работа с нахождению промежутков Решени монотонности функции Уметь использовать признак для Закрепить изученный материал Решени опр-ния пр-ков монотонности ф- по нахождению промежутков ции монотонности функции Экстремум, необходимое условие Уметь находить критические Ввести понятие критических Решени экстремума, признак максимума точки степенной функции точек функции, точек функции, признак минимума экстремума; рассмотреть функции необходимое условие экстремума, признак максимума и минимума ф-ции Уметь находить критические Способствовать выработке Решени точки тригонометрической навыка отыскания экстремумов математ функции функции, развитию логического 15 мышления учащихся Признак максимума функции, Уметь находить критические Поверить умения по нахождению Самосто 64 10.04 §5 п.19 Касательная к графику функции: Уравнение касательной уравнение касательной 65 14.04 §5 п.19 Касательная к графику функции: формула Лагранжа 66 16.04 §5 п.21 Производная в физике и технике: механический смысл производной 67 17.04 §5 п.21 Производная в физике и технике: примеры применения производной 68 21.04 §6 п.22 Признак возрастания (убывания) функции 69 23.04 §6 п.22 Признак возрастания (убывания) функции 70 24.04 §6 п.22 Признак возрастания (убывания) функции 71 28.04 §6 п.23 Критические точки функции, максимумы и минимумы 72 30.04 §6 п.23 Критические точки функции, максимумы и минимумы 73 5.05 §6 п.23 С/р «Критические точки Уметь составлять уравнение касательной для функции функции, максимумы и минимумы» 74 7.05 §6 п.24 Примеры применения производной к исследованию функций 75 8.05 §6 п.24 Применение производной к исследованию функций 76 12.05 §6 п.24 Применение производной к исследованию функций 77 14.05 §6 п.25 Наибольшее и наименьшее значения функции 78 15.05 §6 п.25 Наибольшее и наименьшее значения функции 79 19.05 80-86 21, 22, 26, 28, 29.05 Контрольная работа № 6 Итоговое повторение признак минимума функции точки функции критических точек функции с 13 помощью производной; скорректировать знания учащихся Схема исследования функции, Уметь исследовать функцию с Повторить схему исследования Работа с признаки монотонности функции, помощью производной и стоить функции для построения ее Решени признаки экстремумов функции график функции по проведенному графика и рассмотреть исследованию исследование функции с помощью производной Отработать навык комплексного Решени исследования степенной функции с помощью производной и построение графиков функции Схема исследования Уметь исследовать Развивать навыки исследования Решени тригонометрической функции, тригонометрическую функцию с функций и построения графиков; признаки монотонности функции, помощью производной и стоить закрепить знания нахождения признаки экстремумов функции график функции по проведенному промежутков возрастания и исследованию убывания функции, экстремумов функции с помощью производной Наибольшее значение функции, Знать схему нахождения Рассмотреть применение метода Работа с наименьшее значение функции на наибольшего и наименьшего поиска наибольших и Решени заданном промежутке значения функции на заданном наименьших значений функции к промежутке. Уметь применять решению разнообразных при решении задач прикладных задач Закрепить знания учащихся по Решени нахождению наибольшего и наименьшего значения функции Контрол Повторение материала 10 класса Уметь применять полученные знания