3-7. На шелковых нитях длиной 50 см каждая, прикрепленных к... два одинаково заряженных шарика массой по 0,2 г каждый. Определить...
реклама
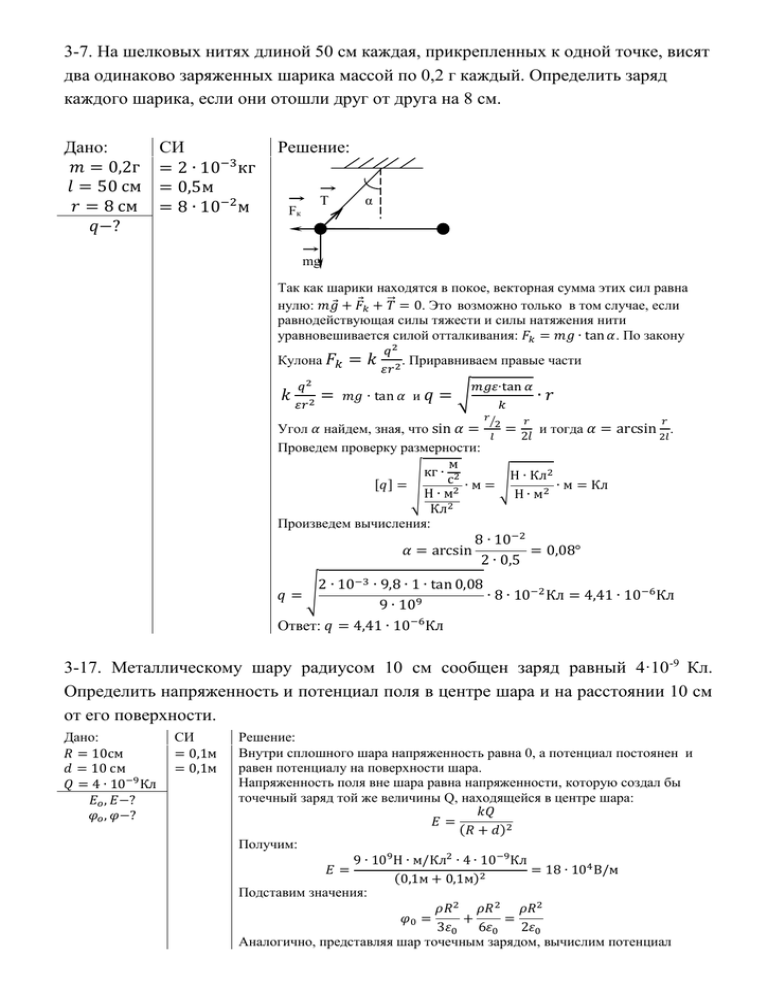
3-7. На шелковых нитях длиной 50 см каждая, прикрепленных к одной точке, висят два одинаково заряженных шарика массой по 0,2 г каждый. Определить заряд каждого шарика, если они отошли друг от друга на 8 см. Дано: 𝑚 = 0,2г 𝑙 = 50 см 𝑟 = 8 см 𝑞−? СИ = 2 ∙ 10−3 кг = 0,5м = 8 ∙ 10−2 м Решение: α T Fк mg Так как шарики находятся в покое, векторная сумма этих сил равна ⃗⃗ = 0. Это возможно только в том случае, если нулю: 𝑚𝑔⃗ + 𝐹⃗𝑘 + 𝑇 равнодействующая силы тяжести и силы натяжения нити уравновешивается силой отталкивания: 𝐹𝑘 = 𝑚𝑔 ∙ tan 𝛼. По закону Кулона 𝐹𝑘 𝑘 𝑞2 𝜀𝑟 2 = =𝑘 𝑞2 𝜀𝑟 2 . Приравниваем правые части 𝑚𝑔 ∙ tan 𝛼 и 𝑞 =√ 𝑚𝑔𝜀∙tan 𝛼 𝑘 𝑟⁄ ∙𝑟 𝑟 𝑟 Угол 𝛼 найдем, зная, что sin 𝛼 = 2 = и тогда 𝛼 = arcsin . 𝑙 2𝑙 2𝑙 Проведем проверку размерности: м кг ∙ 2 Н ∙ Кл2 с √ [𝑞] = √ ∙ м = ∙ м = Кл Н ∙ м2 Н ∙ м2 Кл2 Произведем вычисления: 𝛼 = arcsin 8 ∙ 10−2 = 0,08° 2 ∙ 0,5 2 ∙ 10−3 ∙ 9,8 ∙ 1 ∙ tan 0,08 ∙ 8 ∙ 10−2 Кл = 4,41 ∙ 10−6 Кл 9 9 ∙ 10 Ответ: 𝑞 = 4,41 ∙ 10−6 Кл 𝑞=√ 3-17. Металлическому шару радиусом 10 см сообщен заряд равный 4·10 -9 Кл. Определить напряженность и потенциал поля в центре шара и на расстоянии 10 см от его поверхности. Дано: 𝑅 = 10см 𝑑 = 10 см 𝑄 = 4 ∙ 10−9 Кл 𝐸𝑜 , 𝐸−? 𝜑𝑜 , 𝜑−? СИ = 0,1м = 0,1м Решение: Внутри сплошного шара напряженность равна 0, а потенциал постоянен и равен потенциалу на поверхности шара. Напряженность поля вне шара равна напряженности, которую создал бы точечный заряд той же величины Q, находящейся в центре шара: 𝑘𝑄 𝐸= (𝑅 + 𝑑)2 Получим: 9 ∙ 109 Н ∙ м/Кл2 ∙ 4 ∙ 10−9 Кл 𝐸= = 18 ∙ 104 В/м (0,1м + 0,1м)2 Подставим значения: 𝜌𝑅 2 𝜌𝑅 2 𝜌𝑅 2 𝜑0 = + = 3𝜀0 6𝜀0 2𝜀0 Аналогично, представляя шар точечным зарядом, вычислим потенциал поля: 𝑄 4𝜋𝜀𝜀0 (𝑅 + 𝑑) Вычислим в центре шара, подставив значения: 4 ∙ 10−9 Кл Кл 𝜑0 = = 0,9 ∙ 107 = 0,9 ∙ 107 В −12 4 ∙ 3,14 ∙ 1 ∙ 8,85 ∙ 10 Ф/м(0,1м + 0м) Ф Вычислим на расстоянии d, подставив значения: 4 ∙ 10−9 Кл Кл 𝜑= = 1,8 ∙ 107 = 1,8 ∙ 107 В −12 4 ∙ 3,14 ∙ 1 ∙ 8,85 ∙ 10 Ф/м(0,1м + 0,1м) Ф 𝜑= Ответ: 𝐸𝑜 = 0 𝐸 = 18 ∙ 104 В/м 𝜑0 = 0,9 ∙ 107 В 𝜑 = 1,8 ∙ 107 В 3-27. Плоский воздушный конденсатор с площадью пластин 30 см2 получил заряд 10-9 Кл. Определить ускорение электрона, пролетающего через такой конденсатор. Как изменится напряженность поля, если заполнить конденсатор парафином? Дано: СИ Решение: 𝑆 = 30см2 𝑄 = 10−9 Кл 𝑒 = 1,6 ∙ 10−19 Кл 𝑚 = 9,11 ∙ 10−31 кг 𝐸воздух −? 𝐸парафин 𝑎−? = 30 ∙ 10−4 м2 Поле конденсатора является однородным 𝐸 = 𝑐𝑜𝑛𝑠𝑡 В электрическом поле на электрон действует сила: 𝐹 = 𝑒𝐸 = 𝑐𝑜𝑛𝑠𝑡 где 𝑒 - заряд электрона. По второму закону Ньютона сила F сообщает постоянное ускорение: 𝐹 𝑎= 𝑚 Для однородного поля: 𝑈 𝐸= , 𝑑 где d – расстояние между пластинами. Напряжение на конденсаторе: 𝑄 𝑄 𝑄𝑑 𝑈= = = 𝜀 𝜀𝑆 𝐶 𝜀0 𝜀𝑆 0 ⁄ 𝑑 В плоском конденсаторе в промежутке между плоскостями напряженность равна 𝑄 𝐸= 2𝜀0 𝜀𝑆 Тогда 𝑄𝑒 𝐹= 𝜀0 𝜀𝑆 и 𝑄𝑒 𝑎= 𝜀0 𝜀𝑆𝑚 Кл ∙ Кл Дж м = = 2 Ф 2 м ∙ кг с м ∙ м ∙ кг Подставим значения: 10−9 ∙ 1,6 ∙ 10−19 м м 𝑎= = 6,62 ∙ 1015 2 −12 −3 −31 2 8,85 ∙ 10 ∙ 1 ∙ 3 ∙ 10 ∙ 9,11 ∙ 10 с с [𝑎] = Диэлектрические проницаемости воздуха и парафина: 𝜀воздух = 1 𝜀парафин = 2,3 Сравним напряженности: 𝑄 𝐸воздух = 2𝜀0 𝜀воздух 𝑆 𝑄 𝐸парафин = 2𝜀0 𝜀парафин 𝑆 Отсюда: 𝐸воздух 2𝜀0 𝜀парафин 𝑆 𝜀парафин 𝑄 = ∙ = = 2,3 𝐸парафин 2𝜀0 𝜀воздух 𝑆 𝑄 𝜀воздух Ответ: м 𝑎 = 6,62 ∙ 1015 2 с 𝐸воздух = 2,3 𝐸парафин 3-37. Сколько времени потребуется для нагревания воды объемом 2 л до кипения при начальной температуре 100С в электрическом чайнике с электронагревателем мощностью 1 кВт, если его КПД равен 90%? Какова сила тока в спирали нагревателя, если напряжение равно 220 В? Дано: СИ Решение: Количество теплоты, необходимое для нагревания воды в 𝑉 = 2л чайнике, определяется по формуле: 103 Дж 𝑄 = 𝑐𝑚∆𝑇, с = 4,2 ∙ кг ∙ К где: 𝑚 = 𝜌𝑉, ∆𝑇 = 𝑇2 − 𝑇1 , т.е.: = 283.15𝐾 𝑇1 = 10℃ 𝑄 = 𝑐𝜌𝑉(𝑇2 − 𝑇1 ). Оно связано с мощностью 𝑃 нагревателя, его КПД и = 373.15𝐾 𝑇2 = 100℃ временем 𝑡 выражением 𝜂 = 0,9 𝑄 = 𝜂𝑃𝑡 = 103 Вт P=1кВт Отсюда 𝑄 𝑐𝜌𝑉(𝑇2 − 𝑇1 ) 𝑈 = 220В 𝑡= = 𝜂𝑃 𝜂𝑃 𝑡, 𝐼−? Проведем проверку размерности Дж кг ∙ л (К − К) кг ∙К∙ л [𝑡] = =с Дж с 4,2 ∙ 103 ∙ 1 ∙ 2 ∙ (373,15 − 283,15) 𝑡= 𝑐 = 840 с. 0,9 ∙ 1000 Для нахождения силы тока выразим электрическую мощность через силу тока и напряжение: 𝑃 = 𝐼𝑈 Тогда 𝑃 𝐼= 𝑈 𝐼= Ответ: 𝑡 = 840 с 𝐼 = 4,5 А 1000 А ∙ В = 4,5 А 220 В 3-47. Какую силу тока показывает миллиамперметр (см.рис.4), если Е1 = 2,5 В, Е2= 8,5 В, R3 = 500 Ом, сопротивление миллиамперметра 200 Ом, а падение напряжения на сопротивлении R2 равно 1 В? Внутренним сопротивлением источников тока пренебречь. R1 E1 R2 mA R3 E2 Рис.4 Дано: Решение: Е1 = 2,5В Е2= 8,5В R3 = 500 Ом RА = 200 Ом U2=1В I3-? Применим правило Кирхгофа для контура через R2, миллиамперметр, Е2, R3: 𝐼2 𝑅2 + 𝐼3 𝑅𝐴 + 𝐼3 𝑅3 = 𝐸2 Подставим исходные данные: 1 + 200𝐼3 + 500𝐼3 = 8,5 700𝐼3 = 7,5 7,5 Тогда 𝐼3 = 700 А = 10мА Ответ: 10 мА 3-57. По двум тонким длинным параллельным проводам, расстояние между которыми 10 см, текут в одном направлении токи силой 3 А и 2 А. Определить индукцию и напряженность магнитного поля в точке, удаленной на расстояние 6 см от первого провода и на расстояние 8 см от второго провода, если провода находятся в воздухе. Дано: СИ 𝑑 = 10см 𝐼1 = 3А 𝐼2 = 2А 𝑟1 = 6см 𝑟2 = 8см 𝐵, Н−? Решение: −1 = 10 м = 6 ∙ 10−2 м = 8 ∙ 10−2 м Согласно принципа суперпозиции, результирующее поле определим с помощью теоремы косинусов 𝐵 = √𝐵12 + 𝐵22 − 2𝐵1 𝐵2 cos 𝛼 где 𝑟12 + 𝑟22 − 𝑑2 2𝑟1 𝑟2 Определим магнитное поле каждого тока по закону Био-Савара-Лапласа: 𝜇0 𝐼1 𝐵1 = 2𝜋𝑟1 𝜇0 𝐼2 𝐵2 = 2𝜋𝑟2 cos 𝛼 = 𝜇0 𝐼1 2 𝐼2 2 𝐼1 𝐼2 2 √ 𝐵= ( ) + ( ) − 2 2 (𝑟1 + 𝑟22 − 𝑑2 ) 2𝜋 𝑟1 𝑟2 𝑟1 𝑟2 Подставим значения: 𝐵= 1,26 ∙ 10−6 2 ∙ 3,14 × √( Гн м × 2 2 3А 2А 3А 2А ((6 ∙ 10−2 м)2 + (8 ∙ 10−2 м)2 − (10−1 м)2 ) = ) + ( ) − (6 ∙ 10−2 м)2 (8 ∙ 10−2 м)2 6 ∙ 10−2 м 8 ∙ 10−2 м = 1,12 ∙ 10−3 Тл Напряженность магнитного поля, созданного бесконечно длинным прямолинейным проводником, равно 𝐼 𝐻 = 2𝜋𝑟 . Аналогично, по принципу суперпозиции: 𝐻 = √𝐻12 + 𝐻22 − 2𝐻1 𝐻2 cos 𝛼 = 𝐵 = Н= 1 𝐼 2 𝐼 2 𝐼 𝐼 √( 1 ) + ( 2 ) − 12 22 (𝑟12 + 𝑟22 − 𝑑2 ) 2𝜋 𝑟1 𝑟2 𝑟1 𝑟2 1 × 2 ∙ 3,14 × √( 2 2 3А 2А 3А 2А ((6 ∙ 10−2 м)2 + (8 ∙ 10−2 м)2 − (10−1 м)2 ) = ) + ( ) − −2 −2 −2 2 (6 ∙ 10 м) (8 ∙ 10−2 м)2 6 ∙ 10 м 8 ∙ 10 м = 890А/м Ответ: 𝐵 = 1,12 ∙ 10−3 Тл, Н= 890А/м 3-67. При индукции магнитного поля 1 Тл на каждый кубический сантиметр железа приходится энергия поля 2·10-4Дж. Определить магнитную проницаемость железа. Дано: СИ Решение: 𝐵2 𝐵 = 1Тл 𝑤= 2𝜇0 𝜇 Дж Дж 𝑤 = 2 ∙ 10−4 3 = 200 3 Отсюда: м см 𝐵2 𝜇 = 𝜇−? 2𝜇 𝑤 Проведем проверку размерности 0 кг 2 ( ) Тл с2 А [𝜇] = = =1 Гн Дж кг ∙ м2 кг ∙ м2 ∙ м м3 с2 А2 ∙ с2 м м3 2 Подставим значения и вычислим результат: 12 𝜇= = 2 ∙ 103 2 ∙ 1,26 ∙ 10−6 ∙ 200 Ответ: 𝜇 = 2 ∙ 103 3-77. Протон и электрон, ускоренные одинаковой разностью потенциалов 1000 В, влетают в однородное магнитное поле перпендикулярно его силовым линиям. Во сколько раз радиус траектории движения протона больше радиуса траектории электрона? Дано: 𝑈1 = 𝑈2 = 1000В 𝑝, 𝑒 𝑅1 −? 𝑅2 Решение: v1 Fл1 v2 Fл2 R1 B R2 На частицы действует сила Лоренца Fл1=Bev1; Fл2=Bev2 По второму закону Ньютона Fл1=ma1=mv12/R1; Fл2=ma2=mv22/R2 Bev1=m1v12/R1 Be=m1v1/R1 2 Bev2=mv2 /R2 Be=m2v2/R2 v1=BeR1/m1 v2=BeR2/m2 Частица, прошедшая ускоряющую разность потенциалов U, приобретает кинетическую энергию Т = еU. По условию U1 = U2. Так как заряды частиц равны по абсолютному значению, то Т1=Т2 m1v12/2=m2v22/2; m1v12=m2v22 m1(BeR1/m1)2=m2(BeR2/m2)2 (BeR1)2/m1=(BeR2)2/m2 R12/m1=R22/m2 R1/R2=√m1/m2, где m1=1,672·10−27 кг — масса протона; m2=9,11·10−31 кг — масса электрона. R1 1,672 10 27 42,8. R2 9,11 10 31 Ответ: R1/R2 = 42,8 3-87. Однородное магнитной поле перпендикулярно плоскости кольца радиусом 1 см, изготовленного из медной проволоки диаметром 2 мм. С какой скоростью должно изменяться во времени магнитной поле, чтобы сила индукционного тока в кольце составила 10 А? Удельное сопротивление меди 17 нОм·м. Дано: СИ: Решение: 𝑟 = 1см 𝑑 = 2 мм 𝐼 = 10𝐴 𝜌 = 17 нОм м · 𝜕𝐵 −? 𝜕𝑡 = 10−2 м = 2 ∙ 10−3 м = 1,7 ∙ 10−8 Ом ∙ м Согласно закону электромагнитной индукции Фарадея 𝜕Ф 𝜀= 𝜕𝑡 Магнитный поток Ф равен: Ф = 𝐵𝑆кольцо Тогда 𝜕𝐵 𝜕𝐵 𝜀 = 𝑆кольцо = 𝜋𝑟 2 𝜕𝑡 𝜕𝑡 Сопротивление равно: 𝜌𝑙 8𝜌𝑟 𝑅= = 2 𝑆сеч 𝑑 Индуцированный ток в кольце: 𝜀 𝜋𝑟𝑑2 𝜕𝐵 𝐼= = 𝑅 8𝜌 𝜕𝑡 Отсюда 𝜕𝐵 𝜋𝑟𝑑2 𝐼 = 𝜕𝑡 8𝜌 Подставим значения: 𝜕𝐵 3,14 ∙ 10−2 м ∙ (2 ∙ 10−3 м)2 ∙ 10А м2 А = = 9,2 = 9,2 Тл/с 𝜕𝑡 8 ∙ 1,7 ∙ 10−8 Ом ∙ м Ом 𝜕𝐵 Ответ: 𝜕𝑡 = 9,2 Тл/с 3-97. Закрытый колебательный контур состоит из катушки индуктивности и конденсатора. Определить собственную частоту колебаний, возникающих в контуре, если максимальная сила тока в катушке индуктивности 1,2 А, максимальная разность потенциалов на обкладках конденсатора 1200 В, полная энергия контура 1,1 мДж. Дано: Решение: 𝐼 = 1,2А Выразим через 𝑊 = 𝐿𝐼2 2 и𝑊= 𝐶𝑈 2 : 2 𝑈 = 1200В 𝑊 = 1,1 ∙ 10−3 Дж 2𝑊 𝐼2 2𝑊 𝐶= 2 𝑈 𝐿= 𝜈−? Период колебаний: 𝑇 = 2𝜋√𝐿𝐶 Тогда 𝜈= 1 1 = = 𝑇 2𝜋√𝐿𝐶 Подставим значения: 1 2𝜋√ 2𝑊 2𝑊 ∙ 𝐼2 𝑈2 = 𝐼𝑈 4𝜋𝑊 1,2А ∙ 1200В = 1,04 ∙ 105 Гц 4 ∙ 3,14 ∙ 1,1 ∙ 10−3 Дж Ответ: 𝜈 = 1,04 ∙ 105 Гц 𝜈=



