Прямоугольный параллелепипед описан около цилиндра
реклама
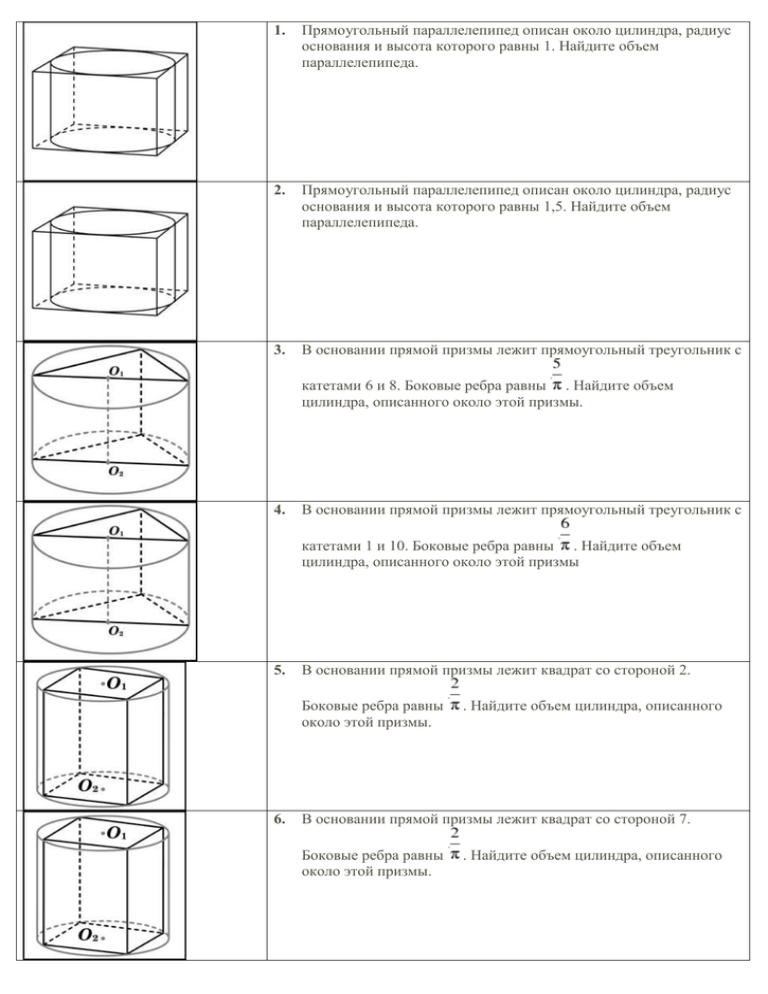
1. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда. 2. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1,5. Найдите объем параллелепипеда. 3. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. 4. В основании прямой призмы лежит прямоугольный треугольник с катетами 1 и 10. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы 5. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны около этой призмы. 6. . Найдите объем цилиндра, описанного В основании прямой призмы лежит квадрат со стороной 7. Боковые ребра равны около этой призмы. . Найдите объем цилиндра, описанного 7. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 23. 8. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 27. 9. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. 10. Объем конуса равен 168. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. 11. Площадь поверхности куба равна 18. Найдите его диагональ. 12. Объем куба равен 8. Найдите площадь его поверхности. 13. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10. 14. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на . 15. Площадь большого круга шара равна 3. Найдите площадь поверхности шара. 16. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ. 17. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба. 18. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10. 19. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760. 20. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. 21. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 2. 22. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 2. 23. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности. 24. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды. 25. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды. 26. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. 27. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза? 28. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба. 29. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара. 30. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). 31. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). 32. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). 33. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). 34. В основании прямой призмы лежит прямоугольный треугольник с катетами 8 и 11. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. 35. В основании прямой призмы лежит прямоугольный треугольник с катетами 9 и 12. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. 36. В основании прямой призмы лежит прямоугольный треугольник с катетами 9 и 14. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. 37. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 1, а высота — 8. 38. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 10, а высота — 5. 39. Стороны основания правильной шестиугольной пирамиды равны 20, боковые ребра равны 26. Найдите площадь боковой поверхности этой пирамиды. 40. Стороны основания правильной шестиугольной пирамиды равны 140, боковые ребра равны 74. Найдите площадь боковой поверхности этой пирамиды. 41. Стороны основания правильной шестиугольной пирамиды равны 48, боковые ребра равны 25. Найдите площадь боковой поверхности этой пирамиды. 42. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 20,5 раза? 43. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 12 раз? 44. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 12,5 раза? 45. Объем прямоугольного параллелепипеда, описанного около сферы, равен 15625. Найдите радиус сферы. 46. Объем прямоугольного параллелепипеда, описанного около сферы, равен 4096. Найдите радиус сферы. 47. Объем прямоугольного параллелепипеда, описанного около сферы, равен 2197. Найдите радиус сферы. 48. В правильной четырехугольной пирамиде высота равна 7, боковое ребро равно 13. Найдите ее объем. 49. В правильной четырехугольной пирамиде высота равна 5, боковое ребро равно 14. Найдите ее объем. 50. От треугольной пирамиды, объем которой равен 90, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды. 51. От треугольной пирамиды, объем которой равен 30, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды. 52. От треугольной пирамиды, объем которой равен 92, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды. 53. От треугольной пирамиды, объем которой равен 92, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды. 54. Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 11. Найдите его объем, деленный на . 55. Конус описан около правильной четырехугольной пирамиды со стороной основания 5 и высотой 9. Найдите его объем, деленный на . 56. Конус описан около правильной четырехугольной пирамиды со стороной основания 7 и высотой 9. Найдите его объем, деленный на . 57. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в 37 раз? 58. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в 15 раз? 59. Длина окружности основания конуса равна 7, образующая равна 6. Найдите площадь боковой поверхности конуса. 60. Длина окружности основания конуса равна 8, образующая равна 6. Найдите площадь боковой поверхности конуса. 61. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 10 и 10. Диагональ параллелепипеда равна 15. Найдите площадь поверхности параллелепипеда. 62. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 24. Диагональ параллелепипеда равна 26. Найдите площадь поверхности параллелепипеда. 63. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 10 и 24. Площадь ее поверхности равна 1140. Найдите высоту призмы. 64. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 10 и 24. Площадь ее поверхности равна 1500. Найдите высоту призмы. 65. Высота конуса равна 28, образующая равна 35. Найдите площадь его полной поверхности, деленную на . 66. Высота конуса равна 15, образующая равна 17. Найдите площадь его полной поверхности, деленную на . 67. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен , а высота равна 4. 68. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен , а высота равна 2. 69. Площадь осевого сечения цилиндра равна 18. Найдите площадь боковой поверхности цилиндра, деленную на . 70. Площадь осевого сечения цилиндра равна 1. Найдите площадь боковой поверхности цилиндра, деленную на . 71. Объем куба равен 44. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины. 72. Объем куба равен 24. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины. 73. Середина ребра куба со стороной 4,4 является центром шара радиуса 2,2. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите . 74. Середина ребра куба со стороной 2,3 является центром шара радиуса 1,15. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите . 75. Середина ребра куба со стороной 2 является центром шара радиуса 1. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите . 76. Объем тетраэдра равен 2,4. Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра. 77. Объем тетраэдра равен 2,1. Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.