Круглов Б.В. Оптимальная организация разработки

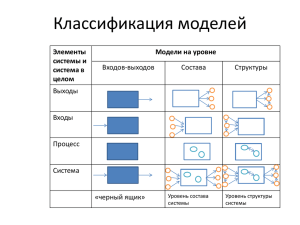
Круглов Б.В. Оптимальная организация разработки функциональных подсистем. //
Проблемы информатики в образовании, управлении, экономике и технике: Сб. статей Междунар. научно-техн. конф.– Пенза: ПДЗ, 2010. – С. 89-91.
ОПТИМАЛЬНАЯ ОРГАНИЗАЦИЯ РАЗРАБОТКИ
ФУНКЦИОНАЛЬНЫХ ПОДСИСТЕМ
Б.В. Круглов
ФНПЦ ОАО «НПО «Марс»,
г. Ульяновск, Россия
Доклад посвящен вопросам разработки проектной документации на функциональные системы (подсистемы). Рассматривается имитационная модель последовательной разработки
документов, позволяющая решить задачу о поиске оптимальной последовательности разработки.
Kruglov B.V. Optimal organization of the functional system development. The report deals
with the problems of design documentation development for the functional systems (subsystems). A
simulation model for solving the optimization problem of the coherent document development is
considered.
Создание в рамках электронного документооборота средств оптимальной
организации работ при проектировании иерархических АСУ позволяет сократить сроки и уменьшить затраты. В статье рассматривается задача проектирования функциональных систем (подсистем) иерархической АСУ, в основе решения которой лежит имитационная модель расчета времени разработки всех
документов при определенной последовательности, созданная автором.
Функциональные подсистемы ФП1, …, ФПm иерархической АСУ представляют собой информационные технологии и информационные ресурсы, обеспечивающие автоматизацию выделенных совокупностей функций должностных
лиц на всех уровнях управления АСУ. Каждая функциональная подсистема ФПi
имеет n составных частей по числу уровней управления ФПi1, ФПi2,…, ФПin
(рисунок).
Деление функциональных подсистем по уровням управления
Проектирование ФПi состоит из последовательных этапов проектирования
ФПi1 → ФПi2 → … → ФПin в общем случае различными группами с числом исполнителей R1, R2, … Rn. Время разработки каждой части определяется ее объемом Vij и числом исполнителей j-го уровня и их производительностью  ij :
tij   ij  Vij / Rij .
Время разработки m функциональных подсистем сложным образом зависит
от времени разработки каждой из частей с учетом запаздываний и ожиданий на
каждом уровне и последовательности разработки  :


T  tij ,  , i  1, m, j  1, n.
Выбирая определенную последовательность разработки функциональных
подсистем из множества возможных  , сокращаем время разработки всех проектов.
Имитационная модель отражает реальное делопроизводство: в организацию,
состоящую из нескольких групп сотрудников, поступает поток документов. Если группа свободна, она начинает разработку очередного документа в течение
некоторого времени, после чего переходит в состояние ожидания следующего
документа. Деятельность групп разработчиков представляет собой n зависимых
процессов: различные группы не могут одновременно разрабатывать один и тот
же документ, и при этом i-я группа может разрабатывать только свою часть документа. Имитационный эксперимент прекращается, когда разработана последняя часть последнего документа. Всего разрабатывается nm частей документов,
следовательно, система принимает 2nm состояний.
Обозначим время полной разработки документации для заданной очередности документов за Tимитации ( ) . Тогда задачу нахождения оптимального расписания можно поставить в виде последовательности операторов [1]:


 D1  B



B


 D2 
Tимитации ( )   A1  A2  B  C  
 E  t
 min,
ij , 
 ...




 D( 2 nm)  E



где   1, 2 ,..., M  – множество расписаний последовательностей разработки документов; A1 – оператор задания начальных условий для моделируемого варианта (объем работы и коэффициент трудоемкости для каждой части каждого
документа); A2 – оператор задания начальных условий для одного имитационного эксперимента; B – оператор определения очередного момента изменения
состояния системы; C – логический оператор, в соответствии с наступившим
событием осуществляющий переход к соответствующему оператору Di, имитирующему реакцию системы на события.
Правильность результатов, полученных с помощью имитационного моделирования, проверялась формулой, известной из теории расписаний [2, с. 168].
Имитационное моделирование позволяет сравнительно легко на основе решения задачи оптимального расписания поставить и решить более важную задачу
распределения ресурсов по уровням при ограничении на их общее число.
Библиографический список
1. Денисов А.А., Колесников Д.Н. Теория больших систем управления: учеб.
пособие для вузов. – Л.: Энергоиздат, 1982. – 288 с.
2. Танаев В.С., Шкурба В.В. Введение в теорию расписаний. – М.: Наука,
1975. – 256 с.