Арефьева И. Г., Адамович Т.А. 10 класс

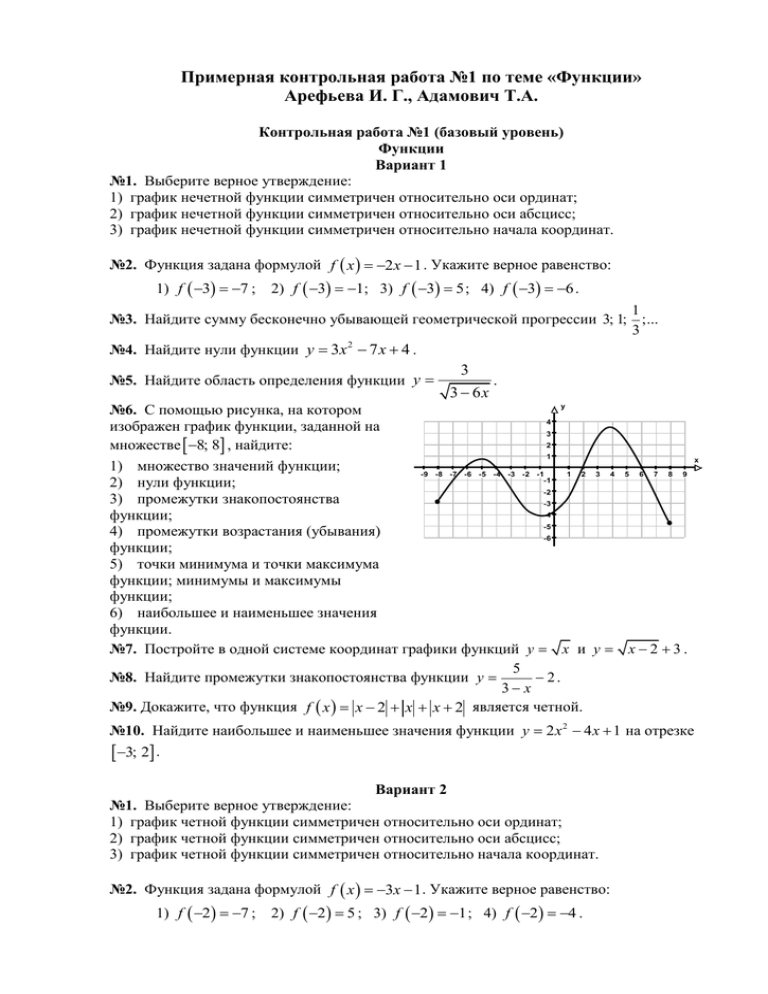
Примерная контрольная работа №1 по теме «Функции»
Арефьева И. Г., Адамович Т.А.
Контрольная работа №1 (базовый уровень)
Функции
Вариант 1
№1. Выберите верное утверждение:
1) график нечетной функции симметричен относительно оси ординат;
2) график нечетной функции симметричен относительно оси абсцисс;
3) график нечетной функции симметричен относительно начала координат.
№2. Функция задана формулой f  x   2 x  1 . Укажите верное равенство:
1) f  3  7 ;
2) f  3  1; 3) f  3  5 ; 4) f  3  6 .
1
№3. Найдите сумму бесконечно убывающей геометрической прогрессии 3; 1; ;...
3
2
№4. Найдите нули функции y  3x  7 x  4 .
№5. Найдите область определения функции y 
3
3  6x
.
y
№6. С помощью рисунка, на котором
4
изображен график функции, заданной на
3
2
множестве  8; 8 , найдите:
1
1) множество значений функции;
-9 -8 -7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7 8 9
-1
2) нули функции;
-2
3) промежутки знакопостоянства
-3
-4
функции;
-5
4) промежутки возрастания (убывания)
-6
функции;
5) точки минимума и точки максимума
функции; минимумы и максимумы
функции;
6) наибольшее и наименьшее значения
функции.
№7. Постройте в одной системе координат графики функций y  x и y  x  2  3 .
5
 2.
№8. Найдите промежутки знакопостоянства функции y 
3 x
№9. Докажите, что функция f  x   x  2  x  x  2 является четной.
№10. Найдите наибольшее и наименьшее значения функции y  2 x 2  4 x  1 на отрезке
 3; 2 .
Вариант 2
№1. Выберите верное утверждение:
1) график четной функции симметричен относительно оси ординат;
2) график четной функции симметричен относительно оси абсцисс;
3) график четной функции симметричен относительно начала координат.
№2. Функция задана формулой f  x   3x  1. Укажите верное равенство:
1) f  2  7 ;
2) f  2  5 ; 3) f  2  1 ; 4) f  2  4 .
x
№3. Найдите сумму бесконечно убывающей геометрической прогрессии 4; 1;
1
;...
4
№4. Найдите нули функции y  5x 2  4 x  1
№5. Найдите область определения функции y 
№6. С помощью рисунка, на котором
изображен график функции, заданной на
множестве  8; 8 , найдите:
1) множество значений функции;
2) нули функции;
3) промежутки знакопостоянства
функции;
4) промежутки возрастания (убывания)
функции;
5) точки минимума и точки максимума
функции; минимумы и максимумы
функции;
6) наибольшее и наименьшее значения
функции.
7
2  4x
.
y
4
3
2
1
-9 -8 -7 -6 -5 -4 -3 -2 -1
-1
x
1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
№7. Постройте в одной системе координат графики функций y  x и y  x  3  2 .
№8. Найдите промежутки знакопостоянства функции y 
4
3.
5 x
№9. Докажите, что функция f  x    x  4 x  5   x  4 x  5 является нечетной.
№10. Найдите наибольшее и наименьшее значения функции y  3x 2  6 x  5 на отрезке
 1; 4 .
Контрольная работа №1 (повышенный уровень)
Функции
Вариант 1
№1. Укажите промежуток (объединение промежутков), который не может являться
областью определения четной функции:
1)  ; 0   0;    ; 2)  4;  2   2; 4 ; 3)  5; 6 ; 4)  8; 8 .
№2. Функция задана формулой f  x    x2  x . Укажите верное равенство:
1) f  3  6 ;
2) f  3  0 ; 3) f  3  12 ; 4) f  3  6 .
№3. Найдите наибольшее и наименьшее значения функции y   x  1 на отрезке  2; 5 .
№4. Найдите промежутки знакопостоянства функции y 
1
x4.
3
№5. Представьте в виде обыкновенной дроби число 0,5  7  .
№6. С помощью рисунка, на котором
изображен график функции, заданной на
множестве  8; 7 , найдите:
1) множество значений функции;
2) нули функции;
3) промежутки знакопостоянства
функции;
4) промежутки возрастания (убывания)
функции;
5) точки минимума и точки максимума
функции; минимумы и максимумы
функции;
6) наибольшее и наименьшее значения
функции.
y
4
3
2
1
x
-9 -8 -7 -6 -5 -4 -3 -2 -1
-1
1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
7
№7. Найдите область определения функции f  x   x 2  25 
x  3x  10
2
.
№8. График функции y  f  x  получен из графика функции g  x   4 x3 смещением его
на 3 единичных отрезка вправо вдоль оси абсцисс и на 7 единичных отрезов вниз вдоль
оси ординат. Найдите ординату точки пересечения графика функции y  f  x  и прямой
x  4.
№9. Дана функция f  x   x2  6x  8 . Постройте график функции y  f  x  .
№10. Найдите функцию, обратную функции y  x 2  4 x  6 , D  y    2;    .
Вариант 2
№1. Укажите промежуток (объединение промежутков), который не может являться
областью определения нечетной функции:
1)  5;  3   3; 5 ; 2)  8; 7 ; 3)  ; 0   0;    ; 4)  1; 1 .
№2. Функция задана формулой f  x    x2  x . Укажите верное равенство:
1) f  4  12 ;
2) f  4  20 ; 3) f  4  0 ; 4) f  4   12 .
№3. Найдите наибольшее и наименьшее значения функции y   x  2 на отрезке 1; 6 .
№4. Найдите промежутки знакопостоянства функции y 
1
x  9.
2
№5. Представьте в виде обыкновенной дроби число 0,7  4 .
y
№6. С помощью рисунка, на
5
котором изображен график функции,
4
3
заданной на множестве  6; 10 ,
2
найдите:
1
1) множество значений функции;
-7
-6 -5
-4
-3
-2
-1
1
2) нули функции;
-1
3) промежутки знакопостоянства
-2
-3
функции;
-4
4) промежутки возрастания
-5
(убывания) функции;
5) точки минимума и точки
x
2
3
4
5
6
7
8
9
10
11
максимума функции; минимумы и
максимумы функции;
6) наибольшее и наименьшее
значения функции.
№7. Найдите область определения функции f  x   x 2  16 
5
x  2x  8
2
.
№8. График функции y  f  x  получен из графика функции g  x   3x3 смещением его
на 4 единичных отрезка влево вдоль оси абсцисс и на 2 единичных отрезка вниз вдоль оси
ординат. Найдите ординату точки пересечения графика функции y  f  x  и прямой
x  5 .
№9. Дана функция f  x   x2  4x  3 . Постройте график функции y  f  x  .
№10. Найдите функцию, обратную функции y  x 2  6 x  10 , D  y   3;    .