Задачи по теме «Дифференциальная геометрия»

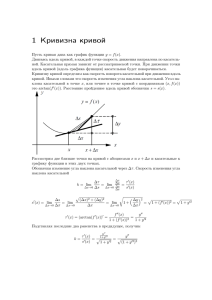
Задачи по теме «Дифференциальная геометрия»
1. Составить уравнения касательной прямой и нормальной плоскости к кривой
а) x  sec t ,
y  tg t , z  at, при t   / 4,
б) r (t )  (t , t , t ) в точке (1,1,1)
2
3
t
с) r (t )  (e , e , t ) при t=1,
t
2
2. Написать уравнение соприкасающейся плоскости кривой r (t )  ( a cos t , b sin t , e ) в
t
точке t=0.
3. Доказать, что для следующих кривых кривизна и кручение равны:
1) x=a ch t, y=a sh t, z=at;
2) x  3t  t , y  3t , z  3t  t .
3
2
3
4. В точке t=0 для винтовой линии r (t )  (a cost , a sin t , bt) записать уравнения
главной нормали; бинормали м соприкасающейся плоскости..
5. Найти кривизну и кручение кривой x  cos t , y  sin t , z  cos 2t.
3
3
6. Составить уравнение главной нормали и бинормали кривой:
x  t, y  t 2 , z  t 3
при t  1.
7. Найти кривизну и кручение в произвольной точке следующей кривой:

r (t )  (2t , ln t , t 2 ) .
2
8. Найдите точки на кривой x  , y  ln t , z  t 2 , в которых бинормаль параллельна
t
плоскости x  y  8 z  2  0 .
9. Написать естественную параметризацию кривой x  e t cos t , y  e t sin t , z  e t .
10. Доказать, что кривая r  r (t )  t 2  2t  3; 2t 2  t  1; 3t 2  5 плоская.


2
3
11. Дана кривая r  r (t )  (t , 1  t , t ) . Найти координаты вектора главной нормали и
бинормали в точке (0,1,0)..