Ключи (10 класс)

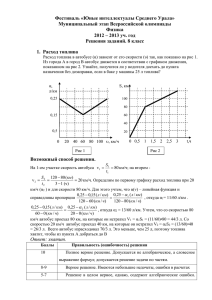
Ключи (10 класс)
Задание 1.(5 баллов)
В лифте находится ведро с водой, в котором плавает мяч. Как изменится глубина
погружения мяча, если лифт будет двигаться с ускорением a , направленным
вверх? вниз?
Решение:
При плавании мяча в воде в неподвижном лифте выполняется условие равновесия
mg   B gVB ,
где m– масса мяча, V – объем вытесненной воды, ρВ – ее плотность.
Когда лифт движется с ускорением, вес тела равен m(g ± а). Знак «плюс»
соответствует ускорению, направленному вверх, знак «минус» – ускорению,
направленному вниз. Однако при ускоренном движении лифта вес вытесненной
жидкости, а поэтому и сила Архимеда изменяется во столько же раз, во сколько
раз изменяется вес любого тела! Значит, равновесие сохранится без изменения
объема вытесненной воды VB.
B
Критерии оценивания
Получено решение с правильным ответом –6 баллов
Идея решения верна, но допущены ошибки в выводах – 4 балла.
Написаны условия плавания тел – 3 балла.
По усмотрению проверяющего, за разумные идеи или формулы – 2 балла.
Задание 2.(10 баллов)
Шарик, пущенный вверх по наклонной плоскости, проходит последовательно два
равных отрезка длиной l каждый и продолжает двигаться дальше. Первый отрезок
шарик прошел за t секунд, второй за 3t секунд. Найти скорость v шарика в конце
первого отрезка пути.
Решение:
a
l  v0 t  t 2
2 (1)
a
l  v0 (4t )  (4t ) 2
2
2
(2)
v  v0  at
(3)
5l
Совместное решение уравнений 1-3 дает ответ: v = 6 t .
Баллы
10
8-9
6-7
Правильность (ошибочность) решения
Полное верное решение, включающее правильный ответ.
Верное решение. Имеются небольшие недочеты, в целом не
влияющие на решение.
Решение в целом верное, содержит физические уравнения, но
3-5
1-2
0
не выполнены математические расчеты.
Не найдено одно из необходимых для решения уравнений, в
результате полученная система уравнений не полна и
невозможно найти решение.
Есть отдельные уравнения, относящиеся к сути задачи при
отсутствии решения (или при ошибочном решении).
Решение неверное, или отсутствует.
Задание 3.(10 баллов)
Сопротивления всех резисторов в цепи, схема которой
изображена на рисунке, одинаковы и равны R = 15 Ом.
Найдите сопротивление цепи между точками А иВ после
того, как был удалён проводник, соединявший
точки О´ и О´´
Решение задачи после удаления проводника, соединявшего точки О´ и О´´, сводится к простому применению правил расчёта сопротивлений
параллельно и последовательно соединённых резисторов (см. рисунок). Сопротивления нижней части схемы и середины верхней части одинаковы — это сопротивления параллельно соединённых резисторов R и 2R, так что
Последовательно с RСО´´D в верхней части схемы включено два резистора сопротивлениями по R, поэтому
. Поскольку
и
включены параллельно, то искомое сопротивление
Ответ:
Баллы
10
8-9
6-7
3-5
1-2
Правильность (ошибочность) решения
Полное верное решение, включающее правильный ответ.
Верное решение. Имеются небольшие недочеты, в целом не
влияющие на решение.
Решение в целом верное, содержит физические уравнения, но
не выполнены математические расчеты.
Не найдено одно из необходимых для решения уравнений, в
результате полученная система уравнений не полна и
невозможно найти решение.
Есть отдельные уравнения, относящиеся к сути задачи при
0
отсутствии решения (или при ошибочном решении).
Решение неверное, или отсутствует.
Всего 25 баллов