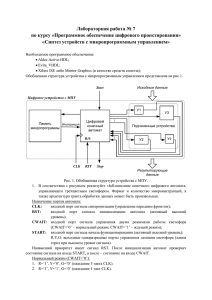
структура нечеткого контроллера

СТРУКТУРНАЯ МОДЕЛЬ НЕЧЕТКОГО КОНТРОЛЛЕРА
Козлов В.С.
В последнее время нечеткое моделирование является одной из наиболее
активных и перспективных направлений прикладных исследований в области
управления и принятия решений. Нечеткое моделирование оказывается
особенно полезным, когда в описании технических систем и бизнес-процессов
присутствует неопределенность, которая затрудняет или даже исключает
применение точных количественных методов и подходов.
В области управления техническими системами нечеткое моделирование
позволяет получать более адекватные результаты по сравнению с результатами,
которые основываются на использовании традиционных аналитических
моделей и алгоритмов управления. Диапазон применения нечетких методов с
каждым годом расширяется, охватывая такие области, как проектирование
промышленных роботов и бытовых электроприборов, управление доменными
печами и движение поездов метро, автоматическое распознавание речи и
изображений.
Нечеткая логика, которая служит основой для реализации методов
нечеткого управления, более естественно описывает характер человеческого
мышления и ход его рассуждений, чем традиционные формально-логические
системы. Именно поэтому изучение и использование математических средств
для представления нечеткой исходной информации позволяет строить модели,
которые наиболее адекватно отражают различные аспекты неопределенности,
постоянно присутствующей в окружающей нас реальности.
После первых промышленных приложений в Европе Япония за короткий
период времени вышла на первое место в мире по количеству устройств и
механизмов, в которых были реализованы нечеткие технологии. Появление
микропроцессоров и микроконтроллеров инициировало резкое увеличение
бытовых приборов и промышленных установок с алгоритмами управления на
основе нечеткой логики.
Имеется целый ряд обстоятельств, которые объясняют причины столь
впечатляющей популярности нечеткой логики в Японии. Во-первых, нечеткая
логика поддерживает разработку быстрого прототипа технического устройства
с последующим усложнением его функциональности, что характерно для стиля
работы японских инженеров. Во-вторых, нечеткая логическая модель более
проста для понимания, чем аналогичная математическая модель на основе
дифференциальных или разностных уравнений. В-третьих, нечеткие модели
оказываются более простыми для своей аппаратной реализации по сравнению с
классическими алгоритмами управления техническими системами.
В результате этого нечеткие технологии нашли свое применение в самых
различных технических устройствах и бытовых приборах, выпускаемых
японскими фирмами. Фотоаппараты и видеокамеры используют нечеткую
логику, чтобы реализовать опыт фотографа в управлении этими устройствами.
Например компании Fisher и Sanyo производят нечеткие логические
видеокамеры, в которых применяется нечеткая фокусировка и стабилизация
изображения.
Компания
используются
Matsushita
датчики
и
выпускает
стиральную
микропроцессоры
с
машину,
нечеткими
в
которой
алгоритмами
управления. Датчики определяют цвет и вид одежды, количество твердых
частиц, степень загрязнения, а нечеткий микропроцессор выбирает наиболее
подходящую программу стирки из 600 доступных комбинаций температуры
воды, количества стирального порошка и времени производственного цикла
быстрого или медленного вращения и промывки.
Компания Mitsubishi объявила о выпуске первого в мире автомобиля, где
управление каждой системой основано на нечеткой логике. При этом Mitsubishi
производит так же «нечеткий» кондиционер, который управляет изменением
температуры и влажности в помещении согласно человеческому восприятию
степени комфорта. Компания Nissan разработала «нечеткую» автоматическую
трансмиссию и «нечеткую» противоскользящую тормозную систему и
реализовала их в одном из своих последних автомобилей повышенной
комфортности.
Японский город Сендай имеет метрополитен с 16 станциями, который
управляется нечетким компьютером. При этом нечеткий компьютер процессы
3
ускорения и торможения поездов метро, делая на 70% меньше ошибок, чем
соответствующий человек-оператор.
4
ОСНОВЫ НЕЧЕТКОЙ ЛОГИКИ
Нечеткое множество
Базисное понятие нечетких систем - Нечеткое (под)множество. В
классической математике мы в основном используем четкие множество.
Для примера:
Сначала мы рассмотрим множество X всех вещественных чисел между 0 и
10, которые мы назовем областью исследования. Теперь, давайте определим
подмножество X всех вещественных чисел в амплитуде между 5 и 8.
A = [5,8]
Теперь представим множество A с помощью символической функции, т.е.
эта функция приписывает число 1 или 0 к каждому элементу в X, в зависимости
от того, находится ли элемент в подмножестве А или нет. Это приводит к
следующей диаграмме:
Мы можем интерпретировать элементы, которым назначено число 1, как
элементы которые находятся в множестве А и элементы, которым назначено
число 0, как элементы не в множестве A.
Этой концепции достаточно для многих областей приложений. Но мы
можем легко найти ситуации, где теряется гибкость. Чтобы показать это
рассмотрим следующий пример:
В этом примере мы хотим описать множество молодых людей. Более
формально мы можем обозначить
B = {множество молодых людей}
Поскольку, вообще, возраст начинается с 0, нижняя граница этого
множества должна быть нулевой. Верхнюю границу, с другой стороны, надо
5
определить. На первый раз определим верхнюю границу множества, скажем, 20
лет. Следовательно, мы получаем B как четкий интервал, а именно:
B = [0,20]
Теперь возникает вопрос: почему кто-то на его 20-ом дне рождения
молодой, а на следующий день не молодой? Очевидно, это - структурная
проблема, поскольку, если мы перемещаем верхнюю границу от 20 до
произвольной точки, мы можем излагать тот же самый вопрос.
Более естественный способ описать множество B состоит в том, чтобы
ослабить строгое разделение между молодыми и не молодыми. Мы будем
делать это, допуская не только (четкое) решение ДА он/она находится в
множестве молодых, или НЕТ он/она не в множестве молодых, но более гибких
фраз подобно Хорошо, он/она принадлежит немного больше к множеству
молодых или НЕТ, он/она почти не принадлежит к множеству молодых.
Как упомянуто во введении, мы хотим использовать нечеткие множества,
чтобы делать компьютеры более интеллектуальными. Теперь мы должны
закодировать вышеупомянутую идею более формально. В нашем первом
примере мы кодировали все элементы Области Исследования 0 или 1. Прямой
путь обобщить эту концепцию состоит в том, чтобы позволить большее
количество значений между 0 и 1. Фактически, мы даже позволяем бесконечно
многие варианты между 0 и 1, а именно единичный интервал I = [0, 1].
Интерпретация чисел, теперь назначенная всем элементам Области
Исследования, намного более трудная. Конечно, снова число 1 назначено
элементу как способ определить элемент который находится в множестве B и 0
- способ, при котором элемент не определен в множестве B. Все другие
значения означают постепенную принадлежность к множеству B.
Для большей наглядности, теперь мы показываем множество молодых,
подобно нашему первому примеру, графически при помощи символической
функции.
6
При таком способе 25-летние люди будут все еще молоды на 50 процентов.
Теперь Вы знаете, что такое нечеткое множество. Но что Вы можете делать с
этим?
Операции над нечеткими множествами
Теперь, когда мы имеем понятие, что такое нечеткие множества, мы можем
вводить основные операции на нечетких множествах. Подобно операциям на
четких множествах, мы также хотим определить пересечение, объединение и
отрицание на нечетких множествах. В ранней статье о нечетких множествах
Заде предложил оператор минимума для пересечения и оператор максимума
для объединения двух нечетких множеств. Легко видеть, что эти операторы
совпадают с четким объединением, и пересечением, если мы рассматриваем
только принадлежность к 0 и 1.
Чтобы разъяснять это, мы дадим несколько примеров. Допустим А есть
нечеткий интервал между 5 и 8, а B - нечеткое число, приблизительно 4.
Соответствующие диаграммы показаны ниже.
Следующая диаграмма показывает нечеткое множество между 5 и 8 И
(AND - пересечение) приблизительно 4 (синяя линия).
7
Нечеткое множество между 5 и 8 ИЛИ (OR-объединение) приблизительно
4 показывается в следующей диаграмме (снова, синей линией).
Следующая диаграмма является примером отрицания. Синяя линия ОТРИЦАНИЕ нечеткого множества A.
Нечеткое управление
Нечеткие контроллеры - наиболее важное приложение нечеткой теории. Их
работа сильно отличается от работы стандартных контроллеров; экспертное
знание используется вместо дифференциально-разностных уравнений, чтобы
описать систему. Это знание может быть выражено естественным способом,
использующим лингвистические переменные, которые описаны размытыми
множествами.
8
Применения Нечеткой Логики
Разделим возможную область применения Нечеткого Управления на две
группы.
Случаи, когда использование Нечеткого Управления разумно:

Для очень комплексных процессов, когда нет простой математической
модели

Для очень нелинейных процессов

Когда
необходимо
выполнить
обработку
(лингвистически
сформулированного) экспертного знания
Случаи, в которых использование Нечеткого Управления нерационально:

Стандартная
теория
управления
обеспечивает
удовлетворяющий
результат

Легко разрешимая и адекватная математическая модель уже существует

Задача не разрешима
9
МОДЕЛИРОВАНИЕ ЗАДАЧИ РАЗГОНА ОРУДИЯ НА ТРАКТОРЕ
«БЕЛАРУС»
Стояла задача создания модели разгона орудуя на тракторе «Беларус» с
использованием различных видов контроллеров, в том числе с использованием
«нечеткого» контроллера. Основными критериями качества управления были:
время разгона орудия (не более двух секунд) и обеспечение минимального
выброса момента после разгона.
На представленных ниже результатах работы контроллеров изображены:
на первом графике обороты двигателя и орудия; на втором – ускорение
буксования (заданное и реальное); на третьем – момент; на четвертом –
давление между фрикционными муфтами.
Результаты работы пропорционального регулятора:
10
Результаты работы пропорционального регулятора с инерционным звеном:
Результаты работы пропорционально-интегрального регулятора:
11
Результаты работы
инерционным звеном:
Результаты
работы
пропорционально-интегрального
регулятора
с
пропорционально-интегрально-дифференциального
регулятора:
12
Результаты работы нечеткого контроллера:
Результаты работы нечеткого контроллера с учетом скачка гистерезиса:
13
Наилучшие
результаты
были
получены
при
использовании
пропорционально-интегрального регулятора и нечеткого контроллера с учетом
скачка гистерезиса (наименьший выброс момента после разгона орудия).
Для построения нечеткого контроллера были выбраны следующие графики
функций принадлежности:
Для входной переменной
Для выходной переменной
База правил имеет следующий вид:
Если
отклонение
реального
ускорения
буксования
от
заданного
положительная величина, то изменение %ШИМ отрицательное;
Если отклонение реального ускорения буксования от заданного величина
близкая к нулю, то изменение %ШИМ близкое к нулю;
Если
отклонение
реального
ускорения
буксования
от
заданного
отрицательная величина, то изменение %ШИМ положительное;
14
СТРУКТУРА НЕЧЕТКОГО КОНТРОЛЛЕРА
При проектировании структурной схемы основное внимание было
уделено
созданию
универсального
нечеткого
контроллера.
Основными
факторами универсальности и гибкости контроллера являются:
- возможность изменения количества входных переменных;
- возможность изменения количества выходных переменных;
- масштабирования входного и выходного сигнала.
Первые два фактора обеспечиваются наличием отдельного блока для
вычисления функций каждой входной переменной и возможность наращивания
при необходимости входов и выходов блока активизации правил и блока
фаззификации.
Последний
фактор
обеспечивается
внесением
в
схему
блока
масштабирования.
Общая структурная схема нечеткого контроллера представлена на рис. 1.
15
X1
MB
F
RB
AB
Y1
FB
.
.
.
.
.
.
MB
Xn
MB
F
MB
[P]
Ym
[F]
MP
MP
рис. 1 Общая структурная схема
16
Общая структурная схема нечеткого контроллера.
В ее состав входят следующие блоки:
1.MB - Блок масштабирования(позиционирует и уменьшает/увеличивает
сигнал). Предназначен для адаптированию входных и выходных сигналов к
нужному диапазону значений. Коэффициенты масштабирования задаются для
каждого блока масштабирования отдельно. Данный блок делает систему более
универсальной.
2.F - Блок вычисления функций принадлежности(вычисляет по
входному значению значение функции принадлежности). Данный блок
предназначен для вычисления первой фазы нечеткого вывода.
3.RB
-
Блок
реализации
правил(активизирует
соответствующие
выходные правила). Данный блок на основании правил и полученных данных
от блока вычисления функций активизирует соответствующие выходные
правила.
4.AB - Блок объединения площадей. Данный блок объединяет площади
функции принадлежности выходных переменных в соответствии с правилами.
5.FB - Блок генерации выходных сигналов(генерирует результат в
зависимости от метода дефаззификации).
X[1..n], Y[1..m] – входной/выходной вектор.
MP[] – вектор коэффициентов масштабирования.
P[] – вектор правил.
F – тип функции, вычисляющей выходной вектор.
17
X
mul
sum
shift
sub
SS
KOEF
Y
div
MD
KOEF
LR
SHIFT
рис.2 Блок масштабирования
18
На рис.2 представлена структурная схема блока масштабирования, в ее
состав входят блоки математических функций для получения из исходного
сигнала сигнал, приемлемый для обработки на последующем шаге.
Блок
sum
представляет
собой
сумматор(SS
–
сигнал
выбора
сумматора/вычитателя, KOEF – коэффициент сложения/вычиния). Блок sub
представляет собой вычитатель. Блок mul представляет собой умножитель. (MD
–
сигнал
выбора
умножителя/делителя,
KOEF
–
коэффициент
умножения/деления) Блок div представляет собой делитель. Блок shift
представляет собой блок сдвига. X, Y – входной/выходной сигнал.
19
min
max
MUX
algp
TYPE
DC
Y
MUX
MUX
algs
MUX
drastp
TYPE
drasts
A B S/M
S/M
рис.3 Блок реализации правил
20
Блок реализации правил.
На рис.3 представлен блок реализации правил, который в зависимости
от входных параметров вычисляет степень истинности условий по каждому из
правил системы нечеткого вывода.
Сигнал S/M выбирает тип операции над подусловиями правила («И»
или «ИЛИ»). Блок DC представляет собой декодер реализации выбранной
операции, которую необходимо выполнить с подусловиями правила, т.к. в
нечетком выводе возможны различные варианты выполнения операций «И»,
«ИЛИ».С
помощью
мультиплексоров
на
выход
выводится
результат
вычисления необходимой функции. Функции в блоках min, max, algp, algps,
drastp, drasts реализуют различные виды операций и/или в рамках нечеткой
логики.
Следующий код демонстрирует реализацию данного блока на vhdl:
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.STD_LOGIC_ARITH.ALL;
use IEEE.STD_LOGIC_UNSIGNED.ALL;
-- Uncomment the following lines to use the declarations that are
-- provided for instantiating Xilinx primitive components.
--library UNISIM;
--use UNISIM.VComponents.all;
entity ruleblock is
port(
--tup: in std_logic_vector(1 downto 0);
mul: in std_logic;
clk : in std_logic;
code: in std_logic_vector(1 downto 0);
a,b : in integer;
y : out integer
);
end ruleblock;
architecture Behavioral of ruleblock is
component ttrig is
port(
input: in std_logic;
output: out std_logic
);
end component;
component mux21 is
21
port(
en : in std_logic;
clk: in std_logic;
a,b: in integer;
y: out integer
);
end component;
component algproizv is
port(
clk : in std_logic;
a,b: in integer;
mul, en : in std_logic;
y: out integer
);
end component;
component algsumm is
port(
clk : in std_logic;
a,b: in integer;
mul, en : in std_logic;
y: out integer
);
end component;
component drastproiz is
port(
clk : in std_logic;
a,b: in integer;
mul, en : in std_logic;
y: out integer
);
end component;
component drastsumm is
port(
clk : in std_logic;
a,b: in integer;
mul, en : in std_logic;
y: out integer
);
end component;
component granproiz is
port(
clk : in std_logic;
a,b: in integer;
mul, en : in std_logic;
y: out integer
);
end component;
component gransumm is
port(
clk : in std_logic;
a,b: in integer;
mul, en : in std_logic;
y: out integer
);
22
end component;
component max is
port(
clk : in std_logic;
a,b: in integer;
mul, en : in std_logic;
y: out integer
);
end component;
component min is
port(
clk : in std_logic;
a,b: in integer;
mul, en : in std_logic;
y: out integer
);
end component;
component mux4 is
port(
clk : in std_logic;
input0,input1,input2,input3 : in integer;
sel : in std_logic_vector(1 downto 0);
output : out integer
);
end component;
component decoder2
port(
code : in std_logic_vector(1 downto 0);
clk : in std_logic;
encode : out std_logic_vector(3 downto 0)
);
end component;
signal encode : std_logic_vector(3 downto 0);
signal y1,y2,y3,y4,y5,y6,y7,y8: integer;
signal yy1,yy2,yy3,yy4: integer;
signal clk2: std_logic;
begin
decoder21 : decoder2
port map(code=>code,clk=>clk,encode=>encode);
clk21 : ttrig
port map(input=>clk, output=>clk2);
min1 : min
port map(clk=>clk,a=>a,b=>b,mul=>mul,en=>encode(0),y=>y1);
max1 : max
port map(clk=>clk,a=>a,b=>b,mul=>mul,en=>encode(0),y=>y2);
algpro :
algproizv
port map(clk=>clk,a=>a,b=>b,mul=>mul,en=>encode(1),y=>y3);
algs : algsumm
port map(clk=>clk,a=>a,b=>b,mul=>mul,en=>encode(1),y=>y4);
granp : granproiz
port map(clk=>clk,a=>a,b=>b,mul=>mul,en=>encode(2),y=>y5);
grans : gransumm
port map(clk=>clk,a=>a,b=>b,mul=>mul,en=>encode(2),y=>y6);
23
drastp : drastproiz
port map(clk=>clk,a=>a,b=>b,mul=>mul,en=>encode(3),y=>y7);
drasts : drastsumm
port map(clk=>clk,a=>a,b=>b,mul=>mul,en=>encode(3),y=>y8);
mux1: mux21
port map(en=>mul,clk=>clk2,a=>y1,b=>y2,y=>yy1);
mux2: mux21
port map(en=>mul,clk=>clk2,a=>y3,b=>y4,y=>yy2);
mux3: mux21
port map(en=>mul,clk=>clk2,a=>y5,b=>y6,y=>yy3);
mux41: mux21
port map(en=>mul,clk=>clk2,a=>y7,b=>y8,y=>yy4);
mux5 : mux4
port map(clk=>clk,input0=>yy1,input1=>yy2,input2=>yy3,input3=>yy4,sel=>code,output=>y );
end Behavioral;
24
Блок вычисления значения функции принадлежности
Вариант 1
Вариант 2
0
1
зн1
зн2
...
...
999
зн1000
input
Decoder
output
Multiplexer
S1
D1
S2
D8
S
D
1
.
.
.
S3
ENB
S8
C1
C2
C3
ENB
type
[P]
type
рис.4 Блок вычисления значения функции принадлежности
25
Блок вычисления функций принадлежности.
На рис.4 представлен блок вычисления функций принадлежности,
который в зависимости от входных параметров вычисляет значение функции
принадлежности заданного вида. input, output – входное/выходное значение.
type – тип функции принадлежности. P – различные коэффициенты функций
принадлежностию. Реализация данного блока возможна в двух вариантах:
1.
При использовании для каждой функции своей аппаратной схемы
взависимости от типа функции. Недостатком такого подхода является
сложность схемы и разное время вычисления для разных типов
функции. Преимуществом является малые аппаратные затраты.
2.
При использовании табличного метода. В этом случае используется
ПЗУ, адрес в котором – входной аргумент функции, а значение по этому
адресу – выходное значение функции. Преимуществом является
простота реализации, скорость выполнения и одинаковое время
вычисления для разных типов функции. Недостатком является большие
аппаратные затраты.
26
ЗАКЛЮЧЕНИЕ
В данной работе была разработана структурная схема и реализация на
vhdl отдельных фрагментов нечеткого контроллера. Так же было проведено
программное моделирование системы средствами matlab. Была сделана
попытка создать наиболее универсальную структуру нечеткого контроллера
для обеспечения гибкости и расширения круга решаемых задач.
В перспективе планируется полная реализация контроллера на vhdl,
тестирование и внедрение.
27
ЛИТЕРАТУРА
1.
Алиев Р.А., Абдикеев Н.М., Шахназаров М.М. Производственные
системы с искусственным интеллектом.- М: Радио и связь. 1990. - 264 с.
2.
Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в
нечетких условиях. Тюмень: Изд-во Тюменского государственного
университета, 2000. - 352 с.
3.
Архангельский В.И., Богаенко И.Н., Грабовский Г.Г., Рюмшин Н.А.
Системы фуцци-управления. – К.: Тэхника, 1997. – 208 с.
4.
Беллман Р., Заде Л. Принятие решений в расплывчатых условиях.- В кн.:
Вопросы анализа и процедуры принятия решений.- М.:Мир, 1976. - С. 172-215.
5.
Берштейн Л.С., Боженюк А.В. Нечеткие модели принятия решений:
дедукция, индукция, аналогия. Таганрог: Изд-во ТРТУ, 2001. - 110 с.
28