Валы
реклама
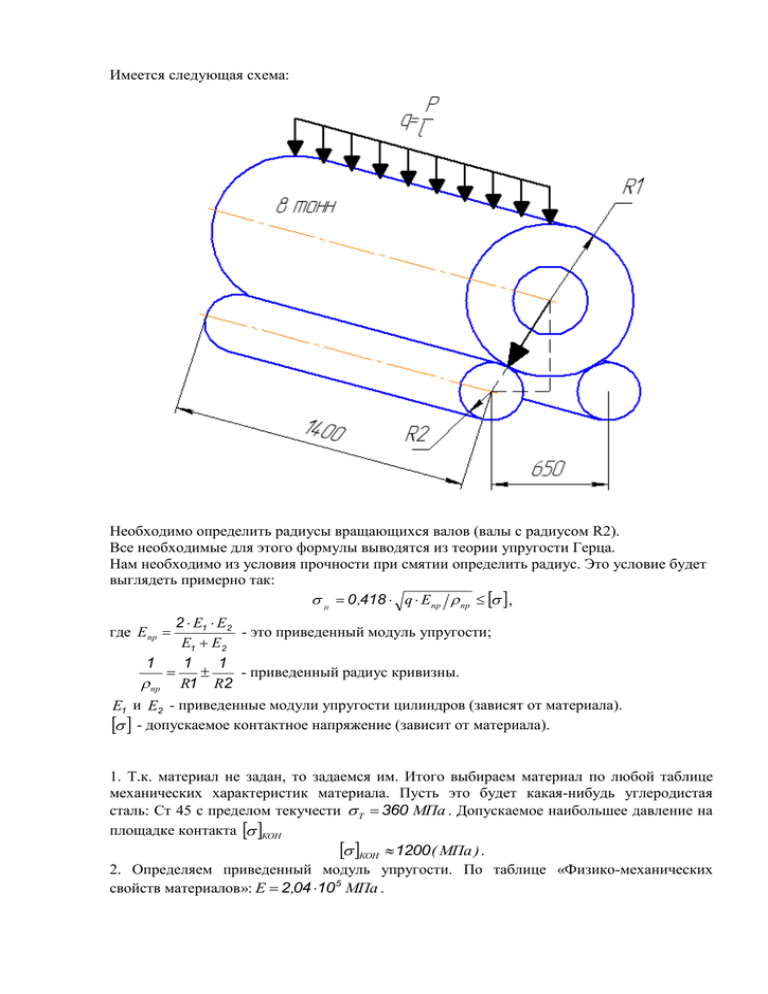
Имеется следующая схема: Необходимо определить радиусы вращающихся валов (валы с радиусом R2). Все необходимые для этого формулы выводятся из теории упругости Герца. Нам необходимо из условия прочности при смятии определить радиус. Это условие будет выглядеть примерно так: H 0 ,418 q Eпр пр , 2 Е1 Е2 - это приведенный модуль упругости; Е1 Е2 1 1 1 - приведенный радиус кривизны. пр R1 R2 где Е пр E1 и E2 - приведенные модули упругости цилиндров (зависят от материала). - допускаемое контактное напряжение (зависит от материала). 1. Т.к. материал не задан, то задаемся им. Итого выбираем материал по любой таблице механических характеристик материала. Пусть это будет какая-нибудь углеродистая сталь: Ст 45 с пределом текучести T 360 МПа . Допускаемое наибольшее давление на площадке контакта КОН КОН 1200 ( МПа ) . 2. Определяем приведенный модуль упругости. По таблице «Физико-механических свойств материалов»: E 2 ,04 10 5 МПа . 3. Конструктивно определяем диаметр вала радиусом R1. При весе 8 тонн, длине Н l 1400 мм , и кольцевом сечении. Удельный вес для Ст 45: 7 ,81 10 4 3 . м Известно, что вес полный вес вала Q равен 8 тонн=8000 кг = 80000 Н. Полный вес можно найти и по другой формуле: Q l F , тогда площадь поперечного сечения: Q l F 80000 H 1,4 м 7,81 10 4 H F м3 80000 H F 0 ,732 м 2 0 ,732 10 6 мм H 1,4 м 7,81 10 3 м Имея площадь легко найти размеры кольцевого поперечного сечения. Для «кольца» площадь равна: 4 F D 2 d 2 D 2 4 4 1 2 0 ,785 D 2 (1 2 ) d D Теперь конструктивно задаваясь коэффициентом определяем размеры. 1 Пусть , тогда D 3 d . Следовательно 3 1 2 F 0 ,785 D 2 1 3 D F 0 ,732 10 6 мм 2 1024 мм 1 2 0 ,785 1 3 1 2 0 ,785 1 3 1024 342 мм . Следовательно, D 1024 мм , d 3 Отсюда R1=512 мм. Пересчитываем полный вес и площадь: 1 2 2 2 3 2 F 0 ,785 D (1 ) 0 ,785 1024 10 1 0 ,732 м 2 3 4 Q 1,4 7 ,82 10 0 ,732 80139 ,36 H 325 ' Угол arc tg 32 24 512 Тогда сила Q’, действующая на цилиндр по нормали: Q' Q cos 80139 ,36 cos( 32 ,41 ) 67660 H Для всех валов принимаем E 2 ,04 10 5 МПа и коэффициент Пуассона 0,3 . Тогда: 0 ,418 Q' E 1 n l пр 1 пр l n 0 ,418 Q' E 2 Следовательно, 2 1200 10 6 Па 1,4 м 2 1672 5 6 пр 0 ,418 67660 Н 2 ,04 10 10 Па 1 1 1 1 1 1672 1672 1672 1670 R1 R2 R2 R1 0 ,512 1 R1 6 10 4 м Согласно этим расчетам R1 должен быть больше 0.6 мм. Т.к. расчет на контактную выносливость не достаточен для определения диаметра вала, то проведем ещё дополнительный расчет на прочность при изгибе. Для этого составляем расчетную схему, находим наибольший момент, определяем реакции в опорах (радиальная составляющая для подшипника): Определяем реакции в опорах: M 1 0 R2 1,4 q 1,4 0 ,7 0 49 1,4 0 ,7 34 ,3 кН 1,4 R1 R2 34 ,3 кН Максимальный момент будет по середине вала: M MAX R1 0 ,7 q 0.7 0 ,35 12 ,005 кНм Подбираем размер поперечно сечения из условия прочности: M W X max R2 T 300 МПа ( nT - коэффициент запаса прочности. Для расчета принимиаем nT равным 1.2) Тогда M 12005 WX max 40 см 3 300 10 6 d3 WX 0 ,1 d 3 32 3 0 ,1 d 40 d 7 ,37 см Принимаем диаметр вала 8 см. Подбор подшипников Расчет сводится к расчету по динамической грузоподъемности. Он сводится к определению долговечности в миллионах оборотов вращающегося кольца или в часах. Т.к. подшипники не воспринимают осевых нагрузок, предварительно выбираем подшипники радиальные роликовые. Так как нагрузки на опоры большие выбираем серию диаметров 3. Тип 2304: Подшипник роликовый радиальный с короткими цилиндрическими роликами (ГОСТ 8328-75). Посадочное место под подшипник d 20 мм ; Сr 20 ,5 кН ; Соr 10 ,4 кН Значит для радиальных подшипников радиальных: C L10 r Pr m (долговечность в миллионах оборотов) 10 6 L10 , где n – в об/мин. L10 h 60 n По ГОСТ 18855-82 и рекомендациям ВНИИПП для определения Pr установлены следующие расчетные зависимости для роликовых радиальных подшипников: Pr Fr K K T . K - коэффициент безопасности. Исходя из того, что вес рулона довольно таки значительный, значит здесь могут иметь место значительные нагрузки. Это характерно для валков и прокатных станков. Поэтому принимаем коэффициент безопасности: K 2,3 . KT - температурный коэффициент – выбирается в зависимости от рабочей температуры подшипника: допустим рабочая температура t 125 C , тогда KT 1.0 . Fr R 34 ,3 кН . Pr Fr K K T 34 ,3 10 3 2 ,3 1 78890 Н . Проверяем выполнение условия: Pr 0 ,5 C r 78890 0 ,5 20500 Следовательно, подшипники не удовлетворяют требованиям. Тогда для выполнения условия выбираем подшипник, который обалдает большей грузоподъемностью. Берем Роликовые радиальные сферические двухрядные подшипники (ГОСТ 5721-75). Для выполнения условия Pr 0 ,5 Cr выбираем подшипник 3612 или 113612: d 60 мм ; D 130 мм ; Сr 196000 Н ; Соr 128000 Н . Тогда, Pr 0 ,5 C r 78890 0 ,5 196000 98000 Условие соблюдается, следовательно, теоретически подшипники использовать можно. С виду данная схема напоминает какой-нить прокат, поэтому делаем допущение, что частота вращения вала меньше 100 об/мин. Тогда за n принимаем 100 об/мин: m C 196000 L10 r P 78890 r 10 3 18 ,726 10 10 6 10 6 196000 3 L10 L10 h 3121 ч 25000 ч 60 n 60 100 78890 Следовательно, надежность подшипников 3612 недостаточна. Выбираем подшипник 3614 или 113614: Сr 270000 Н ; Соr 181000 Н . Тогда, 10 10 6 10 6 27000 3 L10 L10 h 10069 ч 25000 ч 60 n 60 100 78890 Выбираем подшипник 3617 или 113617: Сr 365000 Н ; Соr 270000 Н . Тогда, 10 10 6 10 6 365000 3 L10 h L10 60 100 78890 27505 ч 25000 ч 60 n Подшипники имеют достаточный запас надежности. Окончательно принимаем диаметр вала равный диаметру посадочных подшипников: d 85 мм , т.е. RMIN 42 ,5 мм . колец


