реклама

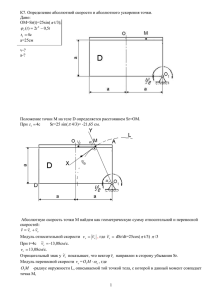
Примеры решения задач по кинематике Пример 1. Скорость материальной точки изменяется по закону м м 2 v 2t 3 i sin t j , где 1 4 , 1 с3, 1 . Определить с с 3 закон движения, если в начальный момент времени t=0 тело находилось в начале координат, т.е. r0 0,0,0 . Определить вектор ускорения. Решение. Закон движения r r t и вектор скорости v связаны дифференциальным уравнением dr dx dy dz v i j k. dt dt dt dt 2 t j запишем 3 В нашем случае из условия v 2t 3 i sin компоненты скорости v x , v y , v z 2 v x 2t 3 ; v y sin 3 t ; vz 0 . dx dy 2 2t 3 ; sin t ; dt dt 3 dz 0. dt По определению: vx dx ; dt vy dy ; dt vz dz . dt Разделим переменные и проинтегрируем dx 2t 3 dt ; 2 dy sin t dt . 3 3 dx 2t dt dt ; z c3 . Получим: 2 dy sin 3 t dt ; t4 t4 x t c1 t c1 ; 2 2 y 3 2 cos t c2 , 2 3 где с1, с2 – постоянные интегрирования, которые определяются из начальных условий. Учитывая, что х=0, y=0 при t=0 получаем, с1=0, c2 3 , с3=0. 2 Тогда закон движения материальной точки: t4 3 2 r t t i cos t 1 j . 2 2 3 Зная компоненты вектора скорости найдем компоненты вектора ускорения ax dv y dv x dv ; ay ; az z ; dt dt dt a x 6t 3 ; a y 2 2 cos t ; a z 0 ; 3 3 2 2 a 6t 3i cos t j . 3 3 Ответ: a 6t 3i Пример 2. Тело 2 2 cos t j 3 3 вращается вокруг неподвижной оси по закону 10 20t 2t 2 . Найти величину и направление полного ускорения точки, находящейся на расстоянии R = 0,1 м от оси вращения, для момента времени t = 4 с. Решение. Точка вращающегося тела описывает окружность. Полное ускорение точки: a an2 a2 ; a R ; an 2 R , где a , a n - тангенциальное и нормальное ускорение точки; - угловое ускорение; - угловая скорость. d 20 4t , dt d 4 . dt Согласно полученному выражению, угловое ускорение не зависит от времени, т.е. const . Тогда a 4 R 2 2 R 2 R 4 2 0,1 44 42 1,65 м . 2 с Из рис. 1.2 найдем направление полного ускорения cos an 1,6 0,97 , т.е. 140 . a 1,65 Ответ: 140 Пример 3.Два автомобиля, выехав одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного ими пути задается уравнениями S1 = At + Bt2 и S2 = Ct + Dt2 + Ft3. Определить относительную скорость автомобилей через 5 с, если A = 5 м/с, B = 6 м/с2, C = 1 м/с, D = 1 м/с2, F = 1 м/с3. Решение. Зная зависимость пройденного пути от времени, можно найти скорости первого и второго автомобиля: dS1 dS = A + 2Bt; 2 = 2 = С + 2Dt + 3Ft2. dt dt Для определения скорости первого автомобиля относительно второго (подвижная система отсчета) воспользуемся правилом сложения скоростей: 1 = 1 2 , где – скорость первого автомобиля относительно второго. Это векторное уравнение. Если ось координат направить по ходу движения автомобилей, то в проекции на эту ось получим: = 1 – 2; = A + 2Bt – C – 2Dt – 3Ft2; = (A – C) + 2(B – D)t – 3Ft2; = (5 – 1) + 2(6 – 1)5 – 3∙1∙25 = –21 м/с. Знак «минус» говорит о том, что первый автомобиль удаляется от второго назад со скоростью 21 м/с. Ответ: = –21 м/с. Пример 4. Движение материальной точки, перемещающейся по прямой, задано уравнением S = 4t3 + 2t + 1. В интервале времени от 1 до 2 с найти мгновенные скорости и ускорения в начале и конце интервала, среднюю скорость движения. Решение. Мгновенная скорость – первая производная от координаты по времени: = dS = 12t2 + 2. dt Скорости в начале и конце интервала равны: 1 = 12t12 + 2 = 12∙12 + 2 = 14 (м/с); 2 = 12t22 + 2 = 12∙22 + 2 = 50 (м/с). Ускорение – это первая производная от скорости по времени: a= d = 24t. dt В начале и конце интервала ускорения равны: а1 = 24t1 = 24 (м/с2); а2 = 24t2 = 48 (м/с2). Средняя скорость ‹ › движения точки определяется как отношение пути S, пройденного точкой за заданный интервал времени t, к этому интервалу: ‹ › = S S t2 S t1 = ; t t2 t1 3 3 4t23 2t2 1 4t13 2t1 1 4 t2 t1 2 ( t2 t1) ‹ › = = ; t2 t1 t2 t1 ‹ › = 4 23 1 2 (2 1) 2 1 = 30 м/с . Ответ: 1 = 14 м/с; 2 = 50 м/с; а1 = 24 м/с2; а2 = 48 м/с2; ‹ › = 30 м/с. Пример 5.С какой скоростью и по какому курсу должен лететь самолет, чтобы за 2 часа пролететь точно на север 720 км, если во время полета дует постоянный северо-западный ветер под углом 30º к меридиану со скоростью 36 км/ч? Решение. Скорость будем измерять в км/ч, как это делает летчик, определяя ее по приборам. Чтобы попасть в пункт назначения, самолету необходимо лететь под углом α к меридиану, отклоняясь на запад (см. рисунок). Обозначим искомую относительную скорость как , а результирующую абсолютную скорость, С направленную вдоль меридиана, как 0 . Ее модуль 0 З В S . t Из рисунка видно, что 0 u . Модуль вектора скорости треугольника косинусов: Ю найдем из векторного скоростей, используя теорему 02 u 2 20u cos 180 ; км2 км ; ≈ 392 км/ч. [] ч ч2 Таким образом, скорость полета самолета больше 0 . Угол можно найти по теореме синусов: u , откуда = 4,5º. sinα sin(180 β) Ответ: ≈ 392 км/ч; = 4,5º. Пример 6. Стрела пущена из лука вертикально вверх с начальной скоростью 0 = 40 м/с. Определить: 1) через какое время и с какой скоростью стрела упадет на землю; какой путь будет пройден ею за это время; 2) через какое время она окажется на высоте h = 35 м. Решение. В системе отсчета, связанной с Землей, ось ординат направим вертикально вверх, начало отсчета совместим с точкой бросания (см. рисунок). Считая, что движение стрелы прямолинейное и равнозамедленное, уравнения движения в проекциях на ось ОY будут иметь вид: gt 2 y = 0t – ; 2 (1) y = 0 – gt. (2) 1. В момент падения на землю t = tпол, y = 0. Из уравнения (1) найдем время полета: tпол = 20 2 40 ; tпол = = 8 с. g 9,8 Подставив tпол в уравнение (2), определим скорость падения стрелы: 20 – 0 . g Скорость падения равна по модулю начальной противоположна ей по направлению. y 0 – g скорости и В верхней точке траектории y = 0, из уравнения (2) найдем время подъема: tпод 0; g м с2 [tпод ] с. см Путь, пройденный стрелой за время движения, равен S = 2Ymax. Значение Ymax определим из уравнения (1), подставив в него tпод (время подъема). м 2 с2 02 02 402 Ymax = , тогда S = ; [S] = 2 = м; S = ≈ 160 м. 2g g 9,8 с м 2. Время подъема на высоту h определим, подставив в уравнение (1) значение y = h, тогда 35 = 40t – 5t2. Решая квадратное уравнение, получим t1 = 1 c; t2 = 7 c. Два значения для t указывают на то, что стрела на этой высоте побывает дважды: через 1 с (на подъеме) и через 7 с от начала движения (на спуске). Ответ: t = 8 с; S = 160 м; t1 = 1 c; t2 =7 с. Пример 7. На рисунке представлена зависимость ускорения а от времени t для материальной точки, движущейся прямолинейно. Определить скорость и координату х точки через t = 3 с после начала движения. В какой момент времени t1 точка изменит направление движения? Решение. Из графика следует, что зависимость ускорения от времени можно представить в виде a(t) = A – Bt, (1) где A = 4 м/с2; В = 2 м/с3. В случае прямолинейного движения скорость материальной точки при 0 = 0 (условие задачи) t adt . (2) 0 Подставив в формулу (2) выражение (1) и проинтегрировав, получим искомую скорость: Аt Bt 2 ; 2 м м с 2 м [] 2 c 3 ; с с с 43 29 12 – 9 3 м/с . 2 Искомая координата t t Bt 2 At 2 Bt 3 ; x dt At dt 2 2 6 0 0 м с 2 м с3 [ x] 3 м; с2 с x 4 9 2 27 18 9 9 м . 2 6 Точка изменяет направление движения в момент, когда скорость = 0, т.е. Bt 2 At 0, 2 откуда t 2А ; В м с3 [t ] 2 c; с м 24 t1 4 c. 2 Ответ: = 3 м/с; х = 9 м; t1 = 4 c. Пример 8. Тело брошено под углом к горизонту. Пренебрегая сопротивлением воздуха, определить этот угол, если максимальная высота подъема hmax меньше дальности полета S в n = 2,4 раза. Решение. Кинематические уравнения движения тела в векторной форме: gt 2 r r0 0t ; 0 gt ; а g , 2 где r0 – радиус-вектор, определяющий начальное положение тела в выбранной системе отсчета; 0 – начальная скорость тела; g – ускорение свободного падения. Направив оси координат (см. рисунок) из точки начала движения ( r0 = 0), получим уравнения движения в проекциях на оси Х и Y: x = 0xt ; x 0 x ; ax 0 ; (1) gt 2 y 0 yt ; y 0 y – gt ; a y g . 2 (2) Из рисунка следует, что 0 x 0 cos ; 0 y 0 sin . (3) Поскольку при у = hmax (в высшей точке траектории) у = 0, из второго соотношения (2) время подъема t1 0 y g . (4) Подставив формулу (4) в первое соотношение (2), найдем максимальную высоту подъема: hmax 02 y 2g . (5) В момент падения тела y(t) = 0, поэтому общее время движения из первого соотношения (2) t 20 y g . Из первого соотношения (1), используя формулу (4), дальность полета S 20 y 0 х g . (6) Разделив (5) на (6) и учитывая (3), найдем hmax tg . S 4 Согласно условию задачи hmax tg S , поэтому из выражения (7) n 4 4 1,66 , n 2,4 откуда искомый угол arctg1,66; 59 . Ответ: 59 . (7) Пример 9. Тело брошено вверх с высоты 12 м под углом 30º к горизонту с начальной скоростью 12 м/с. Определить продолжительность полета тела до точки А и до точки В (см. рисунок); максимальную высоту, которой достигает тело, дальность полета тела. Сопротивление воздуха не учитывать. Решение. В обозначенной на рисунке системе координат составляющие скорости х 0cos ; (1) y 0sin – gt . (2) Координаты тела с течением времени меняются в соответствии с уравнением равнопеременного движения: y H 0t sin x 0t cos . gt 2 ; 2 (3) (4) Время подъема тела найдем из условия, что в наивысшей точке подъема тела скорость у = 0. Тогда из уравнения (2) tподъема 0 sin . g (5) Время спуска тела от точки С до точки А равно времени подъема, поэтому продолжительность полета из точки О1 до точки А равна: t A 2tподъема 20 sin . g (6) Максимальную высоту подъема найдём из уравнения (3), подставив в него время подъема из уравнения (5): ymax H max 02 sin 2 . H 2g (7) Время полета до точки В найдем из уравнения (3), приравняв координату y к нулю (у = 0): 2 sin 2 H sin tB 0 0 . g g g (8) Дальность полета найдем из уравнения (4), подставив в него время движения из уравнения (8): xmax 0t B cos . Проведем вычисления по формуле (6): tA tA 20 sin ; g 2 12 0,5 1,22 с; 9,81 м с2 с; t A см по формуле (8): 2 sin 2 H sin tB 0 0 ; g g g 2 12 0,5 2 12 12 0,5 tB 2, 29 с; 9,81 9,81 9,81 2 м с2 м с2 м с2 с с с; t B см с м м по формуле (7): H max 02 sin 2 122 0,52 H 12 12 1,83 13,83 м; 2g 2 9,81 H max м м 2 с2 м м м; с2 м по формуле (9): xmax 0t B cos ; xmax 12 0,866 2,29 23,8 м; xmax м с м. с Ответ: tA = 1,22 с; t B = 2,29 с ; Hmax = 13,83 м ; xmax = 23,8 м. (9) Пример 10. По условию задачи 1.13 найти в момент приземления тела следующие величины: скорость и угол падения тела, тангенциальное и нормальное ускорение тела и радиус кривизны траектории. Решение. Результирующая или мгновенная скорость в точке В (см. рисунок) находится как векторная сумма составляющих х и у : В x y или В 02 cos 2 2y . Составляющую у в точке В найдем из уравнения (2) предыдущей задачи, подставив в него время движения tB из уравнения (8): у 0 sin – gt B (0 sin )2 2 gH . Тогда скорость в точке В В (0 cos )2 (0 sin )2 2 gH 02 2 gH ; В 122 2 9,81 12 19,48 м/с; В м2 м м м м 2 м/с. с с с2 с Для определения угла β, который составляет вектор скорости В с горизонтальной осью Х, воспользуемся треугольником скоростей (см. рис.) sin y B sin (0 sin )2 2 gH 02 2 gH ; 16,48 0,846; 19,48 arcsin0,846 5746. Построим в точке В треугольник ускорений. Тангенциальная составляющая ускорения 𝑎⃗τ направлена вдоль вектора мгновенной скорости в данной точке, т.е. по касательной к траектории. Нормальная составляющая ускорения 𝑎⃗𝑛 направлена перпендикулярно к вектору мгновенной скорости В . Их векторная сумма an a g . Тогда из рисунка находим: а g sin g y B ; а g sin 9,81 0,846 8,3 м/с2 . м м м aτ 2 мс 2 ; с с с аn g cos g x ; B аn gcos 9,81 0,533 5, 23 м/с 2 ; м м м an 2 мс 2 . с с с Радиус кривизны траектории в точке приземления определяем из уравнения 2B an , R откуда 2B 19,482 R 72,56 м ; an 5,23 м 2 с2 R 2 м. с м Ответ: В = 19,48 м/с; β = 57º46′; аτ = 8,3 м/с2; аn = 5,23 м/с2; R = 72,56 м. Пример 11. Материальная точка движется по закону r t A sin 5t i B cos 2 5t j , где А = 2 м, В = 3 м. Определить вектор скорости, вектор ускорения и траекторию движения точки. Решение. По условию задачи движение материальной точки задается изменением радиус-вектора с течением времени: r t x t i y t j z t k . (1) Сравнивая уравнение (1) с заданным, запишем движение точки координатным способом: x t Asin 5t ; 2 y t Bcos 5t ; z (t ) 0. Определим проекции вектора скорости на оси координат: dx х dt 5 А cos 5t ; dy 5 B 2cos 5t sin 5t 5 B sin 10t ; y dt dz z dt 0. Согласно выражению для мгновенной скорости (2) (3) dr x i y j z k dt выражение для вектора скорости будет иметь вид: t 5 A cos 5t i 5B sin 10t j . (4) Определим проекции вектора ускорения на координатные оси: d x a 25 A sin 5t ; x dt dy 50cos 10t ; a y dt d z a z dt 0. Согласно выражению для мгновенного ускорения d ax i a y j az k dt запишем выражение для вектора ускорения: a (5) a t 25 A sin 5t i 50 B cos 10t j . (6) Для определения траектории движения точки исключим из системы уравнений (2) время. Для этого представим систему в виде x sin 5t ; A cos 2 5t y . B (7) Возведя в квадрат левую и правую части первого уравнения в системе (7) и просуммировав уравнения, получим: x2 y sin 5t cos 5t 2 . B A 2 2 (8) Левая часть уравнения (8) равна 1, тогда x2 y 1. A2 B (9) Выражение (9) является уравнением параболы: A2 B Bx 2 . y A2 (10) Подставив в (10) данные из условия задачи, найдем траекторию движения точки: 3 y 3 x2. 4 Из полученного уравнения следует, что при у ≥ 0 траектория имеет вид параболы, расположенной выше оси х, по которой точка совершает колебательное движение. Ответ: t 10cos 5t i 15sin 10t j ; a t 50sin 5t i 150cos 10t j ; 3 y 3 x2 . 4 Пример 12. Радиус-вектор материальной точки, движущейся в поле м gt 2 j , где 0 76 ; g – тяготения Земли, описывается уравнением r 0ti с 2 ускорение свободного падения; i , j – орты координатных осей Х и Y. Определить момент времени t1 после начала движения, когда вектор скорости точки направлен под углом = 35º к горизонту. Чему равна скорость в этот момент времени? Решение. Согласно условию задачи gt 2 r 0ti j, 2 (1) откуда следует, что в начальный момент времени радиус-вектор r0 0 . Запишем, согласно уравнению (1), координаты точки (проекции радиусвектора): rx 0t; ry gt 2 . 2 При этом ось Y направлена вертикально вверх. Учитывая, что x dry drx , y , получаем: dt dt x 0 ; y gt , откуда следует, что здесь мы имеем дело с движением тела, брошенного горизонтально (см. рисунок). Из рисунка следует, что tg y x . С учетом формул (2) tg gt1 , откуда 0 искомый момент времени t1 t1 0 tg ; g м с2 с; см (2) t1 76 0,7 5,42 с . 9,8 Искомая скорость 2x 2y 0 1 tg 2 ; 76 1 0,7 92,8 2 Ответ: t1 5,42 с; 92, 8 м . с м . с Пример 13. Тело вращается вокруг неподвижной оси так, что его угловая скорость зависит от угла поворота φ по закону ω = ω0 – φ, где ω0 = 3 рад/с, = 0,1 с–1. В момент времени t0 = 0 угол φ0 = 0. Найти угловую скорость вращения тела для момента времени t = 2 c. Решение. Согласно определению угловая скорость d . dt Тогда по условию задачи d 0 – . (1) dt Разделим переменные в уравнении (1) и проинтегрируем полученное выражение: t d dt. 0 0 0 Пределы интегрирования берутся из условия задачи: 1 d (0 ) t dt ; 0 0 0 1 ln 0 t 0 t ; ln(0 – ) t ; 0 (2) ln 0 t. 0 (3) Потенцируем уравнение (3): 0 е – t . 0 (4) Из (4) находится выражение для угла поворота: 0 (1 е – t ). (5) Подставив (5) в заданный закон изменения угловой скорости, получим: 0е – t ; [ω] = рад/с; ω = 2,46 рад/с. Ответ: ω = 2,46 рад/с. Пример 14. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением ε = t, где = 0,02 рад/с3. Через какое время после начала вращения вектор полного ускорения произвольной точки тела будет составлять угол φ = 60º с ее вектором скорости? Решение. Разложим вектор полного ускорения а (см. рисунок) на составляющие а и аn . Тогда tg аn . а (1) Используя уравнение аτ = εR, запишем: а R tR . (2) С другой стороны, по определению а d . dt (3) Из уравнений (2) и (3) найдем: d . dt Разделим переменные в уравнении (4) и проинтегрируем его: tR (4) tRdt d ; t 0 0 tRdt d ; t2 R . (5) 2 Нормальное ускорение с учетом выражения (5) запишется в виде 2 2 Rt 4 . R 4 Подставим в формулу (1) уравнения (2) и (6): аn t 3 tg . 4 Из уравнения (7) найдем искомое время вращения тела: t3 4tg ; [t ] 3 c3 с; t3 Ответ: t = 7 с. 4 1,732 7 с. 0,02 (6) (7)