1.Введение в курс физики

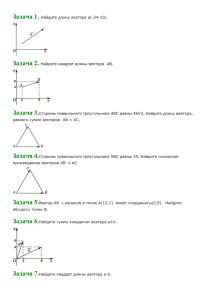
ВВЕДЕНИЕ
Физика – это основной раздел естественнонаучных знаний об
окружающем нас мире. Физика как наука занимается установлением и
описанием простейших (самых элементарных) взаимодействий в природе.
В то время такие естественнонаучные дисциплины, как химия, биология,
геология и др., используют более сложные взаимодействия в своих
исследованиях. Но только познав простейшие закономерности, можно
уверенно себя чувствовать в исследовании других разделов науки. Это все
и определяет физику как естественнонаучную основу знаний человечества.
Предлагаемое вниманию читателя учебное пособие предназначено для
самостоятельной активной подготовки старших школьников по физика.
Предполагается, что работая с данным пособием, читатель будет
пользоваться как основной (учебники физики средней школы), так и
дополнительной литературой по курсу элементарной физики, в которых
читатель найдет нужный теоретический материал.
Для лучшего усвоения материала желательно читать одни и те же
разделы не менее двух раз. При первом чтении следует познакомиться с
содержанием раздела, при повторном – выписывать основные положения,
а затем обязательно устно пересказывать прочитанный материал. В
каждом вопросе необходимо уметь выделить три момента:
1) вступление (с чего начинается ответ на вопрос);
2) главную или основную часть;
3) заключение (это прежде всего следствия и выводы, вытекающие из
главной части).
Для лучшего усвоения следует составлять конспект; при этом в него
следует записывать лишь самое главное: выводы формул, краткое и
лаконичное пояснение сущности физического явления или процесса,
формулировки
законов,
рисунки,
схемы,
подтверждающие
либо
иллюстрирующие изучаемый материал.
После усвоения теоретического материала учащийся может приступить
к решению задачи. Решение задач по физике – хорошее средство
применения теории на практике, причем, с одной стороны сам процесс
решения помогает более глубоко и сознательно овладеть изучаемым
материалом, с другой – знание теоретического материала – есть
непременное условие умения решать задачи.
Методические указания к каждой теме и примеры решения задач
данного пособия преследуют следующее:
1) пояснить применения изложенных методов;
2) углубить понимание физических законов;
3) развить умение рассуждать и сочетать знания из различных областей
знаний физики.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
Пытаясь понять и объяснить определенный класс явлений, ученые
часто прибегают
к использованию модели. При этом под моделью
понимается некоторый мысленный образ явления, опирающийся на уже
известные понятия и позволяющий построить полезную аналогию.
Например: а) материальная точка – всякое тело, обладающее массой,
размерами которого в данной задаче можно пренебречь или более точно –
математическая точка, обладающая массой; б) идеальный газ – это газ,
состоящий из молекул, которые являются материальными точками и не
обладают потенциальной энергией взаимодействия.
Ни одна модель не может быть безупречна, но может быть очень
полезной и часто приводит к важным теориям (например, постулаты Бора
для модели атома Резерфорда); однако не следует смешивать понятия
модели или теории с реальной системой или самими явлениями.
Закон – некоторые краткие, но достаточно общие утверждения
относительно
характера
явлений
природы,
которые
выдержали
экспериментальную проверку в широком классе наблюдаемых явлений.
Для количественного описания физических явлений необходимо ввести
понятие физических величин, которые количественно определяются в
сравнении с некоторыми однотипными величинами, условно принятыми за
единицу данной величины (например: 1 метр – это приблизительно
1/10000000 ¼ меридиана, проходящего через Париж, или более точно,
длина,
равная
1650763,73
длин
волн
в
вакууме
излучения,
соответствующего переходу между уровнями 2p10 и 5d3 атома криптона-86;
или Сименс – электрическая проводимость проводника сопротивлением в
1 Ом).
Из всего многообразия физических величин необходимо выбрать
некоторые (минимальное количество) в качестве основных, а все остальные
считать производными.
Сейчас в мировой практике наибольшее распространение получила
Международная система единиц физических величин – СИ.
Она содержит 7 основных физических величин: 1) длина (ед. измерения
метр), 2) время (секунда), 3) масса (килограмм), 4) сила тока (Ампер),
5)
температура (Кельвин), 6) количество вещества (моль), 7) сила света
(кандела). Все остальные физические величины определяются через
основные величины; например, скорость определяется как отношение
перемещения тела ко времени, за которое это перемещение произошло.
Основные величины по определению не могут быть выражены через другие
величины.
Когда мы говорим о размерности величины, мы имеем в виду основные
единицы, с помощью которых можно построить данную величину.
Размерность площади, например, всегда равна квадрату длины
(сокращенно [l2]; квадратные скобки здесь и далее обозначают
размерность); скорость (v) может измеряться в единицах км/ч, м/мин, м/с
и т.д., но размерность ее всегда равна размерности длины [l ], деленной на
размерность времени [t ], т.е. имеем [v ]= [l ]/[t ].
При
определении
размерности
величины
обычно
пользуются
размерностями основных, а не производных величин. Например, сила, как
мы увидим ниже, имеет размерность массы [m], умноженной на
ускорение [l / t2], т.е. ее размерность [m][l ]/[t2]. Решение любой задачи
по физике содержит и проверку размерности окончательной физической
величины. Проверка размерности позволяет избежать грубых ошибок,
поэтому прежде чем вычислять значение величины по полученной
формуле, необходимо вначале сделать проверку размерности. Допустим, в
результате решения мы получили некоторую расчетную формулу,
например:
t = v0/g + τ/2 + H / τg.
Поверка размерности этой формулы требует, чтобы все слагаемые были
выражены в одних и тех же единицах, только тогда их можно складывать,
т.е. [v0 ]/[ g ]= [τ ]=[H ]/[τ ][g ] и в самом деле, если [v ]=
м/с; [τ]=c; [Н]=м; [g]=м/с2; [Н/g τ]=м/((м/с2) с)=с и можно написать, что
[t]=с.
Все физические величины, изучаемые в элементарной физике можно
разделить на два класса: скалярные и векторы.
Скалярной физической величиной называется физическая величина,
для задания которой необходимо задать лишь число, например, время (t),
масса (m), температура (T) и др.
Векторной физической величиной называется физическая величина,
для задания которой необходимо задать число и направление действия этой
_
_
_
величины, например, ускорение (a), скорость (v), сила (F) и др. Векторные
величины обозначаются либо стрелочкой сверху над символом физической
величины, либо полужирным шрифтом.
Для правильного и быстрого понимания и описания некоторых
физических процессов необходимо уверенное владение векторной алгеброй.
Вспомним основные операции векторной алгебры.
1) Вектор полностью определяется заданием его длины (модулем) и
направлением. Направление обычно определяется углом между
вектором и осью либо между векторами.
Вектора могут быть свободными (т.е. допускают параллельный перенос в
любую точку пространства), скользящими (т.е. допускают скольжение вдоль
прямой, совпадающей с вектором), связанные (т.е. для них любые переносы
запрещены).
_
_
_
2) Умножение вектора (c) на скаляр (a). В этом случае вектор b=ac
_
_
будет сонаправлен с вектором c, а его модуль в a раз больше: а) c, a=
_
_
_
_
_
=3,5; b=ac б) c
,
a =-0,25; b=ac, т.е. умножение на (-1) меняет
направление вектора на противоположное.
3) Сложение векторов.
Существует два способа сложения векторов:
а) по правилу параллелограмма. В этом случае суммарный вектор равен
вектору,
совпадающему с
диагональю
_ _
параллелограмма,
a
a a+b
построенного на векторах
_ _
a и b из общего начала
b
b
(рис. 1). Еще один пример
показан на рис. 2.
Рис. 1
_
_
a
_
a
_
a+b
_
_
b
b
Рис. 2
_
б) по правилу треугольника. В этом случае от конца вектора a как от
_
начала откладывается вектор b, и тогда суммарный вектор – это вектор,
проведенный из начала первого вектора к концу второго вектора (рис.
3).
b
_
b
_ _
_
_
_
a
b
a
а
a+b
_
a
_
b
_ _
_ a+b
a
б
Рис. 3
Это правило позволяет проще, чем правило параллелограмма, получить
сумму трех и более векторов (см., например, рис. 4).
_
b
_
a
b
_
c
_
a
_
c
_
_
_
a+b+c
Рис. 4
4) Вычитание векторов, b - a . Действие вычитание можно заменить
_
_
действием сложения вектора b и вектора (-a).
5)Разложение вектора на составляющие.
_
Если заданы два неколлинеарных направления, то любой вектор d,
лежащий в одной плоскости с заданными направлениями, можно
представить единственным способом в виде суммы двух векторов:
_
_
_
_
_
d = d1 + d2, где векторы d1 и d2 коллинеарны с заданными
направлениями.
_
Для разложения вектора d необходимо через его начало провести
прямые параллельные заданным направлениям; затем проделать такую же
_
операцию для конца вектора d. В образовавшемся параллелограмме,
_
диагональю которого является вектор d, стороны этого параллелограмма
_
_
являются искомыми векторами d1 и d2.
_
Например, для разложения d по заданным направлениям ab и ce
_
построим a'b' ║ab и c'e' ║ce, затем через конец вектора d проводим
a"b" ║a'b' и c"e" ║c'e'. В образовавшемся параллелограмме стороны ОВ и
_
_
_
_
_
ОЕ являются искомыми векторами d1 и d2 , тогда d1+ d2 = d (рис. 5).
e'
e″ D
b″
a″
е
E
d1
d
с
B
a
b
a' O c'
Рис. 5
_
d2
c″
b'
6) Проекция вектора на ось.
Проекцией (ax) вектора на ось Х называется длина отрезка отсекаемого
_
на этой оси перпендикулярами проведенными через концы вектора a,
взятая со знаком плюс, если направление от проекции начала вектора на
ось к проекции его конца совпадает с положительным направлением оси, и
со знаком минус – в противоположном случае (рис. 6).
_
a
_
b
_
c
1
0
X
пр a=ax>0
bx=0
пр с=сx<0
_
(пр а)y = аy
Обозначим угол между вектором и осью ОХ через ; тогда проекцию
_
_
вектора a можно вычислить по формуле ax = |a|cos и соответственно
_
cx=|c|cos 1. Причем в этом случае соблюдается и правило знаков, т.е.
если <π/2, то cos >0, а если π/2< 1<π, то cos 1<0.
Совершенно очевидно, что если раскладывать вектора по двум
взаимоперпендикулярным направлениям, например, по осям Х и У
декартовой системы, то составляющие вектора по осям Х и У по модулю
совпадают с проекцией вектора на соответствующую ось (рис. 7).
Y
Поэтому принято записывать
_ _ _
это следующим образом: a=ax+ay,
_
_
где вектора ax и ay составляющие
_
_
_
a1
a
вектора a.
a2
Однако этой же записи можно
придать и другой вид, если ввести
понятие единичного вектора вдоль
оси.
Единичным вектором (ортом оси)
_
Называется
вектор
e,
направленный
в положительную
сторону оси, модуль которого равен
x
0
_
1, т.е. |e| = e =1.
_
(пр а)x = аx
Рис. 7
_
_
Орт оси ОХ обозначают ex, а орт оси
ОУ – ey.
_
Теперь составляющие вектора a по осям ОХ и ОУ можно записывать иным
_
_
_
_
способом: ax = axex; ay = ayey, где ax и ay - проекции вектора на
соответствующие оси. Следовательно, любой вектор можно всегда задать
через его проекции на оси декартовой системы координат, т.е. a (ax, ay).
_
Модуль вектора |a| через проекции по осям можно выразить по теореме
Пифагора, т.е.
_
__________
|a|= √ax2 + ay2
7) Скалярное произведение двух векторов.
_ _
Скалярным произведением a•b двух векторов
произведение их модулей
на косинус угла между
ними (рис. 8):
_
_
a и b называется
__
_
_
__
a•b = |a|•|b|cos(a, b)=
= a•b•
Скалярное произведение
может быть записано через
произведения этих векторов
на оси прямоугольной системы
координат:
_ _
_
_
_
_
a•b= (axex + ayey) • (bxex + byey)=
=axbx + ayby
_
a

=(a, b)
_
b
Доказательство этого соотношения
проведите самостоятельно, предварительно рассмотрев скалярное
_ _
_ _
произведение единичных векторов exex и exey.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
_
_
_ _
1. Даны два вектора a и b. Найти сумму a + b этих векторов. Модули этих
_
_
_
_
a
b
векторов равны |a| = 5 и |b| = 4.
2. Вдоль прямой АВ навстречу друг другу направлены два равных по
модулю вектора. Определить сумму и разность этих векторов.
3. В координатах Х и У задано положение точки М: х = 5; у = 5. Определить
_
модуль вектора r, соединяющего начала координат и точку М, а также
угол между этим вектором и осью Х.
_
_
(Ответ: |r| =7,1; =45˚).
4. Вектор a, модуль которого равен 4,0, составляет угол =240˚ с вектором
_
_
_
_
b, модуль которого равен 6,0. Определить модуль вектора c = a - b и
_
_
угол β между a и c.
_
_
(Ответ: |c| =8,7; β =37˚)
5. Вектор r, модуль которого равен 6,0, направлен под углом 30˚ к оси Х.
Определить проекции этого вектора на координатные оси Х и У.
6. Даны точки М1 (2; 10) и М2 (5;6). Определить модуль суммарного вектора
__
__
ОМ1 + ОМ2.
7. Разложить векторы на составляющие по заданным направлениям.
а)
б)
_
_
в)
_
_
8. Даны два вектора a и b, модули которых |a| =2; |b| =1. Угол между
ними = 60˚. Найти скалярное произведение этих векторов.
_ _
(Ответ: a•b =1).
_
_
9. Два вектора a и b заданы через свои компоненты ax = 3, ay = 4, bx = 7,
by = 1. Найти скалярное произведение этих векторов и угол между ними.
_ _
(Ответ: a•b =25; = 45˚).
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по теме «Введение в курс физики»
для абитуриентов физического
факультета