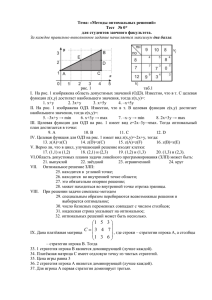
Методы оптимальных решений.

Г. Н. Камышова, Н. Н. Терехова
МЕТОДЫ ОПТИМАЛЬНЫХ
РЕШЕНИЙ
Краткий курс лекций
Саратов 2012
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ
УНИВЕРСИТЕТ имени Н.И.ВАВИЛОВА»
_____________________________________________________
Г. Н. Камышова, Н. Н. Терехова
МЕТОДЫ ОПТИМАЛЬНЫХ
РЕШЕНИЙ
Краткий курс лекций
Саратов 2012
1
УДК 517(075.8)
ББК 22.161.
К18
Издание осуществлено при поддержке
программы TEMPUS JP, грант Европейской
Комиссии 159188-TEMPUS-1-2009-1-PLTEMPUS-JPCR
Камышова Г. Н., Терехова Н. Н. Методы оптимальных решений.
(краткий курс лекций): Учебное пособие /сост.: Камышова Г. Н.,
Терехова Н. Н. – Саратов: Изд – во ФГБОУ ВПО «Саратовский ГАУ».,
2012.- 86 с.
ISBN
Краткий курс лекций подготовлен в соответствии с положениями
и требованиями Государственного образовательного стандарта
высшего профессионального образования, включает основные
теоретические вопросы, литературу по изучению курса.
Предназначено для студентов направления подготовки
110100.62 Агрохимия и агропочвоведение (профиль Агроэкология),
280100.68
«Природообустройство
и
водопользование»,
для
бакалавров направления “Экономика предприятий и организаций”
профиль“ Экономика предприятий и организаций (агропромышленного
комплекса)”,
“Бухгалтерский
учёт
и
аудит”,
“Пищевая
промышленность”, “Финансы и кредит”, а также для магистров,
аспирантов, преподавателей, научных сотрудников.
Данный материал опубликован при поддержке Европейского
Союза. Содержание публикации является предметом ответственности
авторов и не отражает точку зрения Европейского Союза.
ISBN
© Камышова Г. Н., Терехова Н. Н.,
2012
© ФГБОУ ВПО СГАУ имени
Н.И. Вавилова, 2012
2
ВВЕДЕНИЕ
В курсе рассматриваются вопросы, связанные с построением
математических моделей ситуаций целенаправленного принятия решения,
исследуются свойства этих моделей, излагаются методы и алгоритмы,
позволяющие находить оптимальные значения отвечающих за рациональный
выбор параметров. Значительное внимание уделяется ситуациям, в которых
при формировании оптимального решения необходимо учитывать интересы
различных сторон.
Краткий курс лекций имеет прикладную направленность:
теоретический материал иллюстрируется достаточно доступными примерами
и задачами, имеющими, как правило, экономический и социальный характер.
Материал
данного
курса
найдёт
свое
конкретное
применение
в
общепрофессиональных и специальных дисциплинах факультета экономики,
посвященных микро- и макроэкономике, государственному управлению и
экономике общественного сектора, фондовому рынку и финансовому
менеджменту, институциональной экономике и ряду других научных
областей. Поэтому данный курс лекций является важной составляющей
системы фундаментальной подготовки современного экономиста, а также
обеспечивает ему профессиональную мобильность.
3
ЛЕКЦИЯ 1
Исследование операций. Экономико-математические модели.
Управление организационными системами (оргсистемами) – сложная
проблема. Характерной особенностью таких систем является включение в
них,
наряду
с
материальными,
информационными
ресурсами,
денежными,
также
и
энергетическими
коллективов
и
людей,
взаимодействующих как между собой, так и с указанными ресурсами.
Примерами оргсистем служат фирмы, ведомства, министерства, вузы и их
филиалы, города и др.
Оргсистемы являются объектом изучения теории исследования
операций.
Под операцией понимают совокупность действий, направленных на
достижение поставленной цели.
Исследование операций – научная дисциплина, занимающаяся
разработкой и практическим применением методов управления различными
оргсистемами.
Ее цель – количественное обоснование принимаемых управленческих
решений и прогнозных планов развития.
Исследование операций осуществляется на математических моделях
изучаемых объектов.
Термин «модель» используется в различных сферах человеческой
деятельности и имеет множество смысловых значений. В нашем курсе
лекций определим модель как материальный или мысленно представляемый
объект, который в процессе исследования замещает объект-оригинал так, что
его непосредственное изучение дает новые знания об объекте-оригинале.
Следовательно, модель является инструментом научного познания. Она
строится субъектом исследования так, чтобы отобразить характеристики
объекта-оригинала (свойства, взаимосвязи, структурные и функциональные
параметры и т.п.), существенные для цели исследования. Поэтому вопрос об
4
адекватности
модели
объекту-оригиналу
правомерно
решать
лишь
относительно определенной цели.
Процесс построения, изучения и применения моделей называется
моделированием. Его сущность схематически представлена на рис. 1.
Этап I
Объект
исследования
Этап IV
Модель
построение модели
проверка и
применение
знаний
Знания
об объектеоригинале
изучение
модели
Этап II
Этап III
Знания
о модели
перенос знаний
с модели на оригинал
Рис. 1.
Моделирование в экономике – это воспроизведение экономических
объектов и процессов в ограниченных, малых, экспериментальных формах, в
искусственно созданных условиях.
В
экономике
моделирование
в
основном
посредством
используется
описания
математическое
экономических
процессов
математическими зависимостями. При изучении экономических процессов
математические модели рассматриваются в тесной связи с целевыми
системами
называемые
и
представляют
собой
некоторые
экономико-математическими
целостные
моделями
структуры,
(ЭММ).
Таким
образом, ЭММ – модели, включающие в себя совокупность математических
зависимостей, логических построений, схем, графиков и т.д., связанных в
некоторую единую систему, имеющую экономический смысл.
Приведем следующую общую классификацию ЭММ.
5
По целевому назначению ЭММ делятся на теоретико-аналитические и
прикладные.
Теоретико-аналитические
ЭММ
предназначены
для
исследования общих свойств и закономерностей экономических процессов.
Прикладные ЭММ используются при решении конкретных экономических
задач.
По характеру отражения причинно-следственных связей выделяют
жестко детерминистские ЭММ и ЭММ, учитывающие случайность и
неопределенность.
По способам отражения фактора времени ЭММ делятся на
статические и динамические. В статических ЭММ все зависимости относятся
к одному моменту или периоду времени. Динамические ЭММ характеризуют
изменения экономических процессов во времени.
По
исследуемым
экономическим
процессам
различают
макроэкономические и микроэкономические ЭММ. Макроэкономические
модели строятся на уровне национального хозяйства, а микроэкономические
– на уровне организаций, их объединений и отдельных регионов.
Существуют и другие признаки классификации ЭММ. Причем с
развитием
экономико-математических
исследований
классификация
исследуемых ЭММ расширяется.
Отметим также, что по характеру используемого математического
аппарата при построении ЭММ различают методы классической и
прикладной математики.
Методы классической математики включают математический анализ,
линейную алгебру, теорию вероятностей и др.
Методы прикладной математики включают линейное, нелинейное,
динамическое, целочисленное и другое программирование, математическую
статистику, комбинаторику, теорию игр, управление запасами, теорию
массового обслуживания, экспертные оценки и др.
Одним из признаков качества функционирования оргсистемы является
критерий оптимальности ее функционирования. В сфере принятия
6
экономических решений критерий оптимальности
– это показатель,
выражающий предельную меру экономического эффекта принимаемого
управленческого решения для сравнительной оценки возможных решений и
выбора наилучшего из них.
Критерий
оптимальности,
как
правило,
носит
количественный
характер. Например, в его роли могут выступить максимум прибыли или
минимум затрат.
Математической формой критерия оптимальности в ЭММ является так
называемая целевая функция, экстремальное значение которой характеризует
предельно
допустимую
эффективность
деятельности
моделируемого
объекта-оригинала.
На практике нередко успех операции оценивается не по одному, а сразу
по нескольким критериям. В этом случае для выбора оптимального решения
используют два подхода.
Первый подход заключается в том, что в целевой функции
устанавливают приоритет критериев введением специальных коэффициентов
(весов).
Второй подход состоит в отбрасывании из множества допустимых
решений заведомо неудачных решений, уступающих другим по всем
критериям. В результате такой процедуры остаются эффективные или так
называемые «паретовские» решения, множество которых существенно
меньше исходного.
Компромиссное решение – решение, оптимальное по всем критериям,
как правило, не существует. И потому окончательный выбор приемлемого по
этим критериям решения остается за лицом, принимающим решение.
7
ЛЕКЦИЯ 2
Балансовые модели. Модель Леонтьева многоотраслевой экономики.
Продуктивные модели.
В экономике существует баланс между отдельными отраслями.
Рассмотрим простой вариант модели межотраслевого баланса – модель
«затраты-выпуск».
Пусть
имеется
n
различных
отраслей,
каждая
из
которых
производит свой продукт и нуждается в продукции других отраслей
(производственное потребление). Введем следующие обозначения:
xi
- общий объем продукции отрасли i за плановый год - так
называемый валовой выпуск отрасли i;
xij - объем продукции отрасли i, расходуемый отраслью j в процессе
производства;
yi - объем продукции отрасли i, предназначенный к потреблению в
непроизводственной сфере - объем конечного потребления. В него входят
создаваемые
в
хозяйстве
обеспечение
общественных
запасы,
личное
потребностей
потребление
(просвещение,
граждан,
наука,
здравоохранение, развитие инфраструктуры и т.д.), поставки на экспорт.
Указанные величины сведем в таблицу.
Производственное
потребление
x11
x12

x1n
x 21
x 22 
x2n
...........
x n1
xn 2

x nn
Конечное
Потребление
y1
y2

yn
Валовой
выпуск
x1
x2

xn
Балансовый характер этой таблицы выражается в том, что при
любом i  1,, n выполняется соотношение
xi  xi1  x i 2    xin  y i , (1)
8
означающее,
что
производственное
валовой
потребление,
выпуск
равное
расходуется
на
xi1  xi 2    xin ,
и
xi
непроизводственное потребление, равное уi. Соотношения (1) называют
соотношениями баланса.
Единицы измерения всех указанных величин могут быть или
натуральными (кубометры, тонны, штуки и т. п.), или стоимостными. В
зависимости
от
этого
различают
натуральный
и
стоимостной
межотраслевой балансы. В дальнейшем будем иметь в виду стоимостной
баланс.
В. Леонтьев обратил внимание на важное обстоятельство: величины
aij 
xij
xj
остаются постоянными в течение ряда лет, что объясняется
примерным постоянством используемой технологии производства.
Сделаем следующее допущение: для выпуска любого объема xj
продукции отрасли j необходимо затратить продукцию отрасли i в
количестве aij x j , т.е. материальные издержки пропорциональны объему
производимой продукции:
xij  aij x j
Коэффициенты
a ij
i, j  1,, n. (2)
называют
коэффициентами
прямых
материальных затрат или коэффициентами материалоемкости. Они
показывают сколько необходимо единиц продукции отрасли
i для
производства единицы продукции отрасли j, если учитывать только прямые
затраты.
Подставив (2) в балансовое соотношения (1), получим
x1  a11 x1  a12 x 2    a1n x n  y1
x 2  a 21 x1  a 22 x 2    a 2 n x n  y 2
. . . . . . . . . . . . . . . . . . . .
x n  a n1 x1  a n 2 x 2    a nn x n  y n
9
или, в матричной записи,
x  Ax  y , (3)
где
 a11

 a 21
A  . . .

 a n1


a1n 

a 22  a 2 n1 
. . . . . . . . . ,

a n 2  a nn 


a12

 x1 
 
x 
x   2 ,

 
 xn 
 y1 
 
y 
y   2 .

 
 yn 
Вектор x называется вектором валового выпуска, вектор y - вектором
конечного потребления, а матрица А - матрицей прямых затрат.
Соотношение
(3)
называется
уравнением
линейного
межотраслевого
баланса. Вместе с изложенной интерпретацией матрицы А и векторов x и y
это соотношение называют также моделью Леонтьева.
Уравнения межотраслевого баланса можно использовать для плановых
расчетов:
- задавая для каждой отрасли i валовой выпуск продукции x i можно
определить объемы конечного потребления каждой отрасли y i :
y  E  Ax ,
где Е – единичная матрица;
- задавая величины конечного потребления каждой отрасли y i можно
определить величины валового выпуска продукции x i :
x   E  A y ,
1
где
E  A1
– матрица, обратная к матрице
 E  A ,
ее элементы
называют коэффициентами полных материальных затрат.
Отметим особенности системы (3): все компоненты матрицы А, а также
векторов x и y неотрицательны (это вытекает из экономического смысла А,
x и y ). Для краткости будем записывать это так: A  0, x  0,
10
y  0.
Таким образом, плановые расчеты по модели Леонтьева можно
выполнять при соблюдении следующего условия продуктивности:
матрица A  0 называется продуктивной, если для любого вектора
y  0 существует решение x  0 уравнения (3).
В этом случае и модель Леонтьева, определяемая матрицей А, тоже
называется продуктивной.
Сформулируем критерии продуктивности матрицы A  0 .
Критерий I. Матрица A  0 продуктивна тогда и только тогда, когда
матрица E  A1 существует и неотрицательна.
Критерий II. Матрица A  0 продуктивна тогда и только тогда,
когда имеет место разложение матрицы E  A
1
в матричный ряд
E  A1  E  A  A2  A3    An   . (4)
В соотношении (4) матрицы A2 , A3 , , An ,  называются матрицами
коэффициентов косвенных затрат 2-го, 3-го и т.д. порядков. Их сумма
образует матрицу коэффициентов косвенных затрат
B  A2  A3    An   .
(5)
Суть косвенных затрат поясним на примере производства двигателей.
На их изготовление в виде прямых затрат расходуется сталь, чугун и т.д. Но
для производства стали также нужен чугун. Следовательно, производство
двигателей включает как прямые, так и косвенные затраты чугуна.
Таким образом, из соотношений (4) и (5) имеем
E  A1  E  A  B ,
(6)
т.е. матрица коэффициентов полных материальных затрат включает в
себя матрицы коэффициентов прямых и косвенных затрат.
Рассмотрим примеры.
11
Пример 1. Исследовать на продуктивность матрицу
 0,05 0,45 0,4 


A   0,1 0,2 0,5 
 0,2 0,3 0,1 


Решение. Сначала найдем матрицу E  A :
 1 0 0   0,05 0,45 0,4   0,95  0,45  0,4 

 
 

E  A   0 1 0    0,1 0,2 0,5     0,1
0,8
 0,5 
 0 0 1   0,2 0,3 0,1    0,2  0,3
0,9 

 
 
Затем найдем
E  A1 .
С этой целью по известным из линейной
алгебры правилам вычислим определитель
0,95
detE  A   0,1
 0,2
 0,45  0,4
0,8
 0,3
0,95  0,45  0,4
 0,5   0,1
0,9
 0,5   0,1
0,8
 1,9
0
0,95  0,85  0,4
1,9
0,3
0
 0,5 
0
1,9
0,95  0,85
 1,9  0,285  0,085   0,38;
 0,1 0,3
алгебраические дополнения для элементов матрицы E  A
 1,9 
 111
0,8
 0,5
 112
 0,57 ;
 0,3 0,9
 0,1 0,8
 113
 0,19 ;
 0,2  0,3
0,95  0,4
 122
 0,775 ;
 0,2 0,9
 0,45  0,4
 131
 0,545 ;
0,8
 0,5
 0,1  0,5
 0,2 0,9
 0,4
21  0,45
 1
 123
 0,3
0,9
0,95  0,45
 0,2  0,3
 0,4
3 2 0,95
 1
12
 0,1  0,5
 0,1 ;
 0,525 ;
 0,375 ;
 0,515 ;
 133
0,95  0,45
 0,1
0,8
 0,805 .
Тогда
 E  A
1
 0,57 0,525 0,545 
 57 52,5 54,5 
 1

1 

 0,1 0,775 0,515    10 77,5 51,5 
0,38 
 38  19 37,5 80,5 
 0,19 0,375 0,805 


Полученная матрица неотрицательна и по Критерию I исходная
матрица А продуктивная.
Пример 2. Для матрицы А коэффициентов прямых затрат из примера 1
и вектора конечного потребления
152 


y  114 
190 


найти: а) вектор валового выпуска; б) матрицу косвенных затрат; в)
изменение вектора валового выпуска при увеличении вектора конечного
потребления на величину
 76 
 
y   38 
 38 
 
Решение.
а) Вектор валового выпуска x вычислим по формуле
x   E  A y .
1
Имеем
13
 57 52,5 54,5  152   57 52,5 54,5   4   658 

 
  

1
x   10 77,5 51,5  114    10 77,5 51,5   3    530 
38 

 
  

 19 37,5 80,5  190   19 37,5 80,5   5   591 
б) Матрицу косвенных затрат В найдем из соотношения (2.6):
 57 52,5

1
1
B  E  A  E  A   10 77,5
38 
 19 37,5
 17,1
1
  6,2
38 
11,4
в)
54,5   1 0 0   0,05 0,45 0,4 
 
 

51,5    0 1 0    0,1 0,2 0,5  
80,5   0 0 1   0,2 0,3 0,1 
35,4 39,3 

31,9 32,5 
26,1 38,7 
 57 52,5 54,5   76   221

  

1
1
x  E  A y   10 77,5 51,5   38   149 
38 
  

 19 37,5 80,5   38  156 
Таким образом, при увеличении вектора конечного потребления на
 221 
 76 


 
y   38  вектор валового выпуска увеличится на x  149  .
 38 
156 


 
14
ЛЕКЦИЯ 3,4,5
Задачи математического и линейного программирования.
Модели линейного программирования.
Нередко экономические задачи имеют не единственное решение и
требуется выбрать лучшее – оптимальное из них. Моделирование таких задач
сводится к задачам математического программирования (ЗМП).
Математическое программирование – область математики, изучающая
оптимизационные процессы посредством поиска экстремума функции при
заданных ограничениях.
Сформулируем в общем виде ЗМП:
f  x1 , x2 , , xn   max min 
(7)
при условиях
g1  x1 , x2 , , xn   bi , i  1, 2, , k , 

g1  x1 , x2 , , xn   bi , i  k  1, , l ,  (8)
g1  x1 , x2 , , xn   bi , i  l  1, , m,

x1  0, x2  0, , xn  0,
(9)
где f  x1 , x2 , , xn  – целевая функция, условия (8) – специальные
ограничения, условия (9) – общие ограничения ЗМП.
Точку
x1 , x2 , , xn  ,
координаты
которой
удовлетворяют
ограничениям (8) и (9), называют допустимым решением ЗМП.
Множество всех допустимых решений ЗМП называют допустимым
множеством.

*
*
*

Допустимое решение x1 , x2 , , xn , удовлетворяющее соотношению
(7), называют оптимальным решением ЗМП.
15
Если
в
ЗМП
целевая
функция
f  x1 , x2 , , xn 
и
функции
g1  x1 , x2 , , xn , i  1, 2, , m , – линейные, то имеем общую задачу
линейного программирования (ЗЛП):
c1 x1  c2 x2    cn xn  F  max min 
(10)
ai1 x1  ai 2 x2    ain xn  bi , i  1, 2, , k , 

ai1 x1  ai 2 x2    ain xn  bi , i  k  1, , l ,  (11)
ai1 x1  ai 2 x2    ain xn  bi , i  l  1, , m,

x1  0, x2  0, , xn  0,
(12)
В
зависимости
от
вида
специальных
ограничений
различают
следующие ЗЛП:
- каноническая ЗЛП, включающая в качестве ограничений (11) только
уравнения, т. е.
ai1 x1  ai 2 x2    ain xn  bi , i  1, 2, , m ;
- стандартная ЗЛП, включающая в качестве ограничений (11) только
неравенства, т. е.
ai1 x1  ai 2 x2    ain xn  bi , i  1, 2, , l ,
ai1 x1  ai 2 x2    ain xn  bi , i  l  1, , m.
Рассмотрим следующие примеры моделей, приводимых к ЗЛП.
Пример 1. Экономико-математическая модель задачи о планировании
производства.
На заводе имеются запасы трех видов сырья: S1 , S 2 и S 3 , из которого
можно наладить производство двух видов товаров: T1 и T2 . Запасы сырья,
норма его расхода на производство единицы товаров, а также прибыль от
реализации единицы каждого товара приведены в таблице 1 (цифры
условные).
16
Таблица 1
Сырье
Товары
T1
T2
Запасы
Прибыль
S1
S2
S3
3
1
1
25
3
126
2
48
4
72
34
Необходимо составить такой план производства товаров, при котором
прибыль от их реализации будет максимальной.
Решение.
План производства зададим числами x1 и x 2 , где x i – количество
единиц товара Ti , которое следует произвести i  1, 2  . Неизвестные x1 и
x 2 должны удовлетворять условиям
 3x1  3x2  126

или
 x1  2 x2  48
 x1  4 x2  72
x1  0, x2  0
 x1  x2  42

 x1  2 x2  48 , (13)
 x1  4 x2  72
(14)
Поясним смысл первого неравенства системы (13). В левой части
записано количество сырья S1 , которое расходуется на выпуск x1 единиц
товара T1 и x 2 единиц товара T2 . Это количество не должно превышать
имеющегося запаса сырья S1 , т. е. 126 единиц. Аналогичный смысл
имеют второе и третье неравенства системы (13).
Прибыль, предприятия от реализации плана ( x1 , x 2 ) производства
товаров, очевидно, составит
F  25 x1  34 x2 .
В
интересах
предприятия
(15)
максимизировать
эту
прибыль.
Следовательно, чтобы составить план производства товаров, при котором
прибыль от их реализации будет максимальной нужно решить стандартную
ЗЛП: F  25 x1  34 x2  max при условиях (13) и (14):
17
 x1  x2  42
 x  2 x  48
 1
2

 x1  4 x2  72
 x1  0, x2  0
Пример 2. Экономико-математическая модель задачи о диете.
Имеются два вида продуктов: P1 и P2 . Содержание в 1 кг питательных
веществ A, B и C, ежесуточные потребности организма V в них и стоимость S
1 кг продуктов приведены в таблице 2
Таблица 2
Витамины
Продукты
P1
P2
V
Составить
такую
A
B
C
S
1
3
1
8
3
6
1
9
8
8
16
ежесуточную
диету,
которая
обеспечивает
необходимое количество питательных веществ при минимальных затратах на
продукты.
Решение.
Пусть
x1
и
x2
– искомые количества продуктов
P1
и
P2
соответственно. Их стоимость составляет
f  8 x1  16 x2
Общее количество питательного вещества A в обоих видах продуктов
равно x1  3x2 . Оно должно быть не меньше 6 единиц: x1  3x2  6 .
Аналогичные неравенства составим для питательных веществ B и C:
3 x1  x2  9 и x1  8 x2  8 .
Очевидно, x1  0 и x2  0 .
Таким образом, получим следующую стандартную ЗЛП:
18
f  9 x1  12 x2  min
(16)
 x1  3 x2  6
3 x  x  9
1
2
x  8x  8
2
 1
 x1  0, x2  0
(17)
при условиях
Геометрический метод решения задач линейного
программирования.
Геометрический метод решения ЗЛП – простой и наглядный способ
решения стандартных ЗЛП с двумя переменными:
F  c1 x1  c2 x2  max min 
(18)
при условиях
ai1 x1  ai 2 x2  bi , i  1, , l ,


ai1 x1  ai 2 x2  bi , i  l  1, , m, (19)

x1  0, x2  0,

Рассмотрим следующие геометрические объекты.
Выпуклые множества и их свойства.
Множество
точек
называется
выпуклым,
если
оно
вместе
с
произвольными двумя своими точками содержит весь отрезок, соединяющий
эти точки.
Справедливо утверждение: пересечение любого числа выпуклых
множеств есть выпуклое множество.
Каждое
неравенство
системы
ограничений
(19)
геометрически
определяет полуплоскость с граничной прямой ai1 x1  ai 2 x2  bi , i  1, , m ,
или x1  0 , или x2  0 .
Поясним сказанное. Рассмотрим, например, неравенство 3x1  4 x2  12 .
19
Ï åðâ. ï ð
À2
B1
B2
À4
À2
Посмотрим прямую L: 3x1  4 x2  12 (см. рис.2).
B1
B2
À3
À1
À1
Ñï ðàâ. ¹
x2
3
L
0
x1
4
ÊÎÌÏÀÑ-3D LT (ñ) 1989-2007 ÇÀÎ ÀÑÊÎÍ, Ðîññèÿ. Âñå ïðàâà çàùèùåíû.
Èí â. ¹ ï î äë.
Ï î äï . è äàò à
Âçàì . èí â. ¹ Èí â. ¹ äóáë.
Ï î äï . è äàò à
Рис. 2
Для того чтобы определить, какая полуплоскость удовлетворяет
заданному неравенству, необходимо выбрать любую точку, не лежащую на

1<
2 <
3
F=
L, и подставить ее координаты в неравенство. Если неравенство будет
данная
точка
является
допустимым
2
решением, F=и

полуплоскость, содержащая точку, удовлетворяет неравенству. Как правило,1
Подставим x1  x2  0 в заданное неравенство: 3  0  4  0  12 . Получим


в качестве «пробной» берут точку O0; 0  .

то

выполняться,
истинное утверждение. Следовательно, заданному неравенству соответствует
нижняя полуплоскость (заштрихованная на рис. 2), содержащая точку
O0; 0  .
Полуплоскости,
описываемые
неравенствами
(19)
Èçì . Ëèñò
–
выпуклые
¹ äî êóì .
Ï î äï . Äàò à
множества. Их пересечение – область допустимых решений
ЗЛП, которая
Ðàçðàá.
является также выпуклым множеством.
Ï ðî â.
Ò.êî í ò ð.
Это множество называют также многоугольником решений. Он может
быть
Í .êî í ò ð.
ò â.
точкой, отрезком, лучом, ограниченным Óили
неограниченным
ÊÎÌÏÀÑ-3D LT V9 (íåêîììåð÷åñêàÿ âåðñèÿ)
многоугольником. (Случай вырождения, когда система ограничений (19) –
пустое множество и ЗЛП не имеет решения, исключается).
20
Ê
Ввиду неравенств x1  0 и x2  0 многоугольник решений всегда
находится в первом квадранте координатной плоскости Ox1 x2 .
Для нахождения экстремума целевой функции F воспользуемся
вектором набла  - градиентом F:
 F F 
  c1 , c2  .
  grad F  
,

x

x
 1
2 
Он показывает направление наискорейшего изменения целевой
функции F.
Прямая c1 x1  c2 x2   называется линией уровня функции F. Иными
словами на множестве всех точек
x1 , x2 
линии уровня функции F она
сохраняет постоянное значение  .
Алгоритм решения ЗЛП геометрическим методом.
1. Строится многоугольник решений.
2. Строится вектор набла, перпендикулярно ему проводятся линии
уровня и при этом учитывают, что оптимальное решение ЗЛП находится в
угловой точке многоугольника решений.
3. Первая точка встречи линии уровня с многоугольником решений
определяет минимум целевой функции.
4. Последняя точка встречи линии уровня с многоугольником решений
определяет максимум целевой функции.
5. Если линия уровня параллельна одной из сторон многоугольника
решений, то экстремум достигается во всех точках этой стороны A2 A3 . ЗЛП в
этом случае имеет бесконечное множество решений.
6. Для нахождения координаты точки экстремума решают систему из
двух уравнений прямых, дающих в пересечении эту точку.
21
Пример 1. Экономико-математическая модель задачи о планировании
производства.
Построим многоугольник решений. С этой целью запишем уравнения
x1
границ полуплоскостей из (17) в виде
 x1  x2  42

 x1  2 x2  48
 x1  4 x2  72
 x1 x2
 42  42  1
x
 1 x2
1
 
48
24

 x1  x2  1
 72 18
или
L1 
L2 
L3 
«Пробная» точка O0; 0  удовлетворяет всем неравенствам из (17) и
потому
многоугольник
решений
OA1 A2 A3 A4
расположен
в
нижних
полуплоскостях, порожденных прямыми L1 , L2 и L3 как показано на рис. 3
1
9 A2
координатами: x1  36 , x2  6 , являющимися решениями системы уравнений
 x1  x2  42 L1 
 x  2 x  48 L 
 1
2
2
L2
Подставив координаты точки A3 в целевую функцию, найдем
2 L1
Fmax  25  36  34  6  1104
1
0
x2
42
24
18 A1
L2





L1
A2
A3
A4
42 48
0
Рис. 3
22
L3
72
x1
L3
A3
3

Построим вектор набла   25, 34  . Последней точкой встречи линии
x2 A
уровня с многоугольником решений будет точка A3 (см. рис.3) с
Пример 2. Экономико-математическая модель задачи о диете.
Построим многоугольник решений. С этой целью запишем уравнения
границ полуплоскостей из (17) в виде
 x1 x2
 6  2  1 L1 
 x1  3x2  6
x
 1 x2

 1 L2 
3x1  x2  9 или  
3
9

 x1  8 x2  8
 x1  x2  1 L 
3
 8
1
«Пробная» точка O0; 0  удовлетворяет всем неравенствам из (17) и
потому многоугольник решений
A1 A2 A3 A4 A5 A6 расположен в верхних
полуплоскостях, порожденных прямыми L1 , L2 и L3 как показано на рис. 4
Построим вектор набла   8, 16  . Первой точкой встречи линии
уровня с многоугольником решений будет точка
A3 (см. рис. 4) с
координатами: x1  2,625 , x2  1,125 , являющимися решениями системы
уравнений:
L1 
L2 
 x1  3x2  6
3x  x  9
 1
2
Подставив координаты точки A3 в целевую функцию, найдем
f min  8  2,625  16  1,125  39
A2


9

A1


x2
L2
2
1
0
L1
L3
A3
A4
3
6
Рис. 4




23
A3
A4
L3
A5
8
A6
x1
Симплекс-метод для решения задач линейного программирования.
С увеличением числа неизвестных геометрический метод решения ЗЛП
становится затруднительным при трех переменных и невозможным при
большем числе переменных.
Поэтому был разработан универсальный метод решения ЗЛП –
симплекс-метод, позволяющий решать ЗЛП в канонической форме.
Изложим суть симплекс-метода на примере задач с 5 неизвестными.
Пусть ЗЛП приведена к виду
F  c0  c1 x1  c2 x2  max
(20)
при ограничениях:
 x3  p 0  p1 x1  p2 x2

 x4  q 0  q1 x1  q2 x2 ,

 x5  r0  r1 x1  r2 x2
(21)
где p 0  0, q 0  0, r0  0 ,
x1  0, x2  0, x3  0, x4  0, x5  0
(22)
Про систему ограничений (21) говорят, что она имеет допустимый вид,
если одни неизвестные ( x3 , x4 , x5 ) выражаются через остальные ( x1 , x2 ),
причем
свободные
члены
этих
выражений
неотрицательны
( p 0  0, q 0  0, r0  0 ).
Неизвестные x3 , x4 и x5 называются базисными, а неизвестные x1 , x2 –
свободными.
Возможны два принципиальных случая:
1 Все коэффициенты при свободных неизвестных в выражении для F
неположительны: c1  0 и c2  0 . Тогда для всякого неотрицательного
решения системы уравнений (21) имеем c1 x1  0 и c2 x2  0 , а потому
24
F  c0  c1 x1  c2 x2  c0 или max F  c0 .
Следовательно, базисное решение x1  0, x2  0, x3  p0 , x4  q0 , x5  r0
является оптимальными, т. е. задача решена.
2 Имеется свободное неизвестное, коэффициент при котором в
выражении для F положителен, а все коэффициенты при этом неизвестном в
уравнениях (21) – неотрицательны.
Для определенности положим c1  0, p1  0, q1  0, r1  0 . Исходя из
базисного решения, станем наращивать значение x1 , не меняя x2  0 . Тогда
значения базисных неизвестных будут оставаться неотрицательными:
x3  p 0  p1 x1  p0  0
x4  q 0  q1 x1  q0  0 ,
x5  r0  r1 x1  r0  0
а
значение
F  c0  c1 x1
будет
неограниченно
возрастать,
т.е.
max F   и задача решения не имеет.
Решения ЗЛП редуцируются к одному из случаев 1 или 2 путем
перехода к новому базису, в котором целевая функция не уменьшит своего
значения для базисного решения, а новая система ограничений должна иметь
допустимый вид. Преобразование базиса и перестройку целевой функции и
системы ограничений называют шагом в решении ЗЛП. Таким образом,
сделав нужное число шагов, решают ЗЛП (20) – (22).
Применим симплекс-метод к первой задаче.
I. Основная задача в примере 1 имеет вид
F  25 x1  34 x2  max
25
 x1  x2  42
 x  2 x  48
1
2
 x  4 x  72
2
 1
 x1  0, x2  0
Сначала приведем ее к каноническому виду, вводя балансовые
неизвестные x3  0 , x4  0 и x5  0 :
 x1  x2  x3  42

 x1  2 x2  x4  48
 x  4 x  x  72
2
5
 1
(23)
xi  0, i  1, 5
(24)
Теперь приведем (23) к допустимому виду – неизвестные x3 , x 4 и x5
выразим через x1 и x 2 , при этом свободные члены в правых частях
полученных уравнений неотрицательны:
 x3  42  x1  x2

 x4  48  x1  2 x2
 x5  72  x1  4 x2
(25)
Здесь x3 , x 4 и x5 – базисные неизвестные, а x1 и x 2 – свободные
неизвестные.
Шаг 1: положим в (25) x1  0 и x2  0 , тогда x3  42 , x4  48 , x5  72 .
Получим неотрицательное решение 0, 0, 42, 48, 72  системы уравнений (25).
Его называют базисным решением. Для него F  0 .
Шаг 2: положим в (25) x2  0 , а x1 начнем наращивать так, чтобы x3 ,
x 4 и x5 оставались неотрицательными, т. е.
x3  42  x1  0,
x4  48  x1  0,
x5  72  x1  0 .
Решая
неравенства,
найдем
эти
x1  min 42; 48; 72  42 . Тогда
x3  0 . Объявив
неизвестными, приведем (25) к допустимому виду:
26
наименьшее
x2 и
x3
значение
свободными
 x1  42  x2  x3

 x4  6  x2  x3
 x  30  3x  x
2
3
 5
(26)
Получим неотрицательное решение 42, 0, 0, 6, 30  системы уравнений
(26). Для него
F  25 x1  34 x2  25 42  x2  x3   34 x2  1050  9 x2  25 x3 (27)
примет значение F  1050 .
Сделаем выводы.
Во-первых, значение F по сравнению с 1-ым шагом увеличилось.
Во-вторых, в (27) коэффициент при
x3
отрицательный и для
дальнейшего увеличения значения F надо положить x3  0 и наращивать x 2 .
Шаг 3: положим в (26) x3  0 , а x 2 начнем наращивать так, чтобы x1 ,
x 4 и x5 оставались неотрицательными, т. е.
x1  42  x2  0,
x4  6  x2  0,
x5  30  3x2  0 .
30 

Откуда находим наименьшее значение x2  min 42; 6;   6 . Тогда
3

x4  0 . Объявив x3 и x 4 свободными неизвестными, приведем (27) к
допустимому виду:
 x1  36  2 x3  x4

 x2  6  x3  x4
 x5  12  2 x3  3x4
(28)
Получили неотрицательное решение 36, 6, 0, 0, 12  системы уравнений
(28). Для него
F  1050  9 6  x3  x4   25 x3  1104  16 x3  9 x4
примет значение F  1104 .
Сделаем выводы.
27
(29)
Во-первых, значение F по сравнению со 2-ым шагом увеличилось.
Во-вторых, в (29) оба коэффициента при свободных неизвестных
отрицательны и дальнейшее увеличение значения F невозможно:
Fmax  1104
при x3  x4  0 . Задача решена. Учитывая экономический смысл
неизвестных, приходим к выводу: предприятие получит наибольшую
прибыль 1104 единиц при изготовлении 36 единиц товара T1 и 6 единиц
товара T2 , при этом остатки ресурсов S1 и S 2 равны нулю ( x3  x4  0 ), а
остаток ресурса S 3 равен 12 единицам.
Если решается ЗЛП, в которой требуется найти минимум целевой
функции, то задачу либо сводят к рассмотренной выше задаче с целевой
функцией f   F , либо с помощью шагов приводят к одному из двух
принципиальных случаев:
1 Все коэффициенты при свободных неизвестных в выражении для F
неотрицательны:
c1  0
и
c2  0 .
Тогда
базисное
решение
x1  0, x2  0, x3  p0 , x4  q0 , x5  r0 является решением задачи.
2 Имеется свободное неизвестное, коэффициент при котором в
выражении для F (20) отрицателен, а все коэффициенты при этом
неизвестном в уравнениях (21) – неотрицательны. Тогда задача решения не
имеет.
Применим симплекс-метод ко второй задаче, Основная задача в
примере 2 имеет вид
f  8 x1  16 x2  min
 x1  3 x2
3 x  x
 1
2

 x1  8 x2
 x1  0,
28
6
9
8
x2  0
Сначала приведем ее к каноническому виду, вводя балансовые
неизвестные x3  0 , x4  0 и x5  0 :
 x1  3x2  x3  6

3x1  x2  x4  9
x  8x  x  8
2
5
 1
xi  0, i  1, 5
(30)
(31)
Приведем ограничения (30) к допустимому виду. Как показано выше, в
качестве базисных неизвестных следует выбирать такие неизвестные, каждая
из которых входит только в одно из уравнений системы ограничений (31),
при этом нет таких уравнений системы, в которые не входит ни одна из этих
неизвестных, и каждая базисная неизвестная имеет тот же знак, что и
свободный член.
Нетрудно видеть, что x3 , x 4 и x5 не могут быть базисными
неизвестными. Действительно,
 x3  6  x1  3x2

 x4  9  3x1  x2
 x  8  x  8 x
1
2
 5
(32)
и знаки x3 , x 4 и x5 противоположны знакам свободных членов.
Для выделения базисных неизвестных из системы ограничений (30)
необходима ее перестройка.
Полагая
в
(32)
x1  0
(или
x2  0 )
найдем
из
условий
неотрицательности x3 , x 4 и x5 :
x3  6  3x2  0,
x4  9  x2  0,
x5  8  8 x2  0 .
наибольшее значение x2  max 2; 9; 1  9 . Тогда x4  0 и систему (32)
запишем в виде
29
 x2  9  3x1  x4

 x3  21  8 x1  3x4
 x  64  23 x  8 x
1
4
 5
(33)
Получили систему ограничений, имеющую допустимый вид: x 2 , x3 и
x5 – базисные неизвестные, x1 и x 4 – свободные неизвестные. Перейдем к
процедуре шагов.
Шаг 1: положим в (33) x1  0 и x4  0 , тогда получим базисное
решение 0, 9, 21, 0, 64 , для которого целевая функция
f  8 x1  16 x2  8 x1  16 9  3x1  x4   144  40 x1  16 x4
(34)
примет значение f  144 .
В (5.15) коэффициент при x 4 положительный и для дальнейшего
уменьшения значения f надо положить x4  0 и наращивать x1 .
Шаг 2: положим в (33) x4  0 , а x1 начнем наращивать так, чтобы x 2 ,
x3 и x5 оставались неотрицательными, т. е.
x2  9  3x1  0,
x3  21  8 x1  0,
x5  64  23 x1  0 .
 9 21 64  21
Откуда находим x1  min  ; ;   . Тогда x3  0 . Объявив x3 и
 3 8 23  8
x 4 свободными неизвестными, приведем (33) к допустимому виду:
21 1
3

x


x

x4
1
3

8 8
8

9 3
1

 x 2   x3  x 4
8 8
8

29 23
5

 x5  8  8 x 3  8 x 4

30
(35)
29 
 21 9
Из (35) получим базисное решение  ; ; 0; 0;  . Для него
8 
8 8
3 
 21 1
f  144  40   x3  x4   16 x4  39  5 x3  x4 (36)
8 
8 8
примет значение f  39 .
В (36) коэффициенты при свободных неизвестных положительны и
дальнейшее уменьшение значения f невозможно: f min  39 при x3  x4  0 .
Задача решена.
Учитывая экономический смысл неизвестных, приходим к выводу.
Ежесуточная
диета,
обеспечивающая
необходимое
количество
питательных веществ, состоит из x1  2,625 единиц продукта P1 , x2  1,125
единиц продукта P2 и ее минимальная стоимость F  39 единиц. При этом
потребности организма в питательных веществах A и B отвечают требуемым
минимальным объемам V  6 единиц и V  9 единиц соответственно (т.к.
x3  0 и x4  0 ), а потребности в питательном веществе С больше требуемого
минимального объема V  8 единиц на x5  3,625 единиц.
В заключение рассмотрим вопрос: всегда ли после конечного числа
шагов
симплекс-метод
закончится
либо
нахождением
оптимального
решения, либо установлением того факта, что задача не имеет решения.
Ответ утвердительный и содержится в следующей теореме.
Теорема. Если существует оптимальное решение ЗЛП, то существует и
базисное оптимальное решение. Последнее всегда может быть получено с
помощью симплекс-метода.
Симплекс-таблицы для решения ЗЛП.
Метод искусственного базиса (М-метод).
Описанный процесс решения ЗЛП симплекс-методом довольно
трудоемкий и требует выполнения однообразных преобразований. Причем с
возрастанием числа неизвестных растет и число шагов.
31
Оказывается,
эти
преобразования
можно
записать
в
виде
последовательности однотипно заполненных таблиц, называемых симплекстаблицами.
Изложим способ составления и преобразования таких таблиц на
примерах первой и второй основных задач .
I. Первая основная задача.
Для заполнения первой симплекс-таблицы необходимо переписать
целевую функцию F и систему ограничений в виде:
F  25 x1  34 x2  0
 x1  x2  x3  42

 x1  2 x2  x4  48
 x1  4 x2  x5  72
Заполним таблицу
Базисные Свободные
неизвестные
члены
42
x3
48
x4
72
x5
F
0
x1
x2
x3
x4
x5
1
1
1
–25
1
2
4
–34
1
0
0
0
0
1
0
0
0
0
1
0
В выражении для F выясняем, имеются ли в последней строке таблицы,
кроме столбца «свободные члены», отрицательные числа. Если таковых нет,
то задача решена. Если же есть, то выполняем преобразование: в столбце x1
имеем  25  0 (из двух отрицательных чисел –25 и –34 выбирают меньшее
по модулю), над этим элементом ищем положительные числа. Если таковых
нет, то задача не имеет решения. В нашем случае над –25 есть три
положительных числа: 1; 1 и 1.
Найдем
 42 48 72  42
min  , ,  
 42
1 1 1 1
32
Элемент, стоящий на пересечении строки ( x3 ) и столбца ( x1 ), называем
разрешающим. В нашем случае он равен 1. (Если разрешающий элемент
равен числу m  1, то всю строку делят на разрешающий элемент m, чтобы
получить 1). Неизвестная x1 вводится в базис, а неизвестная x3 выводится из
него.
Заполняем вторую симплекс-таблицу. Строка ( x3 ) из первой таблицы
становится в ней строкой ( x1 ). Далее преобразуем строки ( x 4 ), ( x5 ) и (F)
первой таблицы так, чтобы их элементы, стоящие в столбце ( x1 ), обратились
в 0. С этой целью
1)
вычтем элементы строки ( x1 ) из соответствующих элементов
строки ( x 4 ), и запишем полученные результаты в строку ( x 4 ) второй
таблицы;
2)
вычтем элементы строки ( x1 ) из соответствующих элементов
строки ( x5 ), и запишем полученные результаты в строку ( x5 ) второй
таблицы;
3)
умножим элементы строки ( x1 ) на 25, сложим с соответствующими
элементами строки (F), и запишем полученные результаты в строку (F)
второй таблицы.
В результате получим следующую симплекс-таблицу
Базисные Свободные
неизвестные
члены
42
x1
6
x4
30
x5
F
1050
x1
x2
x3
x4
x5
1
0
0
0
1
1
–1
–1
25
0
1
0
0
0
0
1
0
1
3
–9
В строке (F) есть отрицательное число –9. Поэтому продолжим поиск
оптимального решения. Над –9 есть три положительных числа: 1; 1 и 3.
Найдем
33
 42 6 30  6
min  , ,    6
1 1 3 1
Элемент, стоящий на пересечении строки ( x 4 ) и столбца ( x 2 )
разрешающий и равен 1. Неизвестная x 2 вводится в базис, а неизвестная x 4
выводится из него.
Заполняем третью симплекс-таблицу. Строка ( x 4 ) из второй таблицы
становится в ней строкой ( x 2 ). Далее преобразуем строки ( x1 ), ( x5 ) и (F)
второй таблицы так, чтобы их элементы, стоящие в столбце ( x 2 ), обратились
в 0. С этой целью
1)
вычтем элементы строки ( x 2 ) из соответствующих элементов
строки ( x1 ), и запишем полученные результаты в строку ( x1 ) третьей
таблицы;
2)
умножим элементы строки ( x 2 ) на 3, вычтем из соответствующих
элементов строки ( x5 ), и запишем полученные результаты в строку ( x5 )
третьей таблицы;
3)
умножим элементы строки ( x 2 ) на 9, сложим с соответствующими
элементами строки (F), и запишем полученные результаты в строку (F)
третьей таблицы.
В результате получим следующую симплекс-таблицу
Базисные Свободные
неизвестные
члены
36
x1
6
x2
12
x5
F
1104
x1
x2
x3
x4
x5
1
0
0
0
0
1
0
0
2
–1
2
16
–1
1
–3
9
0
0
1
0
В строке (F) нет отрицательных чисел. Получили оптимальное
решение:
34
Fmax  1104
при x1  36 , x2  6 , x3  x4  0 , x5  12 .
Замечание. Симплекс-таблицы удобнее «пристыковывать» друг к другу
по вертикали, что позволяет не писать многократно заглавную строку
II. Вторая основная задача.
Для заполнения первой симплекс-таблицы перепишем целевую
функцию F и систему ограничений (6.14), имеющую допустимый вид,
следующим образом:
F  40 x1  16 x4  144
3x1  x2  x4  9

8 x1  x3  3x4  21
23 x  8 x  x  64
4
5
 1
Заполним таблицу
Базисные Свободные
неизвестные
члены
9
x2
21
x3
64
x5
F
144
1,125
x2
2,625
x1
3,625
x5
F
39
x1
x2
x3
x4
x5
3
1
0
0
0
1
0
0
0
0
1
0
0
–0,375
0,125
–2,875
–5
–1
–3
–8
–16
0,125
–0,375
0,625
–1
0
0
1
0
0
0
0
0
8
23
40
0
1
0
0
В выражении для F выясняем, имеются ли в последней строке таблицы,
кроме столбца «свободные члены», положительные числа. Если таковых нет,
то задача решена. Если же есть, то выполняем преобразование: в столбце x1
имеем 40  0 . Над этим элементом ищем положительные числа. Если
таковых нет, то задача не имеет решения. В нашем случае над 40 есть три
положительных числа: 3; 8 и 23.
35
Найдем
 9 21 64  21
min  , ,    2,625
 3 8 23  8
Элемент, стоящий на пересечении строки ( x3 ) и столбца ( x1 )
разрешающий и равен 8. Неизвестная x1 вводится в базис, а неизвестная x3
выводится из него. Все элементы строки ( x3 ) разделим на разрешающий
элемент. Полученные результаты запишем в новую симплекс-таблицу в
строке ( x1 ).
Преобразуем строки ( x 2 ), ( x5 ) и (F) первой таблицы так, чтобы их
элементы, стоящие в столбце ( x1 ), обратились в 0. С этой целью
1) умножим элементы строки ( x1 ) на 3, вычтем из соответствующих
элементов строки ( x 2 ), и запишем полученные результаты в строку ( x1 )
второй таблицы;
2) умножим элементы строки ( x1 ) на 23, вычтем из соответствующих
элементов строки ( x5 ), и запишем полученные результаты в строку ( x5 )
второй таблицы;
3) умножим элементы строки ( x1 ) на 40, вычтем из соответствующих
элементов строки (F), и запишем полученные результаты в строку (F) второй
таблицы.
В строке (F) нет положительных чисел. Получили оптимальное
решение: Fmin  39
при x1  2,625 , x2  1,125 , x3  x4  0 , x5  3,625 .
Замечание. Первая симплекс-таблица второй основной задачи была
заполнена
с
учетом
того,
что
система
ограничений
(6.11)
была
предварительно сведена к допустимому виду (6.14), т.е. был найден
допустимый базис. Зачастую поиск такого базиса довольно затруднителен.
36
Рассмотрим следующий метод нахождения допустимого базиса, который
называют методом искусственного базиса или М-методом.
Метод искусственного базиса (М-метод).
Применительно к рассматриваемой задаче М-метод заключается в
следующем. В каждое уравнение системы ограничений (6.11), введем свою
новую искусственную неизвестную: y1  0 , y 2  0 и y3  0 . Включим их в
число базисных неизвестных и составим новую функцию цели
G  F  M  y1  y 2  y3  ,
где М – произвольно большое положительное число.
В результате получили следующую ЗЛП, приведенную к допустимому
виду
G  8 x1  16 x2  M  y1  y 2  y3   min
 y1  6  x1  3x2  x3

 y 2  9  3x1  x2  x4
 y  8  x  8x  x
1
2
5
 3
xi  0, i  1, 5,
y j  0,
y  1, 3 .
Эту задачу называют М-задачей.
Сформулируем
утверждения,
устанавливающие
связь
между
решениями исходной задачи и М-задачи.
1.
Если в оптимальном решении М-задачи все искусственные
переменные равны 0, то соответствующие значения остальных переменных
дают оптимальное решение исходной задачи (т.е.
Gmin  Fmin , если
y1  y 2  y3  0 ).
2.
Если имеется оптимальное решение М-задачи, в котором хотя бы
одна из искусственных переменных отлична от 0, то исходная задача не
имеет допустимого решения.
37
3.
Если М-задача не имеет оптимального решения, то исходная
задача неразрешима (т.е. если Gmin   , то либо Fmin   , либо нет ни
одного допустимого решения).
Из этих утверждений следует следующее правило решения M-задачи
симплекс-методом:
а) Необходимо выбирать последовательность шагов таким образом,
чтобы все искусственные неизвестные y1 , y 2 , y3 вышли из базиса, т.е. стали
свободными.
б) В симплекс-таблице отбросив столбцы для этих неизвестных,
получим симплекс-таблицу, дающую оптимальное решение исходной задачи.
в) Если при решении М-задачи получена симплекс-таблица, дающее
оптимальное решение, и в этой таблице хотя бы одна искусственная
переменная y i входит в базис, причем в строке для y i свободный член
положителен, то исходная задача не имеет ни одного допустимого решения.
Составим симплекс-таблицы решаемой задачи.
Базис Свобод
ные
ные
x1
x2
x3
неизв члены
ест
ные
3
–1
y1
6
1
9
3
1
0
y2
8
1
0
y3
8
5M  8 12 M  16  M
G
23M
58
y1
y2
3
8
23 8
0
0
x2
1
18
1
G
y1
x1
x4
x5
y1
y2
y3
0
–1
0
0
0
–1
M
M
1
0
0
0
0
1
0
0
0
0
1
0
–1
0
0
–1
38
0
1
3 8
18
1
0
0
0
1 8
0
0
18
11M  16
7M
6
2
0
M
M
M
2
2
29 23
0
1
0
0
–1
0
5 23
8 23
 8 23
1 23
64 23
38
1 8

3M
2
2
0
0
1
0
 5 23
 8 23
8 23
 1 23
x2
G
15 23
29 M  752
23
0
1
0
0
0
1 23
 3 23
M
5M  48
23
8M  40
23
0
58
1
23 8
5 8
–1
1 8
38
38
1 8
0
0
 M 1
M
 23 8
x5
29 8
0
0
x1
x2
21 8
0
1
18
3 8
98
1
0
3 8
18
0
0
G
39
0
0
–5
–1
0
39
0
M 5
 1 23

47 M  12 
23
3 23
 31M  40
23
ЛЕКЦИЯ 6
Динамическое программирование. Принцип оптимальности и
функциональности. Функциональное уравнение Беллмана
Теории управления – развивающаяся область современной математики.
Ей посвящена обширная литература , в которой исследуются различные типы
управленческих систем. Рассмотрим классический метод оптимизации
процесса управления, разработанный Р. Беллманом.
Пусть экономический процесс управляемый, т. е. возможно влияние на
ход его развития.
Под управлением понимается совокупность решений, принимаемых на
каждом этапе развития экономического процесса и направленных на его
оптимизацию.
Примерами управляемых процессов являются распределение средств
между предприятиями, использование ресурсов в течение ряда лет, замена
оборудования, пополнение запасов и др.
Динамическое программирование (ДП) – раздел математического
программирования, в котором процесс принятия решений и управления
является многошаговым.
Схема процесса принятия решений методом ДП представлена на рис. 5
0
1
2


S2



Xk
k


Sk



4
Номер шага
n
(время)
S0
S1
X1
X2
Sn=S
*
Состояния
Управления
Рис. 5
В результате управления экономическая система S переводится из
начального состояния S 0 в конечное состояние S  . Процесс разбит на n
шагов, на каждом из которых принимается решение (управление) X k ,
k  1, n .
40
Состояние S k
системы S в конце k-го шага зависит лишь от
предшествующего состояния S k 1 и управления X k и не зависит от
остальных предшествующих состояний и управлений. Такое требование
называется
в
теории
управления
Беллмана
условием
отсутствия
последействия, согласно которому уравнения состояний S k имеют вид:
S k   k S k 1 , X k  , k  1, 2, , n . (37)
Обозначим показатель эффективности (оптимальности) k-го шага через
f k S k 1 , X k , k  1, 2, , n .
Тогда согласно еще одному требованию в теории управления
Беллмана, называемому условием аддитивности, целевая функция имеет вид
n
F   f k S k 1 , X k 
(38)
k 1
Таким образом, задача ДП (ЗДП) формулируется так: найти такое
управление X   X 1 , X 2 , , X n  , переводящее систему S из состояния S 0 в
состояние S  , при котором целевая функция (38) принимает экстремальное
значение.
Сформулируем принцип оптимальности Беллмана:
Каково бы ни было состояние системы перед очередным шагом, надо
выбрать управление на этом шаге так, чтобы выигрыш на данном шаге и
оптимальный выигрыш на всех последующих шагах был максимальным.
Рассмотрим n-ый шаг. По принципу оптимальности X n нужно выбрать
так,
чтобы
для
любых
состояний
S n1
получить
экстремум
(для
определенности возьмем максимум) целевой функции на этом шаге.
Обозначим
Fn S n1   max f n S n1 , X n 
Xn
41
(39)
Решение X n , при котором достигается Fn S n1  , также зависит от S n1
и называется условно-оптимальным управлением на n-ом шаге. Обозначим
его через X n S n1  .
Для остальных шагов по принципу оптимальности


Fk S k 1   max f k S k 1 , X k   Fk1 S k  , k  n  1, n  2, , 1 (40)
Xk
Уравнения (39) и (40) называют функциональными уравнениями
Беллмана. Они по сути рекуррентные соотношения, позволяющие найти
предыдущее значение функции, зная последующие.
Рассмотрим решение конкретных ЗДП.
Пример 1. Задача оптимального распределения оборудования.
Производственное объединение распределяет средства в четыре
дочерние фирмы на покупку пяти производственных линий. Эксплуатация
производственной линии в дочерней фирме под номером k k  1, 2, 3, 4  в
зависимости от количества выделенных этой дочерней фирме линий xk
приносят прибыль f k  xk  . Функции f k  xk  заданы таблицей 3.
xk
1
2
3
4
5
f1  x k 
12
17
20
22
26
f 2  xk 
14
16
18
20
24
f 3  xk 
16
18
21
24
26
Таблица 3
f 4  xk 
14
15
18
20
24
Найти, какое количество производственных линий нужно выделить
каждой дочерней фирме, чтобы суммарная прибыль была максимальной.
Решение. Примем следующие обозначения:
42
X k  xk – количество производственных линий, выделяемых дочерней
фирме под номером k , k  1, 2, 3, 4 ;
4
F   f k  xk  – суммарная прибыль, получаемая от эксплуатации
k 1
производственных линий в четырех дочерних фирмах;
S 0  5 – начальное состояние системы, т. е. наличие производственных
линий до начала их распределения по фирмам;
S1  5  x1 – состояние системы после первого шага, когда первой
фирме выделили x1 производственных линий;
S 2  S1  x2 – состояние системы после второго шага, когда второй
фирме выделили x 2 производственных линий;
S 3  S 2  x3 – состояние системы после третьего шага, когда третьей
фирме выделили x3 производственных линий;
S 4  S 3  x4  0 – состояние системы после четвертого шага, когда
четвертой фирме выделили x 4 производственных линий.
ЭММ задачи примет вид
4
F   f k  xk   max
k 1
при условиях
4
 x k  5
k 1
 xk  0, k  1, 4.
Отметим, что заданные функции f k x , k  1, 4 , заменяют показатели
эффективности k-го шага f k S k 1 , X k  , содержащиеся в функциональных
уравнениях Беллмана (39) и (40), т. е.
f k S k 1 , X k   f k xk , k  1, 4 .
43
Результаты анализа возможных размещений производственных линий
сведены в таблицу 4.
Первая строка нулевая (нет производственных линий, следовательно,
нет прибыли).
В столбец 1 внесены возможные распределения линий S k 1 в конце
k  1 -го шага, изменяющиеся от 0 до 5.
В столбец 2 внесены возможные управления xk на k-ом шаге для
заданного количества производственных линий S k 1 0  xk  S k 1  .
В столбец 3 внесены данные о возможных оставшихся после k-го шага
количествах линий S k , найденные из уравнения состояния S k  S k 1  xk .
Анализ состояния системы начнем с последнего (четвертого) шага.
Запишем функциональное уравнение Беллмана (39):
F4 S3   max f 4  x4  .
0  x4  S3
Из уравнения состояния S 4  S 3  x4  0 (все производственные линии
распределены) находим x4  S 3 и потому
F4 S 3   f 4 S 3 , S 3  0, 5 .
Переходим к третьему шагу. Запишем функциональное уравнение
Беллмана (40):


F3 S 2   max f 3 x3   F4 S3  .
0  x3  S2
Пусть S k 1  S 2  1 , тогда возможны два варианта:
1)
x3  0 , S 3  1
f 3  x3   F4 S 3   f 3 0  f 4 1  0  14  14 ,
2)
x3  1 , S 3  0
f 3  x3   F4 S 3   f 3 1  f 4 0  16  0  16 .
44
Наибольшее значение из двух полученных (14 и 16) равно 16.
Следовательно, условный максимум целевой функции – F3 S 2   16 (строка 2
столбца 5), который достигается при условно оптимальном количестве
производственных линий, вложенных в третью фирму, равном 1, т. е.
x3 S 2   1 (строка 2 столбца 6).
Аналогично проводятся расчеты для случаев S k 1  S 2  2 , S k 1  S 2  3 ,
S k 1  S 2  4 и S k 1  S 2  5 (строки 3, 4, 5 и 6 столбцов 4, 5 и 6).
Второй шаг. Запишем функциональное уравнение Беллмана (14.4):


F2 S1   max f 2 x2   F3 S 2  .
0  x2  S1
Пусть S k 1  S1  1 , тогда возможны два варианта:
1)
x2  0 , S 2  1
f 2  x2   F3 S 2   f 2 0  F3 1  0  16  16 ,
2)
x2  1 , S 2  0
f 2  x2   F3 S 2   f 2 1  F3 0  14  0  14 .
Условный максимум целевой функции – F2 S1   16 при x2 S1   0 .
Пусть S k 1  S1  2 , тогда возможны три варианта:
1)
x2  0 , S 2  2
f 2  x2   F3 S 2   f 2 0  F3 2  0  30  30 ,
2)
x2  1 , S 2  1
f 2  x2   F3 S 2   f 2 1  F3 1  14  16  30 ,
3)
x2  2 , S 2  0
f 2  x2   F3 S 2   f 2 2  F3 0  16  0  16 .
Условный максимум целевой функции – F2 S1   30 при x2 S1   1.
45
Аналогично проводятся расчеты для случаев S k 1  S1  3 , S k 1  S1  4
и S k 1  S1  5 .
Первый шаг. Запишем функциональное уравнение Беллмана (14.4):


F1 5  max f1 x1   F2 S1  .
0  x1 5
Приведем расчеты аналогично предыдущему и заполним таблицу 14.2.
В результате получим следующие выводы:
а) Максимальная прибыль от внедрения производственных линий в
первую дочернюю фирму составит
Fmax  F1 S 0  5  61 ден. ед.
x1
при оптимальном внедрении двух производственных линий
S 0  5   2 .
б) Оптимальное количество линий, оставшихся в конце первого шага,
S1  S 0  x1 S 0   5  2  3
В столбце 9 таблицы 14.2 находим x2 3  1 (строка 4). Оставшиеся три
дочерние фирмы принесут прибыль 44 ден. ед. при вложении во вторую
фирму одной линии x2 3  1 .
в) Оптимальное количество линий, оставшихся в конце второго шага,
S 2  S1  x2 3  3  1  2
В столбце 6 таблицы 14.2 находим x3 2   1 (строка 3). Оставшиеся две
дочерние фирмы принесут прибыль 32 ден. ед. при вложении в третью фирму
одной линии x3 1  1 . Оставшаяся одна линия вкладывается в четвертую
фирму, которая принесет прибыль 14 ден. ед.
Ответ: оптимальное решение задачи X  2, 1, 1, 1 при F   61 ден. ед.
46
Таблица 4
k 3
f 2 x2  
 F3 S 2 
Номер
строки
f 3 x3  
 F S3 

4
1
1
2
0
1
2
2
3
3
4
4
5
3
4
k 1
k 2
f1 x1  
 F2 S1 
5
6
7
8
0 0 0
0 1 0+
1 14=14
0
6
16
+0=16
0
1
0
1
0 2 0+
1 15=15
1
0
2 0 16
+14=30
18
+0=18
3
0 3 0+
1 18=18
2
2
2 1 16
3 +15=31
0
18
+14=32
21
+0=21
3
0 4 0+
1 20=20
3
5
2 2 16
3 +18=34
1
4 0 18
+15=33
21
+14=35
24
+0=24
3
0
0
1
0
+16=1
6
1
4+0=1
4
1
0
+30=3
0
1
4+16=
30
1
6+0=1
6
2
0
+32=3
2
1
4+30=
44
1
6+16=
32
1
8+0=1
8
3
0
+35=3
5
1
4+32=
46
1
6+30=
46
1
47
6
3
0
4
4
4
6
1
9
0
0
0
0
0
+16=1
6
1
2+0=1
2
1
0
+30=3
0
1
2+16=
28
1
7+0=1
7
1
0
+44=4
4
1
2+30=
42
1
7+16=
33
2
0+0=2
0
1
0
+46=4
6
1
2+44=
58
1
7+30=
47
2
1
1
2
0
1
1
3
0
4
0
5
1
0
0
6
0
4
8
5
6
0 5 0+
1 24=24
4
8
2 3 16
3 +20=36
2
4 1 18
5 +18=36
0
21
+15=36
24
+14=38
26
+0=26
3
8+16=
34
2
0+0=2
0
4
0
+38=3 9
8
1
4+35=
49
1
6+32=
48
1
8+30=
48
2
0+16=
36
2
4+0=2
4
48
4
0+16=
36
2
2+0=2
2
1
0
+49=4 1
9
1
2+46=
58
1
7+44=
61
2
0+30=
50
2
2+16=
38
2
6+0=2
6
6
2
ЛЕКЦИЯ 7
Модели потребительского выбора. Функция полезности. Линии
безразличия. Оптимизация функции полезности. Функции спроса и
предложения.
Пусть потребитель, располагая некоторой суммой средств, полностью
тратит ее на приобретение товаров. Набор товаров покупает исходя из
имеющейся суммы средств и собственных предпочтений. Математическая
модель поведения такого потребителя называется моделью потребительского
выбора.
Функция полезности
Рассмотрим потребительский набор из двух товаров ( x, y ), где x и y –
количество единиц первого и второго товаров соответственно. Потребительский
набор – это точка в прямоугольной системе координат xOy с координатами
( x, y ).
Отношение потребителя к различным наборам товаров называют выбором
потребителя.
Если каждому набору ( x, y ) поставить в соответствие потребительскую
оценку этого набора в виде некоторого числа u, то получим функцию
полезности потребителя u( x, y ).
Пусть набор A  ( x1 , y1 ) предпочтительнее набора B  ( x2 , y 2 ) . Тогда
оценка потребителем набора
A  ( x1 , y1 )
превосходит оценку набора
B  ( x2 , y 2 ) , т.е. u  A  u B  . Каждый потребитель имеет свою функцию
полезности.
Свойства функции полезности
1. Возрастание
потребления
одного
продукта
потреблении другого приводит к росту функции полезности:
при x1  x имеем u  x1 , y   u  x, y  ;
49
при
постоянном
при y1  y имеем u  x, y1   u  x, y  .
Отсюда следует
ux, y 
 0.
y
u x, y 
 0,
x
Первые частные производные от функции полезности потребителя
называются предельными полезностями соответствующих продуктов:
u  x, y 
– предельная полезность первого продукта;
x
u  x, y 
– предельная полезность второго продукта.
y
2. Функция полезности должна быть, по крайней мере, дважды
дифференцируемой.
Частная
производная
от
предельной
полезности
продукта по той же переменной должна быть отрицательной, т.е. предельная
полезность уменьшается с ростом этой переменной (этого продукта). Отсюда
следует, что вторые частные производные по тому же аргументу должны быть
отрицательны, т.е.
 2u
 0.
y 2
 2u
 0,
x 2
Это свойство называется законом убывания предельной полезности.
3. Вторая частная производная от предельной полезности продукта по
другой переменной должна быть положительной, т.е. предельная полезность
увеличивается с ростом другой переменной (другого продукта). Таким
образом,
 2u
 2u

 0.
xy yx
50
Если функция полезности в задаче потребительского выбора не обладает
свойствами 2 и 3, она тем не менее может описывать реальное поведение
потребителя.
Линии безразличия
Линии уровня функции полезности потребителя называются линиями
безразличия.
Линии безразличия являются функциями одной переменной. Данная
функция имеет вид:
u  x, y    ,
где   const .
Множество линий безразличия называется картой линий безразличия
(рис. 5).
На рис. 5 изображены линии безразличия, имеющие уровни
полезности потребителя 1 ,  2 и  3 . Линии безразличия не касаются и не
пересекаются. При увеличении уровня функции полезности  линии
безразличия смещаются вправо вверх. Для примера рис. 11.1 справедливо
неравенство 1   2   3 .
y

3

2

1
0
x
Рис. 5 Линии безразличия
51
y
Из приведенных выше свойств функции полезности следует, линия
безразличия в системе координат хОу является убывающей и выпуклой вниз
(вогнутой) функцией.
Если рассматривать дифференциал функции полезности u  x, y  при
движении вдоль линии уровня, то видно, что он равен нулю. Это связано с
тем, что значение функции при этом не изменяется. Таким образом,
dux, y  
ux, y 
ux, y 
dx 
dy  0 .
x
y
Отсюда следует, что
dy
ux, y  ux, y 
.

dx
x
y
(41)
 dy 
Производная    называется предельной нормой замены первого
 dx 
продукта вторым.
Так как числитель и знаменатель дроби – величины положительные
(свойство 1), то производная функции безразличия
y  yx 
является
отрицательной, т.е. данная функция является убывающей.
Вторая
производная
y  yx 
функции
находится
дифференцирования (41):

 u  x, y  u  x, y  
 dy 

d    

x

y
dx
  

dx
x
 2 u  x, y  u  x, y  u  x, y   2u  x, y  .




y
x
yx
x 2
 u  x, y  



y


52
2
путем
Так как первое слагаемое числителя положительно в силу свойств 1 и 2
функции полезности, второе слагаемое числителя также положительно в силу
свойств 1 и 3 функции полезности, то вторая производная функции
безразличия y  y  x  является величиной положительной. Отсюда следует,
что линии безразличия выпуклы к низу.
Если перейти от бесконечно малых приращений dx и dy к конечным
приращениям x и y , то можно записать следующее приближенное
равенство:
dy y
.

dx x
Сопоставив данное выражение с (41), найдем

y ux, y  ux, y 
.

x
x
y
(42)
 y 
Дробь  
 называется нормой замены первого продукта вторым.
 x 
Норма замены показывает, насколько изменится потребление второго продукта
при изменении потребления первого продукта на единицу. Если известна
функция полезности u ( x, y) то норма замены рассчитывается по формуле
(42).
Пример. Пусть в течение месяца потребляется 45 единиц продукта х и 36
единиц продукта у. Функция полезности потребителя задана соотношением
u  xy .
Определить величину, на которую потребитель должен увеличить
потребление второго продукта при уменьшении потребления первого на десять
единиц.
Решение. Норму замены первого продукта вторым находят из
соотношения (42):
53

y y 45
 
 1,25
x x 36
При уменьшении потребления продукта х на 10 единиц потребление
продукта у возрастет на 12,5 единиц. Действительно,
y  1,25   10   12,5
Таким образом, норма замены показывает, на сколько должен
потребитель увеличить (уменьшить) потребление второго продукта, если он
уменьшил (увеличил) потребление первого продукта на заданную величину.
Оптимизация функции полезности
Естественно, что потребитель желает так использовать имеющиеся у
него средства, чтобы получить максимальную пользу при затрате некоторого
заданного их количества.
Задачей потребительского выбора называется определение такого
потребительского набора, который максимизирует функцию полезности
потребителя при заданном бюджетном ограничении. Этот набор называют
оптимальным для потребителя, или локальным рыночным равновесием
потребителя.
Бюджетным ограничением
называется
денежная
сумма
(доход),
предназначенная на покупку данного набора товаров.
Если товаров два, то бюджетное ограничение I и цены на первый p1 и
второй p 2 товары связаны соотношением
p1 x  p2 y  I .
(43)
Задачу математического выбора можно записать в виде ЗМП:
u  x, y   max
при условиях
54
p1 x  p2 y  I ,
x  0,
y  0,
(44)
При решении задачи математического выбора (44) обычно бюджетное
ограничение p1 x  p2 y  I заменяют на равенство p1 x  p2 y  I . Это связано с
тем, что значение функции полезности увеличивается при увеличении x и y.
Максимум лежит на крайних правых и нижних точках. Следовательно, задачу
математического программирования можно заменить задачей на условный
экстремум: u  x, y   max при условиях
p1 x  p2 y  I  0,
x  0,
y  0,
(45)
где u  x, y  - целевая функция; p1 x  p2 y  I  g  x, y  – функция связи.
Функция Лагранжа для этой задачи имеет вид:
L x, y,    u  x, y     p1 x  p2 y  I  .
Составляем систему линейных уравнений, для чего приравниваем к нулю
первые частные производные функции Лагранжа:
Lx, y,   u x, y 

 p1  0 ;
x
x
Lx, y,   ux, y 

 p2  0 ;
y
y
L x, y,  
 p1 x  p2 y  I  0 .

Умножим первое уравнение на p 2 , а второе – на p1 и вычтем второе
уравнение из первого:
ux, y 
ux, y 
p2 
p1  0 .
x
y
55
Таким образом, систему уравнений для укороченной подозрительной точки
функции Лагранжа можно переписать в виде:
u x, y  u x, y  p1
;

x
y
p2
p1 x  p2 y  I .
Сопоставив (46) с (42), получим 
(46)
(47)
y p1
,

x p2
т.е. норма замены первого продукта вторым равна отношению цены первого
продукта к цене второго.
Геометрический смысл условного экстремума функции F  f  x, y  в точке
x
0



, y 0 состоит в том, что градиенты целевой функции grad f x 0 , y 0 и функции




связи grad g x 0 , y 0 , выходящий из точки x 0 , y 0 , обязательно расположены на
одной прямой и перпендикулярны линиям уровней функций f  x, y  и g  x, y  .
Линией уровня функции полезности является линия безразличия, а линия уровня
функции связи совпадает с бюджетной прямой. Линии уровней функций f  x, y  и


g  x, y  , содержащие точку x 0 , y 0 , касаются в этой точке.




Градиент grad g x 0 , y 0 функции g  x, y  в точке x 0 , y 0 направлен вправо
вверх. Действительно,
g  p1 x  p2 y  I 

 p1 ,
x
x
g  p1 x  p2 y  I 

 p2 .
y
x
Поэтому








g x 0 , y 0  g x 0 , y 0 
grad g x , y 
i 
j  p1i  p2 j ,
x
y
0
0
а p1 и p 2 положительны по условию задачи.
56

1
0
x


Точно так же направлен градиент функции f  x, y  grad f x 0 , y 0 в точке
x
0

, y0 .
y
Áþäæåò í àÿ ï ðÿì àÿ p1x+p2 y=I
0
0
gr ad g(x ,y )
p2
0
0
gr ad f (x ,y )
0
0
(x ,y )
Ëèí èÿ áåçðàçëè÷èÿ
0
p1
Рис. 6
57
x
ЛЕКЦИЯ 8
Элементы теории игр в задачах оптимального управления
экономическими процессами.
Предмет теории игр. Основные понятия.
В условиях рыночной экономики возникают ситуации, в которых
сталкиваются интересы двух и более сторон. Такие ситуации относятся к
конфликтным.
Например,
взаимоотношения
между
поставщиком
и
потребителем, покупателем и продавцом, банком и клиентом. Для
конфликтных ситуаций оптимальность решений, принимаемых каждой из
сторон, существенно зависит от действий другой стороны. При этом ни одна
из сторон не может полностью контролировать положение, т.к. обеим
сторонам приходится принимать решение в условиях неопределенности.
Раздел математики, изучающий конфликтные ситуации на основе их
математических моделей, называется теорией игр.
Отметим основные ее понятия:
игра – упрощенная математическая модель конфликтной ситуации,
отличающаяся от реальной темы, что ведется по определенным правилам,
при этом каждый из участников принимает такие решения, которые, как он
полагает, обеспечат ему наилучший исход;
исход игры – значение некоторой функции, называемой функцией
выигрыша ли платежной функцией, которая может задаваться либо
аналитическим выражением, либо матрицей;
стратегия
–
совокупность
правил,
однозначно
определяющих
последовательность действий игрока в каждой конкретной ситуации.
Величина выигрыша зависит от стратегии игрока. Всякая игра состоит из
партий;
партией называют каждый вариант реализации игры. В партии игроки
совершают конкретные ходы;
58
ход – выбор и реализация игроком одного из допустимых вариантов
поведения.
Целью теории игр является определение оптимальной стратегии для
каждого игрока.
Игры можно классифицировать по разным признакам:
Например:
- по количеству стратегий игры делятся на конечные и бесконечные;
- по взаимоотношению участников на бескоалиционные (без права
заключения
соглашения),
некооперативные,
и
коалиционные
(кооперативные);
- по характеру выигрышей на игры с нулевой суммой (общий капитал
игроков не меняется, а лишь перераспределяется в ходе игры, при этом
сумма выигрышей равна 0, а проигрыш есть отрицательный выигрыш и с
ненулевой суммой;
- по виду платежной функции на матричные и непрерывные;
- по количеству ходов игры на одноходовые и многоходовые
(многоходовые
игры
подразделяются
на
стохастические
и
дифференциальные уравнения).
Ограничимся изучением парных матричных игр с нулевой суммой, а
именно таких игр, в которых у каждого из двух игроков А и В конечное
число возможных ходов – чистых стратегий.
Решение матричных игр в чистых стратегиях
Пусть у игроков А и В соответственно m и n чистых стратегий, которые
обозначим через Ai , i  1, m и B j , j  1, n .
Выбор игроками любой пары стратегий Ai и B j однозначно определяет
исход игры, описываемый числом aij . Матрица H  aij , i  1, m, j  1, n
называется платежной матрицей, где aij – выигрыш игрока А и проигрышь
 a  игрока В.
ij
59
Платежную матрицу удобно также представить в виде таблицы 5
Bj
B1
B2

Bn
a11
a12

a1n
A2
a21
a22

a2n





Am
a m1
am 2

am n
Ai
A1
В ее строках расположены чистые стратегии игрока А, а в столбцах –
чистые стратегии игрока В.
Цель матричной игры – выбор наиболее выгодных стратегий,
доставляющих игроку А максимальный выигрыш, а игроку В – минимальный
проигрыш. Стратегию игрока А называют оптимальной, если при ее
применении выигрыш игрока А не уменьшается при любой стратегии игрока
В. Оптимальной для игрока В называют стратегию, при которой проигрыш
игрока В не увеличивается при любой стратегии игрока А. При поиске
оптимальных стратегий игроки соблюдают принцип осторожности, согласно
которому противник является по меньшей мере таким же разумным и не
упустит ни единой возможности использовать любую ошибку соперника в
своих интересах. Пусть игрок А выбрал некоторую стартегию Ai . Сначала он


найдет минимальное значение ожидаемого выигрыша:  i  min aij j  1, m , а
j


затем из всех  i выберет наибольшее   min ai i  1, m .
i
Число  называют нижней ценой игры и является гарантированным
выигрышем игрока А.
Очевидно,  находится в одной из строк матрицы H, к примеру в
строке i0 . Тогда стратегию Ai 0 называют максиминной, т.к.   max (min aij ) .
i
60
j
В свою очередь игрок В, стремясь минимизировать проигрыш и
используя принцип осторожности, сначала для каждой чистой стратегии  j
найдет максимально возможный проигрыш –  j  max aij  j  1n  , а затем
i
j
среди
выберт
минимальное
соответствовать чистая стратегия
значение
  min  j .
j
Ему
будет
B j 0 , называемая минимаксной, т.к.
  min (max aij ) . Число  называют верхней ценой игры. Оно показывает
j
i
какой максимальный проигрыш может быть у игрока В. Таким образом,
правильно используя чистые стратегии, игрок А обеспечит выигрыш не
меньше , а игрок В не позволит игроку А выиграть больше чем .
Рассмотрим примеры нахождения  и  .
Пример 1. Пусть игра задана платежной матрицей 4  3 :
3 1

2 1
H 
5 7

4 8
0

4
6

2
Выпишем для каждой строки справа от матрицы min aij , а снизу max aij
j
каждого столбца. Тогда получим
3 1

2 1
5 7

4 8
5 8
0  1

4 1
6 5

2  2
6
  max min aij  max  1; 1; 5; 2  5
i
j
  min max aij  min 5; 8; 6  5
j
i
Верхняя и нижняя цены игры совпали:     5 .
61
i
Пример 2. Задана платежная матрица
4

H  0
5

5
7 10 1  1

3 2 6 0
4 9 8  4
7 10 8
  max  1; 0; 4  4
  min 5; 7; 10; 8  5
Здесь   4  5   .
Теорема 1. В любой матричной игре нижняя цена игры не превосходит
верхней цены игры, т.е.    .
Обозначим через i0 и j0 номера чистых стратегий, при котором    .
Пару чистых стратегий Ai 0 и B j 0 при этом называют седловой точкой
игры, а aij – седловым элементом платежной матрицы.
Число      называют чистой ценой игры. Простота решения игры
с седловой точкой заключается в том, что сразу найдены оптимальные
стратегии: максиминная Ai 0 для игрока А и минимаксная B j 0 для игрока В, а
цена игры – седловой элемент платежной матрицы:       ai 0 j 0 .
Отметим, что матричная игра может содержать несколько седловых точек.
Максиминные и минимаксные стратегии называют общим термином –
минимаксными стратегиями, а их выбор – принципом минимакса.
Решение матричных игр в смешанных стратегиях
Рассмотрим конечные матричные игры, в которых нет седловой точки,
т.е.    .
Нетрудно доказать, что    . Если игра одноходовая, то по принципу
минимакса игроку А гарантирован выйгрыш    , а игроку В – проигрыш
   . Таким образом, для цены игры  справедливо соотношение
62
   
(48)
Если игра повторяется неоднократно, то постоянный выбор игроками
минимаксных стратегий не логичен. Действительно, игрок В, зная что игрок
А применяет лишь минимаксную стратегию Ai 0 , выберет иную стратегию –
стратегию, соответствующую наименьшему элементу в строке i0 платежной
матрицы. Такие же рассуждения имеют место и для поведения игрока А.
Следовательно, при неоднократном повторении игры игрокам необходимо
менять стратегии. Выясним механизм выбора игроками оптимальных
стратегий, а также что принять за стоимость игры.
Рассмотрим матричную игру, заданную таблицей 6.
Таблица 6
Ai
Bj
pi
B1
B2

Bn
A1
a11
a12

a1n
p1
A2
a21
a22

a2n
p2






Am
a m1
am 2

am n
pm
qj
q1
q2

qn


Через pi i  1, m и q j
 j  1, n обозначим соответственно вероятности
(относительные частоты), согласно которым игроки А и В выбирают
стратегии Ai и B j .
Очевидно, что pi  0
m
i  1m ,  pi  1 ,
i 1


q j  0 j  1, n ,
n
 q j  1.
j 1
Упорядоченные множества p  ( p1 , p 2 ,, p m ) и q  (q1 , q1 ,..., q n ) полностью
63
определяет характер игры игроков А и В и называются их смешанными
стратегиями. Отметим, что любая их чистая стратегия Ai и B j может быть
описана
как
смешанная.
Действительно,
p  (0, ..., 0,1, 0, ..., 0)
или
q  (0, ..., 0,1, 0, ..., 0) .
Пусть игроки А и В применяют смешанные стратегии p и q, выбирают
их случайно. Тогда вероятность выбора комбинации Ai B j будет равна pi q j .
Игра приобрела случайный характер. Следовательно, случайной
становится и величина выигрыша.
Этой величиной является математическое ожидание выигрыша,
которое определяется формулой:
m
n
f ( p, q)   aij pi q j
i 1 j 1
Функцию f ( p, q) называют платежной функцией игры с заданной
матрицей. Как и выше, введем понятие нижней и верхней цены игры,
сохраняя при этом обозначения  и  :
  max min f ( p, q) ,   min max f ( p, q) .
p
q
q
p
Оптимальными смешанными стратегиями p  и q  называют такие
стратегии, при которых     f ( p  , q  ) . Величину f ( p  , q  ) называют
ценой игры v.
Для практических целей важны следующие свойства оптимальных
смешанных стратегий, выражаемые следующими теоремами.
Сформулируем основную теорему теории игр.
Теорема (Нейман): Любая конечная матричная игра имеет, по крайней
мере, одно оптимальное решение, возможно, среди смешанных стратегий.
Теорема 1. Для того чтобы смешанные стратегии p    p1 , p2 , , pm  и
q   q1 , q2 , , qm 
были
оптимальными,
выполнение неравенств
64
необходимо
и
достаточно
m
 aij pi  
i 1
n
 aij q j  
j 1
Теорема
2.
Пусть
 j  1, n
i  1, m
(49)
(50)
p    p1 , p2 , , pm 
и
q   q1 , q2 , , qm 
–
оптимальные смешанные стратегии и  – цена игры.




Только те вероятности pi , i  1, m , отличны от нуля, для которых
n
 aik qk   .
k 1
Только те вероятности qk , k  1, n , отличны от нуля, для которых
m
 aik pi   .
i 1
Методы решения матричных игр в смешанных стратегиях.
В этой лекции рассматриваются матричные игры, не имеющие
седловых точек.
2  2 – игры.
Рассмотрим игру с платежной матрицей
a12 
a

H   11
a
a
 21
22 
Пусть игрок A применяет набор своих оптимальных стратегий
p    p1 , p2  . По основной теореме теории игр это обеспечивает ему
выигрыш  при любых стратегиях игрока В, т.е. выполняются соотношения:
a11 p1  a21 p2  



a12 p1  a22 p2  
при стратегии В1 игрока В
при стратегии В2 игрока В
Дополняя их уравнением
p1  p2  1
(52)
65
(51)
получим систему линейных уравнений относительно p1 , p2 и  . Решая
ее найдем
p1 
a22  a21
a a
a a  a12a21
, p2  11 12 ,   11 22
, (53)
d
d
d
где d  a11  a22  a12  a21 .
Повторяя те же рассуждения для игрока В, получим систему линейных
уравнений
a11q1  a12 q 2  



a 21q1  a 22 q 2  
q   q   1
2
 1
(54)
Ее решениями будут
q1 
a22  a12
a  a21
a a  a12a21
, q2  11
,   11 22
,
d
d
d
(55)
Пример. Молокозавод поставляет в магазин молочную продукцию ( T1 )
и кисломолочную продукцию ( T2 ). Согласно договора между ними
продукция поступает в магазин два раза в день: с 10.00 до 11.00 (1-ый срок) и
с 17.00 до 18.00 (2-ой срок). Если молокозавод соблюдает сроки поставок, то
магазин выплачивает премии по следующей схеме: при поставке продукции
T1 в первый срок выплачивает 5 тыс. руб., во второй срок – 3 тыс. руб.; при
поставке продукции T2 в первый срок выплачивает 2 тыс. руб., во второй
срок – 3 тыс. руб. Определить оптимальные стратегии поставок и получения
продукции.
Решение. Примем молокозавод за игрока А, а магазин – за игрока В.
Составим платежную матрицу игры:
Сроки
Продукция
T1
T2
1-ый
срок
срок
5
2
или
66
2-ой
1
3
 5 1

H  
 2 3
Найдем
  max min aij  max 1; 2  2
j
i
  min max aij  min 5; 3  3 ,
j
i
   , седловой точки нет. Применим формулы (53) – (55) для
определения оптимальных стратегий и цены игры:
32 1
5 1 4
3 1 2
 , p2 
 , q1 
 ,
5
5
5
5
5
5
52 3
5  3  1  2 13
q2 
 , 
  2,6 ,
5
5
5
5
1 4
 2 3
Оптимальные стратегии: p    ;  , q    ;  , цена игры   2,6 .
5 5
 5 5
d  5  3  1  2  5 , p1 
Таким образом, молокозавод поставляет молочную продукцию с
вероятностью
1
4
, а кисломолочную продукцию – с вероятностью
, а
5
5
магазин получает продукцию в 1-ый срок с вероятностью
с вероятностью
2
, а во 2-ой срок –
5
3
и выплачивает 2,6 тыс. руб. премии молокозаводу
5
ежедневно.
Матричная
игра
2 2
допускает
простую
геометрическую
интерпретацию.
Нахождение цены игры  и оптимальной стратегии p  для игрока А
равносильно решению уравнения:
  min a1k p1  a2 k 1  p1   max min a1k p  a2 k 1  p 
1k 2
0 p 1 1k 2
(56)
Для нахождения правой части (56) применим графический метод.
67
Пусть игрок А выбрал смешанную стратегию p   p, 1  p , p  0; 1 , а
игрок В – k-ую чистую стратегию, k  1,2 . Тогда средний выигрыш игрока А
окажется равным
z  a11 p  a21 1  p  при стратегии B1
(57)
z  a12 p  a22 1  p  при стратегии B 2
(58)
Очевидно, min a1k p  a2 k 1  p   ломанная S 0 S1S 2 , которую называют
1k 2
нижней огибающей прямых I и II.
Нетрудно видеть, что max S 0 S1S 2  p1
0 p 1
Таким образом, верхняя точка нижней огибающей – S 1 определяет
оптимальную стратегию игрока А: p    p1 , 1  p1  и цену игры  .
Проиллюстрируем описанный графичексий метод на рассмотренной
 5 1
выше игре с платежной матрицей H  
 .
 2 3
На плоскости pOz построим две прямые, описываемые уравнениями:
z  5 p  21  p  и z  p  31  p  или z  3 p  2 (I) и z  3  2 p (II).
Решая систему уравнений
z  3 p  2

 z  3  2 p,
1
1
13
найдем 3 p  2  3  2 p , p  , z  3   2   2,6 .
5
5
5
1 4
Таким образом, имеем полученный выше ответ игры: p    ;  и
5 5
  2,6 .
Теперь покажем как графическим методом найти стратегии игрока В.
  max ai1q1  ai 2 1  q1   min max ai1q  ai 2 1  q  (59)
1i 2
0q 1 1i 2
68
Пусть игрок В выбрал смешанную стратегию q  q, 1  q  , q  0; 1, а
игрок А – i-ую чистую стратегию, i  1,2 . Тогда средний выигрыш игрока В
окажется равным
z  a11q  a12 1  q  при стратегии A1
(60)
z  a21q  a22 1  q  при стратегии A2
(61)
На плоскости qOz уравнения (60) и (61) описывают прямые III и IV
Очевидно,
max ai1q  ai 2 1  q   ломанная r0 r1r2 , которую называют
1i 2
верхней огибающей прямых III и IV.
Нетрудно видеть, что min r0 r1r2  q1
0q 1
Таким образом, нижняя точка верхней огибающей – r1 определяет
оптимальную стратегию игрока В: q   q1 , 1  q1  и цену игры  .
Для рассмотренной выше гры с матрицей H найдем стратегии игрока В.
На плоскости qOz построим две прямые, описываемые уравнениями:
z  5q  1  q и z  2q  31  q  или z  4q  1 (III) и z  3  q (IV).
Решая систему уравнений
 z  4q  1

 z  3  q,
2
2
13
, z  4   1   2,6 .
5
5
5
 2 3
Таким образом, имеем q    ;  и   2,6 .
 5 5
найдем 4q  1  3  q , q 
Замечания. На практике оптимальную стратегию игрока В, если
оптимальная стратегия игрока А, следовательно, и цена игры известны,
находят приравниванием любого из двух средних выйгрышей игрока В к
цене игры:
a11q  a12 1  q    или a21q  a212 1  q    .
Для рассмотренного примера такими уравнениями будут
69
5  q  1  1  q  
13
5
8
2
4q  , q 
5
5
13
5
13
2
 q   3, q 
5
5
2  q  3  1  q  
или
Аналогично находят оптимальную стратегию игрока А, если известна
оптимальная стратегия игрока В.
2  n и m  2 – игры.
Решают такие игры графическим способом, описанным выше. Отличие
от 2  2 – игр заключается в следующем.
1) Нижняя (верхняя) огибающая семейства прямых
z  a1k p  a2 k 1  p , k  1, n
z  a q  a
i1
i2
1  q ,
i  1, m

содержит большее число отрезков.
2) Пусть в игре
2 n
в верхней
точке
нижней огибающей
пересекаются прямые k  k1 и k  k 2 . Тогда при нахождении оптимальной
смешанной стратегии игрока В согласно Теореме 2 полагают, что qk1  q ,
qk2  1  q , qk  0 , k  k1 , k 2 , где q – решение уравнения
a1k1 q  a1k2 1  q   
или
3) Пусть в игре
m2
a2 k1 q  a2 k2 1  q   
в нижней точке верхней огибающей
пересекаются прямые i  i1 и i  i2 . Тогда при нахождении оптимальной
смешанной стратегии игрока А согласно Теореме 2 полагают, что pi1  p ,
pi2 1  p , pi  0 , i  i1 , i2 , где p – решение уравнения
a1i1 p  a1i2 1  p   
или
a2i1 p  a2i2 1  p    .
m  n – игры.
При решении таких игр рекомендуется предварительно уменьшить
размеры платежной матрицы или упростить ее в некотором смысле. С этой
целью применяют следующие правила.
70
Правило доминировнаия.
Из платежной матрицы исключают чистые стратегии заведомо
невыгодные по сравнению с другими:
а) для
игрока
А
такими
стратегиями
являются
те,
которым
соответствуют строки с элементами не большими по сравнению с
элементами других строк;
б) для игрока В такими стратегиями являются те, которым
соответствуют столбцы с элементами не меньшими по сравнению с
элементами других столбцов.
Например, рассмотрим игру с матрицей
2

1
H 
5

5
5 8 3

4 2 3
6 1 1

6 1 1 
Сравнивая строки, убеждаемся, что элементы 2-ой строки не больше
соответствующих элементов 1-ой строки, а 3-ья строка совпадает с 4-ой.
Следовательно, стратегии A2 и A4 невыгодные и могут быть отброшены.
Матрица игры преобразуется к матрице
 2 5 8 3


 5 6 1 1
Сравнивая столбцы полученной матрицы, убеждаемся, что элементы 2го столбца не меньше соответствующих элементов 1-го столбца, а элементы
3-го столбца не меньше соответствующих элементов 4-го столбца, т.е.
стратегии B 2 и B3 также могут быть отброшены. Окончательно усеченная
матрица игры имеет вид
 2 3
 .
H1  
5
1


71
Таким образом, оптимальными стратегиями игроков А и В игры с
матрицей Н будут p    p1 , 0, p3 , 0 и q   q1 , 0, 0, q4 , где  p1 , p3  и q1 , q4 
– оптимальные стратегии игры с матрицей H 1 .
Аффинное правило.
Пусть p  и q  – оптимальные смешанные стратегии игроков А и В в
игре с платежной матрицей H  aij , m  n и ценой  . Тогда p  и q  будут
оптимальными стратегиями и в игре с матрицей H1   aij  c m n и ценой
 1    c .
 26 41 


Например, игру с матрицей H 1   29 23  можно заменить игрой с
 32 20 


2 7


матрицей H   3 1  , т.к. элементы этих матриц связаны соотношениями
 4 0


b
ij
 3  aij  20 : 26  3  2  20 ; 41  3  7  20 ; 29  3  3  20 ; 23  3  1  20 ;
32  3  4  20 ;
20  3  0  20 .
При
этом
оптимальные
стратегии
игр
совпадают, а цены игр связаны соотношением  1  3   20 .
В общем случае решение игр размера m  n в смешанных стратегиях
сводят к решению двух возможно двойственных ЗЛП. Изучению этого
вопроса посвящена следующая лекция.
72
ЛЕКЦИЯ 9
Методы решения матричных игр в смешанных стратегиях.
В этой лекции рассматриваются матричные игры, не имеющие
седловых точек.
2  2 – игры.
Рассмотрим игру с платежной матрицей
a12 
a

H   11
a
a
 21
22 
Пусть игрок A применяет набор своих оптимальных стратегий
p    p1 , p2  . По основной теореме теории игр это обеспечивает ему
выигрыш  при любых стратегиях игрока В, т.е. выполняются соотношения:
a11 p1  a21 p2  



a12 p1  a22 p2  
при стратегии В1 игрока В
при стратегии В2 игрока В
(62)
Дополняя их уравнением
p1  p2  1
(63)
получим систему линейных уравнений относительно p1 , p2 и  . Решая
ее найдем
p1 
a22  a21
a a
a a  a12a21
, p2  11 12 ,   11 22
,
d
d
d
(64)
где d  a11  a22  a12  a21 .
Повторяя те же рассуждения для игрока В, получим систему линейных
уравнений
73
a11q1  a12 q 2  



a 21q1  a 22 q 2  
q   q   1
2
 1
(65)
Ее решениями будут
q1 
a22  a12
a  a21
a a  a12a21
, q2  11
,   11 22
,
d
d
d
(66)
Пример. Молокозавод поставляет в магазин молочную продукцию ( T1 )
и кисломолочную продукцию ( T2 ). Согласно договора между ними
продукция поступает в магазин два раза в день: с 10.00 до 11.00 (1-ый срок) и
с 17.00 до 18.00 (2-ой срок). Если молокозавод соблюдает сроки поставок, то
магазин выплачивает премии по следующей схеме: при поставке продукции
T1 в первый срок выплачивает 5 тыс. руб., во второй срок – 3 тыс. руб.; при
поставке продукции T2 в первый срок выплачивает 2 тыс. руб., во второй
срок – 3 тыс. руб. Определить оптимальные стратегии поставок и получения
продукции.
Решение. Примем молокозавод за игрока А, а магазин – за игрока В.
Составим платежную матрицу игры:
Сроки
1-ый
Продукция
T1
T2
срок
 5 1

H  
2
3


Найдем
  max min aij  max 1; 2  2
i
j
j
i
срок
5
2
или
  min max aij  min 5; 3  3 ,
74
2-ой
1
3
   , седловой точки нет. Применим формулы (63) – (65) для
определения оптимальных стратегий и цены игры:
32 1
5 1 4
3 1 2
 , p2 
 , q1 
 ,
5
5
5
5
5
5
52 3
5  3  1  2 13
q2 
 , 
  2,6 ,
5
5
5
5
d  5  3  1  2  5 , p1 
1 4
 2 3
Оптимальные стратегии: p    ;  , q    ;  , цена игры   2,6 .
5 5
 5 5
Таким образом, молокозавод поставляет молочную продукцию с
вероятностью
1
4
, а кисломолочную продукцию – с вероятностью
, а
5
5
магазин получает продукцию в 1-ый срок с вероятностью
с вероятностью
2
, а во 2-ой срок –
5
3
и выплачивает 2,6 тыс. руб. премии молокозаводу
5
ежедневно.
Матричная
игра
2 2
допускает
простую
геометрическую
интерпретацию.
Нахождение цены игры  и оптимальной стратегии p  для игрока А
равносильно решению уравнения:
  min a1k p1  a2 k 1  p1   max min a1k p  a2 k 1  p 
1k 2
0 p 1 1k 2
(66)
Для нахождения правой части (66) применим графический метод.
Пусть игрок А выбрал смешанную стратегию p   p, 1  p , p  0; 1 , а
игрок В – k-ую чистую стратегию, k  1,2 . Тогда средний выигрыш игрока А
окажется равным
z  a11 p  a21 1  p  при стратегии B1
(67)
z  a12 p  a22 1  p  при стратегии B 2
(68)
75
Очевидно, min a1k p  a2 k 1  p   ломанная S 0 S1S 2 , которую называют
1k 2
нижней огибающей прямых I и II.
Нетрудно видеть, что
max S 0 S1 S 2  p1
0 p 1
Таким образом, верхняя точка нижней огибающей – S 1 определяет
оптимальную стратегию игрока А: p    p1 , 1  p1  и цену игры  .
Проиллюстрируем описанный графичексий метод на рассмотренной
 5 1
выше игре с платежной матрицей H  
 .
 2 3
На плоскости pOz построим две прямые, описываемые уравнениями:
z  5 p  21  p  и z  p  31  p  или z  3 p  2 (I) и z  3  2 p (II).
Решая систему уравнений
z  3 p  2

 z  3  2 p,
1
1
13
найдем 3 p  2  3  2 p , p  , z  3   2   2,6 .
5
5
5
1 4
Таким образом, имеем полученный выше ответ игры: p    ;  и
5 5
  2,6 .
Теперь покажем как графическим методом найти стратегии игрока В.
  max ai1q1  ai 2 1  q1   min max ai1q  ai 2 1  q 
1i 2
0q 1 1i 2
(69)
Пусть игрок В выбрал смешанную стратегию q  q, 1  q  , q  0; 1, а
игрок А – i-ую чистую стратегию, i  1,2 . Тогда средний выигрыш игрока В
окажется равным
z  a11q  a12 1  q  при стратегии A1
76
(70)
z  a21q  a22 1  q  при стратегии A2
Очевидно,
(71)
max ai1q  ai 2 1  q   ломанная r0 r1r2 , которую называют
1i 2
верхней огибающей прямых III и IV.
Нетрудно видеть, что
min r0 r1r2  q1
0q 1
Таким образом, нижняя точка верхней огибающей – r1 определяет
оптимальную стратегию игрока В: q   q1 , 1  q1  и цену игры  .
Для рассмотренной выше гры с матрицей H найдем стратегии игрока В.
На плоскости qOz построим две прямые, описываемые уравнениями:
z  5q  1  q и z  2q  31  q  или z  4q  1 (III) и z  3  q (IV).
Решая систему уравнений
 z  4q  1

 z  3  q,
найдем 4q  1  3  q , q 
2
2
13
, z  4   1   2,6 .
5
5
5
 2 3
Таким образом, имеем q    ;  и   2,6 .
 5 5
Замечания. На практике оптимальную стратегию игрока В, если
оптимальная стратегия игрока А, следовательно, и цена игры известны,
находят приравниванием любого из двух средних выйгрышей игрока В к
цене игры:
a11q  a12 1  q    или a21q  a212 1  q    .
Для рассмотренного примера такими уравнениями будут
5  q  1  1  q  
8
2
4q  , q 
5
5
13
5
13
5
13
2
 q   3, q 
5
5
2  q  3  1  q  
или
77
Аналогично находят оптимальную стратегию игрока А, если известна
оптимальная стратегия игрока В.
2  n и m  2 – игры.
Решают такие игры графическим способом, описанным выше. Отличие
от 2  2 – игр заключается в следующем.
4) Нижняя (верхняя) огибающая семейства прямых
z  a q  a
z  a1k p  a2 k 1  p , k  1, n
i1
i2
1  q ,
i  1, m

содержит большее число отрезков.
5) Пусть в игре
2 n
в верхней
точке
нижней огибающей
пересекаются прямые k  k1 и k  k 2 . Тогда при нахождении оптимальной
смешанной стратегии игрока В полагают, что qk1  q , qk2  1  q , qk  0 ,
k  k1 , k 2 , где q – решение уравнения
a1k1 q  a1k2 1  q   
или
6) Пусть в игре
m2
a2 k1 q  a2 k2 1  q   
в нижней точке верхней огибающей
пересекаются прямые i  i1 и i  i2 . Тогда при нахождении оптимальной
смешанной стратегии игрока А полагают, что pi1  p , pi2 1  p , pi  0 ,
i  i1 , i2 , где p – решение уравнения
a1i1 p  a1i2 1  p   
или
a2i1 p  a2i2 1  p    .
m  n – игры.
При решении таких игр рекомендуется предварительно уменьшить
размеры платежной матрицы или упростить ее в некотором смысле. С этой
целью применяют следующие правила.
Правило доминировнаия.
Из платежной матрицы исключают чистые стратегии заведомо
невыгодные по сравнению с другими:
78
а) для
игрока
А
такими
стратегиями
являются
те,
которым
соответствуют строки с элементами не большими по сравнению с
элементами других строк;
б) для игрока В такими стратегиями являются те, которым
соответствуют столбцы с элементами не меньшими по сравнению с
элементами других столбцов.
Например, рассмотрим игру с матрицей
2

1
H 
5

5
5 8 3

4 2 3
6 1 1

6 1 1 
Сравнивая строки, убеждаемся, что элементы 2-ой строки не больше
соответствующих элементов 1-ой строки, а 3-ья строка совпадает с 4-ой.
Следовательно, стратегии A2 и A4 невыгодные и могут быть отброшены.
Матрица игры преобразуется к матрице
 2 5 8 3


 5 6 1 1
Сравнивая столбцы полученной матрицы, убеждаемся, что элементы 2го столбца не меньше соответствующих элементов 1-го столбца, а элементы
3-го столбца не меньше соответствующих элементов 4-го столбца, т.е.
стратегии B 2 и B3 также могут быть отброшены. Окончательно усеченная
матрица игры имеет вид
 2 3
 .
H1  
 5 1
Таким образом, оптимальными стратегиями игроков А и В игры с
матрицей Н будут p    p1 , 0, p3 , 0 и q   q1 , 0, 0, q4 , где  p1 , p3  и q1 , q4 
– оптимальные стратегии игры с матрицей H 1 .
79
Аффинное правило.
Пусть p  и q  – оптимальные смешанные стратегии игроков А и В в
игре с платежной матрицей H  aij , m  n и ценой  . Тогда p  и q  будут
оптимальными стратегиями и в игре с матрицей H1   aij  c m n и ценой
 1    c .
 26 41 


Например, игру с матрицей H 1   29 23  можно заменить игрой с
 32 20 


2 7


матрицей H   3 1  , т.к. элементы этих матриц связаны соотношениями
 4 0


b
ij
 3  aij  20 : 26  3  2  20 ; 41  3  7  20 ; 29  3  3  20 ; 23  3  1  20 ;
32  3  4  20 ;
20  3  0  20 .
При
этом
оптимальные
стратегии
игр
совпадают, а цены игр связаны соотношением  1  3   20 .
В общем случае решение игр размера m  n в смешанных стратегиях
сводят к решению двух возможно двойственных ЗЛП.
Редукция матричных игр к ЗЛП.
Пусть игра m  n задана платежной матрицей H  aij , i  1, m, j  1, n .
Через p    p1 , p2 , , pm  и q   q1 , q2 , , qn  обозначим соответственно
оптимальные стратегии игроков А и В. Пусть  – цена игры. Не умаляя
общности, полагаем   0 . В противном случае с помощью аффинного
правила добьемся того, что все aij  0 .
Оптимальная стратегия стратегия игрока А обеспечивает ему средний
выигрыш, не меньший  , при любой стратегии игрока В. Поэтому все
средние выигрыши игрока А можно выписать в виде системы неравенств:
80
a11 p1  a21 p2    am1 pm  
a p  a p    a p  
 12 1
22 2
m2 m

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .
a1n p1  a2 n p2    am n pm  
(72)
Введем новые переменные:
x1 
p1

, x2 
p2

, , xm 
pm

(73)
,
Тогда после деления каждого неравенства из (71) на  получим новую
систему неравенств
a11 x1  a21 x2    am1 xm  1
a x  a x    a x  1
 12 1
22 2
m2 m

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .
a1n x1  a2 n x2    am n xm  1
(73)
Из равенства
p1  p2    pm  1
нетрудно получить соотношение для xi , i  1, m :
1
x1  x2    xm  .

Игрок А стремится максимизировать свой гарантированный выигрыш
 . Максимизация  равносильна минимизации
1

. Следовательно, получили
следующую задачу для нахождения оптимальной стратегии игрока А:
  x1  x2    xm  min
(74)
при условиях (73) и
xi  0, i  1, m
(75)
Сформулированная задача (74) – (76) является ЗЛП.
81
Повторим с естественными изменениями предыдущие рассуждения для
определения оптимальной стратегии игрока В.
Игрок В стремиться минимизировать гарантированный проигрыш  .
Все средние проигрыши игрока В запишем в виде системы неравенст:
a11q1  a12q2    a1n qn  
a q  a q    a q  
 21 1
22 2
2n n
,

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.

am1q1  am 2 q2    am nqn  
(76)
которые следуют из того, что средний проигрыш игрока В не
превосходит цены игры  при любой стратегии игрока А.
В обозначениях
z1 
q1

, z2 
q2

, , z n 
qn

система неравенств (76) примет вид
a11 z1  a12 z 2    a1n xn  1
a z  a z    a z  1
 21 1
22 2
2n n

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .
am1 z1  am 2 z 2    am n z n  1
(77)
Применение z j , j  1, n удовлетворяют соотношению
1
z1  z 2    z n  .

Минимизация
1

равносильна максимизации  .
Получили следующую задачу для нахождения оптимальной стратегии
игрока В:
f  z1  z 2    z n  max
при условиях (77) и
82
(78)
z j  0, j  1, n
(79)
Задача (77) – (79) также является ЗЛП.
Таким образом, игра m  n свелась к двум ЗЛП, которые запишем в
матричном виде
H T Z  C

Z  0
  B T Z  min

I 
 HX  B

X  0
 f  C T X  max

II
 x1 
 z1 
 1
 1
 
 
 
 
 x2 
 z2 
 1
 1
X   , Z   , B  , C  




 
 
 
 
1 m 1
 1  n 1
 x m  m 1
 z n  n 1
Очевидно, задачи I и II являются двойственными ЗЛП.
83
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. А.В. Соколов, В.В. Токарев. Методы оптимальных решений. Т.1.
Общие положения. Математическое программирование. Москва:
ФИЗМАТЛИТ, 2010.
2. А.В. Соколов, В.В. Токарев. Методы оптимальных решений. Т.2.
Многокритериальность.
Динамика.
Неопределенность.
Москва:
ФИЗМАТЛИТ, 2010.
3. Конюховский П.В. Математические методы исследования операций в
экономике. СПб.: Питер, 2000.
4. М.
Интрилигатор. Математические
методы
оптимизации
экономическая теория. М.: Изд. Айрис-Пресс, 2002.
5. Ф.П. Васильев. Методы оптимизации. М. Факториал Пресс, 2005.
84
и
ОГЛАВЛЕНИЕ
Введение ……………………………………………………………………..
3
ЛЕКЦИЯ 1. Исследование операций. Экономико-математические
модели. ……………………………………………………………………….
4
ЛЕКЦИЯ 2. Балансовые модели. Модель Леонтьева многоотраслевой
экономики. Продуктивные модели………………………………………….
8
ЛЕКЦИЯ 3,4,5. Задачи математического и линейного
программирования. Модели линейного программирования……………...
15
ЛЕКЦИЯ 6. Динамическое программирование. Принцип оптимальности
и функциональности. Функциональное уравнение Беллмана…………….
40
ЛЕКЦИЯ 7. Модели потребительского выбора. Функция полезности.
Линии безразличия. Оптимизация функции полезности. Функции
спроса и предложения……………………………………………………….
49
ЛЕКЦИЯ 8. Элементы теории игр в задачах оптимального управления
экономическими процессами……………………………………………….
58
ЛЕКЦИЯ 9. Методы решения матричных игр в смешанных стратегиях...
73
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ ……………………………
84
85
Учебное издание
Г. Н. Камышова,
Н. Н. Терехова
МЕТОДЫ ОПТИМАЛЬНЫХ
РЕШЕНИЙ
Краткий курс лекций
Издается в авторской редакции
Корректура авторов
86