Домашнее задание по графам для 11-3 и 11

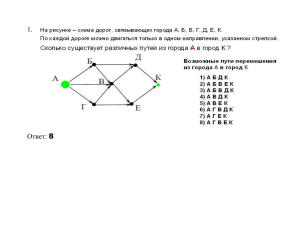
Практическая работа «Графы»
1. Нарисовать взвешенный связный граф, содержащий 6 вершин и 8 ребер.
o Составить матрицу смежности с учетов весов ребер.
o Определить вершину с максимальной степенью.
o Нарисовать подграф, остовной связный подграф, произвольное остовное связное
дерево для этого графа.
o Построить по алгоритму Крускала остовное связное дерево минимального веса для
этого графа, вычислить цикломатическое число, подсчитать минимальный вес
дерева.
2. По матрице смежности построить схему графа.
A
B
C
D
Е
A B C DЕ
1
4 1
4 42
1 4
12
3. В таблице приведена стоимость перевозок между соседними железнодорожными
станциями. Укажите схему, соответствующую таблице.
A
A
B
C
D
1)
B
4
4
C
3
D
5
6
3
6
5
2)
3)
4)
4. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на
пересечениях строк и столбцов таблиц, означают стоимость проезда между
соответствующими соседними станциями. Если пересечение строки и столбца пусто, то
станции не являются соседними.
Укажите таблицу, для которой выполняется условие: “Минимальная стоимость проезда
из А в B не больше 6”.
Стоимость проезда по маршруту складывается из стоимостей проезда между
соответствующими соседними станциями.
1)
2)
3)
4)
A
A
B
C
D
Е
3
1
B C D Е
3 1
4
2
4
2
2
2
A
A
B
C
D
Е
3
1
1
B C D Е
3 1 1
4
4
2
2
A
A
B
C
D
Е
3
1
B C D Е
3 1
4
1
4
2
1
2
A
A
B
C
D
Е
1
B C D Е
1
4
1
4
4 2
4
1 2
5. Грунтовая дорога проходит последовательно через населенные пункты А, B, С и D.
При этом длина дороги между А и В равна 80 км, между В и С -50 км, и между С и D 10 км. Между А и С построили новое асфальтовое шоссе длиной 40 км. Оцените
минимально возможное время движения велосипедиста из пункта А в пункт В, если
его скорость по грунтовой дороге - 20 км/час, по шоссе - 40 км/час.
1) 1 час
2) 1,5 часа
3) 3,5 часа
4) 4 часа
6. Построить по алгоритму Крускала остовное связное дерево минимального веса для
заданного графа, вычислить цикломатическое число, подсчитать минимальный вес
дерева.
20
4
3
7
20
25
15
30
35
2
5
40
30
10
32
15
25
10
8
6
30
1