КДР 11-3 май итоговая

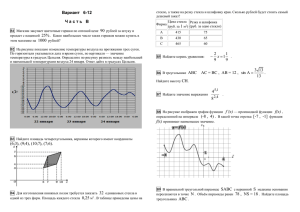
Инструкция
по проведению контрольной диагностической работы (КДР) № 3
(итоговая) по математике в 11 классе
Повторение программы средней школы по математике 5 – 11 классы.
Цель:
-отследить уровень усвоения учащимися основных тем школьного курса по математике
5 – 11;
- итоговая проверка готовности учащихся к ЕГЭ 2012 года по математике.
Задачи:
1. Планомерная подготовка учащихся к написанию ЕГЭ.
2. Проявление пробелов в знаниях учащихся, с целью дальнейшего их устранения.
3. Ознакомление учащихся с особенностями ЕГЭ по математике.
4. Психологическая подготовка к ЕГЭ.
О проведении работы:
1. Работа состоит из 2 частей: 1 часть (задания В1 – В14) – базовый
(общеобразовательный) уровень, задания формулируются на языке ЕГЭ, 2 часть (С1 – С6)
состоит из заданий аналогичных тем, которые раньше требовались при поступлении в
технические ВУЗы.
Используемые материалы при составлении работы: задания открытого банка (mathege.ru)
и задания различных сборников по подготовке к поступлению во ВТУЗы, а также
разработки ФИПИ и др..
2. Время написания работы: на усмотрение администрации ОУ и учителей математики,
работающие в 11 классах, но не менее 90 минут и не более 240 минут.
Вариант 1
Часть 1
Ответом в заданиях первой части является целое число или конечная десятичная дробь
В1. Мобильный телефон стоил 2200 рублей. Через некоторое время цену на эту модель
снизили до 1650 рублей. На сколько процентов была снижена цена?
В2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По
горизонтали указывается дата и время суток, по вертикали — значение температуры в
градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей
температурами воздуха 28 мая. Ответ дайте в градусах Цельсия.
В3. Найдите площадь ромба, изображенного на рисунке.
В4. Телефонная компания предоставляет на выбор три тарифных плана.
Тарифный план
Абонентская плата
Плата за 1 минуту разговора
Повременный
135 руб. в месяц
0,3 руб.
Комбинированный
255 руб. за 450 мин. в месяц 0,28 руб. за 1 мин. сверх 450 мин. в
месяц.
Безлимитный
380 руб. в месяц
Абонент выбрал наиболее дешевый тарифный план исходя из предположения, что общая
длительность телефонных разговоров составляет 650 минут в месяц. Какую сумму он
должен заплатить за месяц, если общая длительность разговоров в этом месяце
действительно будет равна 650 минутам? Ответ дайте в рублях.
В5. Решите уравнение
.
В6. Угол C треугольника ABC, вписанного в окружность радиуса 36, равен 30°. Найдите
сторону AB этого треугольника.
В7. Найдите
, если
.
В8.
В9. В правильной четырехугольной пирамиде
вершина,
,
. Найдите длину отрезка
точка
.
— центр основания,
В10. На семинар приехали 3 ученых из Швейцарии, 5 из Голландии и 4 из Франции.
Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что шестым
окажется доклад ученого из Швейцарии.
В11. Объем первого цилиндра равен 81 м3. У второго цилиндра высота в 4 раза больше, а
радиус основания — в 3 раза меньше, чем у первого. Найдите объем второго цилиндра.
Ответ дайте в кубических метрах.
В12. Высота над землeй подброшенного вверх мяча меняется по закону
, где h — высота в метрах, t — время в секундах, прошедшее с
момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
В13. Два мотоциклиста стартуют одновременно в одном направлении из двух
диаметрально противоположных точек круговой трассы, длина которой равна 22 км.
Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из
них на 20 км/ч больше скорости другого?
В14. Найдите наименьшее значение функции
на отрезке
.
Часть 2
Задания второй части выполняются с подробным решением и записью ответа.
С1. а) Решите уравнение sin x  1  2 cos 2x ; б) Найдите корни принадлежащие отрезку
  
 2 ;   .
С2. Дан куб ABCDA1B1C1D1 . Найдите угол между плоскостями AB1D1 и ACD1.
x
x
x 1
2 x 1

0
9  11  2  3  2
С3. Решите систему неравенств 
.
2



log
5
x

x

2
 x 1
С4. Расстояние между параллельными прямыми равно 12. На одной из них лежит точка C
, а на другой – точки A и B , причем треугольник ABC –равнобедренный и его боковая
сторона равна 13. Найдите радиус окружности, вписанной в треугольник ABC.
С5. Найдите все значения a , при которых функция f  x   x 2  x  a 2  5 x имеет более
двух точек экстремума.
С6. Найдите все тройки натуральных чисел k, m и n , удовлетворяющие уравнению 2⋅ k !=
m! − 2⋅n! (1!=1; 2!=1⋅2 = 2; n!=1⋅2⋅...⋅n) .
Вариант 2
Часть 1
Ответом в заданиях первой части является целое число или конечная десятичная дробь
В1. Мобильный телефон стоил 7500 рублей. Через некоторое время цену на эту модель
снизили до 4200 рублей. На сколько процентов была снижена цена?
В2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По
горизонтали указывается дата и время суток, по вертикали — значение температуры в
градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей
температурами воздуха 7 августа. Ответ дайте в градусах Цельсия.
В3. Найдите площадь прямоугольника, изображенного на рисунке.
В4. Телефонная компания предоставляет на выбор три тарифных плана.
Тарифный план
Абонентская плата
Плата за 1 минуту разговора
Повременный
Нет
0,25 руб.
Комбинированный
130 руб. за 320 мин. в месяц 0,2 руб. за 1 мин. сверх 320 мин. в
месяц.
Безлимитный
200 руб. в месяц
Абонент выбрал наиболее дешевый тарифный план исходя из предположения, что общая
длительность телефонных разговоров составляет 900 минут в месяц. Какую сумму он
должен заплатить за месяц, если общая длительность разговоров в этом месяце
действительно будет равна 900 минутам? Ответ дайте в рублях.
В5. Решите уравнение
.
В6. Сторона AB треугольника ABC равна 7. Противолежащий ей угол C равен 150°.
Найдите радиус окружности, описанной около этого треугольника.
В7. Найдите
В8.
, если
.
В9. В правильной четырехугольной пирамиде
вершина,
,
. Найдите длину отрезка
точка
.
— центр основания,
В10. На семинар приехали 4 ученых из Норвегии, 6 из России и 6 из Великобритании.
Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что вторым
окажется доклад ученого из Норвегии.
В11. Объем первого цилиндра равен 94 м3. У второго цилиндра высота в 3 раза больше, а
радиус основания — в 2 раза меньше, чем у первого. Найдите объем второго цилиндра.
Ответ дайте в кубических метрах.
В12. Высота над землeй подброшенного вверх мяча меняется по закону
, где h — высота в метрах, t — время в секундах, прошедшее с
момента броска. Сколько секунд мяч будет находиться на высоте не менее 4 метров?
В13. Два мотоциклиста стартуют одновременно в одном направлении из двух
диаметрально противоположных точек круговой трассы, длина которой равна 19 км.
Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из
них на 15 км/ч больше скорости другого?
В14. Найдите наибольшее значение функции
на отрезке
.
Часть 2
Задания второй части выполняются с подробным решением и записью ответа.
С1. а) Решите уравнение sin 2x  cos 4x ; б) Найдите корни принадлежащие отрезку


  ; 2  .
С2. Дан куб ABCDA1B1C1D1 . Длина ребра куба равна 1. Найдите расстояние от вершины
A1 до плоскости AB1D1 .
x
x
x

3  16  2  81  5  36
С3. Решите неравенство 
.
2
log
3
x

x

2

 1 x 


С4. Расстояние между параллельными прямыми равно 4. На одной из них лежит точка C ,
а на другой – точки A и B , причем треугольник ABC –равнобедренный и его боковая
сторона равна 5. Найдите радиус окружности, вписанной в треугольник ABC.
С5. Найдите все значения a , при которых функция f  x   x 2  4 x  a 2  6 x имеет хотя бы
одну точку максимума.
С6. Найдите все тройки натуральных чисел k, m и n , удовлетворяющие уравнению 2⋅ k !=
m! − 2⋅n! (1!=1; 2!=1⋅2 = 2; n!=1⋅2⋅...⋅n) .
Вариант 3
Часть 1
Ответом в заданиях первой части является целое число или конечная десятичная дробь
В1. Мобильный телефон стоил 2500 рублей. Через некоторое время цену на эту модель
снизили до 1550 рублей. На сколько процентов была снижена цена?
В2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По
горизонтали указывается дата и время суток, по вертикали — значение температуры в
градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей
температурами воздуха 9 августа. Ответ дайте в градусах Цельсия.
В3. Найдите площадь ромба, изображенного на рисунке.
В4. Телефонная компания предоставляет на выбор три тарифных плана.
Тарифный план
Абонентская плата
Плата за 1 минуту разговора
Повременный
Нет
0,4 руб.
Комбинированный 180 руб. за 400 мин. в месяц 0,3 руб. за 1 мин. сверх 400 мин. в
месяц.
Безлимитный
245 руб. в месяц
Абонент выбрал наиболее дешевый тарифный план исходя из предположения, что общая
длительность телефонных разговоров составляет 500 минут в месяц. Какую сумму он
должен заплатить за месяц, если общая длительность разговоров в этом месяце
действительно будет равна 500 минутам? Ответ дайте в рублях.
В5. Решите уравнение
.
В6. Угол C треугольника ABC, вписанного в окружность радиуса 43, равен 30°. Найдите
сторону AB этого треугольника.
В7. Найдите
, если
.
В8.
В9. В правильной четырехугольной пирамиде
точка
вершина,
,
. Найдите длину отрезка
.
— центр основания,
В10. На семинар приехали 6 ученых из Швейцарии, 3 из Болгарии и 6 из Австрии.
Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что третьим
окажется доклад ученого из Болгарии.
В11. Объем первого цилиндра равен 48 м3. У второго цилиндра высота в 3 раза больше, а
радиус основания — в 4 раза меньше, чем у первого. Найдите объем второго цилиндра.
Ответ дайте в кубических метрах.
В12. Высота над землeй подброшенного вверх мяча меняется по закону
, где h — высота в метрах, t — время в секундах, прошедшее с
момента броска. Сколько секунд мяч будет находиться на высоте не менее 5 метров?
В13. Два мотоциклиста стартуют одновременно в одном направлении из двух
диаметрально противоположных точек круговой трассы, длина которой равна 7 км. Через
сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 5
км/ч больше скорости другого?
В14. Найдите наименьшее значение функции
на отрезке
Часть 2
Задания второй части выполняются с подробным решением и записью ответа.
С1. а) Решите уравнение sin x  1  2 cos 2x ; б) Найдите корни принадлежащие отрезку
  
 2 ;   .
С2. Дан куб ABCDA1B1C1D1 . Найдите угол между плоскостями AB1D1 и ACD1.
.
x
x
x 1
2 x 1

0
9  11  2  3  2
С3. Решите систему неравенств 
.
2

log x 1 5 x  x  2


С4. Расстояние между параллельными прямыми равно 12. На одной из них лежит точка C
, а на другой – точки A и B , причем треугольник ABC –равнобедренный и его боковая
сторона равна 13. Найдите радиус окружности, вписанной в треугольник ABC.
С5. Найдите все значения a , при которых функция f  x   x 2  x  a 2  5 x имеет более
двух точек экстремума.
С6. Найдите все тройки натуральных чисел k, m и n , удовлетворяющие уравнению 2⋅ k !=
m! − 2⋅n! (1!=1; 2!=1⋅2 = 2; n!=1⋅2⋅...⋅n) .
Вариант 4
Часть 1
Ответом в заданиях первой части является целое число или конечная десятичная дробь
В1. Мобильный телефон стоил 8000 рублей. Через некоторое время цену на эту модель
снизили до 7600 рублей. На сколько процентов была снижена цена?
В2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По
горизонтали указывается дата и время суток, по вертикали — значение температуры в
градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей
температурами воздуха 19 февраля. Ответ дайте в градусах Цельсия.
В3. Найдите площадь ромба, изображенного на рисунке.
В4. Телефонная компания предоставляет на выбор три тарифных плана.
Тарифный план
Абонентская плата
Плата за 1 минуту разговора
Повременный
135 руб. в месяц
0,3 руб.
Комбинированный 255 руб. за 450 мин. в месяц
0,28 руб. за 1 мин. сверх 450 мин. в
месяц
Безлимитный
380 руб. в месяц
Абонент выбрал наиболее дешевый тарифный план исходя из предположения, что общая
длительность телефонных разговоров составляет 400 минут в месяц. Какую сумму он
должен заплатить за месяц, если общая длительность разговоров в этом месяце
действительно будет равна 400 минутам? Ответ дайте в рублях.
В5. Решите уравнение
.
В6. Сторона AB треугольника ABC равна 20. Противолежащий ей угол C равен 150°.
Найдите радиус окружности, описанной около этого треугольника.
В7. Найдите
, если
.
В8.
В9. В правильной четырехугольной пирамиде
вершина,
,
. Найдите длину отрезка
точка
.
— центр основания,
В10. На семинар приехали 5 ученых из Австрии, 4 из Германии и 6 из Сербии. Порядок
докладов определяется жеребьёвкой. Найдите вероятность того, что десятым окажется
доклад ученого из Сербии.
В11. Объем первого цилиндра равен 90 м3. У второго цилиндра высота в 2 раза больше, а
радиус основания — в 3 раза меньше, чем у первого. Найдите объем второго цилиндра.
Ответ дайте в кубических метрах.
В12. Высота над землeй подброшенного вверх мяча меняется по закону
, где h — высота в метрах, t — время в секундах, прошедшее с
момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров?
В13. Два мотоциклиста стартуют одновременно в одном направлении из двух
диаметрально противоположных точек круговой трассы, длина которой равна 40 км.
Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из
них на 25 км/ч больше скорости другого?
В14. Найдите наибольшее значение функции
на отрезке
.
Часть 2
Задания второй части выполняются с подробным решением и записью ответа.
С1. а) Решите уравнение sin 2x  cos 4x ; б) Найдите корни принадлежащие отрезку


  ; 2  .
С2. Дан куб ABCDA1B1C1D1 . Длина ребра куба равна 1. Найдите расстояние от вершины
A1 до плоскости AB1D1 .
x
x
x

3  16  2  81  5  36
С3. Решите неравенство 
.
2
log
3
x

x

2


1

x


С4. Расстояние между параллельными прямыми равно 4. На одной из них лежит точка C ,
а на другой – точки A и B , причем треугольник ABC –равнобедренный и его боковая
сторона равна 5. Найдите радиус окружности, вписанной в треугольник ABC.


С5. Найдите все значения a , при которых функция f  x   x 2  4 x  a 2  6 x имеет хотя бы
одну точку максимума.
С6. Найдите все тройки натуральных чисел k, m и n , удовлетворяющие уравнению 2⋅ k !=
m! − 2⋅n! (1!=1; 2!=1⋅2 = 2; n!=1⋅2⋅...⋅n) .
Критерии оценивания заданий части 2.
Критерии оценивания выполнения задания С1
Обоснованно получены верные ответы в обоих пунктах
Обоснованно получен верный ответ в пункте а или в пункте б
Решение не соответствует ни одному из критериев, перечисленных выше
Критерии оценивания выполнения задания С2
Обоснованно получен верный ответ
Решение содержит переход к планиметрической задаче, но:
- получен неверный ответ или решение не закончено;
- при правильном ответе решение недостаточно обосновано
Решение не соответствует ни одному из критериев, перечисленных выше
Критерии оценивания выполнения задания С3
Обоснованно получен верный ответ
Обоснованно получены верные ответы в обоих неравенствах системы
Обоснованно получен верный ответ в одном из неравенств системы
Решение не соответствует ни одному из критериев, перечисленных выше
Критерии оценивания выполнения задания С4
Рассмотрены все возможные геометрические конфигурации, и получен
правильный ответ
Рассмотрена хотя бы одна возможная конфигурация, для которой
получено правильное значение искомой величины или рассмотрены все
возможные геометрические конфигурации, но получен неправильный
ответ из-за одной арифметической ошибки
Рассмотрена хотя бы одна возможная геометрическая конфигурация, в
которой получено значение искомой величины, неправильное из-за
арифметической ошибки
Решение не соответствует ни одному из критериев, перечисленных выше
Баллы
2
1
0
Критерии оценивания выполнения задания С5
Обоснованно получен верный ответ
С помощью верного рассуждения получены искомые значения, возможно
неверные, из-за одной допущенной вычислительной ошибки (описки)
С помощью верного рассуждения получен неполный или неверный ответ
(возможно неверно решено верно составленное неравенство)
Баллы
4
Задача сведена к исследованию графиков кусочно-заданной функции
(приведен правильный рисунок), но ответ неверен или решение не доведено до
ответа
Решение не соответствует ни одному из критериев, перечисленных выше
2
1
0
3
2
1
0
3
2
1
0
3
2
1
0
Критерии оценивания выполнения задания С6
Баллы
Верно и обосновано найдены все возможные тройки
4
Найдены все тройки, но решение не достаточно обоснованы или допущена
3
арифметическая ошибка
Верно и обосновано найдена хотя бы одна тройки
2
Найдена хотя бы одна тройка и выполнена проверка
1
Решение не соответствует ни одному из критериев, перечисленных выше
0