Моделирование тенденции временного ряда
реклама

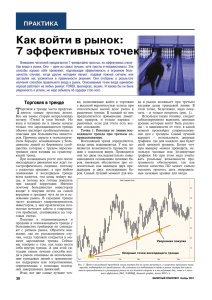
МОДЕЛИРОВАНИЕ ТЕНДЕНЦИИ РЯДА ДИНАМИКИ В таблице 1 приведены значения удельного веса площади (в процентах), удобренной минеральными удобрениями, по отношению ко всей посевной площади Волгоградской области за 1995-2006 гг. Проведем расчет параметров параболического тренда и построим графики ряда динамики и тренда. Удельный вес удобренной площади, % 5 3 5 5 2 4 8 12 16 29 32 2006 2005 2004 2003 2002 2001 2000 1999 1998 1997 1996 Год 1995 Таблица 1 – Исходные данные 27 2 Параболический тренд имеет вид: yt b0 b1 t b2 t . Определение параметров тренда и построение графиков осуществим с помощью «Мастера диаграмм»: 1) введите исходные данные в ячейки листа MS Excel; 2) на панели инструментов Стандартная щелкните по кнопке Мастер диаграмм; 3) в окне «Тип диаграммы» из списка типов выберете График и соответствующий его вид. 4) в окне «Источник данных диаграммы» закладка Диапазон данных заполните поле Диапазон (в нашем примере – Лист1!$A$1:$B$13); закладка Ряд заполните поле Подписи оси Х (в нашем примере – Лист1!$A$2:$A$13); 5) в окне «Параметры диаграммы» заполните параметры диаграммы на разных закладках; 6) в окне «Размещение диаграммы» укажите место размещения диаграммы; 7) после построения графика ряда динамики щелкните ПКМ на линии графика и в контекстном меню выберете Добавить линию тренда; 8) в диалоговом окне «Формат линии тренда» выберете вид линии тренда и задайте соответствующие параметры (рис. 1); Рис. 1 - Диалоговое окно параметров линии тренда 9) на рис. 2 представлены результаты построения графиков ряда динамики и параболического тренда. Рис. 2 – Графики исходного ВР и параболического тренда Получили уравнение параболического тренда: yt 6,318 2,167 t 0,371 t 2 . Для проверки остатков на автокорреляцию рассчитаем Критерий ДарбинаУотсона по формуле: n d ( t 2 t t 1 ) 2 . n t 1 2 t Выравненные значения ряда динамики yt определим путем подстановки фактических значений t (порядковый номер года) в уравнение тренда. Остатки εt рассчитаем по формуле: t yt yt , где εt-1 – те же значения, что и εt, но со сдвигом на один год. Результаты вычислений оформим в табл. 2. Таблица 2 – К расчету критерия Дарбина-Уотсона № 1 2 3 4 5 6 7 8 9 10 11 12 Итого yt εt εt-1 (εt- εt-1) (εt- εt-1)2 t2 4,52 3,47 3,16 3,59 4,76 6,67 9,33 12,73 16,87 21,75 27,37 33,74 147,94 0,48 -0,47 1,84 1,41 -2,76 -2,67 -1,33 -0,73 -0,87 7,25 4,63 -6,74 - 0,48 -0,47 1,84 1,41 -2,76 -2,67 -1,33 -0,73 -0,87 7,25 4,63 - -0,95 2,31 -0,43 -4,17 0,09 1,34 0,60 -0,14 8,12 -2,62 -11,37 - 0,895 5,345 0,185 17,406 0,007 1,806 0,362 0,020 65,902 6,885 129,186 228,0 0,228 0,219 3,400 1,999 7,607 7,140 1,764 0,527 0,750 52,592 21,418 45,401 143,045 Фактическое значение d=1,6 сравниваем с табличными значениями при 5%-ном уровне значимости. При n=12 лет и k=1 (число факторов) нижнее значение dL равно 0,97, а верхнее dU – 1,33. С вероятностью 0,95 принимается гипотеза Н0 и можно считать, что автокорреляция в остатках отсутствует. Следовательно, уравнение регрессии может быть использовано для прогноза. Прогнозное значение удельного веса площади, удобренной минеральными удобрениями на 2007 г. составит: y 6,318 2,167 13 0,371 132 40,85 %.