66-72

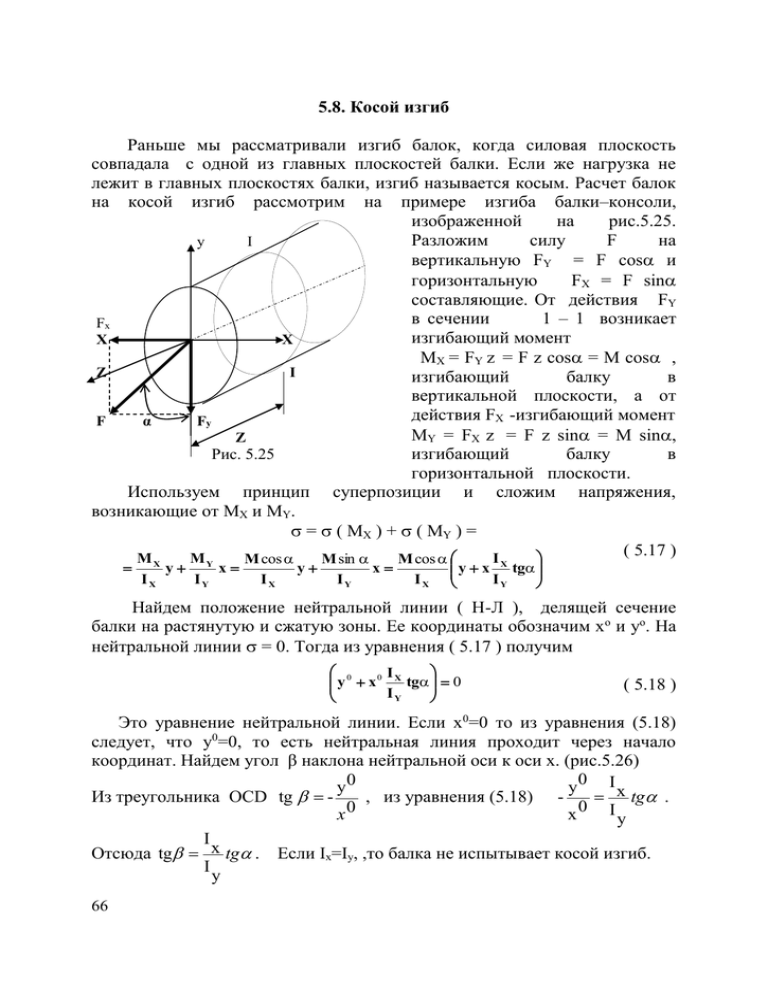
5.8. Косой изгиб
Раньше мы рассматривали изгиб балок, когда силовая плоскость
совпадала с одной из главных плоскостей балки. Если же нагрузка не
лежит в главных плоскостях балки, изгиб называется косым. Расчет балок
на косой изгиб рассмотрим на примере изгиба балки–консоли,
изображенной
на
рис.5.25.
Разложим
силу
F
на
y
I
вертикальную FY = F cos и
горизонтальную
FX = F sin
составляющие. От действия FY
в сечении
1 – 1 возникает
Fx
O
изгибающий момент
X
X
MX = FY z = F z cos = M cos ,
Z
I
изгибающий
балку
в
вертикальной плоскости, а от
действия FX -изгибающий момент
F
α
Fy
MY = FX z = F z sin = M sin,
Z
Рис. 5.25
изгибающий
балку
в
горизонтальной плоскости.
Используем принцип суперпозиции и сложим напряжения,
возникающие от MX и MY.
 =  ( MX ) +  ( MY ) =
( 5.17 )

M
M
I
M cos 
M sin 
M cos  

X
IX
y
Y
IY
x
IX
y
IY
x
IX
 y  x X tg 
IY


Найдем положение нейтральной линии ( Н-Л ), делящей сечение
балки на растянутую и сжатую зоны. Ее координаты обозначим хо и уо. На
нейтральной линии  = 0. Тогда из уравнения ( 5.17 ) получим
 0

I
 y  x 0 X tg   0
IY


( 5.18 )
Это уравнение нейтральной линии. Если х0=0 то из уравнения (5.18)
следует, что у0=0, то есть нейтральная линия проходит через начало
координат. Найдем угол β наклона нейтральной оси к оси х. (рис.5.26)
y0 I x
y0
 tg .
Из треугольника OCD tg   , из уравнения (5.18) 0
0
I
x
x
y
I
Отсюда tg  x tg . Если Ix=Iy, ,то балка не испытывает косой изгиб.
I
y
66
Опасными точками в сечении являются точки А и В, наиболее
удаленные от нейтральной линии. Их находят, проводя касательные к
контуру сечения, параллельные нейтральной линии. В точке А( х А , yA )
материал испытывает растяжение, а в точке В( хB , yB ) – сжатие. Если
материал разносопротивляется растяжению и сжатию, то проверяют
условия прочности, как на растяжение, так и на сжатие. Из формулы (5.17)
σ
σ
A
B


I
M cos
( y  x x tg )    раст
A
AI
I
x
y
I
Y
H
A
M cos
( y  x x tg )   сж
B
BI
I
x
y
Прогиб
при
косом
изгибе
перпендикулярен нейтральной линии. Это
можно
получить
самостоятельно,
рассматривая изгиб балки - консоли под
действиям
сосредоточенной
силы,
приложенной на ее конце.
Oc
σA
X β
D
F
Л
α
σВ
Рис. 5.26
5.9. Внецентренное растяжение – сжатие
В том случае, когда линия
действия нагрузки параллельна оси
стержня, но не совпадает с ней,
стержень испытывает внецентренное
растяжение или сжатие. Рассмотрим
внецентренное сжатие ( рис. 5.27,а ).
Перенесем силу F в точку О к оси
стержня. При этом к силе F добавятся
два изгибающих момента Mx = FyF
и
My = FxF ( рис. 5.27,б ).
Используем принцип суперпозиции и
определим напряжение в сечении от
центрального сжатия силой F
и изгиба от моментов Mx и Mу
Рис. 5.27
67
σσ
(F)
σ
(M )
x
σ
(M )
y
-
My
Fx
F Mx
F Fy
Fx

y
x -  F y
A Ix
Iy
A Ix
Iy
(5.19)
y
x
y y
x x
F
F
F
F
F
F
 - (1 
y
x)  - (1 
y
x)
Ix
Iy
2
2
A
A
i
i
( )
x
y
( )
A
A
Найдем положение нейтральной линии (H-Л), делящей сечение
стержня на растянутую и сжатую зоны. Координаты нейтральной линии
обозначим х0 и у0. На нейтральной линии   0 . Тогда из формулы (5.19)
получим
Y
B
H
УF
ax O
σВ
XF
X
ay
Л
A
y y0 x x0
(5.20)
1 F  F  0
2
2
ix
iy
Для построения нейтральной линии
вычислим отрезки, ах- это х0 при у0 = 0 и ау
– это у0 при х0 = 0, отсекаемые нейтральной
линией на осях координат ( рис. 5.28 ).
Из уравнения (5.20) при у0=0 получим
i2
X ax
y
(5.21)
1 F
 0, a x  
.
x
i 2y
F
σА
Рис. 5.28
При х0=0 получим
i2
y ay
F
1
 0, a y   x .
(5.22)
2
y
ix
F
Опасными точками в сечении являются точки А и В, наиболее
удаленные от нейтральной линии. Их находят ,проводя касательные к
контуру сечения, параллельные нейтральной линии. В точке А ( х А, уА )
материал испытывает растяжение, а в точке В ( хB, уB ) сжатие. Если
материал разносопротивляется растяжению и сжатию, то проверяют
условия прочности как на растяжение, так и на сжатие. Из формулы (5.19)
σ
A

x x
y y
F
(1  F A  F A )    раст
A
i2
i2
x
y
;
σ
A

x x
y y
F
(1  F B  F B )   сж
A
i2
i2
x
y
.
Для некоторых материалов нежелательно, чтоб в сечении возникали
напряжения разных знаков. Так, например, серый чугун, бетон плохо
сопротивляются растяжению. Для стержней из таких материалов находят
68
ядро сечения - область, расположенную вокруг центра тяжести сечения и
обладающую следующим свойством: если внецентренную нагрузку
приложить внутри ядра сечения, то напряжения в сечении будут одного
знака. Построим ядро сечения для прямоугольного ( рис. 5.29,а ) и
круглого ( рис. 5.29,б ) сечений.
H
Л
y
H
y
b/4
О
III
b/4
II
IV
O
x
h
Л
d
4
x
I
I
b
d
б
a
Рис. 5.29
Так как нейтральная линия не должна пересекать сечение, то есть
делить его на растянутую и сжатую зоны , то предельное ее состояние –
касательная к контуру сечения. Для прямоугольного поперечного сечения
( рис. 5.29,а ), отрезки, отсекаемые нейтральной линией Н-Л на осях
координат, равны
аx  ,
h
ay  .
2
Тогда из выражений ( 5.21 ) и ( 5.22 ) получим
i 2y
x 
 0,
F
ax
I
i 2x
bh 3
h
x
y 

 .
F
ay
h
Aa
6
y 12bh( )
2
Отложим точку I с такими координатами. Проведем нейтральные линии
через другие стороны прямоугольного контура и найдем координаты точек
II, Ш и IV. Соединим их и получим контур ядра сечения.
Для круглого поперечного сечения ( рис. 5.29, б ), отрезки,
отсекаемые нейтральной линией
Н-Л
на осях координат,
равны
аx  ,
ay 
d
.
2
Тогда из выражений ( 5.21 ) и ( 5.22) получим
i 2y
x 
 0,
F
ax
I
i2
nd 4
d
y  x  x  .
F
ay
Aa
8
nd 2 d
y
64
( )
4 2
Отложим точку I с такими координатами. Поворачиваем нейтральную
линию как касательную к контуру и получим ядро сечения в виде круга.
69
5.10. Изгиб с кручением
Если в поперечном сечении стержня равна нулю только продольная
сила N , то стержень испытывает изгиб с кручением. Таким образом, задача сводится к расчету стержня на косой изгиб и кручение. Наиболее часто
изгиб с кручением испытывают валы круглого или кольцевого сечений. В
этом случае IX = IY и мы имеем не косой, а плоский изгиб для каждого
сечения в своей плоскости. В этом случае расчет вала на изгиб с кручением проводится следующим образом:
- находим значения крутящих моментов и строем эпюру MК;
- определяем нагрузки, изгибающие вал в горизонтальной и вертикальной плоскостях и строем эпюры изгибающих моментов MX и MY ;
- находим суммарные изгибающие моменты в сечениях вала по формуле
M изг  M x2  M y2 ;
- находим опасные сечения вала, в которых величины крутящего и
суммарного изгибающих моментов являются либо максимальными,
либо достаточно большими;
- наиболее напряженными точками в опасных сечениях вала являются
точки на его периферии, в которых касательные и нормальные
M
M
 MAX  X .;
 MAX  K ,
напряжения максимальны :
WP
WX
- так как материал вала испытывает плоское напряженное состояние, расчет проводим с использованием критерия прочности и пластичности.
Валы обычно изготавливаются из малоуглеродистой стали, поэтому
используем критерий наибольших касательных напряжений или
энергетический критерий. Для этого по формуле ( 3.8 ) определяем
величины главных напряжений и подставляем их в уравнения ( 3.10 ) и
( 3.11 ). Учитывая, что WP = 2 WX , условие прочности запишем для
проверочного расчета
M расч. max
Wx
   ,
2
2
где M расч.max  M изг  М к . - расчетный момент по критерию наибольших
2
2
касательных напряжений, или M расч.max  M изг  0.75М к . -расчетный
момент по энергетическому критерию;
- при проектировочном расчете размеры поперечного сечения
найдем из условия
WX 
70
M расч. max
[ ]
.
вала
5.11. Расчет винтовых цилиндрических пружин
Геометрия пружины определяется средним диаметром витка D ,
числом витков - n; углом подъема витка - . Шаг пружины
S  D  tg . Обычно S<<D и <5. Пружины растяжения, сжатия и
кручения отличаются отделкой концов ( рис. 5.31 ).
Рассмотрим пружины из круглой проволоки диаметром d.
F
F
F
m
m
n
I
про
F
F
F
а
б
Рис. 5.31
Ось
в ол
ок и
в
Рис. 5.32
Расчет пружин растяжения – сжатия. Используем метод
сечений ( рис. 5.32 ). В поперечном сечении проволоки, параллельно оси
пружины действуют силы F и
D
m
m

F
+
. В нормальном поперечном
+
2
Mk
сечении проволоки ( рис. 5.33 )
возникают внутренние силы:
+
Горизонталь
N
D
MИЗГ
M

m

cos


F
cos  ,
k
n
2
ds
D
M изг  m  sin   F sin  ,
2
Q F
Q  F cos  и N  F sin  .
Рис. 5.33
Рассчитаем пружину на прочность.
Влиянием Мизг и N пренебрегаем так. как  мал ( sin0; cos1 ).
В поперечном сечении возникают касательные напряжения от поперечной
силы Q и от крутящего момента Мк.
 Q  
   Q     M  
k
Q F4

F d 2
;
 ( Mx) 
M x FD  16 8FD


.
Wp
2d 3
d 3
D
4 F 8FD 4 F
c





1

2
c
, где
d - индекс пружины.
d 2 d 3 d 2
71
8FD
D
 max 
  .
 1 ,
то получим
d 3
d
Для пружинной стали:   (200  800)МПа .
Определим перемещение пружины. Пренебрегаем перемещениями
от действия Q, а также от действия N и Мизг , которые малы, так как sin
мал.
Остается перемещение от Мкр. Используем интеграл Мора для
определения вертикального перемещения  пружины. Приложим
фиктивную единичную силу   1 в направлении перемещения.
D2F
FD 2
M k Mk dz
D
D
dz 
l ,
Тогда M k  cos   .   
. Откуда  
4
GI
4
GI
GI
2
2
k
k
k
l
l
Так как

l  Dn ,
d 4
Ik  Ip 
и
32
где l - - длина развернутой пружины,
FD 2n

4GI k ;
8FD 3n

Gd 4
Отогнутая часть для пружин растяжения и по ¾ витка с каждой
стороны для пружины сжатия в расчет не принимаются.
Расчет пружин кручения. В вертикальном сечении проволоки проходящем через ось пружины, действует горизонтальный момент m (рис5.34).
+
+
Mk
m
+
m
Рис. 5.34
Mизг
n
Рис. 5.35
В нормальном сечении проволоки возникают MK = m sin и Mизг = m cos
m
  .
(рис.5.35). Пренебрегаем MK.Условие прочности запишется  max 
Wx
Определим перемещение пружины. Для определения угла
закручивания всей пружины используем интеграл Мора. Приложим к
пружине единичный момент M изг  1 . Тогда перемещение пружины

l
М изг  Мизг  dz
m  1  dz ml mDn mDn  64 64mDn





.
4
EI
E

d
Ed 4
EI x
EI
EI
x
x
x
l
Величина усилия F, или момента m, при которой деформация
пружины равна 1 , называется жесткостью пружины – С. Для пружин
растяжения – сжатия
72
Gd 4
С
, для пружин кручения
8D3n
Ed 4
C
.
64Dn