МАГНИТНОЕ ПОЛЕ Основные понятия и формулы

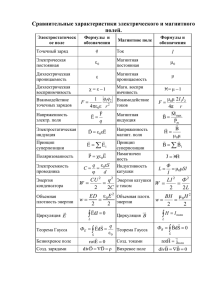
МАГНИТНОЕ ПОЛЕ
Основные понятия и формулы
Закон Био-Савара-Лапласа:

 0  dl , r I
 0 I sin
dB 
или dB 
dl ,
3
2
4

r
4

r

где dB - магнитная индукция поля, создаваемого элементом
проводника с током I;

r - радиус-вектор, проведенный от элемента проводника к
точке, в которой определяется магнитная индукция;
 - угол между радиус-вектором и направлением тока в
элементе
 проводника;
dl - вектор, равный по модулю длине dl проводника и
совпадающий по направлению с током (элемент
проводника).
Магнитная индукция в центре кругового витка с током
определяется по формуле:
 0l
, где R - радиус витка.
B
2R
Магнитная индукция на оси кругового тока
0
 0  2R 2 I
2R 2 I
B

;
4 R 2  h 2 3
4 R 2  h 2 3 2


где h - расстояние от центра витка до точки, в которой определяется
магнитная индукция.
Магнитная индукция поля, созданная прямым бесконечно длинным
проводником с током
 I
B 0 ,
2r0
где r0 - кратчайшее расстояние от оси проводника до точки, в
которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком проводника с
током (рис. 3.1), может быть найдена по формуле:
 I
B  0 cos 1  cos  2  .
4 r
На рис. направление вектора магнитной индукции


B обозначено точкой - это значит, что вектор B
направлен перпендикулярно плоскости чертежа к нам.
Сила, действующая на проводник с током в
магнитном поле (закон Ампера),

 

dF  I dl , B

или dF  IBdl sin  ,
где
 - угол между направлением тока в
проводнике
и вектором магнитной индукции B .

dl - вектор элемента тока проводника, проведенный в направлении
тока.
Магнитный момент плоского контура с током:


pm  nIS ,

где n - единичный вектор нормали к плоскости контура;
I - сила тока, протекающего по контуру;
S - площадь контура.
Механический (вращательный) момент сил, действующий на
контур с током, помещенный в однородное магнитное поле,



 
M  p m , B , или M  pm B sin ,


где  - угол между векторами pm и B .
Потенциальная энергия (механическая) контура с током в
магнитном поле 

П мех   pm B , или П мех   pm B cos  .
Отношение величины магнитного момента pm к величине
механического L (момента импульса) заряженной частицы, движущейся
по круговой орбите,
pm
q
,

L
2m
где q - заряд частицы; m - масса частицы.
Сила
Лоренца

 
F  q , B , или F  qB sin  ,


где  - угол между векторами  и B .
Если частица движется одновременно в электрическом и
магнитном полях, то сила действующая на частицу определяется по
формуле
 Лоренца:

 
F  qE  q , B .


Магнитная индукции
и
напряженность
магнитного поля
B
H


связаны соотношением B   0 H ,
 
 
где  - магнитная проницаемость среды; в вакууме   1,
Гн
- магнитная постоянная.
 0  4   10 7
м
Магнитная индукция внутри соленоида и тороида:
B  0 nl.
где n - отношение числа витков соленоида к его длине.