Задачи с решениями - Физический факультет КемГУ

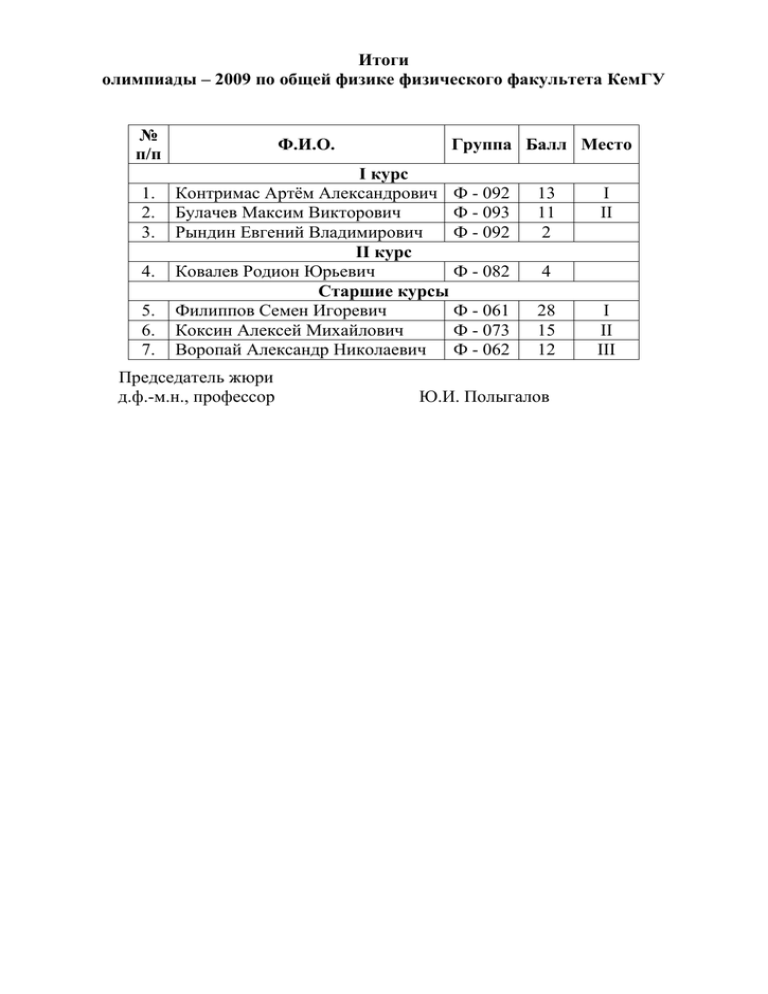
Итоги
олимпиады – 2009 по общей физике физического факультета КемГУ
№
п/п
1.
2.
3.
4.
5.
6.
7.
Ф.И.О.
Группа Балл Место
I курс
Контримас Артём Александрович Ф - 092
Булачев Максим Викторович
Ф - 093
Рындин Евгений Владимирович
Ф - 092
II курс
Ковалев Родион Юрьевич
Ф - 082
Старшие курсы
Филиппов Семен Игоревич
Ф - 061
Коксин Алексей Михайлович
Ф - 073
Воропай Александр Николаевич
Ф - 062
Председатель жюри
д.ф.-м.н., профессор
13
11
2
I
II
4
28
15
12
Ю.И. Полыгалов
I
II
III
1 курс
1. Кот Леопольд бежал по прямой дороге из пункта А. Вначале он в течение
промежутка времени τ = 1 с бежал с ускорением а = 1 м/с2 (без начальной
скорости). После этого он начал тормозить так , что его ускорение стало
равным по величине 2а и спустя некоторое время он вернулся назад в пункт А.
Чему равна средняя путевая скорость кота Леопольда?
Возможное решение
a 2
За время τ кот Леопольд пробежал расстояние S1 
, затем до
2
2
2atост
остановки он пробежал расстояние S2  (a )tост 
, где tост - время от
2
начала торможения до остановки. Время tост определяем из
уравнения: a  2atост  0;
tост 

2
. Пройденный котом Леопольдом путь S
= S1 + S2 = 3aτ2/4. Время возврата определяется из
3a 2 2at32

уравнения:
4
2
 t3 
3
 . Время пройденного котом
2
Леопольдом всего пути, следовательно, равно:

3
t   
.
2 2
V 
Средняя путевая скорость П
3a
м
 0, 63 .
1
с
2[1  (1  3)]
2
2. На гладкой горизонтальной поверхности льда покоится доска массы М и
длины L, на одном из концов которой сидит котенок массы m. С какой
наименьшей скоростью относительно льда он должен прыгнуть, чтобы попасть
на другой конец доски? Какой угол α0 с горизонтом должна составлять эта
скорость, чтобы котенок затратил на прыжок к другому концу доски минимум
энергии?
Возможное решение
Пусть котенок прыгнет со скоростью V0 под углом α к горизонту, а u –
скорость доски сразу после прыжка котенка. Время полета котенка
t
2V0 sin 
.
g
Котенок попадет на другой конец доски, если ut  V0 cos   t  L . Учитывая, что по
закону сохранения импульса, mV0 cos   Mu , получим
V0 
Lg
.
(1  m / M ) sin 2
Отсюда, наименьшая скорость
V0 
Lg
1 m / M
Котенок совершил работу, которая пошла на увеличение кинетической энергии
доски и самого котенка
Mu 2 mV02
mM Lg
1
m




 (1  cos 2  ) .
2
2
m  M 2 sin 2
M
m
Эта энергия минимальна при tg 0  1  .
M
W
3. В калориметр с горячим чаем бросили кубик льда, имеющий температуру
00С. К моменту установления теплового равновесия температура чая
понизилась на Δt1 = 12 0С. Когда в калориметр бросили другой такой же кубик
льда, температура чая понизилась еще на Δt1 = 10 0С. Найдите массу кубика
льда. Первоначальная масса чая М = 100 г. Теплоемкостью калориметра,
теплообменом с окружающей средой и примесями заварки в чае пренебречь.
Возможное решение
Запишем уравнение теплового баланса для первого случая:
cM t1  m  cm(t1  t1 ) , где m – масса кубика льда, λ –
удельная теплота плавления льда, с – удельная теплоемкость воды, t1 –
исходная температура чая. Отсюда

M

  1 t1   t1
c
m

(1)
В случае бросания в чай второго кубика мы можем записать уравнение,
аналогичное уравнению (1):

M

 1 (t1  t2 )   t1 .

c
 2m 
(2)
Исключая из (1) и (2) правые части, получим:
M

M

 1 (t1  t2 ) ,
  1 t1  
m

 2m 
откуда легко найти отношение масс:
2 t 2
M

 10 , следовательно, m =10 г.
m t1  t2
4. Два свинцовых шарика, отпущенные с большой высоты, достигают при
падении в воздухе установившихся скоростей v1 = 100 м/c и v2 = 150 м/c. Чему
равна установившаяся скорость падения, если шарики соединить длинной
невесомой нитью? Сила сопротивления пропорциональна площади
поперечного сечения и квадрату скорости.
Решение
4
m1 g  kS1v12  k R12v12   R13  g ,
3
4
m2 g  kS2v22  k R22v22   R23  g .
Без нити:
3
3 k 2
3 k 2
R1 
v1 ,
R1 
v1 .
(1)
4 g
4 g
4
3
4
3
С нитью:
4 3
v 2 ( R12  R22 ) 
( R1  R23 ).
3k
  R13 g    R23 g  k R12v 2  k R22v 2 ,
(2)
1
2
v v 
С учетом (1) и (2): v  
  143 м / с.
v

v


5. Два одинаковых плоских конденсатора емкости С соединены параллельно и
заряжены до напряжения U. Пластины одного из конденсаторов разводят на
большое расстояние. Найти напряжение на втором конденсаторе и его энергию.
6
1
4
1
6
2
4
2
Решение
До раздвигания пластин одного из конденсаторов их заряды равны:
q = CU
После раздвигания пластин одного из конденсаторов его емкость будет равна
нулю и по закону сохранения заряда заряд второго конденсатора станет равным
2q (заряд стекается на пластины второго конденсатора). Тогда напряжение на
этом конденсаторе станет равным:
U 
2q 2CU

 2U .
C
C
Энергия этого конденсатора будет равна:
1 4q 2
W
 2CU 2
2 C
2 курс
1. На гладкой горизонтальной поверхности массивной плиты покоится клин
массой М и углом наклона α . Клин плотно прилегает к поверхности плиты.
Шар массой m летит горизонтально и ударяется о гладкую наклонную
плоскость клина (удар упругий). В результате клин начинает двигаться по
плите. Найдите отношение
m
, если через некоторое время шар попадает в ту
M
же точку на клине, от которой он отскочил.
Решение
По закону сохранения импульса:
mv0 = (m + M)vx , (1)
где vx – горизонтальная составляющая скорости шара после столкновения,
равная скорости клина (в противном случае шар не упадет в ту же точку на
клине).
y
F
m
M

x
По закону сохранения энергии:
mv02 (m  M ) 2 m 2

vx  v y (2)
2
2
2
По второму закону Ньютона:
mv y  F t cos 
(3)
Mvx  F t sin 
(4)
Из (1) – (4) следует:
m cos(2 )

M
sin 2 
2. Палочка длиной l на горизонтальной опоре около стенки. На нижнем конце
палочки сидит жук. В некоторый момент времени палочка начинает двигаться
так, что ее нижний конец движется с постоянной скоростью v по
горизонтальной опоре, а верхний скользит вдоль стенки. В этот же момент жук
начинает двигаться вдоль палочки с постоянной (относительно палочки)
скоростью v1 . На какую максимальную высоту над горизонтальной опорой
поднимется жук?
Решение
Ясно, что высота, на которой жук находится, имеет максимум.
Действительно, в начальный момент времени жук находится на поверхности, в
момент падения палочки на поверхность – тоже. Пусть движение жука
началось в момент t = 0. Из рисунка видно, что в момент времени t жук
находится над горизонтальной поверхностью на высоте
h(t )  v1t sin 
(1)
С другой стороны
cos  
vt
l .
(2)
Отсюда:
h(t )  v1t 1  (vt / l ) 2 .
(3)
Продифференцируем эту функцию и приравняем нулю.
В результате найдем момент времени tm, отвечающий максимальной высоте.
Ответ: tm 
2 l
1
; hm  l .
2 m
2
3. Волчок, масса которого m = 1,0 кг и момент инерции относительно
собственной оси I = 4,0 (г·м2) вращается с угловой скоростью
ω = 310 (рад/с). Его точка опоры находится на подставке, которую перемещают
в горизонтальном направлении с постоянным ускорением a = 1 (м/с2).
Расстояние между точкой опоры и центром масс волчка l = 10 см. Найдите
модуль и направление вектора
 - угловой скорости прецессии волчка.
Решение
Угловая скорость
 прецессии волчка удовлетворяет уравнению
[ , L]  M ,
(1)
L
где
- момент импульса волчка, M - момент внешних сил и сил инерции.
M  m[l , g  a ] .
L  I ;
Подставим (2) в (1):
[ , I  ]  m[
l

, g  a]
(2)
(3)
Из (3) видно, что   параллельно g  a . Следовательно:
ga
ml g 2  a 2
      ml

.
I
I
Так как g  a , то
 составляет с g угол  , который определится из
a
tg


соотношения
g.
0
Ответ:   0,8 рад / c,   6 .
4. Определите КПД (η) эллиптического
цикла, изображенного на рисунке.
T
T1
T2
S1
S
S2
Решение
По определению:
  1
Q()
Q(  )
,
где Q(-) – тепло, отданное рабочим телом цикла; Q(+) – тепло, поступившее к
рабочему телу. Учитывая, что площадь эллипса равна πаb, из рисунка найдем:
T1  T2

( S 2  S1 )  (T1  T2 )( S 2  S1 )
2
4
T T

Q (  )  1 2 ( S 2  S1 )  (T1  T2 )( S 2  S1 )
2
4
T1  T2 
 (T1  T2 )
2
4
  1
T1  T2 
 (T1  T2 )
2
4
5. Смесь воды и ее насыщенного пара занимает некоторый объем при
температуре 900 С. При этом масса воды составляет 29 % от массы всей смеси.
Объем воды очень мал по сравнению с объемом смеси. Если смесь нагревать
медленно и изохорически, вся вода испарится к тому моменту, когда
температура достигнет 1000 С. Чему равно значение давления насыщенного
пара при 900 С.
Q() 
Решение
Пусть m –масса смеси воды и ее насыщенного пара. Тогда согласно уравнению
Клапейрона-Менделеева:
PV 
0, 71m
RT1 ,
MП
(1)
где Т1 = 363 К. Сразу после испарения воды при температуре кипения воды
Т2 = 373 К давление должно быть атмосферным ( P0 = 105 Па). Следовательно,
PV

0
0, 71m
RT2 .
MП
(2)
Из (1) и (2) следует:
P 363

 P  P0  0,97.
P0 373
3 – 5 курсы, магистры (вариант 1)
1. На рисунке изображена стеклянная призма, поставленная
на монету М. Можно ли увидеть монету через боковую грань
призмы?

M
Решение
На рисунке показан один из лучей, идущих от монеты.
Так как
sin  
sin 
, а sin   cos  , то
n
sin 2 
sin   1 
,
2
n
где n – показатель преломления стекла. Но изображенный
на рисунке луч сможет выйти через боковую грань
призмы лишь при условии
sin   1/ n .
В противном случае произойдет полное внутреннее отражение. Следовательно
должно выполняться неравенство
sin 2  1
1
 .
n2
n
Откуда
sin 2   n2  1  n 2  2  n  2  1, 41.
А так как показатель преломления стекла больше этого значения, то увидеть
монету через боковую грань призмы невозможно.
m2 = 0,4 кг
m1 = 0,2 кг
О
•
2. Два бруска, массы которых 200 и 400 г,
соединены пружиной жесткостью 0,5 Н/м.
Пружина сжата при помощи нити, проходящей внутри пружины. Нить
пережигают. Определить период колебаний брусков.
Возможное решение
Если пережечь нить, то бруски начнут удаляться друг от друга, потом
сближаться, но центр масс системы (по закону сохранения импульса) все время
остается неподвижным. В этой точке можно мысленно закрепить пружину и
решать задачу о движении каждого бруска в отдельности. Тяжелый груз при
этом колеблется на короткой части пружины, легкий – на длинной. Найдем
положение центра масс системы. Если расстояния от него обозначить
х1 и х2, то система уравнений для их нахождения имеет вид:
 x1  x2  l


 m1 x1  m2 x2
x1  l
m2
2
 l
m1  m2 3
x2  l
m1
1
 l
m1  m2 3
Таким образом, тяжелый брусок колеблется на более короткой пружине, чем
легкий. Коэффициент жесткости пружины обратно пропорционален ее длине.
Это означает, что
k2 = 3k = 1,5 H/м, k1 = 1,5k = 0,75 H/м. Теперь можно определить период
колебаний брусков
T  T1  T2  2
m1
m2
0, 2
 2
 2
 3, 24 c .
k1
k2
0.75
3. В электрической цепи, показанной на рисунке, ЭДС источника тока равна
12 В, емкость конденсатора 2 мФ,
индуктивность катушки 5 мГн,
R

сопротивление лампы 5 Ом и
C
L сопротивление резистора 3 Ом. В
К
начальный момент времени ключ К замкнут.
Какая энергия выделится в лампе после
размыкания ключа? Внутренним сопротивлением источника тока, а также
сопротивлением катушки и проводов пренебречь.
Решение
Пока ключ замкнут, через катушку L течет ток I, определяемый
сопротивлением резистора: I 

R
, конденсатор заряжен до напряжения U = ε .
LI 2
Энергия электромагнитного поля в катушке L:
.
2
C 2
Энергия электромагнитного поля в конденсаторе
2
.
После размыкания ключа начинаются электромагнитные колебания, и вся
энергия, запасенная в конденсаторе и катушке, выделяется в лампе и на
резисторе:
C 2 LI 2 C 2  2
E


 2 L  0,184 Дж.
2
2
2
2R
Согласно закону Джоуля-Ленца, выделяемая на резисторе мощность
пропорциональна его сопротивлению. Следовательно, энергия 0,184 Дж
выделяется в лампе и на резисторе пропорционально их сопротивлениям, и на
5
лампу приходится EЛ  Е  0,115 Дж.
8
4. Тонкий проводящий диск толщиной d и площадью S падает в вертикальном
положении в горизонтальном магнитном поле
В индукцией B, линии которого параллельны
плоскости проводника. Найдите ускорение, с
которым падает диск, если его масса m .
Решение
g
Под действием силы Лоренца происходит разделение
зарядов и падающий в магнитном поле проводящий диск становится
заряженным конденсатором. Напряженность электрического поля между
пластинами этого конденсатора найдется из соотношения: qvB = qE.
Тогда заряд q  CU 
Сила тока I 
0S
d
Ed   0 SE   0 SvB .
dq
  0 SaB  Сила Ампера
dt
По второму закону Ньютона:
a
mg
m   0 SB 2 d
FA  IBd   0 SaB 2 d .
ma = mg – FA . Отсюда
.
5. Один моль гелия расширяется так, что его давление линейно зависит от
объёма. Температуры в исходном и конечном состояниях одинаковы.
Вычислите работу, совершаемую газом, если известно, что в ходе
рассматриваемого процесса разность между максимальной и минимальной
температурой равна ΔT, а объём гелия увеличивается в k раз, причём k > 1.
Решение
Пусть в начальном состоянии объем гелия V0, давление p0, а
температура T0. По условию конечный объем V1. Так как
начальная и конечная температуры газа равны, из уравнения
состояния найдём конечное давление: p1 = p0/k.
Работа, совершённая газом в указанном процессе, численно равна площади
под графиком :
p 
pV
1
A   p0  0  (kV0  V0 )  0 0 (k 2  1).
2
k 
2k
(1)
Запишем уравнение процесса расширения гелия:
p0  p p0  p1 1 p0


.
V  V0 kV0  V0 k V0
Перепишем его в виде:
p V
p0 k  1

p0 .
kV0
k
(2)
Продифференцируем это уравнение по объёму:
p
dp
 0  0.
dV kV0
(3)
Найдём объём и давление гелия в состоянии, где его температура
максимальна. Для этого продифференцируем уравнение состояния (pΥ = νRT)
по объёму:
V
Из (2), (3) и (4) найдём:
Vmax  V0
dp
dT
 p  R
.
dV
dV
k 1
,
2
(4)
pmax  p0
k 1
.
2k
Запишем уравнения Менделеева-Клапейрона для начального состояния и
состояния, в котором температура гелия максимальна и равна T0 + ΔT:
p V  k 1 
 0 0
   R(T  T ).
k  2 
2
p0V0   RT0 ,
pmaxVmax
Из этих двух уравнений найдём
 1  k  1 2  p0V0
 RT  p0V0  
 1 
(k  1) 2 .
 k  2 
 4k


С учётом последнего уравнения, выражение для работы примет вид:
 k 1 
A  2 RT 
.
 k 1 
Два бруска, массы которых 200 и 400 г,
соединены пружиной жесткостью 0,5 Н/м.
m1 = 0,2 кг
О
Пружина сжата при помощи нити,
•
проходящей внутри пружины. Нить
пережигают. Определить период колебаний брусков.
m2 = 0,4 кг
Возможное решение
Если пережечь нить, то бруски начнут удаляться друг от друга, потом
сближаться, но центр масс системы (по закону сохранения импульса) все время
остается неподвижным. В этой точке можно мысленно закрепить пружину и
решать задачу о движении каждого бруска в отдельности. Тяжелый груз при
этом колеблется на короткой части пружины, легкий – на длинной. Найдем
положение центра масс системы. Если расстояния от него обозначить
х1 и х2, то система уравнений для их нахождения имеет вид:
 x1  x2  l


 m1 x1  m2 x2
x1  l
m2
2
 l
m1  m2 3
x2  l
m1
1
 l
m1  m2 3
Таким образом, тяжелый брусок колеблется на более короткой пружине, чем
легкий. Коэффициент жесткости пружины обратно пропорционален ее длине.
Это означает, что
k2 = 3k = 1,5 H/м, k1 = 1,5k = 0,75 H/м. Теперь можно определить период
колебаний брусков
T  T1  T2  2
m1
m2
0, 2
 2
 2
 3, 24 c
k1
k2
0.75
3 – 5 курсы. Магистры (вариант 2)
1. К неподвижному бруску, расположенному на гладкой горизонтальной поверхности,
прикреплены две невесомые пружины с жесткостями К1 и К2. Второй конец пружины с
жесткостью К1 прикреплен к вертикальной стене. Свободный конец пружины с жесткостью
К2 начинают горизонтально перемещать с постоянной скоростью V0. Через некоторое время t
= τ, ускорение бруска оказалось равным нулю. Чему равны удлинения пружин в этот
момент?
Решение
Пусть за время  первая пружина
K1
K2 v
растянулась на Х1, а вторая на Х2. Так как в
o
момент t= ускорение бруска равно нулю, то имеет
место равновесие упругих сил:
K1  X 1  K 2  X 2
(1)
X  X 1  X 2  V0  
(2)
Суммарное растяжение пружин
Из (1) и (2) следует ответ:
X 1 
2.
K 2  V0  
;
K1  K 2
X 2 
K1  V0  
.
K1  K 2
2. Перемычка MN скользит по двум вертикальным направляющим под действием силы
тяжести и силы упругости, вызванной растяжением
C
(сжатием) пружинки жесткостью k. Пружинка
вертикальна, концы пружинки изолированы от
электрического тока. Нижний конец пружинки
прикреплен к середине перемычки. Длина перемычки
 B k
L, масса m, Вверху цепь замкнута на конденсатор
емкостью С. Вся система находится в однородном
магнитном поле с индукцией В. Каков будет период
M
N
колебаний перемычки. Сопротивлением проводников и
силами трения пренебречь.
x
Возможное решение
По второму закону Ньютона:
ma  mg  kx  IBL ,
(1)
где I – индукционный ток. Находим его с помощью закона Фарадея:
q
dq
  BVL 
 q  CBVL  I 
 CBLa . Тогда уравнение (1) приводится к
C
dt
дифференциальному уравнению гармонического осциллятора:
..
x  02 x 
mg
,
m  B 2 L2C
где
02 
T
k
. Следовательно, период колебаний
m  B 2 L2C
2
0
 2
m  B 2 L2C
k
.
4. Имеется пластиковый сосуд в форме прямоугольного параллелепипеда АВСDHKLM с
тонкими стенками. Вертикальные грани сосуда AHKB
K
L
и DMLC металлизированы. Сосуд заполняют жидким
диэлектриком плотности ρ и диэлектрической
M
H
проницаемостью ε0 , а затем его подключают к батарее
с ЭДС Е. Диэлектрик и пластины химически не
A
взаимодействуют. В нижней грани сосуда открывают
B
отверстие, через которое за время t0 = 1 c откачивают μ
C
килограммов диэлектрика. Определить зависимость
показаний амперметра от времени. Батарея и
D
A
амперметр - идеальные. AD = d.
Возможное решение
Пусть a,b,d –линейные размеры сосуда. Сосуд с
налитым диэлектриком можно рассматривать как два параллельно соединенных
конденсатора (см. рис.). Тогда
H
M
 (a  Vt )b  0Vtb
C  C1  C2  0

;
d
d
заряд эквивалентного конденсатора q = EC;
Vt
dq
dC
a
E
Ток через амперметр I 
;
dt
dt
ε

  Vbd  t0  V 
;
D
C
bd   t0
2
A
.
 0 (1   ) 
IE
d 2  t0
E
5. На дифракционную решетку с периодом d = 0,01 мм нормально к поверхности решетки
падает параллельный пучок монохроматического света с длиной волны λ = 600 нм. За
решеткой параллельно ее плоскости расположена тонкая собирающая линза с фокусным
расстоянием f = 5 см.
Чему равно расстояние между максимумами первого и второго порядков на экране,
расположенном в фокальной плоскости линзы?
Решение
На экране наблюдаются светлые и темные полосы в результате интерференции световых
пучков, образующихся в результате дифракции света на решетке. Прозрачную щель решетки
можно представить согласно принципу Гюйгенса-Френеля совокупностью тонких
светящихся нитей, параллельных краям щели, которые излучают когерентные
цилиндрические волны. Поскольку в условии ничего не говорится о ширине щелей, будем
считать их достаточно узкими. Светлые полосы на экране свидетельствуют о том, что волны
от разных щелей приходят в эти точки в одинаковой фазе и интерферируют, давая максимум
интенсивности световой волны.
Приводим рисунок с ходом лучей от двух щелей через линзу с соблюдением законов
геометрической оптики, демонстрирующих путь волн, интерферирующих в заданной точке
экрана.
1
x1
A
d
φ1
C
2
φ
x0
O
F
На рис. показан ход лучей 1 и
2 (луч – направление
распространения световой
волны), образующих
интерференционный
максимум первого порядка на
расстоянии х1 от
центрального (нулевого)
максимума. Ход лучей,
образующих второй
максимум, строится
аналогично, только лучи 3 и
4 пойдут под большим по
сравнению с φ1 углом φ2 по
отношению к главной оптической оси линзы.
Вычисляем разность хода лучей s1 и s2, образующих первый и второй максимумы:
s1 = BC = d sinφ1, s2 = d sinφ2 .
Прохождение лучей через линзу не приводит к изменению их разности фаз.
Используем условие интерференционного максимума первого и второго порядков: d
sinφ1 = λ, d sinφ2 = 2λ .
Используем геометрические соотношения для вычисления расстояния между первым
и вторым максимумами с использованием фокусного расстояния линзы. Из рис. видно, что:
x1 = F tgφ1, x2 = F tgφ2 . Откуда следует, что искомое расстояние между максимумами равно:
x2 – x1 = F(tgφ2 – tgφ1) .
Доказываем малость углов φ1 и φ2 и используем их малость для замены тангенсов
углов их синусами.
Учитывая, что при малых углах φ (малость углов sinφ = 0,06 → φ ≈ 30 можно
проверить используя данные задачи) sinφ ≈ tgφ ≈ φ, получим:
x2 – x1 = F(sinφ2 – sinφ1) =F(2λ/d – λ/d) = Fλ/d .
Подставив численные значения физических величин, выраженных в СИ,
получаем ответ: x2 – x1 =3·10 –3 м = 3 мм.