по ... (дисциплина) для специальности
реклама

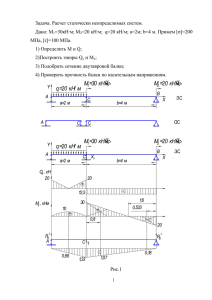
УТВЕРЖДАЮ Заведующий кафедрой ОНД В.А.Дремук подпись « 10 » мая 2011 г. протокол № 10 Методические указания для подготовки к входному компьютерному тестированию по Механика материалов (дисциплина) для специальности 1-74 06 01 «Техническое обеспечение процессов сельскохозяйственного производства» Барановичи 2011 1 ВВЕДЕНИЕ Данные методические указания содержат тематический план курса «Механика материалов» , примеры решения задач, вопросы для подготовки к компьютерному тестированию, список учебной литературы. ТЕМАТИЧЕСКИЙ ПЛАН № п/п 1. 1.1 1.2 1.3 1.4 1.5 Название раздела, темы Предмет, содержание и задачи курса. Связь с общенаучными, общеинженерными и специальными дисциплинами. Виды тел. Реальный объект и расчетная схема. Внешние силы и их классификация. Допущения, принимаемые в механике. Метод сечений для определения внутренних усилий. Продольные силы и их эпюры. Определение вращающих моментов. Крутящие моменты и их эпюры. Поперечная сила и изгибающий момент. Взаимосвязь между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки. Выводы, вытекающие из соотношения между М, Q и q. Напряжение полное, нормальное и касательное. Зависимости между внутренними силовыми факторами и напряжениями Понятие о перемещениях и деформациях. Связь перемещений и деформаций. Диаграмма растяжения малоуглеродистой стали. Пределы пропорциональности, упругости, текучести, прочности. Условный предел текучести. Характеристики пластичности. Наклеп. Диаграмма растяжения хрупких 2 материалов. Диаграммы сжатия хрупких и пластичных материалов. Влияние различных факторов на механические свойства материалов. Ползучесть. Релаксация. Длительная прочность. Допускаемые напряжения. Понятие о коэффициенте безопасности. 1.6 1.7 Особенности расчета брусьев при сложном нагружении, порядок решения задач. Косой изгиб. Внецентренное растяжение и сжатие. Изгиб с кручением. Определение диаметра вала при кручении с изгибом. Вопросы для подготовки к тестированию: Вопросы по дисциплине «Механика материалов» для специальности: 1 – 74 06 01 «Техническое обеспечение процессов сельскохозяйственного производства» 1. Содержание и задачи курса «Механика материалов». Расчеты на прочность, жесткость и устойчивость. 2. Допущения, принимаемые в курсе «Механика материалов». 3. Внешние нагрузки. 4. Метод сечений для определения внутренних усилий. 5. Продольные силы и их эпюры. 6. Поперечная сила и изгибающий момент. 7. Взаимосвязь между крутящим моментом, поперечной силой и интенсивностью распределенной нагрузки. 8. Определение вращающих моментов. Крутящие моменты и их эпюры. 9. Деформации и перемещения. 10. Напряжения: полное, нормальное, касательное. 3 11. Диаграмма растяжения малоуглеродистой стали. 12. Условный предел текучести. 13. Характеристики пластичности. 14. Наклеп. 15. Понятие о перемещениях и деформациях. Связь перемещений и деформаций. 16. Диаграмма растяжения малоуглеродистой стали. 17. Условный предел текучести. 18. Характеристики пластичности. 19. Диаграмма растяжения хрупких материалов. 20. Диаграмма сжатия хрупких материалов. 21. Диаграммы сжатия пластичных материалов. 22. Влияние различных факторов (хим. состава, закалки, скорости нагружения и температуры) на механические свойства материалов. 23. Ползучесть. 24. Релаксация. 25. Длительная прочность. 26. дифференциальное уравнение изогнутой оси балки и его интегрирование. Условия жесткости для подкрановых балок и валов. 27. Метод начальных параметров. 28. Потенциальная энергия деформации при чистом изгибе. 29. Теоремы о взаимности работ и взаимности перемещений. 30. Интеграл Максвелла-Мора для определения перемещений. 31. Способ Верещагина. 32. Статически неопределимые системы. Степень статической неопределимости, основная и эквивалентная система. Примеры решения задач ПРИМЕР 1 К ступенчатому брусу (см. рис.1) приложены силы F и kF. Исходные данные к задаче: А1 = 10 см2; А2 = 8 см2; l1 = 0,2 м; l2 = 0,5 м; l3 = 1 м; l4 = 0,3 м; k = 1,4; n = 1,2; = 0,8 мм. В задаче необходимо: 4 1) определить минимальное значение силы F, при котором исчезнет зазор между опорой и брусом; 2) заменить силу F на силу P = nF и определить: а) реакцию опоры; б) продольные силы N и построить их эпюру; в) напряжения и построить их эпюру; г) деформации каждого участка бруса, если Е 2 10 5 МПа и построить эпюру перемещений сечений; д) на сколько градусов надо охладить брус, чтобы реакция опоры исчезла, если коэффициент линейного расширения 125 10 7 град-1. При решении задачи считать, что деформации подчиняются закону Гука. Решение: Брус разбиваем на четыре участка. За участок принимают часть бруса постоянного сечения до точки приложения силы. Определим продольные силы N на каждом участке. Продольная сила в сечении численно равна алгебраической сумме всех внешних сил, действующих на рассматриваемую часть бруса. Определять значения продольных сил для данного бруса нужно со свободного конца. Если определять слева, то нужно найти значение реакции в опоре А. На участке IV справа нет сил, следовательно, N 4 0 . На участке III действует сила kF, стремящаяся растянуть брус, поэтому N положительна и равна N 3 kF . На участке II действует только сила kF, поэтому N 2 kF . На первом участке помимо силы kF действует сила F, являющаяся сжимающей для этого участка, и поэтому отрицательная N1 kF F k 1F 1,4 1F 0,4F . Определив продольные силы на каждом участке, можно найти деформацию каждого участка. Если участок удлиняется, то деформация положительна, сжимается — отрицательная. Деформацию определяют по формуле: l l1 Nl AE N1l1 0,4F 0,2 0,04F 4 10 10 F ; 4 5 6 A1 E 10 10 2 10 10 108 5 N 2 l 2 1,4 F 0,5 0,35F 35 10 10 F ; 4 11 8 A1 E 10 10 2 10 10 N l 1,4F 1 0,875F l3 3 3 87,5 10 10 F ; 4 11 8 A2 E 8 10 2 10 10 l 4 0 l 2 Для того, чтобы закрылся зазор между брусом и правой опорой необходимо, чтобы сумма деформаций всех участков равнялась зазору . l 4 35 87,510 i 10 F 0,8 10 3 126,5 1010 F 0,8 103 ; F 63,2 103 Н = 63,2 кН Выполним решение для случая 2, заменив силу F на P nF 1,2 63,2 75,8 кН. В этом случае в правой опоре возникнет реакция R. Для определения ее значения рассмотрим перемещение сечения Е. Используя закон Гука, что деформации прямо пропорциональны нагрузке, перемещение сечения Е от сил Р и kР можно определить из пропорции F P l p P n 1,2 0,8 0,96 мм F Поскольку зазор = 0,8 мм, то брус силой R будет сжат на l p величину l R l p 0,96 0,8 0,16 мм Определим деформацию бруса от силы R. В этом случае у бруса два участка. Rl1 l 2 Rl 3 l 4 R l1 l 2 l 3 l 4 A1 E A2 E E A1 A2 R 0,2 0,5 1 0,3 0,7 1,6310 3 R 1,12 10 8 R 2 1011 10 10 4 8 10 4 2 1011 l R или 6 1,12 10 8 R 0,16 10 3 ; R 1,43 10 4 Н = 14,3 кН Определим продольную силу N в каждом сечении бруса. Рассматриваем брус справа. N 4 R 14,3 кН Знак «минус» принимаем потому, что сила R сжимает участок IV. N 3 R kP 14,3 1,4 75,8 91,8 кН; N2 R kP 14,3 1,4 75,8 91,8 кН; N1 R kP P 14,3 1,4 1 75,8 16,0 кН. Строим эпюру N (см. рис. 5). Определим напряжения на каждом участке по формуле: 1 N A N1 16 10 3 16 10 6 Па = 16 МПа; A1 10 10 4 2 N 2 91,8 10 3 91,8 МПа A1 10 10 4 3 N 3 91,8 10 3 114,8 МПа A2 8 10 4 4 N 4 14,3 10 3 17,9 МПа A2 8 10 4 Строим эпюру (см. рис. 5). Определим деформации каждого участка бруса по формуле: l Nl l ; AE E 0,2 1,6 10 5 м = 0,016 мм; 11 2 10 0,5 l 2 91,8 0,230 мм; 2 10 5 1 l3 114,8 0,574 мм; 2 10 5 l1 16 10 6 7 l 4 17,9 0,3 0,027 мм 2 10 5 Эпюру перемещений строят от жесткой заделки (сечение А). Опора не дает сечению переместиться, поэтому А 0 . Сечение В сместится относительно А на величину l1 B A l1 0,016 мм Сечение С сместится относительно В на величину l2 C B l2 0,016 0,230 0,246 мм Сечение D сместится относительно С на l3 D C l3 0,246 0,574 0,820 мм Сечение Е сместится относительно D на l4 E D l4 0,820 0,027 0,793 мм Смещение сечения Е должно равняться зазору 0,8 мм. Расхождение в значениях, вызванное округлением цифр, не превышающее 5% считается несущественным. При значительных расхождениях надо искать ошибку. Строим эпюру (см. рис. 5). 8 Рисунок 5 Определим, на сколько градусов надо охладить брус, чтобы R 0 . Очевидно, что укорочение стержня из-за охлаждения, должно равняться l R . Удлинение (укорочение) стержня из-за изменения температуры равно: lt lt Поскольку lt lR , то l R 0,16 10 3 t 6,4 град. l 125 107 0,2 0,5 1 0,3 9 ПРИМЕР 2 Для вала (см. рис. 6) следует: 1. определить крутящие моменты Т и построить их эпюру; 2. из условия прочности определить диаметр вала для каждого участка, если 20 МПа; 3. определить углы закручивания и построить эпюру углов поворота сечения от левого крайнего сечения, если G 8 10 4 МПа; 4. указать, отвечает ли вал условию жесткости, если 0,6 град/м. Дано: Р1 = 5 кВт, Р2 = 6 кВт, Р3 = 7 кВт, Р4 = 8 кВт, Р5 = 9 кВт, п = 100 об/мин, l1 = 1,2 м, l2 = 1.0 м, l3 = 1,4 м, l4 = 1,5 м, l5 = 0,8 м. Решение: Поскольку потерями на трение в подшипниках можно пренебречь, то Р0 Р1 Р2 Р3 Р4 Р5 5 6 7 8 9 35 кВт. Определим значения вращающихся моментов по формуле: Т е 9,55 Те Те Р ; п 5 10 3 9,55 477,5 478 Н·м 100 6 10 3 Т е 2 9,55 573 Н·м 100 7 10 3 9,55 668,5 669 Н·м 100 1 3 8 10 3 764 Н·м 4 100 9 10 3 9,55 859 ,5 860 Н·м 100 Т е 9,55 Те 5 Те 0 35 10 3 9,55 3343 Н·м 100 Проверим правильность подсчетов Те Т е1 Т е2 Т е3 Т е4 Т е5 Т е0 478 573 669 764 860 3344 Н·м 10 Небольшое расхождение в значениях вызвано округление цифр. Крутящий момент в сечении численно равен алгебраической сумме всех внешних моментов, действующих на рассматриваемую часть вала. Значения крутящих моментов Т будем определять слева направо. На участке АВ крутящий момент Т1 равен Т1 Т е 478 Н·м. 1 Четкого правила знаков для крутящих моментов нет. Примем Т1, положительным. В этом случае все внешние моменты, направленные как в сечении А, будут считаться положительными. Рисунок 6 11 На участке ВС Ò2 Òå1 Òå2 478 573 1051 Н·м; на участке СD Ò3 Òå Òå Òå 478 573 669 1720 Н·м; 1 2 3 на участке DЕ Ò4 Òå Òå Òå Òå 1720 3343 1623 Н·м; 1 2 3 0 на участке ЕF Ò5 Òå Òå Òå Òå0 Òå 1623 764 859 Н·м. 1 2 3 4 По полученным значениям крутящих моментов строим эпюру Т (см. рис. 6). Диаметр вала для каждого участка определим по формуле: d 3 5T Для участка АB d1 3 5 478 3 119,4 10 2 49,4 мм 50 мм 6 20 10 На участке ВС d2 3 5 1051 3 262,6 10 2 64,2 мм 64 мм 6 20 10 На участке CD d3 3 5 1720 3 429,8 10 2 75,3 мм 75 мм 6 20 10 На участке DE d4 3 5 1623 3 405,9 10 2 72,8 мм 73 мм 6 20 10 На участке EF d5 3 5 859 3 214,9 10 2 60,2 мм 60 мм 6 20 10 Значения d следует округлить до целых чисел. Определим полярный момент инерции сечения для каждого участка вала по формуле: I p 0,1d 4 12 I p1 0,1 50 4 625000 мм4 = 6,2510-7 м4; I p 2 0,1 644 1678000 мм4 = 16,7810-7 м4; I p3 0,1 754 3164000 мм4 = 31,6410-7 м4; I p 4 0,1 734 2840000 мм4 = 28,4010-7 м4; I p5 0,1 604 1296000 мм4 = 12,9610-7 м4. Определим угол закручивания на каждом участке по формуле: 1 AB 180 Tl GI p 180 478 1,2 10,3 104 0,66 3,14 8 10 4 106 6,25 10 7 157 103 град 180 1051 1 0,45 град 3,14 8 1010 16,78 10 7 180 1720 1,4 3 CD 0,56 град 3,14 8 1010 31,64 10 7 180 1623 1,5 4 DE 0,61 град 3,14 8 1010 28,4 10 7 180 859 0,8 5 EF 0,38 град 3,14 8 1010 12,96 10 7 2 BC Знак «минус» у 4 и 5 указывает на то, что закручивание вала на этих участках происходит в противоположную сторону, чем у 1 , 2 и 3 . Эпюру углов закручивания по условию задачи строим от сечения А. Сечение В повернется относительно сечения А на угол ÀÂ = 0,66 град. Сечение С повернется относительно сечения В на угол ÂÑ = 0,45 град., а относительно сечения А на угол АС АВ ВС 0,66 0,45 1,11 град. Сечение D повернется относительно сечения А на угол 13 АD АВ ВС CD 1,11 0,56 1,67 град. Сечения Е и F соответственно на угол повернутся относительно сечения А АЕ АВ ВС CD DE 1,67 0,61 1,06 град. АF АВ ВС CD DE EF 1,06 0,38 0,68 град. На эпюре откладываем значения углов и соединяем их прямыми линиями (см. рис. 6). Определим, отвечает ли вал Относительный угол закручивания равен 1 2 3 4 5 Поскольку соблюдено. 1 l1 2 l2 3 l3 4 l4 5 l5 0,6 условию жесткости. 0,66 0,55 град/м; 1,2 0,45 0,45 град/м; 1,0 0,56 0,40 град/м; 1,4 0,61 0,41 град/м; 1,5 0,38 0,48 град/м. 0,8 град/м условие жесткости вала 14 ПРИМЕР 3 Для заданной балки (см. рис. 7) требуется: 1. Построить эпюры поперечных сил и изгибающих моментов. 2. Из расчета на прочность по нормальным напряжениям подобрать двутавровое, круглое и прямоугольное сечение (положив для прямоугольного сечения отношение высоты к ширине равным двум), если 150 МПа, и сравнить их эффективность. Дано: F = 30 кН, q = 40 кН/м, т = 20 кНм Решение: Определим реакции опор RB и RЕ. Составим уравнения статического равновесия. Моменты, действующие по часовой стрелке, будем считать положительными, против – отрицательными. т В 0 F 2 q 2 1 m RE 4 0 ; 30 2 40 2 1 20 4RE 0 ; RE 10 кН. тE 0 ; F 6 RB 4 q 2 3 m 0 ; 30 6 4 RB 40 2 3 20 0 ; RB 100 кН Проверка: Fy 0 ; F RB q 2 RE 0 ; 30 100 40 2 10 0 ; - 110 + 110 = 0. Реакции определены верно. Определим значения поперечных сил Q и построим их эпюру. Поперечная сила в сечении равна алгебраической сумме всех внешних сил, приложенных к рассматриваемой части балки. На участке АВ: Q1 F 30 кН. Знак «минус» берется потому, что сила F поворачивает рассматриваемую (левую) часть балки против часовой стрелки. 15 Поскольку Q1 не зависит от z, то на участке АВ эпюра представляет собой горизонтальную прямую, пересекающую ось ординат при значении Q = – 30 кН. На участке ВС: Q2 F R B q z 2 2 Q2 30 100 40z2 2 70 40z2 2 Это уравнение наклонной прямой, так как Z2 в первой степени. Ее строим по двум точкам по краям участка: при z2 = 2м Q2 70 402 2 70 кН z2 = 4м Q2 70 404 2 10 кН. Рисунок 7 16 Наклонная прямая на участке ВС пересекла нулевую линию. В точке пересечения изгибающий момент имеет экстремальное значение. Поэтому найдем значение z2, где пересекается нулевая линия: Q2 70 40z2 2 0 ; 70 40 z2 80 0 ; z 2 3,75 м. На участке ED (рассматриваем правую часть балки): Q3 RE 10 кН. Знак «минус» берем потому, что сила RE поворачивает сечение против часовой стрелки. На участке DС: Q4 RE 10 кН. Момент т не учитывается, так как момент представляет собой две равные по величине и противоположно направленные силы. Их проекция на любую ось всегда равна нулю. Поскольку Q3 и Q4 не зависят от z, то на эпюре они представляют горизонтальную прямую со значением ординаты – 10 кН. Эпюра Q построена (см. рис. 7). Проверка: Значения поперечных сил для левой и правой частей балки должны совпасть, если в этом сечении не приложена сосредоточенная сила. Если же сила приложена, то значения Q должны различаться на величину этой силы. В данном примере в сечении С нет сосредоточенной силы и значения Q совпадают. Следовательно, эпюра Q построена правильно. Построим эпюру изгибающих моментов М. Изгибающий момент в сечении численно равен алгебраической сумме всех внешних моментов, вычисленных относительно сечения и приложенных к рассматриваемой части балки. Если внешняя сила или внешний момент поднимают конец балки вверх, то М положительный, опускают – отрицательный. На участке АВ действует только один внешний момент от силы F, равный произведению силы на плечо и стремящийся опустить конец балки А вниз, поэтому М 1 Fz1 30z1 . Это уравнение наклонной прямой. Чтобы провести ее на эпюре М нужно найти две точки по краям участка АВ: 17 z1 = 0 М1 = 0; z1 = 2м М1 = – 60 кНм. На участке ВС действуют три момента: от сил F и RB и от распределенной нагрузки q. Момент от силы RB положительный (поднимает конец балки А вверх), а от распределенной нагрузки q отрицательный (отпускает вниз). Момент от распределенной нагрузки равен произведению q на длину рассматриваемого участка (получаем сосредоточенную силу, действующую посередине рассматриваемого участка) и на половину этой длины (плечо силы). z 2 М 2 Fz2 RB z2 2 qz2 2 2 2 M 2 30 z 2 100 z 2 2 20z 2 2 2 . Раскрывать скобки в уравнении не следует. В таком виде удобнее решать. Это уравнение параболы, так как z2 во второй степени. Параболу строят по двум точкам на краях участка дугой навстречу распределенной нагрузке. Если на этом участке имеется экстремальное значение М (на эпюре Q пересекается нулевая линия), то ищут дополнительно третью точку – экстремальную. В данном примере нужно найти три точки: при z2 = 2м М 2 30 2 100 2 2 202 2 2 60 кНм. z2 = 4м М 2 30 4 100 4 2 204 2 2 0 . z2 = 3,75 м М 2 30 3,75 100 3,75 2 203,75 2 2 1,2 кНм. По полученным точкам строим параболу дугой вверх (см. рис. 7). На участке ED (рассматриваем балку справа), возникает только один момент от силы RЕ, стремящийся поднять конец балки Е вверх (положительный) М 3 RE z3 10z3 . Это уравнение наклонной прямой при z3 = 0 М3 = 0; z3 = 1м М3 = 10 кНм. На участке DС действуют два момента: момент т и момент от силы RЕ, причем момент т стремится опустить конец балки Е вниз (отрицательный) M 4 m RE z 4 20 10 z 4 . Это уравнение наклонной прямой при z4 = 1м М4 = 10 кНм; 18 z4 = 2м М4 = 0. Эпюра М построена (см. рис. 7). Проверка: значения изгибающих моментов для левой и правой частей балки должны совпасть, если в этом сечении не приложен внешний момент. Если же внешний момент приложен, то должны различаться на величину этого момента. В сечении С нет внешнего момента и значения М совпали. Следовательно, эпюра М построена правильно. По эпюре М находят опасное сечение. Им является сечение, где М имеет максимальное значение без учета знака (с точки зрения прочности указанных в примере профилей балки безразлично вверх или вниз происходит изгиб). В данном примере опасное сечение В: М max 60 кНм. Знак «минус» опускается по указанной причине. Сечение выбирают по формуле: Wx Wx 60 10 3 6 M max . 4 10 4 м3 = 400 см3. 150 10 Для двутавра номер проката находят по значению Wх по таблице 1 приложения для № 27 Wх = 371 см3 для № 27а Wх = 407 см30. Двутавр № 27 будет перегружен, так как значение Wх меньше требуемого. Определим процент перегрузки 400 371 100 % = 7,8%. 371 Допускается перегрузка до 5%. Поэтому нужно брать № 27а. Определять процент расхождения в значениях Wх не следует, так как № 27а недогружен. Для круглого сечения Wх 0,1d3. Находим диаметр сечения d 3 10W x 4000 15,9 см. Для прямоугольного сечения bh 2 . Wx 6 19 По условию задачи h = 2b, поэтому b2b 4 b3 ; 6 3 3 3 Wx 3 400 8,45 см 4 4 h 2b 16,9 см. 2 Wx b3 Сравнение 1м веса балки разных профилей можно произвести по площади поперечного сечения. По таблице сортамента (см. табл. 1 приложение А) для двутавра № 27 а находим Аq = 43,2 cм2. Для прямоугольного сечения An bh 8,45 16,9 143 см2. Для круглого сечения Ак d 2 4 3,14 15,9 2 198 см2. 4 Следовательно, самым рациональным из рассматриваемых профилей является двутавр. При использовании круглого сечения Ак 198 расход материала увеличится в 4,6 раза, а при Аq 43,2 использовании прямоугольного сечения в соотношении b 1 в h 2 Аn 143 3,3 раза. Аq 43,2 20 ПРИМЕР 4 Для заданной балки (см. рис. 8) требуется: 1. по характерным точкам построить эпюры Q и M; 2. из условия прочности по нормальным напряжениям подобрать номер двутавра, если 160 МПа; 3. проверить прочность балки по касательным напряжениям, если 80 МПа. Исходные данные: F = 50 кН, q = 40 кН/м; m = 30 кНм. Решение: Определим реакции опор: mB 0 ; F 2 q 2 1 m RD 3 0 50 40 2 30 3RD ; RD 53,3 кН mD 0 ; F 4 RB 3 q 2 2 m 0 50 4 40 4 30 3RB ; RB 23,3 кН Рисунок 8 21 Реакция RB отрицательная, следовательно, сила направлена вниз. Можно сменить направление и знак у RB , а можно оставить направление силы и подставлять отрицательное значение. Остановимся на втором варианте. Проверка: Fy 0 ; F RB q 2 RD 0 ; 50 – 23,3 – 40 2 + 53,3 = 0; 103,3 – 103,3 = 0. Эпюры Q и М будем строить по характерным точкам. Правила построения эпюры Q: 1. На участках с равномерно распределенной нагрузкой эпюра представляет собой наклонную прямую. 2. На участках, свободных от q эпюра представляет горизонтальную прямую. 3. В сечениях, где приложена сосредоточенная сила, эпюра делает скачек на величину этой силы. 4. Внешний момент не влияет на эпюру. 5. В концевых сечениях Q равна сосредоточенной силе, приложенной в этом сечении. Построение эпюры Q производим слева направо. В концевом сечении А Q = F = 50 кН (п. 5). Знак положительный, так как сила поворачивает сечение по часовой стрелке. На участке АВ распределенная нагрузка (п. 2), поэтому эпюра представляет собой горизонтальную линию. В сечении В эпюра делает скачек (п. 3) на величину силы RB . Сила RB фактически направлена вниз и поворачивает сечение против часовой стрелки (отрицательная), поэтому отнимаем ее от значения F QB F RB 50 23,3 26 ,7 кН. Распределенная нагрузка поворачивает сечение против часовой стрелки, поэтому вызывает отрицательную силу Q. Согласно п. 1 на участке ВС эпюра представляет собой наклонную прямую. Определим значение Q в сечении С QС F RB q 2 50 23,3 40 2 53,3 кН На эпюре Q проводим прямую, соединяющую точки QВ и QС. Прямая пересекла нулевую линию. В точке пересечения Q = 0, а М имеет экстремальное значение. Обозначим расстояние от начала q (точка В) до точки пересечения через z и определим его значение. Поперечная сила Qz в этом сечении равна Qz F RB q z 0 22 50 – 23,3 + 40z = 0 z 0,668 м Дальнейшее построение эпюры Q выполняем справа налево. В сечении D Q = – RD = – 53,3 кН (п. 5). Знак «минус» берем потому, что сила RD поворачивает сечение против часовой стрелки. Согласно п. 4 момент m не учитывается. На участке DC эпюра представляет горизонтальную прямую (п. 2). Эпюра Q построена (см. рис. 8). Проверка: Значения Q для левой и правой частей балки должны совпасть, если в этом сечении нет сосредоточенной силы, или различаться на величину силы, если она приложена. В сечении С нет сосредоточенной силы и значения Q совпадают. Построим эпюру М. Правила построения эпюры М по характерным точкам: 1. На участке, где равномерно распределенная нагрузка, эпюра представляет собой параболу дугой навстречу нагрузке. 2. На участке, свободном от распределенной нагрузки, эпюра представляет собой наклонную прямую. В частном случае она может представлять собой горизонтальную прямую (сила Q на этом участке равна нулю). 3. В сечении, где приложен внешний момент, эпюра делает скачек на величину этого момента. 4. В концевых сечениях М = 0, если не приложен внешний момент m, и М = m, если внешний момент приложен. 5. В сечениях, где начинается или заканчивается распределенная нагрузка, если не приложена сосредоточенная сила, эпюра делает плавный переход (сопряжение) от прямой к параболе или наоборот. Если сила приложена, то сопряжения не будет. Это положение соблюдается при выполнении эпюры в масштабе. 6. В сечении, где эпюра Q пересекает нулевую линию, значение М экстремально. Построение эпюры М будем выполнять слева направо. В сечении А М = 0 (п. 4). На участке АВ эпюра представляет собой наклонную прямую (п. 2) МВ = F 1 = 50 кНм. Знак «плюс» взят потому, что сила F поднимает конец балки (не путать с правилом знаков для Q — по часовой стрелке и против). На эпюре М соединяем эти две точки прямой (см. рис. 8). На участке ВС эпюра изображается параболой дугой вверх (п. 1), а в сечении z = 0,668 м имеет максимум (п. 6). Определим МZ в этом сечении 23 M Z F 1 0,668 RB 0,668 q 0,668 0,668 50 1,668 23,3 0,668 2 20 0,668 58,9 кНм. Определим МС M С F 3 RB 2 q 2 1 150 46 ,6 80 53,4 кНм По трем полученным точкам проводим параболу дугой вверх так, чтобы при z = 0,668 м, был максимум (см. рис. 8). Дальнейшее построение эпюры М выполняем справа налево. Согласно п. 4 в сечении D МD = – m = – 30 кНм. Момент m опускает конец балки D вниз, поэтому он отрицательный. На участке DC эпюра представляет собой наклонную прямую (п. 2) M C m RD 1 30 53,3 23,3 кНм. По полученным значениям МD и M C на эпюре М проводим прямую (см. рис. 8). Согласно п. 5 в сечении С должен быть плавный переход от прямой к параболе (при соблюдении масштаба). Эпюра М построена. Проверка: значения М для левой и правой частей балки должны совпасть, если в этом сечении не приложен внешний момент. В сечении С нет внешнего момента. Слева M C 23,4 кНм, справа M C 23,3 кНм. Расхождение в 0,1 кНм вызвано округлением значений реакций опор до 0,1 кН. Если бы округлили до 0,01 кН, то расхождение составило бы 0,01 кНм. Точность до 0,1 кНм вполне достаточна. Эпюра М построена правильно. Примечание: при выполнении задачи 3 в контрольной работе эпюры Q и М можно строить, как показано в примере 3, а можно, как в примере 4. При выполнении эпюр по характерным точкам не следует увлекаться пояснениями и ссылками на пункты правил. Надо давать лишь самые необходимые записи. Подберем двутавровое сечение Wx M max 58,9 103 368 см3 160 Поскольку 1 м = 10 см3, то напряжение можно подставлять в формулу в МПа и результат получится в см3. По таблице сортамента (см. табл. 1 приложения А) находим 3 6 24 № 24 а Wx 317 см3 № 27 Wx 371 см3 Определим процент перегрузки № 24 а 368 317 100% 16,1% , что больше 5%. 317 Берем № 27 с I x 5010 см4, S x 210 см3 и S 6 мм (см. рис. в табл. 1 приложения А, где S — толщина стенки двутавра). Касательные напряжения при поперечном изгибе определяют по формуле Журавского Q Sx , Ix S где для Q берется максимальное значение без учета знака. По эпюре Q находим Q = 53,3 кН, 53,3 103 210 10 6 11,19 8 10 Па = 37,2 МПа 5010 10 8 6 10 3 30,06 Поскольку 80 МПа, прочность двутавровой балки по касательным напряжениям обеспечена. 25 ПРИМЕР 5 Для плоской рамной конструкции (см. рис. 9 а) определить значения внутренних усилий и построить их эпюры. Исходные данные: F = 50 кН, q = 40 кН/м, т = 30 кН м Решение: Определим реакции опор Fx 0 ; q 1 Ax 0 ; Ax 40 кН тA 0 ; F 1 q 1 0,5 m E 2 0 ; 2 E 50 20 30 ; E 30 кН mE 0 ; Ay 2 F 1 q 1 0,5 m 0 ; 2 Ay 50 20 30 ; Проверка: Ay 20 кН. Fy 0 ; Ay F E 0 ; 20 50 30 0 . Определим значения продольных сил N и построим их эпюру. Cилы растяжения считаются положительными, сжатия — отрицательными. Построение эпюры N начинаем со стойки АВ. Рисунок 9 26 Вертикальные стержни называют стойками, горизонтальные — ригелями. Очевидно, что стойку АВ сжимает сила Аy, поэтому на этом участке N = – Ау = – 20 кН. На участок ригеля ВС действует сила Ах, сжимая его. Сила Ау действует поперек ригеля, поэтому не сжимает его и не расстегивает, т. е. не влияет на продольную силу N. Поэтому на этом участке N = -Ах = – 40 кН. Стойку КС рассматриваем снизу. На нее действует лишь распределенная нагрузка q поперек стойки, поэтому N = 0. Стойку ЕD рассмотрим снизу. Ее сжимает сила Е, поэтому N = – Е = = – 30 кН. Часть ригеля DС рассмотрим справа. На нее действует сила Е поперек стержня и момент m, поэтому продольная сила на этом участке равна нулю. Эпюра N построена (см. рис. 9б). Поперечная сила считается положительной, если внешняя сила поворачивает сечение по часовой стрелке и отрицательной — против. Рассмотрим стойку АВ снизу. Поперечную силу вызывает сила Ах, действуя против часовой стрелки, поэтому Q = – Аx = – 40 кН. Сила Ау на стойку АВ действует вдоль оси, поэтому на поперечную силу не влияет. Часть ригеля ВС рассматриваем слева. Поперечную силу в нем вызывает Ау, действующая по часовой стрелке, поэтому Q = Аy = 20 кН. Сила Ах действует вдоль ригеля и на Q не влияет. Стойку КС рассматриваем снизу. Поперечную силу вызывает равномерно распределенная нагрузка q, действующая по часовой стрелке (положительная). Согласно п. 1 примера 4 на участке, где равномерно распределенная нагрузка, эпюра Q изображается наклонной прямой. В точке К Q = 0, в точке С Q = q 1 = 40 кН. Стойку ЕD рассматриваем снизу. На нее действует только сила Е, направленная вдоль стойки, поэтому на участке ЕD Q = 0. Часть ригеля DC рассматриваем справа. На нее действует сила Е против часовой стрелки, поэтому Q = –Е = –30 кН. Эпюра Q показана на рисунке 9 в. Изгибающие моменты откладывают на сжатых волокнах, знаки «плюс» и «минус» не ставят. Стойку АВ рассматриваем снизу. В сечении А изгибающий момент равен нулю (п. 4 правил построения эпюр по характерным точкам). На участке АВ эпюра изображается наклонной прямой (п. 2). В сечении В М В Ах 1 40 кНм. 27 Сила Аy действует вдоль стойки и на М не влияет. Поскольку сила Ах сжимает правые волокна, то значения М на эпюре откладываем справа. Отрезок ригеля ВС рассматриваем слева. На ригель в сечении В действует изгибающий момент МВ = 40 кНм от стойки АВ (соединение в сечении В абсолютно жесткое). Этот момент сжимает нижние слои ригеля, поэтому откладываем его снизу (см. рис. 9 г). На этот отрезок ригеля действует сила Аy, создавая момент, сжимающий верхние слои, поэтому в сечении С эти моменты будут иметь разные знаки. М С лев М В Ау 1 40 20 1 20 кНм. Откладываем значение МС внизу ригеля, так как МВ > Ау 1, следовательно, сжимаются нижние волокна. Стойку КС рассматриваем снизу. В концевом сечении МК = 0 (п. 4 правил построения эпюр М по характерным точкам). На участке КС эпюра изображается параболой навстречу распределенной нагрузке (п. 1 тех же правил). Изгибающий момент в сечении С стойки равен М С с q 1 0,5 40 1 0,5 20 кНм. Поскольку сжимаются левые волокна, параболу строим слева от стойки КС. Стойка ЕD не подвергается изгибу, поэтому изгибающий момент на ней равен нулю. Рассматриваем часть ригеля DC справа. В сечении D действует внешний момент m, сжимающий нижние слои. В сечении С изгибающий момент равен М С пр m E 1 30 30 1 0 . Изгибающий момент от силы Е взят с противоположным знаком, чем m, так как он снимает верхние волокна. Знаки у m и Е можно было взять наоборот. Следует учитывать, что если мы за положительный момент взяли сжимающий нижние волокна, то если в результате вычитания значений моментов, результат получится положительным, то его надо отложить вниз и наоборот, если отрицательный – вверх. Соединим значения МС пр и МD прямой. Эпюра М построена (см. рис. 9 г). Проверка: значения М для левой и правой частей рамной конструкции должны совпасть, если в этом сечении нет внешнего 28 момента; или различаться на величину момента, если он имеется. В сечении С слева МС лев = 20 кНм, МС пр = 0, т. е. значения различаются на величину 20 кН м. В сечении С также действует момент от распределенной нагрузки стойки КС МС с = 20 кНм. 29 УЧЕБНО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ Основная литература 1. Подскребко, М. Д. Сопротивление материалов: учебник / М. Д. Подскребко. – Минск : Выш. шк., 2007. – 797 с. Дополнительная литература 2. Дарков, А. В. Сопротивление материалов: учебник / А. В. Дарков, Г. С. Шпиро. – М. : Высшая школа, 1975. – 639 с. 3. Татур, Г. К. Общий курс сопротивления материалов: учебник / Г. К. Татур. Минск: выш. шк., 1974. – 462 с. Методические пособия 4. Новиков, В. И. Сопротивление материалов: учебнометодическое пособие для студентов-заочников механических специальностей технических вузов / В. И. Новиков, Г. С. Крылов. – Минск: БГПА, 1994. – 131 с. 5. Летковский, Л. И. Сопротивление материалов: курс лекций / Л. И. Летковский. – Барановичи: РИО БарГУ. 2007. – 216 с. 6. Гресс, П. В. Сопротивление материалов: руководство к решению задач / П. В. Гресс. – М. : Высшая школа, 2004. – 158 с. 7. Летковский, Л. И. Механика материалов: пособие по решению задач / Л. И. Летковский. – Барановичи: РИО БарГУ, 2008 – 118 с. 30