Ответы на задания 3 этапа 1.
реклама

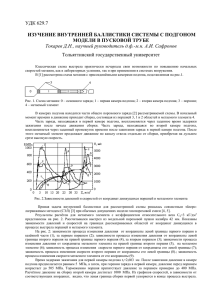
Ответы на задания 3 этапа 1. На рисунке 1 а, б изображены равновесные начальное и конечное положения поршня. Давление p1 , производимое ртутью на верхнюю поверхность поршня (рисунок 1а), складывается из атмосферного p0 , которое на основании закона паскаля передается по объему ртути, и гидростатического ρgh : p1 = p0 + ρgh (1) Ввиду невесомости поршня и одинаковости площадей S его верхней и нижней поверхностей это давление в газе под поршнем. Из уравнения состояния идеального газа, когда налить ртуть, νRT1 (2) p1 = SH где - число молей газа в объеме SH под поршнем; R – газовая постоянная. Приравняв выражения в правых частях равенств (1) (2), получим νRT1 = p0 + ρgh (3) SH Аналогичным образом запишем соотношение νRT2 (4) = p0 S(H + h) Отвечающее верхнему положению поршня (рисунок 1 б), когда ртуть полностью вытеснена из сосуда и атмосферное давление p0 над поршнем уравновешивается давлением в газе, находящемся в объеме S(H + h) при более высокой температуре T2 . T1 (H + h) p0 + ρgh = , T2 H p0 откуда конечная температура p0 H +h T2 = T1 • = 330K H p0 + ρgh а) б) Рисунок – 1 2. При постоянном давлении p работа газа А определяется выражением: (1) A = pV где V - изменение объема. В случае, когда давление газа при изменении объема не остается постоянным, работу газа можно найти, как площадь под зависимостью давления от объема на pV - диаграмме. Определим связь между давлением и объемом в данном случае. Согласно условию T = kp 2 (2) где k - некоторый коэффициент. Воспользуемся теперь уравнением Менделеева – Клайперона m (3) pV = RT μ Подставив в него выражение для температуры согласно (2). Тогда получим следующую связь между давлением и объемом: μ (4) p= V kmR Этому выражению на pV - диаграмме соответствует прямая линия, проходящая через начало координат (рисунок 2). Согласно сказанному в начале решения получаем, что p + p2 A= 1 (V2 _ V1 ) 2 Воспользовавшись выражениями (4) и (2), для работы газа окончательно находим m A= R (T2 _ T1 ) 2 Рисунок – 2 3. На поршень в начальном положении действуют: сила тяжести mg , сила атмосферного давления p0 S , сила давления со стороны газа в цилиндре p1 S и сила упругости пружины kl0 /2 . Из условия равновесия поршня mg+p0S-p1S-kl0/2=0 найдем начальное давление p1 газа под поршнем p1=p0+(mg-kl0/2)/S. Потенциальная энергия пружины и потенциальная энергия поршня в поле сил тяжести изменяется за счет работы A, совершаемой газом в l цилиндре, и работы AАТМ=-p0S 0 сил атмосферного давления: 2 k(l /2) l l ΔE = A + AАТМ или (0- 0 ) + mg 0 = A -p0S 0 . 2 2 2 Отсюда A = (l0 /2)(mg + p0 S -kl0/4)=0,1 кДж. И будет обусловлено работой газа А и работой силы атмосферного давления (-p0SH/2). В результате получаем уравнение: H (M + m)v2 (m - M)gh =A-p0S , + 2 2 2 из которого находим 1 A = ((m+M)v2-(M-m)gH+p0SH))=480 Дж 2 3 4. По первому закону термодинамики: Q = ΔU + A U = 2 5. Из уравнений Клайперона - Менделеева, записанных для газа в состояниях 1 и 2 следует, что эти состояния принадлежат одной изотерме 2p V с температурой T = 0 0 . Так как все промежуточные состояния газа υR лежат на отрезке прямой, расположенной выше указанной изотермы, то максимальная температура газа достигается в одной из этих состояний. Для ее определения запишем уравнение заданного процесса p p=- 0 V + 3p0 V0 Тогда зависимость температуры от объема в процессе 1-2 имеет вид p0 2 3p0 pV V + V T(V)= =RV0 R R Определяя экстремум функции (1), или анализируя график (рисунок 3), находим, что температура газа достигает максимального значения 9p V 3 Tmax = 0 0 при V = V0 4R 2 Рисунок – 3 6. Труба и поршень соскальзывают с наклонной плоскости с одинаковым ускорением a=g(sin -k cos ). (1) На основании второго закона Ньютона запишем уравнение движения поршня (силы, действующие на поршень при соскальзывании трубы, указана на рисунке 4 N – внутренних стенок трубы, p1 и p2 – давления воздуха по обе стороны от поршня): ma=mg sin -(p1-p2)S (2) Исключив из равенств (1) и (2) ускорение а, получим соотношение ( p1 - p2)S=kmg cos (3) На основании закона Бойля-Мариота для воздуха по обеим сторонам поршня: p1V1 = pV (4) p2V2 = pV (5) где V – объем воздуха с каждой стороны поршня в горизонтально лежащей трубе, V1 и V2 – в движущейся трубе (рисунок 4). Из соотношений (3) – (5), образующих вместе с равенством V1 + V2 = 2V систему уравнений, находим отношением объемов (V2 / V1 ) : V2 /V1 = ((kmg cos )/pS) + ((kmgcosα(/pS)2 + 1 = 1,2