5. Содержание отчета Отчет должен содержать: 1) изложение
реклама

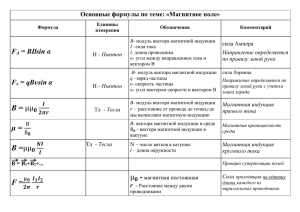
5. Содержание отчета Отчет должен содержать: 1) изложение цели работы; 2) схемы измерений; 3) таблицы измеренных и вычисленных величин; 4) графики построенных зависимостей; 5) выводы. Контрольные вопросы 1. Закон полного тока. Магнитный поток. Закон Фарадея-Максвелла. Экранирование электростатических полей. Скин-эффект. Глубина скин-слоя. 7. Выбор материалов для изготовления экранов. Ответ иллюстрировать графиками измеренных частотных зависимостей коэффициентов экранирования. 8. В каком диапазоне частот труднее экранировать помехи? Литература 1. Аполлонский СМ. Справочник по расчету электромагнитных экранов. - Л.: Энергоатомиздат, 1988. Зильберман Г.Е. Электричество и магнетизм. - М.: Наука, 1970. Терлеццкий Я.П., Рыбаков Ю.П. Электродинамика. - М.: Высшая школа, 1980. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. -М.: Наука, 1992. 5. Справочник технолога-приборостроителя: В 2-х т. - Под ред. Е.А.Скороходова. - М.: Машиностроение, 1980. Лабораторная работа № 4 Исследование магнитного поля цилиндрической катушки -3- Работа 4 ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ ЦИЛИНДРИЧЕСКОЙ КАТУШКИ Цель работы: измерение составляющих вектора магнитной индукции поля круглой цилиндрической катушки с током. 4.1. Основные теоретические положения Цилиндрические катушки широко применяются во многих электроизмерительных приборах, электрических машинах, установках для высокочастотного нагрева металлов и диэлектриков, в лабораторной практике и др. Во всех перечисленных примерах интерес представляют величина и распределение в пространстве вектора магнитной и индукции В (или вектора напряженности магнитного поля Н). Уравнения Максвелла для магнитного поля постоянного тока имеют вид гotH J ; divB 0, 4.1 где J - вектор плотности тока проводимости. Такой же вид имеют эти уравнения и для переменного тока низкой частоты, когда можно пренебречь токами смещения. В общем случае расчет распределения вектора В вокруг контура с током сводится к решению уравнений (4.1) при известных граничных условиях: Bп1 Bп2 H 2 H 1 ; 4.2 4.3 где Bп1 , Bп2 – нормальные составляющие ректора В ; H 1 , H 2 – касательные составляющие вектора Н на границе раздела двух сред 1,2; К – модуль вектора поверхностной плотности тока. Направление вектора К совпадает с касательным вектором t , перпендикулярным вектору (рис.4.1).