Алгебра 10 класс (70 ч ) ( 2 ч. ... Учебник «Алгебра и начала анализа» Мордкович А.Г.Москва , «Мнемозина» 2007

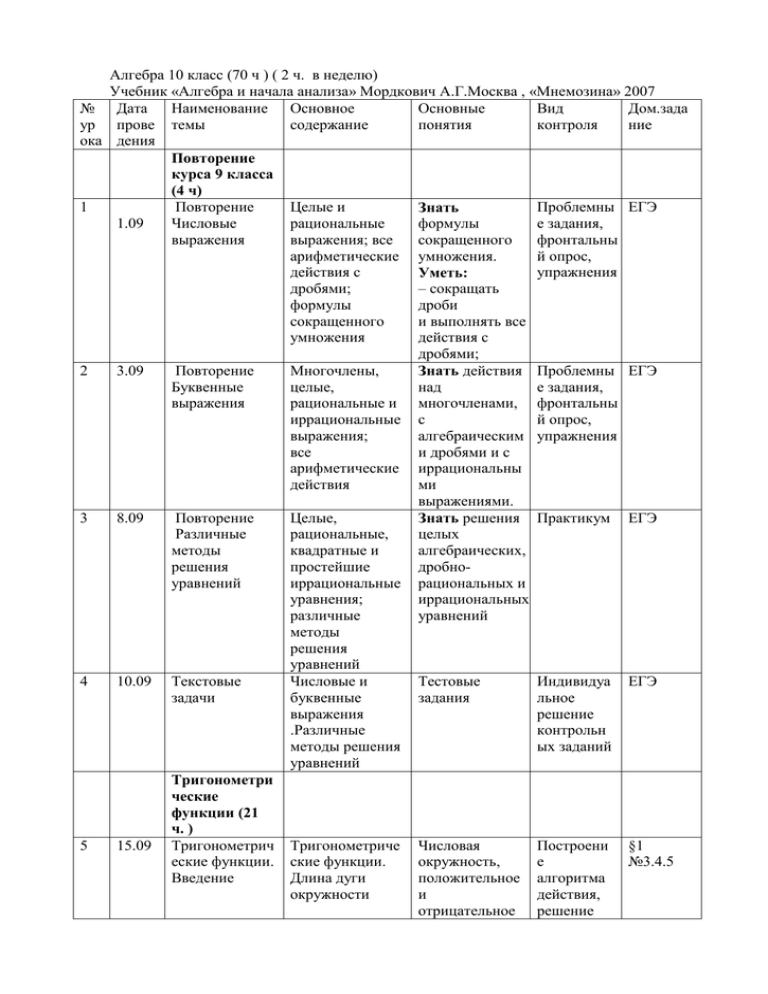
Алгебра 10 класс (70 ч ) ( 2 ч. в неделю)
Учебник «Алгебра и начала анализа» Мордкович А.Г.Москва , «Мнемозина» 2007
№ Дата
Наименование Основное
Основные
Вид
Дом.зада
ур прове темы
содержание
понятия
контроля
ние
ока дения
Повторение
курса 9 класса
(4 ч)
1
Повторение
Целые и
Проблемны ЕГЭ
Знать
1.09
Числовые
рациональные
формулы
е задания,
выражения
выражения; все
сокращенного
фронтальны
арифметические умножения.
й опрос,
действия с
упражнения
Уметь:
дробями;
– сокращать
формулы
дроби
сокращенного
и выполнять все
умножения
действия с
дробями;
2
3.09
Повторение
Многочлены,
Знать действия Проблемны ЕГЭ
Буквенные
целые,
над
е задания,
выражения
рациональные и многочленами, фронтальны
иррациональные с
й опрос,
выражения;
алгебраическим упражнения
все
и дробями и с
арифметические иррациональны
действия
ми
выражениями.
3
8.09
Повторение
Целые,
Знать решения Практикум ЕГЭ
Различные
рациональные,
целых
методы
квадратные и
алгебраических,
решения
простейшие
дробноуравнений
иррациональные рациональных и
уравнения;
иррациональных
различные
уравнений
методы
решения
уравнений
4
10.09 Текстовые
Числовые и
Тестовые
Индивидуа ЕГЭ
задачи
буквенные
задания
льное
выражения
решение
.Различные
контрольн
методы решения
ых заданий
уравнений
Тригонометри
ческие
функции (21
ч. )
5
15.09 Тригонометрич Тригонометриче Числовая
Построени §1
еские функции. ские функции.
окружность,
е
№3.4.5
Введение
Длина дуги
положительное алгоритма
окружности
и
действия,
отрицательное решение
6
17.09
Числовая
окружность
Система
координат,
числовая
окружность.
Макеты
числовой
окружности
7
22.09
Числовая
окружность на
координатной
плоскости
Числовая
окружность на
координатной
плоскости
8
24.09
Синус
и косинус
Синус, косинус
и их свойства,
первая, вторая,
третья и
четвертая
четверти
окружности
9
29.09
10
1.10
Вводный
контроль
Синус
и косинус
Вводный
контроль
Синус, косинус
и их свойства,
первая, вторая,
третья и
четвертая
четверти
окружности
11
6.10
Тангенс
Простейшие
направление
обхода
окружности
Числовая
окружность,
положительное
и
отрицательное
направление
обхода
окружности
Знать, как
определить
координаты
точек числовой
окружности.
Уметь:
– составить
таблицу для
точек числовой
окружности и
их координат;
– по
координатам
находить точку
числовой
окружности;
Знать понятие
синуса,
косинуса,
произвольного
угла;
радианную
меру угла.
Уметь:
– вычислить
синус, косинус
числа;
Вводный
контроль
Знать понятие
синуса,
косинуса,
произвольного
угла;
радианную
меру угла.
Уметь:
– вычислить
синус, косинус
числа;
Решение
упражнени
й, ответы
на вопросы
Построени
е
алгоритма
действия,
решение
упражнени
й, ответы
на вопросы
Проблемн
ые задания,
индивидуа
льный
опрос
Фронтальн
ый опрос;
работа
с
демонстрац
ионным
материало
м
Контрольн
ая работа
Проблемн
ые задания,
фронтальн
ый опрос,
упражнени
я
Практикум
§2
№9-16 (г
)
§3
№35.37,
42 (а), 43
(а, в)
§4
№55(а,
г).56,
58(а,
б),60.73
(а, б)
§4
№63, 64,
74(а,
б),76(а, г)
,83
§5
и котангенс
тригонометричес простейших
кие уравнения
тригонометрич
еских
уравнений с
помощью
числовой
окружности
Тангенс,
Знать понятие
котангенс и их
тангенса,
свойства, первая, котангенса
вторая, третья и произвольного
четвертая
угла;
четверти
радианную
окружности
меру угла.
Уметь:
– вычислить
тангенс и
котангенс
числа;
– вывести
некоторые
свойства
тангенса,
котангенса;
Тригонометриче Уметь:
ские функции
– совершать
числового
преобразования
аргумента,
простых
тригонометрич
еских
выражений
Синус угла,
Знать, как
косинус угла,
вычислять
тангенс угла,
значения
котангенс
синуса,
косинуса,
тангенса и
котангенса
градусной и
радианной
меры угла,
используя
табличные
значения
12
8.10
Тангенс
и котангенс
13
13.10
Тригонометрич
еские функции
числового
аргумента
14
15.10
Тригонометрич
еские функции
углового
аргумента
15
16
20.10
22.10
Резерв времени
Определение
Определение
Контрольная
работа № 1 по тригонометриче тригонометри
ских функций
ческих функций
теме
«Определение
тригонометри
ческих
функций»
№87, 88,
89(а,
б),90(а, б)
Практикум,
фронтальн
ый опрос,
упражнени
я
§5
№97,
96(а,
б),95(а, б)
ЕГЭ
Построени
е
алгоритма
действия,
решение
упражнени
й
Проблемн
ые задачи,
фронтальн
ый опрос,
упражнени
я
§6
№111,
112(а,
б),116(а)
,118(б),
Индивидуа
льное
решение
контрольн
ых заданий
§ 1-7
ЕГЭ
§7
№143,
145
17
27.10
Формул
приведения
Формулы
приведения,
углы перехода
18
29.10
Функция
y = sin x, ее
свойства
и график
19
10.11
Функция
y = cos x, ее
свойства
и график
Тригонометриче
ская функция
y = sin x, график
функции,
свойства
функции
Тригонометриче
ская функция, y
= сos x, график
функции,
20
12.11
21
17.11
22
19.11
23
24.11
Знать вывод
формул
приведения.
Уметь:
– упрощать
выражения,
используя
основные
тригонометрич
еские
тождества и
формулы
приведения;
Алгоритм
применения
формул
приведения
Знать
тригонометрич
ескую
функцию y =
sin x, ее
свойства и
построение
графика
Периодичность Тригонометриче Знать
функций y = sin ская функция, y
тригонометрич
x,
= сos x, график
ескую
y = cos x
функции,
функцию y =
cos x, ее
свойства и
построение
графика
Периодичность Периодическая
Знать о
функций y = sin функция, период периодичности
x,
функции,
и основном
y = cos x
основной период периоде
функций
y = sin x и y =
cos x.
Как построить Растяжение от
Уметь:
график
оси абсцисс,
– график y =
функции
сжатие к оси
f(x) вытянуть и
y = mf(x),
абсцисс,
сжать от оси
если известен
построение
OX в
график
графика
зависимости от
функции
функции
значения m
y = f(x)
y = mf(x)
Как построить Сжатие
Уметь:
график
к оси ординат,
– график y =
Составлени § 8
е опорного № 162,
конспекта, 164
ответы на
вопросы
Самостоя
тельная
работа
§9
№
165,166
Решение
упражнени
й,
составлени
е опорного
конспекта,
ответы на
вопросы
Составлени
е опорного
конспекта,
решение
задач,
работа с
тестом и
книгой
Проблемн
ые задачи,
фронтальн
ый опрос,
упражнени
я
§ 10
№
172,174(б
),
175(б),17
6 (а)
Решение
упражнени
й; ответы
на вопросы
§ 12
№ 235 (
б), 230,
236(б)
Решение
упражнени
§ 13
№ 239 ,
§11
№ 203
(б),204
(б),
205(б)
§ 11
№
217,218,2
20
функции
y = f(kx),
если известен
график
функции
y = f(x)
График
гармоническог
о колебания
24
26.11
25
1.12
Функции
y = tg x,
y = ctg x,
их свойства
и графики
26
3.12
27
8.12
Контрольная
работа № 2 по
теме
«Свойства и
графики
тригонометри
ческих
функций»
Тригонометри
ческие
уравнения (8 ч
)
Первые
представления о
решении
тригонометриче
ских уравнений
28
10.12
Арккосинус .
Решение
уравнения
cos t = a
29
15.12
Арксинус,
растяжение от
оси ординат,
преобразование
симметрии
относительно
оси ординат
Закон
гармонических
колебаний,
частота
колебаний,
амплитуда,
начальная фаза
f(x) вытянуть и
сжать от оси
OX в
зависимости от
значения m;
й,
составлени
е опорного
конспекта,
ответы на
вопросы
Работа
с
демонстрац
ионным
материало
м
240,
241(а, г)
Фронтальн
ый опрос;
работа
с
демонстрац
ионным
материало
м
Индивидуа
льное
решение
контрольн
ых заданий
§ 15
№ 261 ,
262( а, б
), 263 (б)
Уметь:
– решать
простейшие
тригонометрич
еские
уравнения по
формулам;
Решение
проблемны
х задач
§ 16
№284,
285
Знать
определение
арккосинуса.
Уметь:
– решать
простейшие
уравнения
сos t = a;
Знать
Проблемны
е
задания;
составление
опорного
конспекта
§ 17
№ 293,
294,295
(а, г)
Проблемн
§18
Знать формулу
гармонических
колебаний.
Иметь
представление
о графике
гармонических
колебаний
Тригонометриче Знать
ские функции:
тригонометрич
y = tg x,
ескую
y = ctg x, график функцию y = tg
функций,
x, y = ctg x, ее
свойства
свойства и
функций
построение
графика
Свойства и
Свойства и
графики
графики
тригонометриче тригонометри
ских функций
ческих функций
Тригонометриче
ские уравнения,
графический
метод решения
уравнений вида
cos x = α,
sin x = α,
tg x = α,
ctgt= α
Арккосинус,
уравнение
сos t = α,
неравенства
cos t > α,
простейшие
тригонометричес
кие уравнения
Арксинус,
§ 14
№ 250 ,
252( а)
§ 9-15
ЕГЭ
уравнение sin t
=α
уравнение sin t =
α, неравенства
sin t > α,
простейшие
тригонометричес
кие уравнения
Арктангенс и
арккотангенс,
урав-нения:
tg t = a.
ctg x = a
30
17.12
Арктангенс и
арккотангенс,
уравнения:
tg t = a.
ctg t = a
31
32
22.12
24.12
Резерв времени
Тригонометрич
еские
уравнения
33
29.12
Тригонометрич
еские
уравнения
34
35
Контрольная
работа № 3 по
теме
«Тригонометр
ические
уравнения»
Простейшие
тригонометричес
кие уравнения,
метод введения
новой
переменной,
метод
разложения на
множители,
определение
арксинуса.
Уметь:
– решать
простейшие
уравнения
sin t = a;
Умение
строить график
арктангенса,
арккотангенса
и решать
неравенства tg t
> a и ctg t > a.
ые задачи;
построение
алгоритма
действия,
решение
упражнени
й
Решение
упражнени
й,
составлени
е опорного
конспекта
№313 (а,
г)
Уметь:
– решать
простейшие
тригонометриче
ские уравнения
по формулам;
Практикум
,фронтальн
ый опрос;
демонстрац
ия слайдлекции
§20
№350 (а,
г), 352,
354
Проблемн
ые задачи,
фронтальн
ый опрос,
упражнени
я
§20
№360 (а,
г), 362,
366 (а)
Индивидуа
льное
решение
контрольн
ых заданий
§16-20
ЕГЭ
Работа с
§ 21
Уметь:
– решать
Однородные
тригонометрич
тригонометричес
еские
кие уравнения,
уравнения
алгоритм
методом
решения
замены
однородного
переменной,
уравнения
методом
второй степени
разложения на
множители;
Тригонометриче Однородные
ские уравнения
тригонометри
ческие
уравнения,
алгоритм
решения
однородного
уравнения
второй
степени
Преобразован
ие
тригонометри
ческих
выражений (
14 ч)
Синус и косинус Формулы синуса
Знать формулу
§19
№335 (а,
г), 336,
343
суммы
аргументов
и косинуса
суммы
аргументов,
вывод формул
Формулы синуса
и косинуса
разности
аргументов,
вывод формул
синуса,
косинуса
суммы углов.
опорными №404,
конспектам 401, 402,
и
405
Знать формулу
синуса,
косинуса
разности двух
углов.
Уметь:
–
преобразовыва
ть простейшие
выражения,
используя
основные
тождества,
формулы
приведения;
Знать формулу
синуса,
косинуса
разности двух
углов.
Уметь:
–
преобразовыва
ть простейшие
выражения,
используя
основные
тождества,
формулы
приведения;
Знать формулу
тангенса и
котангенса
суммы и
разности двух
углов.
Практикум
,фронтальн
ый опрос;
решение
упражнени
й,
составлени
е опорного
конспекта
§ 22
№419,
422
Практикум
§ 22
№427,
430,439
ЕГЭ
Фронтальн
ый опрос;
решение
качественн
ых задач
§ 23
№443,444
36
Синус и
косинус
разности
аргументов
37
Синус и
косинус
разности
аргументов
Формулы синуса
и косинуса
разности
аргументов,
вывод формул
38
Тангенс суммы
и разности
аргументов
Формулы
тангенса
разности и
суммы
аргументов
39
Контрольная
работа по
теме
«Тригонометр
ические
функции
сложения
аргументов»
Формулы
двойного
угла
Тригонометрич
еские формулы
сложения
аргументов
Тригонометри
ческие
формулы
сложения
аргументов
Индивидуа § 21- 23
льное
ЕГЭ
решение
контрольн
ых заданий
Формулы
двойного
аргумента,
Знать
формулы
двойного угла
Построени
е
алгоритма
40
§ 24
№465,467
.473
формулы
половинного
угла, формулы
кратного
аргумента
синуса,
косинуса и
тангенса.
Уметь:
– применять
формулы для
упрощения
выражений;
действия,
решение
упражнени
й
ЕГЭ
41
Формулы
двойного
угла
Формулы
двойного
аргумента,
формулы
половинного
угла, формулы
кратного
аргумента
Знать
формулы
двойного угла
синуса,
косинуса и
тангенса.
Уметь:
– применять
формулы для
упрощения
выражений;
Построени
е
алгоритма
действия,
решение
упражнени
й
§ 24
№464,466
.472
ЕГЭ
42
Формулы
понижения
степени
Формулы
половинного
угла, формулы
понижения
степени
Знать
формулы
понижения
степени синуса,
косинуса
и тангенса.
§ 25
№507,505
.509
43
Преобразовани
е сумм
тригонометрич
еских функций
в произведение
Уметь:
–
преобразовывать
суммы
тригонометричес
ких функций
в произведение;
простые
тригонометричес
кие выражения;
Построени
е
алгоритма
действия,
решение
упражнени
й
Работа с
опорными
конспектам
и,
раздаточны
м
материало
м
44
Преобразовани
е сумм
тригонометрич
еских функций
в произведение
Уметь:
–
преобразовыва
ть суммы
тригонометрич
еских функций
в
произведение;
простые
тригонометрич
еские
выражения;
– обосновывать
суждения,
давать
определения,
приводить
Уметь:
Уметь:
–
–
преобразовывать преобразовыва
суммы
ть суммы
тригонометричес тригонометрич
ких функций
еских функций
в произведение; в
§ 26
№526,527
.533
Работа с
§ 26
опорными №525,528
конспектам .532
и,
раздаточны
м
материало
45
46
47
48
49
Преобразовани
е произведений
тригонометрич
еских функций
в сумму
простые
произведение;
тригонометричес простые
кие выражения;
тригонометрич
еские
выражения;
– обосновывать
суждения,
давать
определения,
приводить
Формулы
Знать, как
преобразования преобразовыва
произведения
ть
тригонометричес произведения
ких функций в
тригонометрич
сумму
еских функций
в сумму;
м
Работа с
опорными
конспектам
и,
раздаточны
м
материало
м
Преобразование Вспомогательны Знать формулу Фронтальн
выражения Asin й аргумент,
перехода от
ый опрос;
x+
преобразование
суммы двух
работа
+ Bcos x к виду выражений Аsin функций с
со слайдCsin(x + t)
x+
различными
лекцией
+ Bcos x
коэффициента
«Преобраз
к виду Сsin(x +
ми в одну из
ование
t)
тригонометрич выражений
еских функций. »
Зачет по теме
Преобразование Знать о
Опрос по
«Преобразовани тригонометричес преобразовани теоретичес
е
ких выражений
и
кому
тригонометриче
тригонометрич материалу;
ских
еских
построение
выражений»
выражений,
алгоритма
применяя
решения
различные
задания
формулы
Преобразование Преобразование Индивидуа
Контрольная
работа по теме тригонометричес тригонометриче льное
ких выражений
ских выражений решение
№ 5 по теме «
контрольн
Формулы
ых заданий
тригонометри
и»
Производная
( 10 ч)
Предел
Предел функции Знать понятие Фронтальн
функции
на
о пределе
ый опрос,
бесконечности,
функции на
демонстрац
предел функции бесконечности ия слайдв точке,
и в точке.
лекции
непрерывная
Уметь:
функция на
– посчитать
промежутке,
приращение
§ 27
№555,558
.560
§ 28
№569,574
§ 21- 28
№570,576
ЕГЭ
§ 21- 28
§ 31
№670,673
окрестность
точки,
приращение
аргумента,
приращение
функции
Задача о
скорости
движения,
мгновенная
скорость,
касательная к
плоской кривой,
касательная к
графику
функции,
производная
функции
Формулы
дифференцирова
ния, правила
дифференцирова
ния
аргумента и
функции;
вычислить
простейшие
пределы;
50
Определение
производной
51
Вычисление
производной
52
Вычисление
производной
Формулы
дифференцирова
ния, правила
дифференцирова
ния
53
Контрольная
работа № 6 по
теме «Правила
дифференциро
вания »
Уравнение
касательной к
графику
функции
54
Знать понятие
о производной
функции
Работа
§ 32
с
№716,714
опорными
конспектам
и
Уметь:
– находить
производные
суммы,
разности,
произведения,
частного;
производные
основных
элементарных
функций;
Проблемн
ые задачи,
индивидуа
льный
опрос
§ 33
№737,739
, 745,747
Практикум
§ 33
№778,783
, 772
Правила и
формулы
отыскания
производных
Уметь:
– находить
производные
суммы,
разности,
произведения,
частного;
производные
основных
элементарных
функций
Правила и
формулы
отыскания
производных
§ 31-33
ЕГЭ
Касательная
к графику,
угловой
коэффициент,
алгоритм
составления
Уметь:
– составлять
уравнения
касательной к
графику
функции по
Индивидуа
льное
решение
контрольн
ых заданий
Фронтальн
ый опрос;
демонстрац
ия слайдлекции
§ 34
№814,825
, 826
55
Применение
производной
для
исследования
функций
на
монотонность
и экстремумы
56
Применение
производной
для отыскания
наибольших и
наименьших
значений
величин
57
Выходной
контроль
Задачи на
отыскание
наибольших и
наименьших
значений
величин
Контрольная
работа № 7 по
теме
«Применение
производной к
исследованию
функции»
Повторение
( 11 ч)
Свойства
тригонометрич
еских функций
58
59
60
уравнения
касательной к
графику
функции
Возрастающая и
убывающая
функция на
промежутке,
монотонность,
точки
экстремума,
алгоритм
исследования
функции на
монотонность и
экстремумы
Нахождение
наибольшего и
наименьшего
значений
непрерывной
функции
на промежутке,
алгоритм
нахождения
наименьшего и
наибольшего
значений
непрерывной
функции на
отрезке
Выходной
контроль
Задачи на
отыскание
наибольших и
наименьших
значений
величин
Применение
производной к
исследованию
функции
алгоритму;
Уметь:
– исследовать
простейшие
функции на
монотонность
и на
экстремумы,
строить
графики
простейших
функций;
Фронтальн § 35
ый опрос;
№856,861
демонстрац
ия слайдлекции
Уметь:
– исследовать
в простейших
случаях
функции на
монотонность,
находить
наибольшие и
наименьшие
значения
функций;
Проблемн
ые задачи,
фронтальн
ый опрос;
составлени
е
конспекта,
решение
задач
Выходной
контроль
Задачи на
отыскание
наибольших и
наименьших
значений
величин
Применение
производной к
исследованию
функции
Контрольн
ая работа
Практикум
Индивидуа
льное
решение
контрольн
ых заданий
Свойства и
Преобразование Практикум
графики
тригонометриче
тригонометриче ских выражений
ских функций
§ 36
№936,939
,941
§ 36
№950,953
§ 32-36
№196,197
,260
ЕГЭ
61
Тригонометрич
еские
уравнения
62
Преобразовани
е
тригонометрич
еских
выражений
Преобразовани
е
тригонометрич
еских
выражений
Производная
63
64
65
66
Исследование
функции с
помощью
производной
Исследование
функции с
помощью
производной
Однородные
тригонометричес
кие уравнения,
алгоритм
решения
однородного
уравнения
второй степени
Преобразование
тригонометричес
ких выражений
Преобразование Практикум
тригонометриче
ских выражений
Преобразовани Практикум
е
тригонометрич
еских
выражений
Преобразование Преобразование Практикум
тригонометричес тригонометриче
ких выражений
ских выражений
Формулы
дифференцирова
ния, правила
дифференцирова
ния
Нахождение
наибольшего и
наименьшего
значений
непрерывной
функции
на промежутке,
алгоритм
нахождения
наименьшего и
наибольшего
значений
непрерывной
функции на
отрезке
Нахождение
наибольшего и
наименьшего
значений
непрерывной
функции
на промежутке,
алгоритм
Уметь:
– находить
производные
суммы,
разности,
произведения,
частного;
производные
основных
элементарных
функций
Графики
Практикум
№356,357
ЕГЭ
№427,428
,430,ЕГЭ
№772,774
, ЕГЭ
Практикум
ЕГЭ
Уметь:
– исследовать
в простейших
случаях
функции на
монотонность,
находить
наибольшие и
Практикум
№871,873
ЕГЭ
67
Исследование
функции с
помощью
производной
68
Исследование
функции с
помощью
производной
69
Исследование
функции с
помощью
производной
нахождения
наименьшего и
наибольшего
значений
непрерывной
функции на
отрезке
Нахождение
наибольшего и
наименьшего
значений
непрерывной
функции
на промежутке,
алгоритм
нахождения
наименьшего и
наибольшего
значений
непрерывной
функции на
отрезке
Нахождение
наибольшего и
наименьшего
значений
непрерывной
функции
на промежутке,
алгоритм
нахождения
наименьшего и
наибольшего
значений
непрерывной
функции на
отрезке
Нахождение
наибольшего и
наименьшего
значений
непрерывной
функции
на промежутке,
алгоритм
нахождения
наименьшего и
наибольшего
значений
непрерывной
функции на
отрезке
наименьшие
значения
функций;
Уметь:
– исследовать
в простейших
случаях
функции на
монотонность,
находить
наибольшие и
наименьшие
значения
функций;
ЕГЭ
ЕГЭ
Уметь:
– исследовать
в простейших
случаях
функции на
монотонность,
находить
наибольшие и
наименьшие
значения
функций;
ЕГЭ
ЕГЭ
Уметь:
– исследовать
в простейших
случаях
функции на
монотонность,
находить
наибольшие и
наименьшие
значения
функций;
ЕГЭ
ЕГЭ
70
Исследование
функции с
помощью
производной
Нахождение
наибольшего и
наименьшего
значений
непрерывной
функции
на промежутке,
алгоритм
нахождения
наименьшего и
наибольшего
значений
непрерывной
функции на
отрезке
Уметь:
– исследовать
в простейших
случаях
функции на
монотонность,
находить
наибольшие и
наименьшие
значения
функций;
Практикум
№871,873
ЕГЭ