Урок обобщающего повторения на тему: « Центральные и вписанные углы.»
реклама
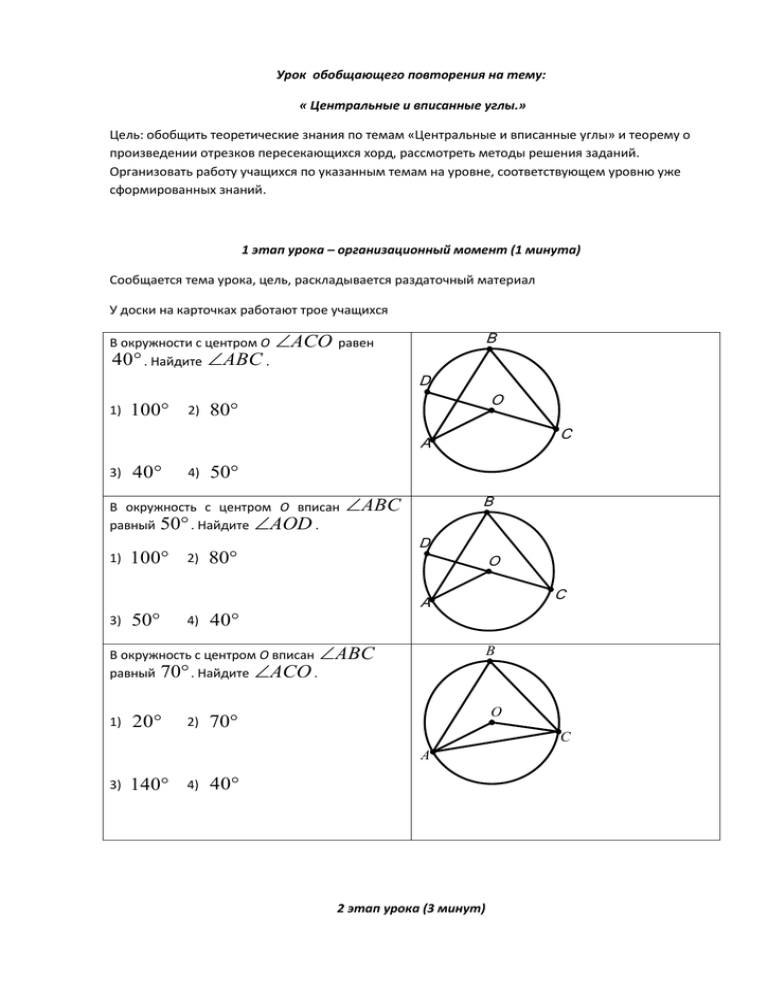
Урок обобщающего повторения на тему: « Центральные и вписанные углы.» Цель: обобщить теоретические знания по темам «Центральные и вписанные углы» и теорему о произведении отрезков пересекающихся хорд, рассмотреть методы решения заданий. Организовать работу учащихся по указанным темам на уровне, соответствующем уровню уже сформированных знаний. 1 этап урока – организационный момент (1 минута) Сообщается тема урока, цель, раскладывается раздаточный материал У доски на карточках работают трое учащихся В окружности с центром O 40 . Найдите ABC . ACO B равен D 1) 100 2) O 80 C A 3) 40 4) 50 В окружность с центром O вписан равный 50 . Найдите AOD . ABC B D 1) 100 2) 80 O C A 3) 50 4) 40 В окружность с центром O вписан ABC равный 70 . Найдите ACO . 1) 20 2) B O 70 C A 3) 140 4) 40 2 этап урока (3 минут) Повторение теоретического материала по теме «Центральные и вписанные углы» 1) Какой угол называется центральным углом окружности? 2) Объясните какая дуга называется полуокружностью, какая дуга меньше полуокружности, а какая больше полуокружности. 3) Как определяется градусная мера дуги? Как она обозначается? 4) Какой угол называется вписанным? Сформулируйте теорему о вписанном угле. 5) Что вы знаете о вписанных углах, опирающихся на одну и туже дугу, опирающийся на полуокружность 3 этап урока (5 минут) Устная работа по решению простейших задач на тему «Центральные и вписанные углы» Учитель предлагает учащимся применить только что сформулированные теоретические факты к решению задач. Учащимся розданы листы с заданиями для устной работы, следующего содержания: Найди х №1 №2 №3 №4 №5 №6 №7 №8 №10 №9 №12 №11 Учащиеся по очереди отвечают на формулированные вопросы, комментируя свой ответ ссылкой на соответствующий теоретический факт. Проверка работ по карточкам . 4 этап урока (15 минут) Решение задач № 668.Докажите, что перпендикуляр, проведенный из какой –нибудь точки окружности к диаметру, есть среднее пропорциональное для отрезков, на которые основание перпендикуляра делит диаметр. Решение 1) АСВ – вписанный и опирается на полуокружность, следовательно, АСВ = 90°. 2) СD = АD ВD . № 670.Через точку А проведены касательные АВ( В- точка касания) и секущая, которая пересекает окружность в точках P и Q. Докажите , что AB2 = AP · AQ. Решение 1) и АВР АВР = 1 2 = 1 2 BP. АQВ = 2) АВР (угол А – общий и 3) ВР АQB АQВ, так как (задача № 664) по АВР = АQB). двум углам АВ AP AQ AB , значит AB2 = AP · AQ. 5 этап урока(10 минут) Разноуровневая самостоятельная работа Учитель выдает задания для самостоятельной работы, сообщая учащимся, что на ее выполнение отводится 15 минут. Трое учащихся (с1,2,3 уровня) работают на доске. 1 уровень 1. Точки А, В, С лежат на окружности с центром О, АС : АОВ = 80°, = 2 : 3. Найдите углы треугольника АВС. ВС = 2. Хорды АВ и СD пересекаются в точке K, причем хорда АВ делится точкой К на отрезки, равные 10 см и 6 см. На какие отрезки точка K делит хорду СD, если СD > АВ на 3 см? 2 уровень 1. Вершины треугольника АВС лежат на окружности с центром О (см. рис. к задаче 1 I варианта), АВС = 80°, ВС : АВ = 3 : 2. Найдите углы треугольника АОВ. 2. Хорды MN и KL пересекаются в точке А, причем хорда MN делится точкой А на отрезки, равные 1 см и 15 см. На какие отрезки точка А делит хорду KL, если KL в два раза меньше MN? 3 у р о в е н ь (для более подготовленных учащихся) 1. Окружность с центром О касается сторон АВ, ВС, АС треугольника АВС соответственно в точках K, M, N, KМ : MN : NK = 6 : 5 : 7. Найдите углы треугольника АВС. 2. Хорды АВ, СD, EF окружности с центром О попарно пересекаются в точках K, М, N, причем каждая хорда делится этими точками на равные части. Найдите периметр треугольника KMN, если АВ = 12 см. 6 этап урока (5 минут) Обсуждение решений задач представленных на доске. Учащиеся , выполнявшие задачи у доски, комментируют свои решения, а остальные вносят , при необходимости коррективы. 7 этап урока(1 минута) Подведение итогов урока. Учитель еще раз обращает внимание, на типы задач и те теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их. Отмечает наиболее успешных учащихся, выставляет отметки




