файл в формате Winword 6.0 (kolm2w6, 179705b)

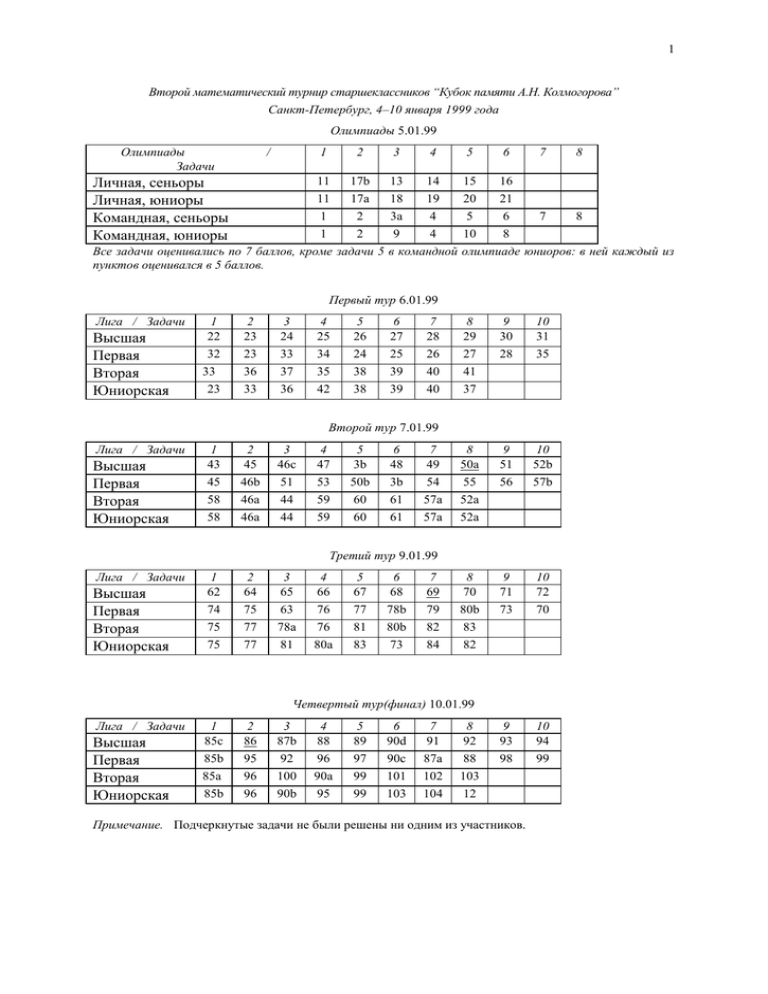
1
Второй математический турнир старшеклассников “Кубок памяти А.Н. Колмогорова”
Санкт-Петербург, 4–10 января 1999 года
Олимпиады 5.01.99
Олимпиады
Задачи
/
1
2
Личная, сеньоры
Личная, юниоры
Командная, сеньоры
Командная, юниоры
11
17b
11
17a
1
2
1
2
Все задачи оценивались по 7 баллов, кроме задачи 5
пунктов оценивался в 5 баллов.
3
4
13
14
18
19
3a
4
9
4
в командной
5
6
7
15
16
20
21
5
6
7
8
10
8
олимпиаде юниоров: в ней каждый из
Первый тур 6.01.99
Лига / Задачи
Высшая
Первая
Вторая
Юниорская
1
22
32
33
23
2
23
23
36
33
3
24
33
37
36
4
25
34
35
42
5
26
24
38
38
6
27
25
39
39
7
28
26
40
40
8
29
27
41
37
9
30
28
10
31
35
8
50a
55
52a
52a
9
51
56
10
52b
57b
8
70
80b
83
82
9
71
73
10
72
70
9
93
98
10
94
99
Второй тур 7.01.99
Лига / Задачи
Высшая
Первая
Вторая
Юниорская
1
43
45
58
58
2
45
46b
46a
46a
3
46c
51
44
44
4
47
53
59
59
5
3b
50b
60
60
6
48
3b
61
61
7
49
54
57a
57a
Третий тур 9.01.99
Лига / Задачи
Высшая
Первая
Вторая
Юниорская
1
62
74
75
75
2
64
75
77
77
3
65
63
78a
81
4
66
76
76
80a
5
67
77
81
83
6
68
78b
80b
73
7
69
79
82
84
Четвертый тур(финал) 10.01.99
Лига / Задачи
Высшая
Первая
Вторая
Юниорская
1
85c
85b
85a
85b
2
86
95
96
96
3
87b
92
100
90b
4
88
96
90a
95
5
89
97
99
99
6
90d
90c
101
103
7
91
87a
102
104
8
8
92
88
103
12
Примечание. Подчеркнутые задачи не были решены ни одним из участников.
2
Второй математический турнир старшеклассников “Кубок памяти А.Н. Колмогорова”
Санкт-Петербург, 4–10 января 1999 года
Задачи
1.
(А.С. Голованов) Среди 13 последовательных натуральных чисел 7 четных и 5 кратных трем. Сколько среди них чисел, кратных 6?
2.
(С.И. Токарев) Рыбаки ловили рыбу два дня. В первый день каждый рыбак поймал столько рыб,
сколько все остальные вместе во второй день. Докажите, что все рыбаки поймали за два дня поровну
рыб.
3.
(А.Я. Белов)
a) Существует ли непрерывная функция, график которой пересекается с любой прямой на плоскости?
b) f(x) – непрерывная монотонно возрастающая функция, определенная при всех действительных
x. Может ли ее график иметь ровно одну или две общие точки с каждой прямой?
4.
Дан параллелограмм ABCD. Проводятся три окружности: одна – с центром в точке B и радиусом BA,
вторая – с центром в точке D и радиусом DA, третья – описанная около треугольника BCD. Докажите, что существует точка, через которую проходят все три окружности.
5.
(А.В. Шаповалов) Может ли отношение двух чисел Фибоначчи быть равным 100?
6.
(Олимпиада США, 1998) Доска 19991999 раскрашена в шахматном порядке. За один ход разрешается перекрасить в противоположный цвет каждую клетку произвольного прямоугольника, образованного клетками доски. За какое наименьшее количество таких ходов можно сделать доску одноцветной?
7. (А.Я. Белов?) Период десятичной записи обыкновенной дроби имеет длину n. Каков наибольший
возможный период квадрата этой дроби?
8.
(Р. Садыков, М. Шаповалов) Два игрока по очереди проводят диагонали в правильном
1999-угольнике. После каждого своего хода игрок платит противнику число рублей равное количеству пересеченных диагоналей. Кто из игроков может получить больше денег независимо от игры
противника?
9.
(А.В. Шаповалов) В уравнении (...x2 -...x +...)(...x2 -...x +...)(...x2 -...x +...) = 0 вместо многоточий подставлены числа 3, 4, 5, 6, 7, 8, 9, 10, 11 в некотором порядке. Какое наибольшее число корней может
быть у этого уравнения?
10. (Д.Ю. Кузнецов) На шахматной доске расставлены n фишек так, что в любом квадрате 33 находятся
ровно 3 фишки.
a) При каком наибольшем n это возможно?
b) При каком наименьшем n это возможно?
11. Про числа a, b, c, d, известно, что a > c, b > d и a+b+c+d > 0. Докажите, что тогда |a+b|>|c+d|.
12. (Московские олимпиады) Известно, что a > b > 0 и
1  x y x y
x y
 . Докажите, что    
.
2  a b  ab
a b
13. (А.В. Пастор) В параллелограмме ABCD точка E – середина стороны BC, G – точка на стороне AB
такая, что DG перпендикулярно AB, а точка F, лежащая на стороне AD, такая, что EF=DE. Докажите,
что AGF=CED.
14. (А.С. Голованов) Прямоугольный треугольник вписан в параболу y = x2 . Докажите, что его гипотенуза не меньше 2.
15. (А.В. Шаповалов) В последовательности натуральных чисел каждый следующий член получается из
предыдущего прибавлением наибольшего делителя, являющегося точным квадратом (например, 24
 24+4). Известно, что никакой из членов не делится на 100. Докажите, что в этой последовательности лишь конечное число членов может делиться на 10.
16. (Неизвестный автор + Д.В. Карпов) В некотором государстве
n2  n  2
городов. Любые два го2
3
рода соединены либо проселочной, либо шоссейной дорогой. Докажите, что путешественник сможет, пользуясь дорогами только одного типа, посетить n городов, побывав в каждом из них ровно по
одному разу.
17. (А.В. Шаповалов)
a) Разрежьте правильный 36-угольник по непересекающимся диагоналям на равнобедренные треугольники.
b) Можно ли правильный многоугольник с 520 сторонами разбить непересекающимися диагоналями на равнобедренные треугольники?
18. BD – биссектриса в треугольнике ABC. На отрезке BD взята точка H такая, что угол DHC = 90о.
Докажите, что площадь треугольника ABH равна половине площади треугольника ABC.
19. (А.В. Шаповалов) Три одинаковые колоды карт положили друг на друга, предварительно каждую
перетасовав. Оказалось, что между дамами пик первой и второй колоды лежит столько же карт,
сколько между дамами пик второй и третьей колоды; то же верно для любых трех одинаковых карт
из всех трех колод. Докажите, что во всех трех колодах карты легли в одинаковом порядке.
20. (С.Г. Волченков) Блоха прыгает по плоскости, совершая прыжки одной и той же длины, но поворачивая каждый раз на 1 градус влево или вправо от предыдущего направления. Докажите, что она
может вернуться в исходную точку менее чем за 400 прыжков, если она отпрыгнула от этой точки на
40 прыжков.
21. (С.Л. Берлов) Натуральные числа a,b,c таковы, что ab делится на c, bc делится на a, а ca делится на b.
Докажите, что (a+b+c)a+b+c делится на abc.
22. (А.В. Шаповалов) Все члены двух различных непостоянных арифметических прогрессий
–натуральны. Числа первой прогрессии выписали подряд без пробелов, получив бесконечную последовательность цифр. То же сделали со второй прогрессией. Докажите, что получилась другая последовательность цифр.
23. (М. Гринчук, Московская олимпиада 1991) Между волейбольными командами двух стран был проведен матч-турнир, в котором каждая команда сыграла ровно по одному разу со всеми командами
другой страны. При этом каждая команда выиграла хотя бы одну встречу. Докажите, что найдутся
четыре команды A, B, C и D такие, что A выиграла у B, B выиграла у C, С выиграла у D, а D выиграла
у A. (Ничьих в волейболе не бывает)
24. (А.В. Шаповалов) В какое наименьшее число цветов можно раскрасить шахматную доску 100100
так, чтобы каждая клетка граничила по стороне с клеткой другого цвета, и между любыми двумя
клетками одного цвета ладья могла пройти по клеткам того же цвета (не перепрыгивая через другой
цвет)?
25. (А.И. Храбров) Пятизначное число с суммой цифр 37 делится на 37. Докажите, что его третья цифра
равна 9.
26. (А.Я. Белов, В.В. Произволов) Есть многочлен третьей степени P(x) = x3+ax2+bx+c. Известно, что если x – целое, то P(x) – куб целого числа. Докажите, что P(x)  (x+d)3 при некотором d.
27. (А.И. Галочкин) Всякий ли параллелепипед имеет в сечении прямоугольник?
28. (Л.А. Емельянов) Каждая грань куба со стороной 3 разбита на клетки 11. Поверхность куба удалось
оклеить семнадцатью бумажными полосками 31 и одним уголком так, что каждая полоска и уголок
закрыли по 3 целые клетки (возможно, с перегибанием через ребро). Найти все возможные расположения уголка.
29. (Л.А. Емельянов) На прямой отмечены два отрезка так, что ни один не содержится в другом. Найдите
геометрическое место точек, лежащих на плоскости вне прямой, из которых эти отрезки видны под
равными углами.
30. (А.В. Шаповалов) Двое играющих по очереди ломают палку: первый на две части, затем второй ломает любой из кусков на две части, затем первый – любой из кусков на две части, и т.д. Первый выигрывает, если сможет после какого-то из своих ходов сложить из 6 кусков два равных треугольника. Может ли второй ему помешать?
31. (М. Волчкевич) Решить уравнение (x2 + 100)2 + (x3 + 100)3 = 0.
32. (Московская олимпиада 1991) Докажите, что для любых положительных чисел a, b, c выполняется
4
неравенство
a
b

b
c

c
a

ab
ca

bc
ab

ca
bc
.
33. (С.И. Токарев) Имеется 6 одинаковых по виду гирек с массой 1,2,3,4,5,6 г. На гирьках сделали
надписи "1","2","3","4","5","6". Можно ли за два взвешивания на чашечных весах без гирь проверить, что надписи сделаны без ошибок?
34. (Бразильская олимпиада 1996, в переводе с сокращениями) Будем говорить, что несколько супружеских пар не образуют “устойчивого сообщества”, если среди них можно указать мужчину и женщину, которые не состоят в браке, но нравятся друг другу больше, чем их законные супруги. Пусть теперь есть 99 юношей и 99 девушек, где каждый из юношей составил список, в котором расположил
всех девушек в порядке убывания “предпочтений”, и где аналогичным образом поступили все девушки. Докажите, что руководствуясь этими списками, всегда возможно составить из них 99 супружеских пар, образующих “устойчивое сообщество”.
35. (М.Г. Сонкин) В четырехугольнике ABCD AB=AD и CB=CD, BAD=120o, BCD=60o. На стороне BC
выбрана точка M, а на стороне CD – точка N, так что MN касается окружности с центром в точке A
радиуса AB. Докажите, что диагональ BD делит площадь AMN в отношении 1:3.
36. (С.Л. Берлов) На плоскости дан равносторонний треугольник и точка внутри него. Эту точку несколько раз отражают относительно прямых, содержащих стороны треугольника, причем в конце
точка вновь оказывается внутри треугольника. Докажите, что она попадет на исходное место.
37. (С.Л. Берлов) По окружности расставлены натуральные числа, причем квадрат любого числа является делителем суммы квадратов соседей. Докажите, что все числа равны.
38. (С.Л. Берлов) В ABC проведена медиана AK. В AKB и AKC провели биссектрисы KL и KM. Докажите, что LM || BC.
39. (А.В. Шаповалов) Найдется ли 8 натуральных чисел таких, что никакое из них не делится ни на какое
другое, однако НОК любых двух из них равен одному и тому же числу?
40. (Р. Садыков) В кубике покрашено n ребер, но неизвестно какие. При каком наименьшем n можно
гарантировать, что найдется грань с четырьмя окрашенными ребрами?
41. (И.В. Изместьев) Пусть a, b и c – различные положительные числа такие, что a2, b2 и c2 – последо1
1
1
вательные члены арифметической прогрессии. Докажите, что числа
также обра,
,
bc ca ab
зуют арифметическую прогрессию.
42. (М.Г. Сонкин) Дан параллелограмм ABCD. Окружность с центром O, описанная вокруг ABD, вторично пересекает прямые BC и CD в точках E и F соответственно. Докажите, что луч AO делит угол
EAF пополам.
43. (С.Г. Волченков) Докажите, что для любого k существует степень пятерки, k последних цифр десятичной записи которой не содержат нулей.
44. (Жюри) На одной прямой расположены два компьютера и две розетки, к каждой из которых с помощью шнура длиной 1 м подключен один из компьютеров. Докажите, что, не перемещая компьютеры и не заменяя шнуры, можно подключить левый компьютер к левой розетке, а правый – к правой.
45. (И.Н. Сергеев) Даны числа a1  a2 … an и  >0. Набор чисел bi, (1  i  n), удовлетворяет неравенству |bi – ai| < . Пусть ci – такая перестановка чисел bi, что c1  c2  … cn. Докажите, что тогда |сi –
ai| <  для всех i.
46. (И.Н. Сергеев) Кронциркуль – это инструмент, похожий на циркуль, но на концах его две иголки. Он
позволяет только замерять расстояния между двумя произвольными точками и откладывать это расстояние на уже проведенной прямой (то есть по точке A на уже проведенной прямой можно найти
на этой же прямой точку B, лежащую от нее на замеренном расстоянии).
a) Как с помощью кронциркуля и линейки построить квадрат?
b) Даны две перпендикулярных прямых. Как с помощью только кронциркуля получить три вершины какого-то равностороннего треугольника?
5
c)
С помощью кронциркуля и линейки опустите перпендикуляр из данной точки на данную прямую.
47. (А.Я. Белов) Вдоль прямой записаны некоторые натуральные числа. Между соседними числами пишут их среднее арифметическое, а сами числа стирают. Верно ли, что после некоторого количества
таких операций либо появится нецелое число, либо все числа станут равными?
48. (С.Л. Берлов) Дан правильный многоугольник A1A2…An и точка O. Точки O1, O2,…,On – образы точки
O при симметрии относительно прямых (A1A2), (A2A3),…,(AnA1), точка H – центр многоугольника.
Докажите, что сумма векторов HO1+HO2+…+HOn равна нулю.
49. (А.В. Шаповалов) У прямоугольного параллелепипеда 11b окрасили одну грань 1b и положили
его на плоскость этой гранью вниз. Может ли он после 1999 перекатываний оказаться на том же месте, но окрашенной гранью вверх?
50. (С.Л. Берлов, Д.В. Карпов) Не более 10% жителей государства Х – враги народа. На день рождения
президента каждый гражданин государства сделал ему подарок: написал в ДГБ письмо со своей
подписью, разоблачающее одного из знакомых ему врагов народа. При этом известно, что честные
граждане разоблачали только истинных врагов, а враги могли как разоблачить других врагов, так и
оклеветать честных граждан.
a)
Известно, что у каждого гражданина этого государства менее 500 знакомых. Докажите, что на
основании полученных данных ДГБ может посадить некоторое количество граждан так, чтобы
больше половины посаженных была врагами народа.
b) Не читая этих доносов, президент приказал посадить всех граждан, на которых поступило не
менее, чем 1998 доносов. Верно ли, что более половины посаженных обязательно являются врагами народа?
51. (А.С. Голованов) Все натуральные числа раскрашены в розовый и голубой цвета так, что чисел каждого цвета бесконечно много. Докажите, что существует число, являющееся и суммой двух розовых,
и суммой двух голубых.
52. (С.Г. Волченков) На клетчатом поле nn двое по очереди делают ходы. Первый за один ход выставляет три фишки на любые свободные поля. Каждая фишка – черная или белая (по желанию первого
игрока). Второй за один ход переставляет одну из стоящих на поле фишек на любое свободное поле.
Если в какой-то момент образовались три фишки одного цвета, идущие подряд (по вертикали, горизонтали или диагонали), они снимаются с доски. Первый выигрывает, если все поля доски оказались
заняты. Второй выигрывает, если после его ходов какая-то позиция повторилась. Кто из игроков
может выиграть независимо от игры противника?
a) n=8;
b) n >3.
53. (А.И. Храбров) Семь дровосеков пилят пальмы при помощи двуручных пил. На одну пальму требуется два дровосека и час работы. За какое минимальное время они смогут спилить n пальм, если после каждого часа, работы им требуется часовой перерыв?
54. Дан параллелограмм ABCD. Вокруг треугольника ABС описана окружность. BE – диаметр этой
окружности. Докажите, что CDE= CBE или CDE+CBE=180.
55. (Д.А. Ростовский) Сережа занумеровал клетки шахматной доски числами от 1 до 64 (в произвольном порядке). Затем Дима перебрал всевозможные расстановки восьми не бьющих друг друга ладей
на этой доске и для каждой из этих расстановок посчитал сумму всех чисел под ладьями. После этого он выбрал наибольшую из посчитанных сумм. Какое наименьшее значение могла принимать эта
сумма.
56. (Israel-Hungary competition, 1994) Даны различные натуральные числа m и n. Докажите, что существует такое вещественное число х, что дробные части чисел mx и nx лежат на промежутке [1/3, 2/3].
57. (А.Я. Белов)
a) Даны числа a, b и с. Разрешается проводить следующие операции: возводить в куб, складывать,
вычитать, делить на 2, делить на 3. При этом можно использовать все промежуточные результаты. Как, используя только описанные операции, получить произведение abс?
b) Даны числа a, b, c и d. Разрешается проводить следующие операции: возводить в четвертую
степень, складывать, вычитать, делить на 2, делить на 3. При этом можно использовать все про-
6
межуточные результаты. Как, используя только описанные операции, получить произведение
abcd?
58. На доске написаны два числа 1998 и 1999. Каждую минуту два числа – a и b, записанные на доске,
ab
2
заменяются на числа
и
. Найдите произведение чисел на доске через 1999 минут.
1 1
2

a b
59. (М.Г. Сонкин) Дан параллелограмм ABCD. Вокруг треугольника ABС описана окружность. BE –
диаметр этой окружности. Докажите, что высоты треугольника ACD пересекаются в точке Е.
60. (А.Я. Белов + жюри) Докажите, что есть не меньше 1000 способов представить число 1998/1999 в
виде суммы нескольких чисел, обратных различным натуральным числам.
61. (И.Н. Сергеев, Московская олимпиада 1991) Для круглосуточной охраны объекта в течение месяца
нужно установить дежурство на посту в две смены: дневную и ночную. Дежурный может отработать
или дневную смену или ночную смену или сутки. После этого он должен отдыхать, соответственно,
не менее суток, полутора суток и двух с половиной суток. Какое наименьшее количество дежурных
потребуется для этого.
62. (С.Л. Берлов) Докажите, что для любых натуральных чисел a и b существует натуральное число n
такое, что an+bn+1 – составное число.
63. (А.В. Пастор) Дано 2000 точек. Рассматриваются всевозможные способы соединить их отрезками
трех цветов так, чтобы из каждой точки выходило ровно по одному отрезку каждого цвета, получившийся граф был связным и не имел кратных ребер. Докажите, что количество этих способов делится на четыре.
64. (А.В. Пастор) В графе 2000 вершин, степени всех вершин равны трем. Известно, что количество
способов раскрасить его ребра в три цвета так, чтобы из каждой вершины выходило ровно по одному ребру каждого цвета, не делится на четыре. Докажите, что в этом графе существует гамильтонов
цикл (т.е. цикл, проходящий через каждую вершину ровно один раз).
65. (А.В. Пастор) a, b, c > 0. Докажите неравенство:
2a 3 (a 3  1) 2
(b  c) 3

2b 3 (b 3  1) 2
( a  c) 3

2c 3 (c 3  1) 2
( a  b) 3
 3abc.
66. (А.С. Голованов) Существует ли такой выпуклый 1999-угольник, на сторонах которого (в порядке
обхода) лежат соответственно 1, 2, ..., 1999 точек с целыми координатами?
67. Числовая последовательность задана условиями: x1 = a, и xn+1 = (2xn-1)2 для n  1. Докажите, что в
любом интервале (, ) из отрезка [0, 1] найдется такое a, для которого все члены последовательности, начиная с некоторого, равны.
68. (А.Я. Белов) Какова наименьшая возможная длина последовательности букв русского алфавита, такой что никакая последовательность букв не повторяется два раза подряд, а при приписывании любой буквы справа это условие нарушается?
69. (А.Я. Белов) Кубическая решетка образована всевозможными плоскостями, параллельными координатным плоскостям и пересекающие оси координат в целых точках. Решетка рассечена плоскостью
ax+by+cz=0, где a, b и c - натуральные числа, взаимно простые в совокупности. Линии пересечения с
решеткой разбивают эту плоскость на многоугольники. Два таких многоугольника называются эквивалентными, если один получается из другого параллельным переносом. Докажите, что количество типов неэквивалентных многоугольников не превосходит a+b+c.
70. На сторонах BC, AC и AB треугольника ABC выбраны соответственно точки D, E и F, так, чтобы
DEF был подобен ABC. (A=D, E=B, F=C). Обозначим через H точку пересечения высот
FAE. Докажите, что длина отрезка HD не зависит от выбора точек D, E и F.
71. (И.С. Рубанов) Многочлены P(x,y) и Q(x,y) от двух переменных имеют целые коэффициенты. Известно, что при всех целых x и y значение P(x,y) делит значение Q(x,y). Докажите, что существует
многочлен R(x,y) такой, что Q(x,y) = R(x,y)P(x,y).
72. (С.Г. Волченков) Дано два единичных куба. Сначала Петя расставляет на ребрах обоих кубов стрелочки. Потом Вася совмещает эти кубы. Петя выигрывает, если после совмещения кубов больше
половины стрелочек одного куба совпадут с соответствующими стрелочками другого куба, а Вася –
7
если совпадут меньше половины стрелочек. Если совпадет ровно половина стрелочек, считается, что
игра закончилась вничью. Может ли кто-нибудь из них выигрывать независимо от игры противника,
и если да, то кто?
73. (С.Г. Волченков) Докажите, что на ребрах двух единичных кубов можно расставить стрелочки так,
что при любом совмещении этих кубов ровно на 6 ребрах обе проведенные стрелочки окажутся
одинаково направленными.
74. (Игорь Нагель) Дан прямоугольный треугольник ABC ( ACB = 90). На его катете AC как на диаметре построена окружность 1, а окружность 2 построена на катете BC как на диаметре. Окружность 3, касающаяся гипотенузы AB и окружности 1, проведена так, чтобы она в некоторой точке
K касалась продолжения катета BC за вершину B. Аналогично, окружность 4, касающаяся гипотенузы AB и окружности 2, проведена так, чтобы она в некоторой точке M касалась продолжения катета AC за вершину A. Докажите, что MC + KC = 2AB.
75. (А.В. Шаповалов) Есть веревочная сетка в виде квадрата 88, разбитого на ячейки 11. Какую самую
длинную веревку можно из нее вырезать? (От узлов можно отрезать любой конец не нарушая соединения остальных, но нельзя разрезать узел так, чтобы концов не образовалось).
76. (А.И. Храбров) Докажите неравенство: (a+2b+3c)22(a2+4b2+9c2)+8ab.
77. (А.И. Храбров) Два игрока по очереди делают ходы в следующей игре: первый ставит на шахматную
доску ладью, второй передвигает ее ходом коня, первый передвигает ее ходом слона, затем второй
снова – ходом коня и т.д. Ставить ладью на клетку, на которой она уже была, запрещено. Проигрывает не имеющий хода. Может ли кто-нибудь из игроков выигрывать независимо от игры противника, и если да, то кто?
78. (А.С. Голованов) Натуральные числа 1, 2, ..., 100 содержатся в объединении N геометрических прогрессий.
a) Докажите, что N  25.
b) Докажите, что N  31.
79. (А.Я. Белов) Докажите, что для любого многочлена P существует многочлен Q такой, что P(x) =
Q(x+1) – Q(x) при всех x.
80. (А.В. Шаповалов)
a) Параллелограмм разрезан на треугольники. Докажите, что хотя бы один из них можно накрыть
всеми остальными вместе.
b) Параллелограмм разрезан на выпуклые многоугольники. Докажите, что хотя бы один из них
можно накрыть всеми остальными вместе.
81. (Польская олимпиада, 1997) Решите в вещественных числах систему уравнений:
x+y2+z2= 3/8; x2+y+z2= 3/8; x2+y2+z= 3/8.
82. Несколько телефонов соединены проводами так, что каждый провод соединяет два телефона и каждая пара телефонов соединена не более чем одним проводом. Из каждого телефона ведет три провода. Верно ли, что провода всегда можно покрасить в три цвета так, что от каждого телефона отходили три провода разных цветов.
83. (М.Г. Сонкин) На сторонах AB и BC остроугольного треугольника ABC как на диаметрах во внешнюю сторону построены полуокружности S1 и S2 соответственно. Продолжения высот треугольника
ABC, опушенных из вершин C и A пересекаются с полуокружностями S1 и S2 в точках E и F соответственно. Докажите, что BE=BF.
84. (И.Ф. Шарыгин) Турист выехал из турбазы на байдарке в 10 ч. 15мин. с обязательством вернуться
обратно не позднее 13 ч. того же дня. Известно, что скорость реки 1,4 км/ч., а скорость байдарки 3
км/час. На какое максимальное расстояние турист сможет отъехать от турбазы, если через каждые 30
минут гребли он 15 минут отдыхает, не причаливая к берегу, а поворачивать он может только после
отдыха?
85. (С.Г. Волченков) У N ключей от N гостиничных номеров потерялись бирки. Известно, что каждый
ключ открывает ровно один из номеров. Какое наименьшее число пробных открываний дверей надо
сделать, чтобы наверняка определить, от какого номера каждый ключ?
a) N=4 ;
8
b) N=5 ;
c) N – произвольно.
86. (А.В. Шаповалов) В пространстве даны 6 точек, никакие 4 из которые не лежат на одной плоскости.
Докажите, что их можно разбить на две тройки так, что контуры двух треугольников с вершинами в
точках каждой из троек будут зацеплены.
87. (А.В. Шаповалов) Назовем лабиринтом шахматную доску 100100, где между некоторыми полями
вставлены перегородки, но так, что ладья может передвигаться по всей доске, не перепрыгивая через
перегородки. По команде ВПРАВО ладья смещается на одно поле вправо или, если справа край
доски или перегородка, остается на месте; аналогично выполняются команды ВЛЕВО, ВВЕРХ и
ВНИЗ. Конечную последовательность таких команд назовем программой.
a) Дан лабиринт. Докажите, что есть программа, выполнив которую, ладья окажется в верхней
правой клетке лабиринта независимо от того на какой клетке она стояла вначале.
b) Даны два лабиринта. Докажите, что есть программа, выполнив которую, ладья окажется в верхней правой клетке лабиринта независимо от того, в каком из двух лабиринтов и на какой клетке
она стояла вначале.
88. (К.А. Кноп) Дан остроугольный ABC и точка M внутри него. Длины сторон треугольника равняются
a, b и с. Докажите, что
MA 2
b2  c2  a2

MB 2
a2  c2  b2

MC 2
a2  b2  c2
1.
89. (А.С. Голованов) Существует ли строго убывающая последовательность x1, x2, …, xn положительных
чисел, удовлетворяющая при всех n > 1 условию xn  x n2  xn3 ?
90. (С.В. Конягин) Можно ли раскрасить натуральный ряд
a) в два цвета так, чтобы для любого натурального n числа n и 2n были окрашены в разные цвета?
b) в 3 цвета так, чтобы для любого натурального n числа n, 2n и 3n окрашены в разные цвета?
c) в 4 цвета так, чтобы для любого натурального n числа n, 2n, 3n и 4n были окрашены в разные
цвета?
d) в 6 цветов так, чтобы для любого натурального n числа n, 2n , …, 6n окрашены в разные цвета?
91. (С.Г. Волченков) Из двух разных прямоугольников один назовем меньшим, если его можно вырезать
из второго, причем его стороны будут параллельны сторонам второго прямоугольника, а площадь
меньше. Из некоторого прямоугольного листа бумаги вырезали несколько прямоугольников со сторонами, параллельными сторонам исходного прямоугольника. Затем каждый из вырезанных прямоугольников заменили на меньший. Всегда ли можно было для получения этого "уменьшенного"
набора обойтись меньшей заготовкой?
92. (П. Кожевников) В выпуклом пятиугольнике ABCDE на диагонали BD нашлась такая точка M, что
CBD=MEA, CDB=MAE . Докажите, что площади четырехугольника ABDE и треугольника
ACE равны.
93. (В.О. Бугаенко) Подряд без пробелов выписываются числа 1, 2,…, n. Существует ли такое n, что полученное число делится на 137?
94. (А. Храбров) Дан единичный круг и фиксировано число d<2. Двое играющих по очереди проводят в
этом круге отрезки без концов длины d, не имеющие общих точек с ранее проведенными отрезками.
Проигрывает тот, кто не может сделать хода. Может ли кто-нибудь из них выиграть независимо от
игры противника?
95. (С.И. Токарев?) За один ход разрешается отсечь от многоугольника треугольник прямой, не проходящей через вершины многоугольника. Вначале есть квадрат с точкой в центре. Докажите, что после
любого числа ходов точка не будет отсечена.
96. (А.В. Шаповалов) Матрос Фукс купил цифровые часы. Выяснилось, однако, что они настроены на
туземное 24-часовое время, которое отстает от московского на целое число минут, и перенастроить
их нельзя. Заметив, что все цифры, кроме 3,4,7, в перевернутом виде тоже выглядят как цифры, капитан Врунгель поставил часы вверх ногами (так что, например, вместо 05:21 видно 12:50). Оказалось, что теперь часы ровно 6 раз в сутки правильно показывают московское время. На сколько туземное время отстает от московского?
97. (В.И. Франк) f(x,y) – многочлен от двух переменных. Известно, что при любых натуральных a и b
9
число f(a,b) натурально и является общим делителем a и b. Докажите, что f(x,y)1.
98. (Д.Ю. Кузнецов) В каждой клетке таблицы nn записано по –1. Кроме того, фиксированы натуральные числа k и l, меньшие n. Разрешается одновременно поменять знаки у всех чисел, образующих
прямоугольник kl или прямоугольник lk. Докажите, что сделать все числа равными +1 возможно
только тогда, когда число n делится как на k, так и на l.
99. (С. Берлов) Во вписанном четырехугольнике ABCD точка K – середина стороны AD, а ABK=
DCK. Докажите, что AB=CD.
100.(А. Храбров) Треугольник обтянут по периметру леской, на которой отмечены краской точки, находящиеся в вершинах треугольника. Леску вращают вокруг треугольника. Докажите, что в некоторый
момент прямые, соединяющие вершины треугольника с соответствующими им точками на леске,
пересекутся в одной точке, и определите, при каком положении отмеченных точек это произойдет.
101.(А.В. Шаповалов) Посередине доски 1999 стоит столбик из 100 положенных друг на друга монет. За
один ход разрешается снять с верха любого столбика k монет (где k – любое число от 1 до всех) и
переставить их на k полей влево или вправо; если там уже стоит столбик, положить монеты на него.
Можно ли передвинуть столбик на соседнее справа поле менее чем за 15 ходов?
102.(А.И. Храбров) У квадратных трехчленов f и g коэффициенты при x2– ненулевые. Известно,
[f(x)]=[g(x)] при всех действительных x. Докажите, что f(x)=g(x) при всех действительных x.
103.(Задача из США) Пусть a и n – натуральные числа. Известно, что последняя цифра суммы
a+a2+...+an равна 1. Докажите, что последние цифры чисел a и n тоже равны 1.
104.(А.В. Шаповалов) Можно ли ребра куба раскрасить в два цвета так, чтобы можно было добраться от
любой вершины к любой другой как по ребрам одного цвета, так и по ребрам другого цвета?