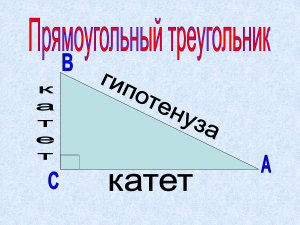
Прямоугольный треугольник Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть 90 градусов). Сторона, противоположная прямому углу, называется гипотенузой Стороны, прилегающие к прямому углу, называются катетами. Если длины всех трёх сторон прямоугольного треугольника являются натуральными числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую пифагорову тройку. Свойства прямоугольных треугольников 1. Сумма двух острых углов прямоугольного треугольника равна 90° 2. В прямоугольном треугольнике гипотенуза больше любого из катетов (является самой большой стороной). 3. Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°). 4. Площадь прямоугольного треугольника равна половине произведения двух его катетов. 5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла. 6. Теорема Пифагора: 𝑎2 + 𝑏2 = 𝑐 2 Признаки равенства прямоугольных треугольников 1. 2. 3. 4. 5. По двум катетам По катету и прилежащему острому углу По гипотенузе и острому углу По гипотенузе и катету По катету и противолежащему острому углу Признаки подобия прямоугольных треугольников 1. Если высота проведена к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. 2. Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу. 3. Высота есть среднее геометрическое (среднее пропорциональное) двух образованных ею сегментов гипотенузы, то есть ℎ 2=𝑎𝑐 ∗ 𝑏𝑐 4. Каждый катет треугольника есть среднее геометрическое гипотенузы и проекции катета на гипотенузу: 𝑏2=𝑐 ∗ 𝑏𝑐 𝑎 2 = 𝑐 ∗ 𝑎𝑐 5. В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов, то есть 𝑎𝑐 : 𝑏𝑐 = 𝑎 2: 𝑏2 6. Высота, опущенная на гипотенузу, связана с катетами прямоугольного треугольника соотношением: 1 1 1 𝑎𝑏 ℎ𝑐 = 2+ 2 = 2 𝑎 𝑏 ℎ𝑐 𝑐 1. По острому углу 2. По двум катетам 3. По катету и гипотенузе Центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы. 𝐶 R= 2 Радиус описанной около прямоугольного треугольника окружности равен длине медианы, проведенной к гипотенузе. Радиус вписанной в прямоугольный треугольник окружности определяется по формуле: Прямоугольный треугольник Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть 90 градусов). Сторона, противоположная прямому углу, называется гипотенузой Стороны, прилегающие к прямому углу, называются катетами. Если длины всех трёх сторон прямоугольного треугольника являются натуральными числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую пифагорову тройку. Свойства прямоугольных треугольников 1. Сумма двух острых углов прямоугольного треугольника равна 90° 2. В прямоугольном треугольнике гипотенуза больше любого из катетов (является самой большой стороной). 3. Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°). 4. Площадь прямоугольного треугольника равна половине произведения двух его катетов. 5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла. 6. Теорема Пифагора: 𝑎2 + 𝑏 2 = 𝑐 2 1. Если высота проведена к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. 2. Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу. 3. Высота есть среднее геометрическое (среднее пропорциональное) двух образованных ею сегментов гипотенузы, то есть ℎ2 =𝑎𝑐 ∗ 𝑏𝑐 4. Каждый катет треугольника есть среднее геометрическое гипотенузы и проекции катета на гипотенузу: 𝑏2 =𝑐 ∗ 𝑏𝑐 𝑎2 = 𝑐 ∗ 𝑎𝑐 5. В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов, то есть 𝑎𝑐 : 𝑏𝑐 = 𝑎2 : 𝑏2 6. Высота, опущенная на гипотенузу, связана с катетами прямоугольного треугольника соотношением: 1 1 1 𝑎𝑏 ℎ𝑐 = 2 + 2 = 2 𝑎 𝑏 ℎ𝑐 𝑐 Признаки подобия прямоугольных треугольников 1. По острому углу 2. По двум катетам 3. По катету и гипотенузе Признаки равенства прямоугольных треугольников 1. По двум катетам 2. По катету и прилежащему острому углу 3. По гипотенузе и острому углу 4. По гипотенузе и катету 5. По катету и противолежащему острому углу Центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы. 𝐶 R= 2 Радиус описанной около прямоугольного треугольника окружности равен длине медианы, проведенной к гипотенузе. Радиус вписанной в прямоугольный треугольник окружности определяется по формуле: Тригонометрия 𝛼 0⁰ 30⁰ 45⁰ 60⁰ 90⁰ 120⁰ 135⁰ 150⁰ 180⁰ 210⁰ 225⁰ 240⁰ 270⁰ 300⁰ 315⁰ 330⁰ 360⁰ 0 𝜋 6 sin 𝛼 0 1 2 cos 𝛼 1 tg 𝛼 0 ctg 𝛼 − функция sin 𝛼 cos 𝛼 tg 𝛼 , ctg 𝛼 В произвольном треугольнике стороны пропорциональны синусам противолежащих углов. 𝜋 3 𝜋 2 2 3 2 2 3 2 1 2 2 2 1 1 3 3 1 3 1 3 1 𝜋 4 0 − 0 2𝜋 3 3𝜋 4 5𝜋 6 𝜋 7𝜋 6 5𝜋 4 4𝜋 3 3𝜋 2 5𝜋 3 7𝜋 4 11𝜋 6 2𝜋 1 1 1 2 2 2 3 3 −1 3 0 0 − − − − − − 2 2 2 2 2 2 2 2 2 1 1 2 2 1 2 3 −1 3 3 0 1 − − − − − 2 2 2 2 2 2 2 2 2 1 1 1 − − 3 −1 − 0 1 0 − 3 −1 − 3 3 3 3 1 1 1 −1 − 3 − 1 0 − −1 − 3 − 3 − 3 3 3 𝛼 −𝛼 𝜋 −𝛼 2 𝜋 +𝛼 2 𝜋+𝛼 3𝜋 −𝛼 2 3𝜋 +𝛼 2 2𝜋 − 𝛼 2𝜋 + 𝛼 sin 𝛼 cos 𝛼 tg 𝛼 ctg 𝛼 − sin 𝛼 cos 𝛼 − tg 𝛼 − ctg 𝛼 cos 𝛼 sin 𝛼 ctg 𝛼 tg 𝛼 cos 𝛼 sin 𝛼 − sin 𝛼 − sin 𝛼 − cos 𝛼 − cos 𝛼 − ctg 𝛼 − tg 𝛼 tg 𝛼 − tg 𝛼 − cos 𝛼 ctg 𝛼 − cos 𝛼 − sin 𝛼 ctg 𝛼 tg 𝛼 − cos 𝛼 sin 𝛼 − ctg 𝛼 − tg 𝛼 − sin 𝛼 cos 𝛼 − tg 𝛼 − ctg 𝛼 sin 𝛼 cos 𝛼 tg 𝛼 ctg 𝛼 𝜋−𝛼