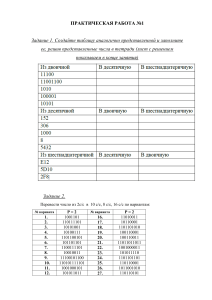
Практическая работа 4 Перевод чисел из одних систем счисления в другие Цель работы: научиться переводить числа из одних систем счисления в другие. Оборудование (приборы, материалы, дидактическое обеспечение): методические рекомендации к выполнению работы; задание и инструкционная карта для проведения практического занятия Компьютерные программы: Компьютерная программа калькулятор Содержание работы. Основные понятия. 1 Система счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков и правила действий с ними 2 Непозиционной называется такая система счисления, в которой значение каждого знака не зависит от его положения (места, позиции) в коде числа. 3 В позиционной системе счисления значение цифр зависит от позиции в числе. 4 К непозиционной системе счисления относится и римская, символы алфавита которой и обозначаемое ими количество представлены в таблице. Римские цифры I V X L С D М Значение (обозначаемое количество) 1 5 10 50 100 500 1000 5 Запись чисел в этой системе счисления осуществляется по следующим правилам: ‒ если цифра слева меньше, чем цифра справа, то левая цифра вычитается из правой; ‒ если цифра справа меньше или равна цифре слева, то эти цифры складываются. 6 В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен 7 Чтобы перевести число из некоторой системы счисления с основанием M ( цифрами 0, ..., M-1 ), иначе говоря, из M-ичной СС в десятичную, нужно представить его в виде: C = an * Mn + an-1 * Mn-1 + ... + a1 * M + a0.a1..n - цифры числа, из соответствующего диапазона. an первая цифра, a0 - последняя 8 Для того чтобы перевести число из десятичной системы в любую другую, необходимо это число делить на число – основание той системы, в которую переводится число. Остатки необходимо фиксировать и нумеровать. Число, полученное в результате деления – делим ещѐ раз, и так до тех пор, пока вновь полученное число уже само не станет остатком, т. е. будет меньше основания – оно замыкает цепочку остатков. Затем остатки, начиная с последнего, переписываем в число, которое является переведѐнным в другую систему счисления 9 В шестнадцатеричной СС, соответственно, шестнадцать цифр, но так как мы знаем всего десять, то вводятся дополнительные обозначения: A=10, B=11, C=12, D=13, E=14 и F=15. Задания 1 Выполнить действия и представить результат с помощью римских и арабских чисел 2 Определить системы счисления полученных чисел 3 Перевести эти числа в указанные в таблице системы счисления (расчеты представить в работе) 4 Провести перевод чисел с помощью ПК. 5 Результаты занести в таблицу: Исходное число Основание системы счисления 2 8 10 16 Задание 1 Исходные данные: 1 Выполнить действия и представить результат с помощью римских и арабских чисел: MCMXXVI + 264 – DXCII Решение: а) MCMXXVI = 1000 + 900 + 20 + 6 = 1926 б) DXCII = 500 + 90 + 2 = 592 в) 1926 + 264 – 592 = 1598 г) 1598 = MDXCVIII Задания 2-5 Исходные данные: Перевести числа 1698 и 13658 в указанные в задании системы счисления с помощью расчетов и с помощью калькулятора на ПК Решение: 1 В числе 1698 не указано основание системы счисления, значит это десятичная система счисления. В колонке 10 ставим прочерк. У числа 1365 индекс 8 указывает на восьмеричную систему счисления, прочерки в колонке 8. 2 Переведем число 1698 в двоичную, восьмеричную и шестнадцатеричную системы счисления: 1698 / 8 212(ост.2) 1698 / 2 849(ост.0) 1698 / 16 106(ост.2) 849 / 2 424(ост.1) 212 / 8 26(ост.4) 424 / 2 212(ост.0) 26 / 8 3(ост.2) 106 / 16 6(ост.10 А) 212 / 2 106(ост.0) 106 / 2 53(ост.0) 53 / 2 26(ост.1) 26 / 2 13(ост.0) 13 / 2 6(ост.1) 6 / 2 3(ост.0) 3 / 2 1(ост.1) А 13658 сначала переведем в десятичную систему счисления: 13658 = 1· 83 + 3· 82 + 6 · 8 + 5 = 512 + 192 + 48 + 5 = 757. А затем в двоичную и шестнадцатеричную: 757 / 2 378(ост.1) 757 / 16 47(ост.5) 378 / 2 189(ост.0) 47 / 16 2(ост.15 F ) 189 / 2 94(ост.1) 94 / 2 47(ост.0) 47 / 2 23(ост.1) 23 / 2 11(ост.1) 11 / 2 5(ост.1) 5 / 2 2(ост.1) 2 / 2 1(ост.0) После этого заносим в таблицу результаты вычислений в верхнюю строку заданного числа. 3 С помощью инженерного калькулятора (в Windows XP) или калькулятора программиста (в Windows 7) проверяем свои вычисления и вписываем результаты перевода чисел в нижнюю строку числа в таблице. 4 В итоге таблица должна выглядеть следующим образом: Исходное число Основание системы счисления 1698 10 13658 2 8 10 16 110101000102 32428 — 6А216 110101000102 32428 — 6А216 10111101012 — 757 2F516 10111101012 — 757 2F516 8 Порядок выполнения задания, методические указания: - ознакомиться с теоретическими положениями по данной теме; - изучить схему решения задач; - выполнить задания практической работы; - сформулировать вывод Содержание отчета: отчет по практической работе должен содержать: основные определения, рассуждения по решению задач, необходимые вычисления, ответ; вывод по работе Контрольные вопросы: 1 Что такое система счисления? 2 Какие бывают системы счисления? 3 Что такое непозиционная система счисления? 4 Что такое позиционная система счисления? 5 Какие знаки используются в римской системе счисления? 6 Каковы правила записи римских чисел? 7 Что такое позиционная CC? 8 Примеры позиционных систем счисления. 9 Как перевести число в десятичную СС? 10 Как перевести число в любую СС из десятичной? 11 Как обозначаются цифры в шестнадцатеричной СС? Литература: 1 О.В.Горбатова. Информатика, учебник для техникумов и колледжей ждт. – М.: ГОУ «УМЦ по образованию на ждт», 2008. 2 Н. Угринович Информатика и информационные технологии –М. Бином 2003г. 3 В.Ю. Микрюков Информация. Информатика. Компьютер. Информационные системы. Сети Ростов-на-Дону. Феникс. 2007 г. 4 http://algolist.manual.ru 5 http://kuzelenkov.narod.ru 6 http://ru.wikipedia.org