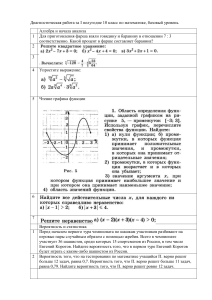
#
Вопросолампом
Ответ
Статус
1
Числовой матрицей размера m х n называется
прямоугольная таблица m х n
чисел, состоящая из m строк и n
столбцов
Верно
2
Квадратная матрица – это матрица, у которой …
число строк равно числу столбцов
Верно
- квадратная матрица
- нулевая матрица
3
Установите соответствие между матрицей и ее видом:
Верно
- единичная матрица
- нижняя треугольная матрица
4
Верно
#
Вопросолампом
Ответ
Статус
1)
2)
5
Верно
3)
4)
6
Математик Джеймс Сильвестр ввел термин «матрица» в …
1850 г.
Верно
Коммутативность - А + А = В + А
Ассоциативность - (А + В) + С = А +
(В + С)
7
Установите соответствие между свойствами сложения матриц А и В и их записями:
Верно
Сложение с нейтральным
элементом - А + 0 = 0 + А
Сложение с противоположным
элементом - А + (-а) = (-а) + А + 0
#
Вопросолампом
8
Неверно, что матрицы в паре … можно перемножить (укажите 2 варианта ответа)
9
Неверно, что произведение матриц А и В вводится только в том случае, когда …
Ответ
Статус
Не
верно
матрицы А и В одной
размерности
Не
верно
#
Вопросолампом
10
Ответ
Статус
Строки и столбцы поменяли
местами с сохранением порядка.
Верно
Каким образом была получена матрица АT?
#
Вопрос
Ответ
Статус
1
Не
верно
2
Верно
3
Разностью матриц А и В называется … матрицы А с матрицей, противоположной матрице
В
сложение
Не
верно
#
Вопрос
Ответ
Статус
4
Дистрибутивность (*) умножения справа относительно сложения матриц выглядит так: …
C*(A+B)=C*A+C*B
Не
верно
5
Числовой множитель можно … за знак транспонирования
выносить
Верно
6
Минор элемента матрицы совпадает с алгебраическим дополнением в случае, когда …
(i + j) – четное
число
Верно
7
Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель
равен …
нулю
Верно
8
Ранг матрицы при элементарных преобразованиях …
не меняется
Верно
9
-176
Верно
10
-441
Верно
#
Вопрос
Ответ
Статус
Ранг основной
матрицы - 2
Ранг расширенной
матрицы - 3
11
Верно
Количество
решений системы
-0
1) составить
расширенную
матрицу системы
12
Расположите в правильном порядке шаги решения системы уравнений методом Гаусса:
2) с помощью
элементарных
преобразований
привести
расширенную
матрицу системы
к ступенчатому
виду
Верно
#
Вопрос
Ответ
Статус
3) на основе
полученной
ступенчатой
матрицы
составить и
решить систему
линейных
уравнений
13
142
Верно
14
-49
Верно
15
Верно
#
Вопрос
Ответ
Статус
16
Система линейных уравнений называется … системой линейных уравнений, если все
свободные члены в этой системе равны нулю
однородной
Верно
Нуль-вектор вектор, начало и
конец которого
совпадают
17
Установите соответствие между понятием и его определением:
Коллинеарные
векторы векторы, лежащие
на одной прямой
или на
параллельных
прямых
Верно
Длина вектора длина
соответствующего
отрезка
18
Расположите записи векторных операций в порядке «скалярное произведение векторов,
векторное произведение векторов, смешанное произведение векторов»:
1)
Верно
#
Вопрос
Ответ
Статус
2)
3)
19
√201
Верно
20
-49
Верно
неколлинеарных
Верно
22
√992
Верно
23
{-5,10,-5}
Верно
24
27
Верно
21
Всякий вектор на плоскости можно выразить в виде линейной комбинации любых двух
… векторов
#
Вопрос
Ответ
Статус
1)
2)
3)
25
Расположите прямые y1, y2 и y3, заданные уравнениями, в порядке возрастания их
угловых коэффициентов:
Верно
1) y2=5
2) y1=7x-2
3) y3=-x+3
26
Уравнение прямой, проходящей через точки A(-2,-3) и B(-7,-5), имеет вид …
27
28
Каноническое уравнение прямой, проходящей через точки A(-3,2) и B(7,-8), имеет вид …
y=0,4x-2,2
Верно
параллельны
Не
верно
Верно
#
Вопрос
Ответ
Статус
29
Косинус угла между прямыми y1=-2x+5 и y2=2x-2 равен …
0,6
Верно
30
Уравнение … является параметрическим уравнением прямой
31
Ордината точки пересечения прямых y1=2x+1 и y2=-2x+3 равна …
Верно
2
Верно
-
32
Установите соответствие между способом задания плоскости в пространстве и ее
уравнением:
-
Верно
-
33
Уравнение плоскости, проходящей через точки A(-2,2,8), B(4,0,6) и C(2,0,6), имеет вид …
y-z+6=0
34
35
Верно
-
Расположите обозначения взаимного расположения прямой l и плоскости α в порядке
«прямая пересекает плоскость, прямая перпендикулярна плоскости, прямая
параллельна плоскости»:
1) l∩α
Верно
#
Вопрос
Ответ
Статус
2) l ⊥ α
3) l ∥ α
36
Прямая, проходящая через основания перпендикуляра и наклонной, называется …
проекцией
Верно
37
Сумма координат нормального вектора плоскости 2x-y+3z-2=0 равна …
2
Не
верно
38
Разность координат нормального вектора плоскости 2x-y+3z-2=0 равна …
4
Не
верно
39
Сумма координат середины отрезка с концами в точках A(-3,-2,5) и A(5,2,1) равна …
4
Верно
40
Матрица, дважды транспонированная, равна …
исходной матрице
Верно
#
Вопрос
1
Ответ
Статус
определителем
Верно
2
Понятие определителя вводится для … матриц
квадратных
Верно
3
Определитель квадратной матрицы равен … произведений элементов любой строки
(столбца) на их алгебраические дополнения
сумме
Верно
A(1×1) - a11
4
Установите соответствие между размерностью матрицы и формулой для вычисления ее
определителя:
A(2×2) - a11a22a12a21
Верно
A(3×3) -
5
-22
Верно
#
Вопрос
Ответ
Статус
1) M13
2) M21
6
Верно
3) M11
4) M32
7
88
Верно
8
3
Не
верно
#
Ответ
Статус
9
-88
Не
верно
10
Определитель
матрицы был
найден при
помощи
теоремы
Лапласа.
Не
верно
Ответ
Статус
#
Вопрос
Вопрос
1)
2)
1
Верно
3)
#
Вопрос
Ответ
Статус
4)
2
(2,1,1)
Верно
3
Совместная
система
уравнений система
уравнений,
имеющая хотя
бы одно
решение
Верно
Установите соответствие понятия и его характеристики
Несовместная
система
уравнений система
уравнений, не
#
Вопрос
Ответ
Статус
имеющая
решений
Определенная
система
уравнений совместная
система
уравнений,
имеющая
единственное
решение
4
имеет
бесконечно
много решений
Верно
5
7
Не
верно
#
Вопрос
Ответ
Статус
6
-
7
-
8
(4,0,-1)
Верно
#
9
Вопрос
Ответ
Статус
Найти
определитель
матрицы;
найти значения
n
определителей
путем замены
первого
столбца
коэффициентов
столбцом из
свободных
членов; найти
значение
неизвестных
через
отношения
советующих
полученных
определителей
к
определителю
изначальной
матрицы.
Верно
#
Вопрос
Ответ
10
#
Статус
-
Вопрос
Ответ
Статус
Векторы направленные
отрезки
1
Установите соответствие между понятием и его определением:
Единичные
векторы векторы, длина
которых равна
единице
Компланарные
векторы -
Верно
#
Вопрос
Ответ
Статус
векторы,
лежащие в
одной
плоскости или в
параллельных
плоскостях
1)
2
2)
Верно
3)
3
Верно
4
-20
Верно
5
тривиальной
Не
верно
#
Вопрос
Ответ
Статус
6
Два вектора образуют базис на плоскости тогда и только тогда, когда эти векторы …
неколлинеарны
Верно
7
4
Верно
8
{-3,-6,-3}
Не
верно
9
-
10
Не
верно
#
Вопрос
Ответ
Статус
Общее уравнение
прямой 1
Установите соответствие
между способом задания
прямой на плоскости и
уравнением прямой:
-
Верно
-
1) y2=x+2
2
Расположите прямые y1, y2 и
y3, заданные уравнениями, в
порядке убывания их угловых
коэффициентов:
2) y1=-x-3
Верно
3) y3=-3x
3
Уравнение прямой,
проходящей через точки
A(2,3) и B(0,5), имеет вид …
4
Говоря о взаимном
расположении двух прямых
y1=3x+5 и y2=-2x+1 на
y=-x+5
Верно
-
#
Вопрос
Ответ
Статус
плоскости, можно
утверждать, что эти прямые …
5
Каноническое уравнение
прямой, проходящей через
точки A(2,3) и B(0,5), имеет
вид …
6
Расстояние от точки A(1,5) до
прямой 3x-4y-3=0 равно …
4
Верно
7
Угол между прямыми x3y+5=0 и 2x+4y-7=0 равен …
45°
Верно
8
Уравнение … является
уравнением прямой с
угловым коэффициентом
Не
верно
9
Ордината точки пересечения
прямых y1=2x+1 и y2=-2x-1
равна …
Верно
10
Дана прямая 5x + 5y – 7 = 0.
Какой угол образует с
Верно
135
Верно
#
Вопрос
Ответ
Статус
положительным
направлением оси абсцисс
данная прямая?
#
Вопрос
Ответ
Статус
-
1
Установите соответствие между способом задания плоскости в пространстве и ее
уравнением:
-
Верно
-
2
-
1) Al+Bm+Cn=0
3
Верно
2)
#
Вопрос
Ответ
Статус
3)
4
Плоскости в пространстве называются параллельными, если они …
5
Расстояние от точки A(3,9,1) до плоскости 2x-y+3z=2 равно …
6
Сумма координат нормального вектора плоскости 3x-y+2z+1=0 равна …
7
Разность координат нормального вектора плоскости 3x-2y+z-1=0 равна …
8
Координаты середины отрезка с концами в точках A(3,2,5) и В(5,2,7) равны …
(4,2,6)
Верно
9
Сумма координат середины отрезка с концами в точках A(3,2,5) и В(5,2,7) равна …
12
Верно
10
Медиана – это прямая, проходящая из вершины A к середине стороны BC. Нужно найти
координаты точки M- середины стороны BC. Запишите уравнение прямой, проходящей
через две заданные точки A и M.
#ВопросОтветСтатус1
не имеют общих точек
Верно
Не
верно
5
Не
верно
-
Не
верно
Сложение матрицы с матрицей.
Верно2
Определитель равен 24, будет совпадать.
Не верно3
Записать расширенную матрицу системы; выполнить алгебраические преобразования; получить эквивалентную систему уравнений; вычислить значение
свободных неизвестных.
Не верно4
Не верно5
Известно, что прямая проходит через точки A(1; 1) и B(–2; 3). Найти угловой коэффициент k данной прямой и ординату b точки ее пересечения с осью Oy.
k = –2/6; b = –5/6.Не верно6
Прямые 15x + 36y –105 = 0 и 5x + 12y + 30 = 0 параллельны.
Найдите расстояние между данными прямыми.
Расстояние между данными прямыми равно 9.
Не верно7
Верно8
x ∈ [0; 4].
Верно9
-6x2 siny.
Не верно10
Дано дифференциальное уравнение: y'+2y=4x.Решите это уравнение.
2x-1+C⋅e-2x.
Верно
РЕЗУЛЬТАТ ПОПЫТКИ ТЕСТА
#
Вопрос
Ответ
Статус
1
Сложение матрицы с матрицей.
Верно
2
Определитель равен 24, совпадать не
будет.
Не
верно
3
Не
верно
4
Верно
#
Вопрос
Ответ
5
Верно
6
7
Дана функция f(x) = lg(3x − 1) + 2lg(x + 1).Найдите область определения функции.
8
9
Статус
Дана функция: z=x2-2xy2+y3. Найдите частные производные второго порядка для этой
функции.
x ∈ [0; 4).
Не
верно
x ∈ (3; +∞).
Не
верно
y^'=0,7t5.
Верно
-4x+8y.
Не
верно
Дано линейное дифференциальное уравнение второго порядка: y''-4y'+5y=0.
10
Верно
Решите это уравнение.
РЕЗУЛЬТАТ ПОПЫТКИ ТЕСТА
#
Вопрос
1
Ответ
Статус
Определитель равен 12,
совпадать не будет.
Не
верно
2
3
Верно
Известно, что прямая проходит через точки A(1; 1) и B(–2; 3). Найти угловой
коэффициент k данной прямой и ординату b точки ее пересечения с осью Oy.
Прямые 15x + 36y –105 = 0 и 5x + 12y + 30 = 0 параллельны.
4
Найдите расстояние между данными прямыми.
5
k = –2/3; b = –5/3.
Верно
Расстояние между
данными прямыми равно
5.
Верно
x ∈ [0; 4].
Верно
#
Вопрос
Ответ
Статус
6
Дана функция f(x) = lg(3x − 1) + 2lg(x + 1).Найдите область определения функции.
x ∈ ( 1/3; +∞).
Верно
Дана функция, заданная неявно: 2x2 + 3y2 = 9x.
Не
верно
7
Найдите производную данной функции
8
9
Дано дифференциальное уравнение: y'+2y=4x.Решите это уравнение.
10
Дано линейное дифференциальное уравнение второго порядка: y''-4y'+5y=0.
-3x2 siny.
Не
верно
2x-1+C⋅e-2x.
Верно
Не
верно
Решите это уравнение
Результат попытки теста
# Вопрос
Ответ
Статус
1 Габриэль Крамер опубликовал «правило Крамера» в …
1751 г.
Верно
# Вопрос
Ответ
Статус
2
Не
верно
3 Матрица А называется матрицей, … с матрицей В, если число столбцов матрицы А равно числу строк матрицы В согласованной
Верно
4 Какое из следующих действий не относится к элементарным преобразованиям матрицы
возведение строки в
квадрат
Верно
A∙X=B - X=A-1∙B
5 Сопоставьте матричные уравнения и их решения
X∙A=B - X=B∙A-1
Верно
A∙X∙C=B - X=A-1∙B∙C-1
6
-10
Не
верно
7
-193
Верно
8
-
9 Три вектора образуют базис в пространстве тогда и только тогда, когда эти векторы …
не компланарны
Верно
10
{-6,12,-6}
Верно
# Вопрос
Ответ
Статус
11
33
Верно
Прямые параллельны k1=k2,b1≠b2
12
Установите соответствие между взаимным расположением прямых y1=k1 x+b1 и y2=k2 x+b2 на плоскости и
условием этого расположения:
Прямые перпендикулярны
Верно
- k1∙k2=-1
Прямые совпадают k1=k2,b1=b2
1) y3=-9
13 Расположите прямые y1, y2 и y3, заданные уравнениями, в порядке убывания их угловых коэффициентов:
2) y1=-7x+1
Верно
3) y2=-8x+2
14 Две прямые y1=7x+5 и y2=7x-5 на плоскости …
параллельны
Верно
15 Расстояние от точки A(2,1) до прямой 3x-4y-3=0 равно …
Не
верно
16 Косинус угла между прямыми y1=2x+1 и y2=-x+2 равен …
Верно
# Вопрос
Ответ
17 Разность координат нормального вектора плоскости 3x-y+2z+2=0 равна …
Статус
-
18 Координаты середины отрезка с концами в точках A(3,-2,5) и A(5,2,-7) равны …
(4,-2,6)
Не
верно
19 Пусть даны множества A={3,4,5} и B={7,6,5}, тогда сумма всех элементов множества A∪B равна …
25
Не
верно
20
-2
Не
верно
Приращение функции в
точке x0 -
21 Установите соответствие между понятием и соответствующей формулой:
Дифференциал функции -
Верно
Производная функции в
точке x0 22
Верно
23
экстремумом
Не
верно
24 Расположите значения данных интегралов в порядке убывания:
1)
Верно
# Вопрос
Ответ
Статус
2)
3)
25
2√3
Не
верно
26
sin(x+2)+C
Не
верно
z=3x2+5x-2y - zx' =6x+5
27 Установите соответствие между функцией двух переменных и ее частной производной по переменной x:
z=x2-x+1 - zx' =2x-1
Верно
z=2x3-3x - zx' =6x-3
28 Значение функции z(x;y)=3x-2y+16 в точке A(1; 2) равно …
15
Верно
29 Дифференциал функции двух переменных z=3x+2y имеет вид …
dz=3dx+2dy
Верно
30 Функция k=3x+5y-2z+1 является функцией …
трех переменных
Верно
#
1
Вопрос
Ответ Статус
Дан матричный многочлен f(A) = 3A2– 5A + 2. Нужно вычислить его значение.
Приведите метод решения.
Найти значение A2, умножить на 3, умножить матрицу А на -5, сложить полученные матрицы, прибавить к ней матрицу с элементами главной диагонали,
равной 2.
Верно
2
Существует, таr как ее определитель отличен от нуля.
Верно
3
Записать расширенную матрицу системы; выполнить элементарные преобразования; получить эквивалентную систему уравнений; совершить обратный
ход Гаусса, вычислив значения неизвестных.
Верно
4
Известно, что прямая проходит через точки A(1; 1) и B(–2; 3). Найти угловой коэффициент k данной прямой и ординату b точки ее пересечения с осью Oy.
k = –2/3; b = –5/3.
Верно
5
Прямые 15x + 36y –105 = 0 и 5x + 12y + 30 = 0 параллельны.
Найдите расстояние между данными прямыми.
Расстояние между данными прямыми равно 5.
Верно
6
Верно
7
Дана функция, заданная неявно: 2x2 + 3y2 = 9x.
Найдите производную данной функции
Верно
8
y^'=0,7t5.
Верно
9
Фигура, образованная путем вращения вокруг оси Oх, ограничена линиями y=4x-x2,y=x. Найдите объем данного тела.
Не верно
10
-x2 siny.
Верно
РЕЗУЛЬТАТ ПОПЫТКИ ТЕСТА
#
Вопрос
Ответ
Статус
1
Сложение
матрицы с
матрицей
Верно
2
Найти
значение A2,
умножить на 3,
умножить
матрицу А на 5, сложить
полученные
матрицы,
прибавить к
ней матрицу с
элементами
главной
Верно
Дан матричный многочлен ⨍ (A) = 3A2 – 5A +2. Нужно вычислить его значение.
Приведите метод решения.
#
Вопрос
Ответ
Статус
диагонали
равной 2.
3
Существует, та
как ее
определитель
отличен от
нуля.
Верно
4
При помощи
формулы
треугольника.
Верно
Система имеет
бесконечное
число
решений, так
как система
несовместна.
Не
верно
Как был найден определитель матрицы?
5
#
Вопрос
6
4
Числовой множитель можно … за знак транспонирования
Ответ
Статус
Найти
определитель
матрицы;
найти значения
n
определителей
путем замены
первого
столбца
коэффициентов
столбцом из
свободных
членов; найти
значение
неизвестных
через
отношения
советующих
полученных
определителей
к
определителю
изначальной
матрицы.
Верно
выносить Верно
5
Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен …
нулю Верно
6
Если элементы двух строк (столбцов) матрицы …, то определитель равен нулю
пропорциональны Верно
7
Матрица А называется …, если ее определитель отличен от нуля
невырожденной Верно
8
Базисным минором матрицы называется всякий отличный от нуля минор, порядок которого равен … матрицы
рангу Верно
9
Ранг основной матрицы - 2
Ранг расширенной матрицы - 3
Количество решений системы - 0 Верно
10
142
Верно
11
-49
Верно
12
-116
Верно
13
Верно
14
Матрица называется … матрицей, если в каждой ее ненулевой строке имеется такой ненулевой элемент, что все остальные элементы столбца,
содержащего этот элемент, равны нулю
ступенчатой Не верно
15
Расположите записи векторных операций в порядке «скалярное произведение векторов, векторное произведение векторов, смешанное произведение
векторов»:
1)
2)
3) Верно
16
24
Верно
17
√992
Верно
18
Расположите прямые y1, y2 и y3, заданные уравнениями, в порядке возрастания их угловых коэффициентов:
1)
2)
3)
1) y3=-x+3
2) y2=5
3) y1=7x-2 Не верно
19
Уравнение прямой, проходящей через точки A(-2,-3) и B(-7,-5), имеет вид …
y=0,4x-2,2
Верно
20
21
Сумма координат точки пересечения прямых y1=3x+2 и y2=-2x+3 равна …
2.8 Верно
22
Установите соответствие между способом задания плоскости в пространстве и ее уравнением:
- Верно
23
Уравнение плоскости, проходящей через точки A(-2,2,8), B(4,0,6) и C(2,0,6), имеет вид …
y-z+6=0 Верно
24
2 Верно
25
Прямая, проходящая через основания перпендикуляра и наклонной, называется …
проекцией Верно
26
Расстояние от точки A(2,4,1) до плоскости 2x-y+3z=2 равно …
Верно
27
Сумма координат нормального вектора плоскости 2x-y+3z-2=0 равна …
4 Верно
28
Разность координат нормального вектора плоскости 2x-y+3z-2=0 равна …
Верно
29
Сумма координат середины отрезка с концами в точках A(-3,-2,5) и A(5,2,1) равна …
4 Верно
30
Матрица, дважды транспонированная, равна …
исходной матрице
Верно
13 Feb 2024 at 11:51 pm
Like
- Reply
Viktoria Andreychuk
1
A+B A-B A⋅B B⋅A - Верно
2
В древнем Китае матрицы называли …
«волшебными квадратами» Верно
3
Расположите матрицы в порядке «нижняя треугольная, квадратная, верхняя треугольная, неквадратная»:
1)
2)
3)
4) Верно
4
Сопоставьте матричные уравнения и их решения
A∙X=B - X=A-1∙B
X∙A=B - X=B∙A-1
A∙X∙C=B - X=A-1∙B∙C-1 Верно
5
Число, равное наивысшему порядку минора матрицы, называется … матрицы
рангом Верно
6
При перестановке двух строк матрицы ее определитель …
меняет знак на противоположный Верно
7
Матрица А называется невырожденной, если …
|A|≠0 Верно
8
17
Верно
9
34
Верно
10
Верно
11
1 Верно
12
1)
2)
3) Верно
13
-34 Верно
14
координатами Верно
15
{-6,12,-6}
Верно
16
Установите соответствие между взаимным расположением прямых y1=k1 x+b1 и y2=k2 x+b2 на плоскости и условием этого расположения:
Прямые параллельны - k1=k2,b1≠b2
Прямые перпендикулярны - k1∙k2=-1
Прямые совпадают - k1=k2,b1=b2 Верно
17
Уравнение плоскости, проходящей через точки A(1,2,3), B(4,5,6) и C(2,4,6) имеет вид …
x-2y+z=0 Верно
18
Не верно
19
Точка x0 называется точкой минимума функции y=f(x), если для всех точек x≠x0 из некоторой окрестности точки x0 выполняется …
неравенство f(x)<f(x0)
Не верно
20
Значение производной функции y=ln(1+5x) в точке x0=0 равно …
Не верно
21
Верно
22
Верно
23
3
Не верно
24
Функция k=3x+5y-2z+1 является функцией …
четырех переменных Не верно
25
Данное дифференциальное уравнения (2x+1) y'+y=x …
является линейным
Верно
26
Установите соответствие между правой частью нелинейного однородного дифференциального уравнения второго порядка с постоянными
коэффициентами и его частным решением
f(x)=aemx,m≠k1≠k2 f(x)=aemx,m=k1 f(x)=ax2+bx+c - Верно
27
Общее решение уравнения y''+5y'-6y=0 имеет вид …
y=c1e6x+c2e3x
Не верно
28
Функции y1=y1(x) и y2=y2(x) называются линейно … на (a,b), если равенство α1 y1+α2 y2+0 выполняется тогда и только тогда, когда хотя бы одно из чисел
α1 или α2 отлично от нуля
независимыми Верно
29
Если дифференцируемые функции y1=y1(x) и y2=y2 (x) линейно независимы от решения дифференциального уравнения на (a,b), то определитель
Вронского на этом интервале нигде не может быть равен …
0
Верно
30
Условием существования двух действительных корней характеристического уравнения дифференциального уравнения является то, что дискриминант
характеристического уравнения …
больше нуля Верно
РЕЗУЛЬТАТ ПОПЫТКИ ТЕСТА
#
Вопрос
Ответ
Статус
1)
2)
1
Верно
3)
4)
2
Не
верно
#
Вопрос
Ответ
3
Статус
Верно
4
Разностью матриц А и В называется … матрицы А с матрицей, противоположной матрице
В
Сумма
Верно
5
Дистрибутивность (*) умножения справа относительно сложения матриц выглядит так: …
C*(A-B)=C*A-C*B
Не
верно
6
Числовой множитель можно … за знак транспонирования
выносить
Верно
7
Минор элемента матрицы совпадает с алгебраическим дополнением в случае, когда …
(i + j) – четное
число
Верно
8
Если элементы двух строк (столбцов) матрицы …, то определитель равен нулю
Пропорциональны
Верно
9
Матрица А называется …, если ее определитель отличен от нуля
невырожденной
Верно
10
Ранг матрицы при элементарных преобразованиях …
не меняется
Верно
#
Вопрос
11
Ответ
Статус
-176
Верно
12
-
1)
2)
3)
13
Расположите в правильном порядке шаги решения системы уравнений методом Гаусса:
Верно
4)
1) составить
расширенную
матрицу системы
#
Вопрос
Ответ
Статус
2) с помощью
элементарных
преобразований
привести
расширенную
матрицу системы к
ступенчатому виду
3) на основе
полученной
ступенчатой
матрицы составить
и решить систему
линейных
уравнений
14
142
Верно
15
-116
Верно
#
Вопрос
Ответ
Не
верно
16
17
Статус
Матрица называется … матрицей, если в каждой ее ненулевой строке имеется такой
ненулевой элемент, что все остальные элементы столбца, содержащего этот элемент,
равны нулю
18
Нулевой
Не
верно
5
Не
верно
Нуль-вектор вектор, начало и
конец которого
совпадают
19
Установите соответствие между понятием и его определением:
Верно
Коллинеарные
векторы - векторы,
лежащие на одной
#
Вопрос
Ответ
Статус
прямой или на
параллельных
прямых
Длина вектора длина
соответствующего
отрезка
1)
20
Расположите записи векторных операций в порядке «скалярное произведение векторов,
векторное произведение векторов, смешанное произведение векторов»:
2)
Верно
3)
21
22
Всякий вектор на плоскости можно выразить в виде линейной комбинации любых двух
… векторов
√201
Верно
Неколлинеарных
Верно
#
Вопрос
Ответ
Статус
23
24
Верно
24
√992
Верно
25
-
26
33
Не
верно
Известны точка
M(x0,y0) и угловой
коэффициент k -
27
Установите соответствие между способом задания прямой на плоскости и уравнением
прямой:
Известны точки
A(x1,y1) и B(x2,y2) -
Верно
Известны отрезки
aиb-
28
Уравнение прямой, проходящей через точки A(-2,-3) и B(-7,-5), имеет вид …
y=0,4x-2,2
Верно
#
Вопрос
Ответ
Статус
29
Сумма координат точки пересечения прямых y1=3x+2 и y2=-2x+3 равна …
2,8
Верно
30
Каноническое уравнение прямой, проходящей через точки A(-3,2) и B(7,-8), имеет вид …
31
Верно
3
Не
верно
32
Косинус угла между прямыми y1=-2x+5 и y2=2x-2 равен …
0,6
Верно
33
Уравнение плоскости, проходящей через точки A(-2,2,8), B(4,0,6) и C(2,0,6), имеет вид …
y-z+6=0
Верно
34
-
1) l∩α
35
Расположите обозначения взаимного расположения прямой l и плоскости α в порядке
«прямая пересекает плоскость, прямая перпендикулярна плоскости, прямая
параллельна плоскости»:
2) l ⊥ α
3) l ∥ α
Верно
#
Вопрос
Ответ
Статус
36
Расстояние от точки A(2,4,1) до плоскости 2x-y+3z=2 равно …
37
Сумма координат нормального вектора плоскости 2x-y+3z-2=0 равна …
38
Разность координат нормального вектора плоскости 2x-y+3z-2=0 равна …
39
Сумма координат середины отрезка с концами в точках A(-3,-2,5) и A(5,2,1) равна …
4
Верно
40
Матрица, дважды транспонированная, равна …
исходной матрице
Верно
Верно
4
Верно
-
РЕЗУЛЬТАТ ПОПЫТКИ ТЕСТА
#
Вопрос
1
Найдите область определения функции
Ответ
Статус
2
Не
верно
#
Вопрос
2
Ответ
Статус
1
Верно
2
Не
верно
не существует
Не
верно
0
Не
верно
Укажите область определения функции
3
Найдите предел
4
Найдите
5
Найдите предел
#
Вопрос
6
Ответ
Статус
3
Не
верно
2
Не
верно
4
Верно
1
Верно
xe^x
Верно
Найдите предел
7
Найдите предел
8
Вычислите предел по правилу Лопиталя
9
Вычислите предел по правилу Лопиталя
10
Найдите производную функции y = xe^x - e^x
#
Вопрос
11
Ответ
Статус
3
Не
верно
убывает
Верно
3
Не
верно
прямая l, если
расстояние от
переменной
точки М
Верно
Найдите производную функции
12
Определите поведение функции y = 2x^2 + x - 1 при x = -3
Число F(X0) называется наибольшим значением функции на отрезке [a; b],
13
если
14
Что называется асимптотой кривой?
#
Вопрос
Ответ
Статус
кривой до
этой прямой
стремится к
нулю при
удалении
точки М в
бесконечность
15
2
Найдите
Не
верно
#
Вопрос
16
Ответ
Статус
2
Не
верно
3
Не
верно
3
Не
верно
Найдите
17
Вычислите определенный интеграл
18
Вычислите определенный интеграл
#
Вопрос
19
Ответ
Статус
3
Не
верно
-2
Не
верно
3
Не
верно
2
Не
верно
Вычислите определенный интеграл
20
Вычислите определенный интеграл
21
Укажите какая из сумм является интегральной
22
Найдите площадь фигуры, ограниченной линиями y = 6x – x^2, y = 0
#
Вопрос
23
Ответ
Статус
3
Не
верно
2
Не
верно
1
Верно
3
Не
верно
Найдите площадь фигуры, ограниченной линиями
24
Найдите общее решение уравнения (x + y)dx + xdy = 0
25
Найдите общее решение уравнения
Найдите общее решение
26
уравнения
#
Вопрос
Ответ
Статус
2
Не
верно
4
Не
верно
расходится
Верно
2
Не
верно
Среди перечисленных дифференциальных уравнений укажите линейное
27
уравнение
Укажите общее решение
28
уравнения
29
Исследуйте ряд на сходимость
30
Найдите радиус сходимости ряда