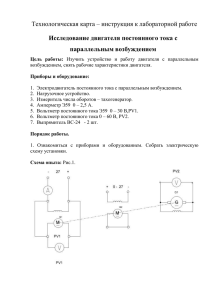
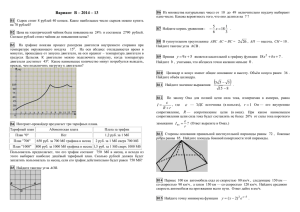
Eп kя Tя s + 1 Iя Eя Rш kM 1 Mс Mдин M 1 Js ω kE Rп Основная литература • Ковчин С.А., Сабинин Ю.А. Теория электропривода: Учебник для вузов. — СПб.: Энергоатомиздат. Санкт-Петербургское отделение, 1994 (2000). • Соколовский Г.Г. Электроприводы переменного тока с частотным регулированием: учебник для студентов ВУЗов. — М.: Изд. центр «Академия», 2006/2007. • Ильинский Н.Ф., Козаченко В.Ф. Общий курс электропривода: Учебник для вузов: — М.: Энергоатомиздат., 1992. • Методические указания к практическим занятиям по дисциплине «Теория электропривода» / Сост. А.И. Косарев, Г.Г. Соколовский, В.М. Стасовский. ГЭТУ. СПб, 1997. Дополнительная литература • Ильинский Н.Ф. Общий курс электропривода: Учебник для вузов: — М.: Издательский дом МЭИ, 2007. • Ключев В.И. Теория электропривода. Учебник для вузов. — М.: Энергоатомиздат. 1985 • Водовозов В.М. Теория и системы электропривода. Изд-во СПбГЭТУ «ЛЭТИ», 2004. • Башарин А.В., Новиков В.А., Соколовский Г.Г. Управление электроприводами: Учебное пособие для вузов. — Л.: Энергоатомиздат, 1982. • Сабинин Ю.А. Позиционные и следящие электромеханические системы: Учебное пособие для вузов. — СПб.: Энергоатомиздат, Санкт-Петербургское отделение, 2001. • Онищенко Г.Б. Электрический привод. Учебник для вузов — М.:РАСХН. 2003. 2 Тема №1 Электропривод как система Определение электропривода, структурная схема электропривода. Основные термины, используемые в технике электропривода. Лекция №1 Понятие и структура электропривода. В настоящее время действует стандарт ГОСТ Р 50369–92 «Электроприводы. Термины и определения»1 . Определение. Электропривод — это электромеханическая система, состоящая в общем случае из взаимодействующих преобразователей электроэнергии, электромеханических и механических преобразователей, управляющих и информационных устройств и устройств сопряжения с внешними электрическими, механическими, управляющими и информационными системами, предназначенная для приведения в движение исполнительных органов рабочей машины и управления этим движением в целях осуществления технологического процесса. Структурная схема электропривода приведена на рис. 1. Механическая часть Источник питания Возмущение Силовая часть Управление УУ ПЭ Система управления ЭД МП Исполн. орган рабоч. машины ИУ Электропривод Рис. 1. Структурная схема электропривода. Источник энергии (ИЭ) — это как правило, промышленная сеть. В ряде случаев (на судах, самолётах), может быть автономным, т. е. аккумуляторной батареей или генератором. Определение. Преобразователь электрической энергии (ПЭ) — это электротехническое устройство, преобразующее электрическую энергию с одними значениями параметров и/или показателей качества в электрическую энергию с другими значениями параметров и/или показателей качества. Под параметрами энергии понимаются такие, как частота, напряжение и ток, число фаз. Например, некоторые мощные асинхронные двигатели имеют две обмотки типа «звезда», сдвинутые друг относительно друга на 30 электрических градусов, и требуют соответствующего шестифазного питания, а сеть поставляет только трёхфазное. Другой пример. Для работы двигателя постоянного тока требуется постоянное напряжение, для чего ставится преобразователь, выпрямляющий сетевое напряжение. Основное назначение преобразователя состоит в формировании управляемого потока энергии, потребляемого рабочим процессом. Соответственно, для двигателей постоянного тока преобразователи должны обеспечивать постоянное напряжение, величина которого может регулироваться управляющим устройством, а для асинхронных двигателей преобразователи должны обеспечивать регулирование напряжения как по его величине, так и по частоте. В прошлом в качестве преобразовательных устройств ПЭ использовались электромашинные преобразователи, потом появились ртутные на основе игнитронов. В настоящее время преимущественно используются полупроводниковые преобразователи: тиристорные управляемые выпрямители (УВ), транзисторные и тиристорные инверторы и преобразователи частоты. Определение. Двигатель (ЭД) — это электромеханический преобразователь, предназначенный для преобразования электрической энергии в механическую. Двигатель используется для формирования (совместно с механической передачей) заданных форм движения рабочих органов. В некоторых режимах двигатель может выполнять и обратное преобразование. 1 Данный стандарт введён в РФ впервые с 1994. До него действовал разработанный в СССР ГОСТ 16593–79 «Электроприводы. Термины и определения.» C 1994 года ГОСТ 16593–79 в РФ отменён. 3 Определение. Механическая передача (МП) — это механический преобразователь, предназначенный для передачи механической энергии от электродвигателя к исполнительному органу рабочей машины и согласования вида и скорости их движения. Заметим, что в тормозных режимах энергия может передаваться обратно к электродвигателю. Необходимость в механическом преобразователе рассмотрим на следующем примере [?]. Номинальная мощность электродвигателя Pном определяется выражением Pном = Mном ωном , где Mном — номинальный вращающий момент на валу ротора; ωном — номинальная угловая скорость ротора. В свою очередь Mном = Cк D 2 L, где Cк — коэффициент, зависящий от конструктивных особенностей электрической машины; D — диаметр якоря; L — длина активной части якоря. Отсюда следует, что для уменьшения габаритов двигателя (D 2 L) при заданной мощности необходимо увеличивать угловую скорость ωном . Обычно, для большинства применяемых в промышленности двигателей nном = 1000 . . . 6000 об/мин. В то же время для рабочих машин по технологическим условиям требуется скорость меньшая примерно в 10 . . . 100 раз. Согласование механических параметров электродвигателя (скорости и момента) с механическими параметрами рабочей машины осуществляется при помощи механической передачи (МП). При этом МП может изменять характер движения, преобразуя вращательное движение в поступательное. Определение. Информационное устройство (ИУ) — это устройство, предназначенное для получения, преобразования, хранения, распределения и выдачи информации о переменных электропривода, технологического процесса и сопредельных систем для использования в системе управления электропривода и внешних информационных системах. Определение. Управляющее устройство электропривода (УУ) — это устройство, предназначенное для формирования управляющих воздействий в ЭП. При необходимости, в ЭП предусматриваются устройства сопряжения, обеспечивающие взаимодействие с сопредельными системами отдельных частей ЭП. (На рис. не показаны.) Определение. Устройство сопряжения (электропривода) — это совокупность электрических и механических элементов, обеспечивающих взаимодействие электропривода с сопредельными системами и отдельных частей электропривода. Определение. Система управления электропривода — это совокупность управляющих и информационных устройств и устройств сопряжения электропривода, предназначенных для управления электромеханическим преобразованием энергии с целью обеспечения заданного движения исполнительного органа рабочей машины. Определение. Система управления электроприводом — это внешняя по отношению к ЭП система управления более высокого уровня, поставляющая информацию, необходимую для функционирования ЭП. При рассмотрении ЭП будем выделять механическую часть ЭП, относя к ней подвижный орган электрической машины, механическую передачу и исполнительный орган (который формально не входит в состав ЭП). При этом не рассматривается то обстоятельство, что движущий момент создаётся электромагнитными процессами в двигателе. Это даёт возможность отдельно рассматривать механику электропривода. Поскольку процессы, происходящие в исполнительном органе, который формально не входит в понятие «электропривод», оказывают на него существенное воздействие, в целом ряде случаев нельзя обходиться без учёта этих процессов. Практически все элементы электропривода должны быть вам известны из предыдущих курсов. Основные свойства ЭП проявляются в нём как в системе, объединяющей все элементы и предназначенной для целенаправленного приведения в движение рабочих органов машины, т. е. решения задачи управления. ГОСТ 50369–92 предусматривает деление электроприводов на несколько групп по различным признакам, некоторые из которых рассмотрены ниже. 1. По функциональному назначению приводы делятся на главные и вспомогательные. Главный привод обеспечивает движение исполнительного (рабочего) органа рабочей машины и основную операцию процесса. Вспомогательный привод обеспечивает движение вспомогательных органов машины. 2. По способу разделения энергии электроприводы делятся на а) групповой, б) индивидуальный, в) взаимосвязанный и г) многодвигательный. Определение. Групповой электропривод — это электропривод с одним электродвигателем, обеспечивающий движение исполнительных органов нескольких рабочих машин или нескольких исполнительных органов одной рабочей машины. Наиболее ярким примером здесь является швейная машинка, в которой перемещение иглы, ткани и шпули осуществляется от одного двигателя. 4 Определение. Индивидуальный электропривод — это электропривод, обеспечивающий движение одного исполнительного органа рабочей машины. В системах индивидуального электропривода энергия разделяется в электрических цепях, что позволяет существенно упростить передаточные устройства привода и кинематику рабочей машины, что снижает металлоёмкость оборудования, повышает его надёжность при надлежащей настройке, хотя часто усложняет автоматизацию процессов управления движениями исполнительных органов. Определение. Взаимосвязанный электропривод — это два или несколько электрически или механически связанных между собой электроприводов, при работе которых поддерживается заданное соотношение их скоростей и/или нагрузок, и/или положения исполнительных органов рабочих машин. В качестве примера можно привести электропривод многоклетьевого проволочного стана, когда рабочие валки механически связаны между собой через прокатываемую заготовку, а задачей электропривода является поддержание заданного соотношения скоростей между валками. Определение. Многодвигательный электропривод — это электропривод, содержащий несколько электродвигателей, механическая связь между которыми осуществляется через исполнительный орган рабочей машины. Например, два двигателя могут работать на общий вал редуктора, с целью уменьшения суммарного момента инерции. ГОСТ различает ЭП с разомкнутой и с замкнутой системами управления. Определение. Электропривод с разомкнутой системой управления — это электропривод, в котором отсутствует обратная связь по регулируемой координате электропривода или по возмущению, воздействующая на управляющее устройство. В данном случае ЭП включает в себя преобразователь, двигатель и механическую передачу, которые составляют силовую часть привода. Если такая связь имеется, то электропривод называется электроприводом с замкнутой системой управления. Требования, предъявляемые к электроприводу 1. Надёжность. 2. Точность, т. е. обеспечение приводом отклонения какого-либо параметра от заданного значения не выше допустимого. Может идти речь о точности поддержания той или иной координаты, например, скорости, точности позиционирования, точности воспроизведения исполнительным органом заданной траектории и т. д. 3. Быстродействие, т. е. способность системы за минимально возможное время отработать задающие воздействие или восстановить требуемое значение координаты при действии на систему внешних возмущений. 4. Поскольку, говоря о быстродействии мы оцениваем динамические качества системы, важным является качество динамических процессов, т. е. обеспечение определённого характера их протекания. 5. Энергетическая эффективность, т. е. малые потери. 6. Совместимость с системой энергоснабжения, т. е. минимальное влияние электропривода на источник питания. 7. Ресурсоёмкость, т. е. минимальная материалоёмкость и энергоёмкость. 5 Тема №2 Механическая часть силового канала электропривода Кинематическая и расчётная схемы механической части электропривода. Инерционные свойства элементов механической части. Характеристики сил и моментов, действующих на электропривод. Приведение моментов, сил и параметров механической части электропривода к одному валу. Одномассовая и двухмассовая механические системы. Характер движения механической системы при воздействии на неё внешних моментов. Определение момента инерции и массы элементов кинематической схемы электропривода. Приведение инерционных масс, моментов, усилий коэффициентов жёсткости и разных форм движения к одному валу. Прежде всего, заметим, что, занимаясь разработкой электропривода, вам придётся иметь дело с кинематическими схемами (читать или изображать их в своей документации). Элементы кинематики должны обозначаться по ГОСТ 2.770–68 «ЕСКД. Обозначения условные графические в схемах. Элементы кинематики.» А также в соответствии с ГОСТ 2.721–74 «ЕСКД. Обозначения условные графические в схемах. Обозначения общего применения.» Итак, ЭП, как ЭМС, может быть разделён на первом этапе на механическую и электрическую части. Начиная рассмотрение с механической части, отметим, что должен знать и уметь инженер в области механики ЭП: • знать общие особенности механической части ЭМС, их элементы, связи, параметры, методы описания и анализа; • уметь на основе известной кинематики механизма, его технологических данных и сведений о технологическом процессе составить расчётные схемы; • уметь рассчитывать параметры механической части ЭП; • уметь описывать движение механической части системой дифференциальных уравнений, строить соответствующие частотные характеристики, и оценивать механические переходные процессы. Представление о движущихся массах механической части и связях между ними даёт кинематическая схема механизма. Очевидно, что при огромном разнообразии механизмов и их механические схемы будут различны. Однако можно отметить характерные элементы, присутствующие в большинстве механизмов: • якорь (или ротор) двигателя, на который действует развиваемый двигателем момент; • ряд зубчатых передач, образующих понижающий редуктор; • соединительные муфты; • собственно, исполнительный орган. [?] По конструкции передаточные механизмы весьма разнообразны. Далее рассмотрим некоторые их виды (рис. 2). Редукторы Определение. Редуктор — это механизм для уменьшения частоты вращения и увеличения крутящего момента, в котором не менее двух звеньев сопряжены зубчатыми или червячными зацеплениями1 . Они бывают различных конструкций, из которых наиболее часто используются цилиндрические, конические и червячные редукторы. Конические редукторы отличаются от цилиндрических тем, что у них можно выходной вал разместить под углом ко входному. Червячные редукторы состоят из червяка и зубчатого колеса. Они позволяют получать очень большие передаточные отношения в небольших габаритах по сравнению с цилиндрическими. Недостатком является низкий КПД и меньший, чем у зубчатых редукторов, ресурс, в связи с чем их рекомендуется применять в машинах непрерывного действия. Кроме того, они обладают свойством самоторможения, т. е. передают момент только от двигателя к исполнительному механизму, что является в ряде случаев положительным свойством. Основными характеристиками редукторов являются максимальный крутящий момент на выходном (тихоходном) валу, максимальная частота вращения, и передаточное отношение i= ω1 , ω2 1 Данное определение дано в соответствии с ГОСТ Р 50370–92. «Редукторы и мотор-редукторы общемашиностроительного применения. Термины и определения». Повышающий редуктор называется также ускорителем или мультипликатором [?] стр. 31. 6 ВСТАВИТЬ РИСУНОК ACAD2! Рис. 2. Примеры передач. где ω1 — скорость на быстроходном валу редуктора; ω2 — скорость на тихоходном валу редуктора. Передаточное число k-ой ступени редуктора равно ik = z2k , z2k−1 где z2k и z2k−1 — число зубьев на быстроходной и тихоходной шестернях, соответственно. Общее передаточное число редуктора равно произведению передаточных чисел всех его ступеней i = i1 · i2 . . . in . Диапазон передаточных чисел одноступенчатого редуктора составляет i = l,6 . . . 8, двухступенчатых — i = 7,1 . . . 50 (обычно i = 8 . . . 40), трёхступенчатых — i = 25 . . . 250 (обычно i = 31,5 . . . 180). Ременные (цепные) передачи характеризуются передаточным числом j= ω1 D2 Z2 = = , ω2 D1 Z1 где D1 и Z1 — диаметр и число зубьев входного шкива (звёздочки); D2 и Z2 — диаметр и число зубьев выходного шкива (звёздочки). Передачи зубчатое колесо–рейка и барабан–трос преобразуют вращательное движение в поступательное и характеризуются радиусом приведения ρ, м/рад ρ= v D = . ω 2 Винтовая и червячно-реечная передачи преобразуют вращательное движение винта (червяка) в перемещение гайки (рейки). Радиус приведения поступательного движения к вращательному: а) для винтовой передачи v l tш ρ= = = , ω ϕ 2π б) для червячно-реечной передачи ρ= tр Zч v l = = , ω ϕ 2π где l, v — линейные перемещение и скорость; ϕ, ω — угловые перемещение и скорость; tш , tр — шаг винта и шаг рейки; Zч — число заходов червяка. 7 Поворот винта на один оборот приводит к перемещению гайки на один шаг. Для перехода от кинематической схемы к расчётной схеме обратимся к примеру электропривода механизма (рис. 3). 2 1 9 6 11 7 3 8 5 4 F Mд 10 12 Рис. 3. Пример кинематической схемы. На кинематической схеме обозначены: 1 — якорь; 2 — редуктор с зубчатыми зацеплениями 9, 10, 11, 12 ; 3 — промежуточный вал; 4 — винтовая передача; 5 — исполнительный орган; 6, 7, 8 — муфты. Механическая часть ЭП включает в себя связанные между собой движущиеся части: якорь (ротор) ЭД, элементы кинематической связи и исполнительный орган. Отдельные элементы схемы вращаются с разными скоростями, а исполнительный орган совершает поступательное движение. Каждый элемент схемы представляет собой инерционное звено, характеризуемое массой или моментом инерции. При нагружении отдельные элементы механизма, не обладающие абсолютной жёсткостью, деформируются. Кинематическая схема является исходной для расчёта механики электропривода, который выполняется на основе расчётной схемы механической части. При переходе от кинематической к расчётной схеме необходимо принимать во внимание следующие положения • Элементы механической части вращаются с различными скоростями; • Наряду с вращающимися частями могут быть элементы, совершающие поступательное движение; • Моменты и усилия могут прикладываться к различным элементам механической части; • Упругая деформация носит обычно распределённый характер; • В кинематических передачах имеют место зазоры и трение; • На отдельные элементы кинематической схемы действуют силы и моменты сопротивления. В связи с этим, переход к расчётной схеме связан с введением определённых допущений и упрощений. К их числу могут относиться следующие: • механическая часть представляется в виде системы с сосредоточенными массами, все элементы которой делятся на элементы, в которых сосредоточены массы, и которые считаются абсолютно жёсткими, и на упругие связи между ними. • представление о том, что силы и моменты действуют только на сосредоточенные массы и не действуют на упругие связи. • в тех случаях, когда это возможно, пренебрежение зазорами в кинематических цепях. • упрощение характера сил трения, а иногда и пренебрежение трением. В расчётной схеме все скорости, моменты инерции, массы, моменты сил, усилия и коэффициенты жёсткости приводятся к одной оси — валу двигателя. Т. е. заменяется схемой вида рис. 4. Движение каждой механической части подчиняется второму закону Ньютона. При данных значениях сил или моментов, действующих на элемент, ускорение его будет зависеть от его инерционности. Мерой инерционности тела для поступательного движения является масса m, выраженная в кг, а для вращательного движения — момент инерции, J, в кг · м2 . В старых справочниках, каталогах и др. литературе вместо момента инерции использовался маховый момент GD 2 . Маховый момент равен учетверённому моменту инерции GD 2 = 4J. J1 8 J3 J2 Рис. 4. Расчётная схема электропривода. Момент инерции тела при вращении его относительно оси определяется суммой произведений масс mi малых частей тела на квадраты расстояний ri от этих частей до оси J= k X mi ri2 . i=1 Для тел простой формы формулы расчёта моментов инерции можно найти в справочниках. Эти формулы, как правило, приводятся для вращения вокруг оси, проходящей через центр масс детали. В том случае, когда ось вращения не проходит через центр масс детали, момент инерции рассчитывается по формуле Jд = Jд0 + mд r 2 , где Jд — момент инерции детали, относительно заданной оси; Jд0 — момент инерции детали относительно оси, проходящей через центр масс и параллельной заданной оси; mд — масса детали; r — расстояние от центра масс детали до оси. Моменты инерции шкивов тормозов, роторов двигателей часто приводятся в каталогах. На практике часто моменты инерции сложных деталей проектировщику электропривода не задаются, и определять их приходится непосредственно по рабочим чертежам. Для этого определяется ось вращения детали, деталь разбивается на участки, для которых момента инерции можно найти по таблицам. Затем моменты инерции вычисляются и складываются с учётом расстояний до оси вращения. В практических расчётах вводится понятие радиуса инерции ρ. Определение. Радиусом инерции тела называется такое расстояние от оси до материальной точки с массой, равной массе тела, при котором она имеет такой же момент инерции относительно данной оси, как и это тело. В этом случае n n X X mi ri2 = mρ2 , mi . Jт = m= i=1 i=1 Часто в таблицах приводятся не сами моменты инерции, а радиусы инерции. Если тело вращается относительно оси, не проходящей через его центр масс, то его радиус инерции определяется из соотношения ρ2т = ρ2т0 + r 2 , где ρт — радиус инерции относительно данной оси; ρт0 — радиус инерции относительно оси, проходящей через центр масс тела и параллельной данной оси; r — расстояние между этими осями. Упругие свойства элементов расчётной схемы Теоретически все элементы механической части не обладают абсолютной жёсткостью и при нагружении деформируются. Если рассматривать эти деформации как упругие и подчиняющиеся закону Гука, который гласит, что в области упругих деформаций величина деформации прямо пропорциональна величине приложенной силы, то для оценки упругих свойств можно ввести коэффициент жёсткости c. При линейной деформации F = c · ∆l, где F — сила, Н; c — коэффициент жёсткости, Н/м; ∆l — деформация, м. Потенциальная энергия определяется выражением c · (∆l)2 . Wп = 2 При скручивании M = cϕ · ∆ϕ, где M — скручивающий момент сил, Н · м; cϕ — коэффициент жёсткости, Н · м/рад; ∆ϕ — деформация, рад. Потенциальная энергия определяется выражением Wп = cϕ · (∆ϕ)2 . 2 9 Приведение к одной оси инерционных масс, моментов, усилий и коэффициентов жёсткости Смысл приведения состоит в том, чтобы реальную кинематическую схему свести к схеме, в которой все элементы имеют одинаковый характер движения и двигаются с одинаковой скоростью. При приведении необходимо обеспечить во-первых равенство кинетической и потенциальной энергии в исходной и приведённой системах, а во-вторых равенство мощности действующих сил и моментов при выполнении перемещений в исходной и приведённой системах. Приведение момента инерции механизма к валу двигателя осуществляется исходя из равенства кинетических энергий (живых сил) в исходной и приведённой системах. 2 n Jω l X mk vk2 j j Jпр ω2д X = + , 2 2 2 j=1 k=1 откуда находим Jпр = n X Jj j=1 или Jпр = ωj ωд !2 n X Jj j=1 ij2 + l X mk k=1 + l X vk ωд !2 , mk · ρ2k , k=1 где ij — передаточное число; ρk — радиус приведения соответствующего элемента. Приведение сил и моментов сил осуществляется исходя из равенства мощностей в исходной и приведённой системе: Mпр ωд = Mω, откуда M ω = . ωд i Mпр = M · Mпр ωд = F v, откуда Mпр = F · v = F ρ. ωд Теперь приведём коэффициенты жёсткости исходя из равенства потенциальных энергий в исходной и приведённой системах. cпр (∆ϕд )2 c( ϕ∆ϕ)2 = , 2 2 где cпр — приведённая жёсткость; ∆ϕд — деформация, приведённая к валу двигателя, к которому приводим жёсткость; cϕ — реальная жёсткость; ∆ϕ — реальная деформация. cпр = cϕ (∆ϕ)2 (∆ϕд )2 и, с учётом того, что ϕд /i = ϕ, окончательно cпр = cϕ . i2 Замечание на будущее: Смысл приведения всех параметров к одной оси появляется, когда пытаются сократить число масс в упругой системе: тогда можно сравнивать жёсткости 10 Лекция №2 Временные зависимости при разгоне и торможении одномассовой механической системы. В дальнейшем будем рассматривать одномассовую жёсткую систему, в которой один из действующих на неё моментов является моментом двигателя, а другой является суммарным моментом сопротивления. В простейшем случае уравнение движения привода имеет вид Mд − Mс = Jпр εд , где Mд — момент двигателя (электромагнитный момент двигателя); Mс — момент сопротивления, приведённый к валу двигателя (статический момент); Jпр — приведённый к валу двигателя момент инерции; εд = ω̇д = ϕ̈д — угловое ускорение ротора двигателя. Из этого уравнения следует, что в установившемся (статическом) режиме алгебраическая сумма моментов должна равняться нулю, т. е. в статике все действующие на систему моменты и силы должны быть д уравновешены. Если эти два момента не равны друг другу, то εд = dω dt , 0, и в системе есть динамический режим. Разность моментов двигателя и сопротивления называется динамическим моментом Mдин = Mд − Mс . Данное уравнение справедливо в том случае, когда момент инерции постоянен. Для кривошипно-шатунных (рис. 5), кулисных и многих других механизмов момент инерции переменный и зависит от угла поворота исполнительного механизма. Выведем уравнение движения для случая, когда момент инерции зависит от угла поворота рычага исполнительного механизма ϕ. Шатун Кривошип Ползун Редуктор Муфта Двигатель Рис. 5. Кинематическая схема электропривода с кривошипно-шатунным механизмом. Выдаваемая двигателем мощность Mд ωд за вычетом потребляемой механизмом мощности Mс ωд идёт на изменение кинетической энергии Eк механизма. Mд ωд − Mс ωд = (Mд − Mс ) · ωд = С учётом того, что d d J(ϕ)ω2д Eк = ; dt dt 2 ω2д dJ(ϕ) ω2д ∂J(ϕ) dϕ 2ωд dωд d ω2д · + J(ϕ) · · = · · + J(ϕ) · . 2 dt dt 2 2 ∂ϕ dt 2 dt ωд dϕ 1 dϕд = · = , и dωд /dt = εд , получим dt i dt i (Mд − Mс ) · ωд = ω2д ∂J(ϕ) ωд · · + J(ϕ) · ωд εд . 2 ∂ϕ i И окончательно получаем Mд − Mс = J(ϕ) · εд + ω2д ∂J(ϕ) · , 2i ∂ϕ где Mд — момент двигателя; Mс — момент сопротивления механизма, приведённый к валу двигателя; J(ϕ) — момент инерции механизма, приведённый к валу двигателя, и зависящий от угла поворота механизма 11 ϕ; εд — угловое ускорение вала двигателя; ωд — угловая скорость вала двигателя; i — передаточное ∂J(ϕ) число редуктора; — производная момента инерции по углу поворота исполнительного механизма, ∂ϕ приведённая к валу двигателя. Данному дифференциальному уравнению соответствует структурная схема, приведённая на рис. 6 (сплошные линии). Для выполнения расчётов данную структурную схему можно набрать в пакетах моделирования, например, в Simulink. Поскольку как при наборе модели, так и при вычислении производных могут возникать ошибки, целесообразно проверять правильность работы модели. Для этого в модель можно ввести дополнительные блоки (изображённые пунктирной линией), которые вычисляют кинетическую энергию меR ханизма Eк0 = J(ϕ)ω2д /2, и затраченную энергию Eк00 = (Mд − Mс ) · ωdt. Графики обоих величин должны совпадать. Если графики не совпадают, то это говорит или об ошибке в модели, или о том, что нужно использовать более точный метод интегрирования. ∂J(ϕ) ∂ϕ Mс (ϕ, ω, t, . . .) Mд ω2д 2i 1 s ωд 1 s ϕд ϕ 1 i 1 J(ϕ) x= 1 J(ϕ) Eк0 ω2д 2 1 x J(ϕ) 1 s Eк00 Рис. 6. Структурная схема механической части электропривода при переменном моменте инерции. Характеристики сил и моментов, действующих на механическую систему Силы и моменты, действующие на систему делятся на • активные и • реактивные (пассивные). Активные силы и моменты могут быть движущими, т. е. способствовать движению (например, при опускании груза), или быть силами и моментами сопротивления, т. е. препятствовать движению (например, при подъёме груза или сжатии упругой пружины). Они обусловлены внешними источниками энергии и действуют на механическую систему независимо от её движения. Активные моменты характеризуются тем, что направление их действия не зависит от направления движения, они могут сохранять свой знак при изменении знака скорости и менять свой знак при неизменном знаке скорости. Пример механической части привода с активным моментом и механическая характеристика приведены на рис. ?? 12 В свою очередь, реактивные (пассивные) силы и моменты всегда являются моментами сопротивления. Они возникают как реакция на движение и всегда препятствуют ему. Энергия пассивных нагрузок расходуется на трение скольжения и качения, на пластическую деформацию материала, например, при прокатке и т. д. Пассивные силы и моменты всегда рассеивают энергию, т. е. являются диссипативными. Примеры пассивных моментов сопротивления приведены на рис. 8 ω Механическая характеристика двигателя M = Fr M Характеристика момента силы тяжести 0 m F = mg а б Рис. 7. Пример механизма, создающего активный момент а и механическая харктеристика активного момента б. ω ω M Момент, не зависящий от скорости Mс = Mс0 sign ω ω M Момент сухого трения ω M Момент сил трения в упругих элементах Mс = kω ω M Момент вязкого трения Mс = (M0 + kω2 ) sign ω M Суммарный момент сухого и вязкого трения Рис. 8. Примеры пассивных моментов. В общем случае статический момент для центробежных роторных машин — центрифуг и насосов, работающих с постоянным напором определяется выражением Mс = M0 + k|ω|l · sign(ω), где l может принимать различные значения, в том числе и дробные, и может достигать для высокоскоростных установок пяти. Поведение механической одномассовой системы при воздействии на неё динамических моментов Рассмотрим одномассовую систему с суммарным приведённым к валу двигателя моментом инерции J. На вал двигателя действует электромагнитный момент Mд и приведённый момент сопротивления Mс . В начальный момент времени вал вращается со скоростью ωд0 . Движение вала двигателя описывается уравнением Mд − Mс = J dωд . dt 13 ω, M ω M t1 t2 t Картинку дорисовать Рис. 9. Графики скорости и момента при реверсе электропривода с пассивным моментом. В этом уравнении момент двигателя и момент сопротивления при одинаковых знаках направлены в противоположные стороны. При Mд = Mс вал вращается с постоянной скоростью ω = ωд0 . При Mд , Mс , Mд = const Mс = const, вал вращается с ускорением (при Mд > Mс , или с замедлением при Mд < Mс ), равным dωд Mд − Mс = . dt J Время разгона от скорости ωд0 до скорости ωд1 составляет tразг = J · ωд1 − ωд0 . Mд − Mс Рассмотрим случай реверса, когда момент сопротивления зависит от направления вращения вала двигателя (Mс = k sign ωд ). До момента t = 0 двигатель вращается со скоростью ωд0 , момент двигателя уравновешивает момент сопротивления (Mд1 = Mс ). В момент t = 0 начинается реверс. Момент двигателя изменяет знак, и становится равным минус Mд2 . При этом к валу двигателя прикладывается суммарный динамический момент, равный Mдин1 = −Mд2 −Mс . Скорость двигателя снижается до нуля за время торможения tт = J · ωд0 . Mдин1 Далее, когда скорость меняет свой знак, меняет свой знак и момент сопротивления. Вал двигателя начинает раскручиваться в обратную сторону под действием динамического момента Mдин2 = −Mд2 + Mс . Заметим, что, чтобы привод стал вращаться в обратную сторону, момент двигателя по абсолютной величине должен превышать момент сопротивления |Mд2 | > |Mс |. Когда вал двигателя достигнет требуемой скорости ω2 через время разгона ωд0 , tр = J · Mдин2 момент двигателя снижается до величины Mд3 = Mс . При этом, динамический момент равен Mдин3 = −Mд3 + Mс = −Mс + Mс = 0, и скорость двигателя не изменяется. Как нетрудно заметить, общее время реверса составляет ! ωд0 ωд1 tрев = tт + tр = J · + . Mд2 + Mс Mд2 − Mс Реверс при подъёме грузов (активный момент). Рассмотрим подъём груза m1 краном с противовесом m2 . Пусть m1 > m2 . На трос будут действовать противоположно направленные силы F1 = m1 g и F2 = m2 g. Статический момент, который преодолевает привод, определяется выражением Mс = (m1 − m2 )gR, R ωд 14 ω ωд0 Mд Mс t m1 m2 ωд1 F1 F2 Рис. 10. Пример механизма а и графики скорости и момента б при реверсе электропривода с активным моментом.. где R — радиус барабана. Исходно момент сопротивления уравновешивается моментом двигателя Mд0 : Mд0 = Mс , динамический момент равен нулю. Барабан вращается со скоростью ωд0 , и груз m1 поднимается. В момент времени t0 начинается реверс. Для этого момент двигателя снижается до величины 0 < Mд1 < Mс . Динамический момент, определяемый как Mдин1 = Mд1 − Mс становится отрицательным, и барабан Mдин1 . Подъём груза идёт с замедлением a = Rε начинает тормозиться с ускорением ε = J Через промежуток времени t1 − t0 = ωд0 /ε скорость барабана снижается до нуля, и подъём груза m1 заканчивается. После этого барабан начинает разгоняться в противоположную сторону с тем же самым ускорением ε, а груз начинает спускаться с ускорением a. Когда в момент времени t2 скорость опускания груза достигает требуемой величины ωд1 , момент двигателя Mд устанавливается равным моменту сопротивления Mс . При этом динамический момент становится опять равным нулю, барабан начинает вращаться с постоянной скоростью ωд1 , а груз — опускаться без ускорения. Разгон при Mс , const и зависящим от скорости Как Mс , так и Mд могут меняться в зависимости от скорости по определённому закону. Рассмотрим разгон при Mд = const и Mс , линейно зависящим от скорости. Итак, пусть Mс = kωд , тогда dωд Mд − kωд = J . dt В операторной форме это уравнение будет иметь вид Mд (p) − kωд (p) = Jpωд (p); Mд (p) = (Jp + k)ωд (p); ωд (p) = Mд (p) 1 1 . k kJ p + 1 В том случае, когда момент имеет форму единичного ступенчатого воздействия 0, при t < 0 Mд (t) = M, при t 6 0 разгон будет производиться до скорости ω = M/k по апериодическому закону с постоянной времени T = J/k. В более сложных случаях составляются соответствующие дифференциальные уравнения, которые затем и решаются тем или иным методом численного интегрирования. Ранее это были графоаналитические методы, моделирование на аналоговых вычислительных машинах. В настоящее время дифференциальные уравнения решаются численно в соответствующих математических пакетах, например, строится модель в Simulink. В реальных механизмах, момент сопротивления на валу двигателя изменяется по случайному закону. Механическая система, на которую действует случайный момент, строго говоря, всё время находится в неустановившемся режиме. В литературе часто говорится о необходимости использования методов теории случайных процессов, в тех случаях, когда случайная составляющая момента сопротивления имеет ярко 15 выраженный характер, и ей нельзя пренебречь. На практике, при разработке техники гражданского назначения, инженеры просто рассчитывают систему на наиболее худший или на наиболее вероятный вариант, и принимают его с некоторым запасом. 16 Лекция №3 Двухмассовая упругая механическая система и её реакция на ступенчатое управляющее воздействие. Ранее мы рассматривали механическую часть электропривода как «жесткую» машину. То есть, все звенья представлялись телами, которые незначительно деформируются в процессе движения, вследствие чего этой деформацией можно пренебречь; кинематические связи между отдельными элементами машины принимались абсолютно жесткими; кинематические пары не имеют люфтов и зазоров, идеально реализуются те уравнения связи, которыми они описываются, т. е. пары рассматриваются как голономные1 удерживающие связи. Степень подвижности жесткой машины определяется числом взаимосвязанных приводов, обеспечивающих ее движение. При индивидуальном приводе имеется всего одна степень свободы. В действительности, в механической части привода возникают деформации реальных кинематических связей и пар и перераспределение потенциальной энергии, вызывающее различные вибрации, которые называют упругими колебаниями. Эти колебания приводят к дополнительным динамическим нагрузкам в отдельных звеньях и влияют на точность работы исполнительных механизмов. Поэтому для исследования этих явлений приходится рассматривать динамическую модель электропривода как механизм с упругими звеньями — «упругую машину». В расчётах учитывать распределённый характер упругостей и масс довольно проблематично, поэтому, обычно строится модель упругой машины из абсолютно жёстких элементов с сосредоточенными массами (моментами инерции), соединённых безинерционными упругими связями. При этом число элементов стараются свести к минимуму. Рассмотрим двухмассовую механическую систему рис. 11. cϕ J1 Mд ω1 J2 M12 M12 Mс ω2 Рис. 11. Двухмассовая система. Система содержит две вращающиеся массы с моментами инерции J1 и J2 , связанные упругим звеном с жёсткостью cϕ . К первой массе (пусть это будет ротор двигателя) приложен момент двигателя Mд , а ко второй — статический момент Mс . В статическом режиме все элементы системы будут двигаться с постоянной скоростью ω1 . В динамическом же режиме из-за наличия упругости скорости будут различны: ω1 — у первой массы и ω2 — у второй. Составим уравнения движения двухмассовой системы. Рассмотрим первую массу. На неё действует электромагнитный момент двигателя Mд и реакция упругого элемента M12 . Движение этой массы описывается уравнением dω1 . Mд − M12 = J1 dt На вторую массу действуют момент сопротивления Mс и момент упругого элемента M12 , соответственно уравнение движения имеет вид dω2 . M12 − Mc = J2 dt Реакция упругого элемента описывается уравнением Z M12 = cϕ · (ϕ1 − ϕ2 ) = cϕ ω1 − ω2 dt. 1 Голономными называются такие механические системы, в которых все связи являются геометрическими (голономными), т. е. налагающими ограничения только на положения (или перемещения за время движения) точек и тел системы, но не на величины их скоростей. 17 Перепишем эти уравнения в виде следующей системы dω1 1 = · (Mд − M12 ), dt J 1 dM12 = cϕ · (ω1 − ω2 ), dt dω2 1 = · (M12 − Mс ). dt J2 Этой системе соответствует структурная схема, приведённая на рис. 12. Mс Mд ω1 − ω2 ω1 1 J1 s cϕ s M12 1 J2 s ω2 Рис. 12. Структурная схема двухмассовой системы. Полученная математическая модель может использоваться для расчёта динамики, вместе с тем часто бывает удобно располагать передаточными функциями, связывающими координаты системы с внешними воздействиями. Для двухмассовой упругой системы может быть записано шесть передаточных функций, связывающих её выходные координаты ω1 , ω2 , M12 с двумя внешними воздействиями Mд и Mс . Мы получим две передаточных функции, одна из которых связывает с моментом двигателя скорость второй массы, а другая — скорость первой массы. ω2 Чтобы получить передаточную функцию Wд2 = выполним преобразования структурной схемы Mд рис. acad5. Этой структурной схеме соответствует передаточная функция Wд2 (s) = cϕ J1 J2 s3 cϕ 1 1 = = · . cϕ 3 + c · (J + J )s J J (J + J )s J J s 1 2 1 2 1 2 ϕ 1 2 2 · (J + J )s 1+ s + 1 1 2 J1 J2 s3 (J1 + J2 )cϕ Теперь получим передаточную функцию Wд1 = ω1 выполним структурные преобразования рис. 13. Mд J1 s Mд 1 J1 s cϕ s Mд J2 s cϕ J2 s2 + cϕ J2 s ω2 1 J2 s 1 J2 s Рис. 13. Структурные преобразования схемы двухмассовой системы. Этой структурной схеме соответствует передаточная функция Wд1 (s) = 1 J1 s 1+ 1 J1 s · J2 cϕ s cϕ +J2 s2 = cϕ + J2 s2 cϕ + J2 s2 = = J1 s(cϕ + J2 s2 ) + J2 cϕ s J1 scϕ + J1 J2 s3 + J2 cϕ s ω1 18 = 1 + cJ2ϕ s2 1 + cJ2ϕ s2 cϕ + J2 s2 1 = . = · (J1 + J2 )s 1 + J1 J2 s2 (J1 + J2 )cϕ s + J1 J2 s3 (J1 + J2 )s + Jc1ϕJ2 s3 cϕ (J1 +J2 ) Полученные передаточные функции содержат колебательное звено, следовательно, любое воздействие будет приводить к появлению незатухающих колебаний. J1 J2 Величина (J1 +J = Tу2 измеряется в секундах в квадрате. Tу называется постоянной времени упругости. 2 )cϕ Величину J2 /cϕ можно представить в виде J2 J1 J2 1 J1 + J2 = · · = Tу γ, cϕ J1 + J2 cϕ J1 J1 + J2 — коэффициент соотношения масс. J1 Введём обозначение J = J1 + J2 и запишем передаточные функции в следующем виде где γ = Wд1 (s) = Wд2 (s) = 2 2 ω1 (s) 1 γTу s + 1 = · 2 2 ; Mд (s) Js Tу s + 1 ω2 (s) 1 1 = · 2 2 . Mд (s) Js Tу s + 1 Построим логарифмические частотные характеристики этих передаточных функций Рис. 14. Логарифмические характеристики первой Lд1 и второй массы Lд2 двухмассовой системы. ЛАХ одномассовой системы L0 . На графике обозначены: Lд1 — логарифмическая частотная характеристика функции Wд1 ; Lд2 — ЛАХ 1 функции Wд2 ; L0 — ЛАХ соответствующей одномассовой системы с передаточной функцией W0 (s) = . Js Из рассмотрения выражений и ЛАХ можно сделать следующие выводы: 1. Характеристики одномассовой и двухмассовой систем не отличаются друг от друга в области нижних частот. Это значит, что при медленных изменениях момента Mд эти две системы ведут себя одинаково. 2. В области верхних частот характеристика Lд1 проходит выше характеристики Lд2 . Это объясняется тем, что при появлении на входе системы момента Mд , сначала приходит в движение первая масса, а затем начинает двигаться вторая. 3. Наличие в передаточных функциях знаменателя (Tу2 s2 + 1) указывает на колебательный характер движения. Поскольку при рассмотрении двухмассовой системы мы не учитывали моменты трения, возникающие колебания не будут затухать. В реальной механической системе за счёт наличия диссипативных сил затухание будет иметь место, что найдёт своё отражение в том, что колебательное звено второго порядка в знаменателе будет иметь слагаемые с s. В зависимости от физической природы диссипативные силы делят на два класса: силы внутреннего трения в материалах упругих элементов и силы внешнего трения, возникающие в местах соединения отдельных 19 элементов упругих звеньев вследствие их конструктивного исполнения. Например, при соединении вала с зубчатым колесом с натягом в контактной поверхности вала и ступицы колеса возникают силы нормального давления. При скручивании вала проявляется действие диссипативных сил. Точный учет действия диссипативных сил затруднён вследствие влияния на них множества случайных факторов, поэтому обычно в теории электропривода их учитывают приближенно введением коэффициента сопротивления b. Тогда реакция упругого элемента M12 будет равна M12 = Mу + Mсд = cϕ · (ϕ1 − ϕ2 ) + b · (ω1 − ω2 ). где cϕ — жесткость; b — коэффициент сопротивления; Mу и Mсд — моменты упругих и диссипативных сил соответственно. В практических расчетах вместо жесткости cϕ иногда используют обратную величину e = 1/cϕ , которую называют податливостью. В этой формуле множитель (ω1 − ω2 ) соответствует скорости изменения угла закручивания ϕ = ϕ1 − ϕ2 . Соответствующая структурная схема приведена на рис. 15. Mд 1 J1 s ω1 Mс ω1 − ω2 M12 cϕ s 1 J2 s ω2 b Рис. 15. Структурная схема двухмассовой системы с учётом диссипативных сил. Двухмассовая механическая система при воздействии ступенчатого изменения момента на первой массе. Предполагая, что момент, действующий на первую массу, есть момент двигателя Mд , воспользуемся передаточными функциями 2 2 ω1 (s) 1 γTу s + 1 Wд1 (s) = = · 2 2 ; Mд (s) Tм s Tу s + 1 Wд2 (s) = ω2 (s) 1 1 = · 2 2 . Mд (s) Tм s Tу s + 1 и запишем их в виде, удобном для обратного преобразования 1 Wд2 (s) = γ s Wд1 (s) = · 2 Tм s + Tу2 1 · Tм s s2 + 1 Tу2 ; 1 1 Tу2 Tу2 1 + · Tм s s2 + 1 Tу2 = γ s · 2 Tм s + 1 Tу2 + Wд2 . При единичном ступенчатом воздействии на первую массу 0 при t 6 0, Mд (t) = 1 при t > 0, скорость второй массы будет равна 1 Tу2 1 ω2 (s) = Wд2 (s)Mд (s) = · Tм s s2 + 1 Tу2 + 1 s2 +a2 + 1 s2 + + Tу2 · (1 − cos Ttу ) 1 Tу2 1 a2 · (1 − cos at) = 20 1 = Tм Z ! t 1 t 1 − cos dt = t − Tу sin . Tу Tм Tу При единичном ступенчатом воздействии на первую массу, её скорость будет равна ω1 (s) = Wд1 (s)Mд (s) = γ s · Tм s2 + s s2 +a2 1 Tу2 + ω2 + s s2 + 1 Tу2 + sin at a = + Tу sin Ttу ! γTу t 1 t sin + t − Tу sin . Tм Tу Tм Tу Окончательно будем иметь выражения ω1 (t) = Tу t t + (γ − 1) sin ; Tм Tм Tу ω2 (t) = Tу t t − sin . Tм Tм Tу Из полученных выражений следует: 1. При действии на двухмассовую упругую механическую систему момента Mд в ней возникают упругие колебания с частотой ω12 = T1у , т. е. с периодом 2πTу . Поскольку система рассматривалась без учёта диссипативных сил, эти колебания не затухают. 2. Эти колебания накладываются на среднюю скорость, нарастающую при Mд = const с постоянным ускорением. q J2 3. Амплитуда колебаний второй массы при данном Mд определяется соотношением между Tу = 1c J1J1+J 2 и Tм = J1 + J2 . Амплитуда колебаний первой массы определяется значением (γ − 1)Tу /Tм . 2 Таким образом, чем больше γ = J1 +J J1 , тем больше амплитуда колебаний первой массы по сравнению с амплитудой колебаний второй. В частном случае, при γ ≈ 1, т. е. при J1 J2 колебания первой массы практически отсутствуют при наличии колебаний второй массы. При γ = 2, т. е. при J1 = J2 первая и вторая массы колеблются в противофазе с одинаковой амплитудой колебаний. В реальной механической системе колебания затухают за счёт сил трения. ω Mд 1,0 Tу Tм Tу Tм (γ − 1) ω1 0 ω2 Tм t Рис. 16. Примерный вид переходного процесса. График дорисовать Одномассовая жёсткая механическая система Хотя теоретически любая система, содержащая редуктор и муфты, обладает упругими свойствами постоянная времени упругости в силу большого коэффициента жёсткости может быть настолько мала, что учёт её при рассмотрении механической части (а затем, и всей ЭМС) не даёт практически ни какого эффекта. В этом весьма широко распространённом случае система может рассматриваться как жёсткая. Рассмотрим систему на рис. 17. После приведения моментов инерции J20 и скорости ω2 к двигателю механическую систему можно рассматривать, как единую массу с моментом инерции J = J1 + Jред + M2 = M20 /i. J20 , i2 к которой приложены моменты M1 и 21 Машина M20 ω1 M1 J1 Исполнительный орган ω2 J20 Рис. 17. Кинематическая схема. Mс Mд 1 Js ωд Рис. 18. Структурная схема одномассовой системы. В силу отсутствия упругости редуктора, в любой момент времени скорости ω1 и ω2 различаются в i раз, и всегда выполняется равенство ω1 = ω2 · i. Таким образом, момент инерции жёсткой системы равен сумме моментов инерции всех её элементов, приведённых к двигателю. Момент, действующий на исполнительный орган в одномассовой жёсткой системе, можно рассматривать, как момент, действующий непосредственно на двигатель. Обычно, для выбора электропривода её именно в таком виде и рассматривают. 22 Тема №3 Выбор электродвигателя по мощности Выбор двигателя по нагреву и перегрузочной способности для длительного и повторно-кратковременного режимов работы. Основы построения нагрузочных диаграмм электропривода. Стандартизация режимов работы. Лекция №4 Основы построения нагрузочных диаграмм изучаются самостоятально (Ковчин стр. 431, Ильинский — 487.) После того, как по технико-экономическим соображениям выбран двигатель по роду тока и принципу управления (постоянного или переменного тока, регулируемый или нерегулируемый, асинхронный, синхронный, вентильный и т. д.), его нужно выбрать по – перегрузочной способности в статическом режиме; – перегрузочной способности в динамических режимах; – по мощности. Как правило, двигатели допускают кратковременную работу с некоторой перегрузкой по моменту, характеризуемой перегрузочной сопособностью λ = Mmax /Mном . При работе в статическом режиме нагрузка на валу двигателя должна быть меньше максимально допустимого момента. Обычно считают, что перегрузка по моменту должна составлять не более 80 % от перегрузочной способности двигателя. Выбор по мощности — это выбор по допустимому нагреву. При рассмотрении нагрева двигателя делаются следующие упрощающие допущения: 1. Двигатель принимается однородным телом, обладающим бесконечно большой теплопроводностью, т. е. способностью переносить тепло от более нагретых частей тела к менее нагретым (выравнивать температуру различных частей тела). 2. Количество тепла, отдаваемое в окружающую среду, пропорционально разности температур двигателя и окружающей среды. 3. Окружающая среда обладает бесконечной теплоёмкостью, т. е. её температура не зависит от количества тепла, отдаваемого двигателем. 4. Потери в двигателе, его теплоёмкость и коэффициент теплоотдачи не зависят от температуры двигателя. При этих допущениях температура перегрева двигателя, т. е. превышение его температуры над температурой окружающей среды определяется выражением t t τ = τуст · (1 − e − Tн ) + τнач e − Tн , где τуст = ∆P A — установившаяся температура перегрева двигателя; ∆P — потери в двигателе; A — теплоотдача двигателя, измеряемая в Дж [A] = . с · ◦С Теплоотдача — это количество тепла, отдаваемое двигателем окружающей среде за одну секунду при разности температур двигателя и окружающей среды в один градус Цельсия. Tн = Ac — постоянная времени нагрева, с; c — теплоёмкость нагрева, т. е. количество тепла, необходимое для нагрева двигателя на один градус Цельсия, измеряемая в Дж/◦ С; τнач — температура перегрева в начальный момент времени, ◦ С. Стандартные режимы двигателя с точки зрения нагрева Режимы работы двигателя описаны в ГОСТ 183–74 «Машины электрические вращающиеся. Общие технические требования.» Далее рассмотрим несколько наиболее часто встречающихся номинальных режимов, на которые рассчитываются двигатели. Продолжительный режим работы (S1). Двигатель рассчитан на номинальный режим работы при номинальном токе на номинальной скорости сколь угодно долго. После начала работы двигатель успевает нагреться до установившейся температуры. Большинство двигателей выпускается для работы в режиме S1. Условие выбора двигателя при работе на постоянной скорости N 6 Nном , P, τ Pвал P, τ N = Nном P, τ 23 Pвал Tн Pmax τуст τуст ∆P ∆P 0 τ t0 T t а tр tп t ∆P б t tц в Рис. 19. Режимы работы двигателя: а — режим S1; б — режим S2; в — режим S3. где N — расчётная мощность на валу двигателя; Nном — номинальная мощность двигателя. Кратковременный режим работы (S2). Двигатель рассчитан на кратковременную работу. Под кратковременной подразумевается такая работа, при которой двигатель не успевает нагреться до установившейся температуры, а за время отключения успевает остыть до температуры окружающей среды. В дополнение к номинальным данным двигателя (напряжению, току, скорости) указывается продолжительность рабочего периода T . Повторно-кратковременный режим работы (S3). При постоянной скорости движения нагрузка носит перемежающийся характер. Циклы предполагаются одинаковыми. Работа характеризуется тем, что за время работы tр двигатель не успевает нагреться до установившейся температуры, а в период пауз tп двигатель не успевает остыть до температуры окружающей среды. Двигатель характеризуется допустимой мощностью при данной продолжительности включения ПВ%: ПВ% = tр · 100. tц Стандартными значениями ПВ являются 15, 25, 40 и 60 %. Длительность цикла не должна превышать 10 t минут. Двигатель выбирается по средней мощности Nср 6 Nном , где Nср = Nmax · tцр . Рассмотрим несколько методов расчёта двигателя для работы в режимах с переменной нагрузкой. Метод средних потерь. Если цикличность работы двигателя сохраняется, но в течение времени tр нагрузка меняется, то предварительно должны быть рассчитаны средние потери за период работы двигателя в течение цикла Pn ∆Pi ti ∆P1 t1 + ∆P2 t2 + ∆P3 t3 ∆Pср = = i=1 ; tр tр t t1 +t2 +t3 Тогда при ПВ = tцр = t1 +t надо выбрать двигатель, рассчитанный на ближайшее стандартное значение 2 +t3 +t0 ПВ, у которого номинальные потери будут равны или больше рассчитанного значения ∆Pср ∆Pном > ∆Pср . ∆P ∆P1 ∆P3 ∆Pср ∆P2 t1 t2 t3 t0 t tц Рис. 20. График мощности. К расчёту методом средних потерь. 24 Поскольку полученные значения ПВ могут значительно отличаться от расчётного, должен производиться перерасчёт расчётного режима на стандартный s ПВрасч Pстанд = Pрасч . ПВстанд Метод эквивалентного тока. Потери ∆P в электродвигателе могут быть разделены на те, которые зависят от тока ∆Pa , и те, которые от тока не зависят ∆P− . Если скорость двигателя неизменна, а меняется только его нагрузка, то потери, независящие от тока (потери вращения), можно считать постоянными. Тогда ∆P = ∆P− + ∆Pa , Если двигатель работает с постоянной скоростью, то постоянный потери ∆P− одинаковы и в рассматриваемом, и в номинальном режимах. Переменные потери ∆Pa пропорциональны квадрату тока Pn i=1 ∆Pa = ∆Pa ном · Ii 2 ti Iном tц 6 ∆Pa ном , где n — число рассматриваемых участков; ti — время работы на i-м участке; ∆Pa ном — потери в номинальном режиме; Iном — номинальный ток; tц — время цикла. Ii 2 ti i=1 Iном Pn tц 6 1; Pn 2 i=1 Ii ti 2 6 Iном ; tц sP n 2 i=1 Ii ti Iэк = 6 Iном . tц Величина, стоящая в левой части выражения называется эквивалентным током, и условием нормального теплового режима является sP n 2 i=1 Ii ti Iэк 6 Iном , где Iэк = . tц Метод эквивалентного (среднеквадратичного) момента. Для двигателей постоянного тока с независимым возбуждением использование метода вытекает из прямой пропорциональности между моментом и током Mд = cд Iя , и тогда sP Mэк = n i=1 Mi2 ti tц . Условие нормального теплового режима Mэк 6 Mном . Если скорость двигателя примерно постоянна и равна ω, то можно рассматривать фиктивную мощность, как Pэк = Mэк ω. Эта мощность должна быть меньше номинальной. Учёт пусковых и тормозных режимов. Рассмотрим теперь режим S5 (повторно-кратковременный с частыми пусками и электрическим торможением.) Если нагрузочная диаграмма содержит участки пуска, торможения и стоянки двигателя, это должно быть учтено при расчёте. v t 2 2 2 2 2 2 Mр1 tр1 + Mс1 tу1 + Mт1 tт1 + Mр2 tр2 + Mс2 tу2 + Mт2 tт2 Mэк = , tу1 + tу2 + βп (tр1 + tт1 + tр2 + tт2 ) + β0 (tп1 + tп2 ) где βп < 1 — коэффициент, учитывающий ухудшение условий охлаждения — коэффициент, учитывающий ухудшение охлаждения на стоянке. Для двигателей с вентилятором на валу . . . . . . . . . . . . . . Для закрытых, обдуваемых двигателей . . . . . . . . . . . . . . Для закрытых двигателей без обдува . . . . . . . . . . . . . . . при пуске и торможении; β0 < 1 . . . . . . . . . . . . . . . . . . β0 = 0,25 . . . 0,35; β0 = 0,30 . . . 0,55; β0 = 0,70 . . . 0,98; 25 M, n Mр1 Mс1 Mр2 Mт2 t Mс2 Mт1 tр1 tу1 tт1 tп1 tр2 tу2 tт2 tп2 tц Рис. 21. Графики скорости и момента. К расчёту методом эквивалентного момента. Для двигателей с независимым охлаждением Коэффициент . . . . . . . . . . . . . . . . . . . . . . β0 = 1. 1 + β0 . 2 Относительно сказанного выше надо сделать следующие замечания: βп = • всё относится к нерегулируемому приводу с самовентиляцией, т. е. вентилятором на валу ротора; • чтобы рассчитать нагрузочную диаграмму, надо уже выбрать двигатель, поэтому он предварительно выбирается, а затем проверяется по нагреву; • многие фирмы используют собственную ориентированную на выпускаемые двигатели методику определения мощности; • если привод регулируемый, то при ограниченном диапазоне регулирования и работе под нагрузкой на низких скоростях надо учитывать ухудшение условий охлаждения на низкой скорости, завышать установленную мощность; • при значительном диапазоне регулирования скорости должен применяться двигатель с независимой вентиляцией (когда обеспечивается принудительная подача хладагента независимо от движения вала двигателя). ГОСТ 20459–87 «Машины электрические вращающиеся. Методы охлаждения. Обозначения.» Добавить про необходимость пересчёта эквивалентного тока и момента на ПВ, по которому выбирается двигатель. ПЕРВЫЙ ТЕКУЩИЙ КОНТРОЛЬ 26 Тема №4 Электропривод постоянного тока с разомкнутой системой регулирования Физические процессы в электроприводе постоянного тока с разомкнутой системой управления. Математическое описание электропривода с двигателем постоянного тока независимого возбуждения, механические и электромеханические характеристики. Способы регулирования скорости. Динамические свойства, передаточные функции. Электропривод постоянного тока с двигателем последовательного возбуждения. Статические характеристики и способы регулирования скорости. Лекция №5 Структура электропривода постоянного тока с двигателем независимого возбуждения и разомкнутой системой управления. Естественные механическая и электромеханическая характеристики электропривода с ДПТ НВ и разомкнутой системой регулирования. Структура электропривода постоянного тока с двигателем независимого возбуждения и разомкнутой системой управления Как известно из курса электрических машин, ДПТ НВ представляет собой коллекторную машину, поток возбуждения которой создаётся отдельной обмоткой возбуждения. Которая, в свою очередь, питается от независимого источника напряжения. Двигатели постоянного тока независимого возбуждения обладают очень хорошими регулировочными свойствами, и поэтому до середины 90-х годов XX-го века являлись основным типом двигателей, использовавшихся в регулируемых приводах промышленных предприятий. В этих приводах якорная цепь двигателя питается от индивидуального регулируемого преобразователя, осуществляющего преобразование сетевого напряжения промышленной частоты (50 Гц) в напряжение постоянного тока заданной величины. Структура силовой части ЭП, которая и представляет собой ЭП с разомкнутой СУ, может быть представлена в виде рис. 22. Управление Uяз П Uя Uв ПОВ Управление Uвз Р ИО Рис. 22. Структура силовой части электропривода. На рис. обозначены: П — преобразователь в якорной цепи двигателя; ПОВ — преобразователь в цепи возбуждения; M — двигатель с обмоткой возбуждения ОВ; Р — редуктор; ИО — исполнительный орган. Якорь двигателя М и его обмотка возбуждения ОВ обычно получают питание от разных, независимых друг от друга источников (преобразователей) напряжения П и ПОВ, что позволяет отдельно регулировать напряжение на якоре двигателя и на обмотке возбуждения и выполнять их на разное номинальное напряжение. Раньше в качестве преобразователей П и ПОВ часто использовались машинные преобразователи (генераторы или ЭМУ), а в настоящее время это прежде всего тиристорные и иногда транзисторные преобразователи различных видов. Часто напряжение ОВ не регулируется, и в качестве преобразователя используется обычный диодный выпрямитель. Очевидно, что характеристики преобразоватей влияют на характеритсики ЭП. В данный момент, ради простоты, будем считать, что преобразователь в якорной цепи обладает следующими свойствами: • имеет однозначную зависимость ЭДС Eп от сигнала на входе; • характеризуется внутренним сопротивлением Rп и индуктивностью Lп ; • пропускает ток в обоих направлениях, т. е. обладает свойствами обратимости; 27 • пульсации напряжения на выходе преобразователя пренебрежимо малы. Аналогичными свойствами обладает и преобразователь ПОВ, но от него обычно не требуется свойство обратимости. Кроме того, поскольку сопротивление и индуктивность ОВ много больше внутреннего сопротивления и внутренней индуктивности преобразователя, в дальнейшем будем считать, что к ОВ приложено напряжение Uв . В отношении электрической машины будем полагать, что гистерезис в магнитной цепи и реакция якоря не проявляются, т. е. ток возбуждения iв однозначно определяет магнитный поток Φ: Φ = f (iв ) ≈ kв Iв , что щётки расположены на оси, перпендикулярной оси полюсов, и коммутация идеальна, т. е. ток переходит от одной секции обмотки якоря к другой мгновенно без каких-либо искажений; что к валу двигателя со стороны машины приложен электромагнитный момент Mэм = M, а все моменты, обусловленные механическими потерями входят в момент сопротивления Mс . С учётом всего выше изложенного можно изобразить схему замещения якорной цепи двигателя следующим образом рис. 23. Iя ∆Uяз Eп ∆Uщ Iв Eя Lв Uв Rп Rя Lп Lя Rв Рис. 23. Схема замещения системы «Преобразователь–двигатель». На рисунке обозначены Lя — индуктивность якорной цепи самого двигателя, включающая в себя индуктивности якоря, добавочных полюсов1 и компенсационной обмотки2 ; Rя — сопротивление якорной цепи двигателя (всех перечисленных обомоток); ∆Uщ — падение напряжения на щётках; Lв и Rв — индуктивность и сопротивление обмотки возбуждения. Исходя из этого схематического изображения получим уравнения для механических и электромеханических характеристик двигателя. Естественные механическая и электромеханическая характеристики электропривода с ДПТ НВ и разомкнутой системой регулирования Определение. Механической характеристикой называется зависимость частоты вращения ротора ω от электромагнитного момента M, полученная для электродвигателей в установившемся режиме работы. (предложено С. А. Ринкевичем) При этом условились складывать моменты, связанные с механическими потерями и потерями в стали электрической машины, со статическим моментом. 1 Обмотка добавочных полюсов вращающейся электрической машины — обмотка вращающейся электрической машины, расположенная на добавочных полюсах, по которой протекает ток, равный или пропорциональный току нагрузки, и которая предназначена для создания коммутирующего поля. Коммутирующее магнитное поле — это магнитное поле, индуктирующее в коммутируемой секции коллекторной машины электродвижущую силу вращения для компенсации реактивной коммутационной электродвижущей силы. Реактивная коммутационная ЭДС — это электродвижущая сила, возникающая в коммутируемой секции коллекторной машины вследствие изменения тока в ней и токов в других одновременно коммутируемых секциях, имеющих индуктивную связь с ней. Определения по ГОСТ 27471–87 «Машины электрические вращающиеся. Термины и определения.» 2 Компенсационная обмотка — обмотка вращающейся электрической машины, по которой протекает ток нагрузки или пропорциональный ему ток, расположенная таким образом, чтобы противодействовать искажению магнитного поля, вызываемому токами нагрузки, протекающими в других обмотках. Там же. 28 Определение. Электромеханической характеристикой называется зависимость скорости от тока якоря (ротора) (ω = f (I )). Определение. Коэффициентом крутизны β называется отношение β = δω/δM относительного приращения скорости δω = ∆ω/ωн к относительному приращению момента δM = ∆M/Mн 1 . В зависимости от значения величины β различают следующие четыре вида характеристик, примеры которых приведены на рис. 24: 1. Абсолютно жёсткие механические характеристики, для которых β лежит в пределах от 0 до 1 %. Такими характеристиками обладают синхронные двигатели и синхронизированные системы электропривода с машинами постоянного тока, а также шаговые двигатели, работающие в стационарном динамическом режиме. 2. Жёсткие механические характеристики, для которых β лежит в пределах от 1 до 10 %. Такими характеристиками обладают двигатели постоянного тока независимого возбуждения, некоторые коллекторные и вентильные двигатели. 3. Мякгкие механические характеристики имеют β более 10 %. К их числу относят двигатели с последовательным возбуждением, универсальные двигатели (коллекторные, включаемые непосредственно в сеть переменного или постоянного тока), асинхронные двигатели с повышенным скольжением. Мягкими являются искусственные механические характеристики многих типов двигателей. 4. Механические характеристики с переменной жёсткостью β. Например, кривая 1 рис. 24. изображает типичную механическую характеристику асинхронного двигателя с короткозамкнутым ротором. Кривая 2 — привода с «эскаваторной» характеристикой, а 3 — двигателя с последовательным возбуждением. Все характеристики на участке AB являются достаточно жёсткими, а на участке BC — мягкими. !" а) ω б) ω C 00 A 1 A0 1 2 B0 2 B 3 3 B00 C M C0 M A00 Рис. 24. Механические характеристики двигателей: а — с постоянной жёсткостью (абсолютно жёсткая 1, жёсткая 2, мягкая 3); б — с переменной жёсткостью (асинхронного двигателя 1, привода с эскаваторной характеристикой 2 и двигателя с последовательным возбуждением 3). На участках AB, A0 B0 , A00 B00 характеристика жёсткая, на участках BC, B0C 0 , B00C 00 — мягкая. Естественные механические характеристики двигатели имеют при номинальных параметрах питающей сети, нормальных схемах включения и отсутствии добавочных сопротивлений в цепях машины. Все другие механические характеристики двигателя называют искусственными. Выведем уравнения механической и электромеханической характеристик. Аналитическое выражение механической характеристики двигателя для работы в статическом режиме может быть получено из уравнения равновесия напряжений, составленного для якорной цепи схемы. При установившемся режиме работы двигателя приложенное напряжение проебразователя Eп , В, уравновешивается падением напряжения в якорной цепи Iя Rяц , падением напряжения на щётках ∆Uщ и наведенной в якоре ЭДС вращения Eя , Eп = Iя Rяц + ∆Uщ + Eя , (1) где Iя — ток в якорной цепи двигателя, A; Rяц = Rп + Rя — суммарное сопротивление якорной цепи, Ом, включающее внешнее сопротивление преобразователя Rп и внутреннее сопротивление якоря двигателя Rя (при наличии дополнительных полюсов учитывается и их сопротивление). Грубо оценить сопротивление якоря двигателя Rя можно исходя из предположения, что в номинальном режиме потери в меди ∆Pмеди составляют половину всех потерь ∆Pмеди ≈ 1 · Pном · (1 − ηном ), 2 где Pном — номинальная мощность двигателя; ηном — КПД двигателя при работе в номинальном режиме. 1 Для приводов поступательного движения, соответственно, β = δv/δF . 29 С другой стороны, 2 ∆Pмеди = Iном Rя , где Iном — номинальный ток двигателя. Откуда находим Rя = Pном (1 − ηн ) . 2 2Iном Более точные данные следует искать в каталогах или заводских формулярах на машину. Сопротивление контакта коллектор — щетки зависит от материала щеток, качества контактной поверхности и величины протекающего тока. Поэтому удобнее контактное сопротивление учитывать падением напряжения ∆Uщ , которое в зависимости от типа щёток обычно лежит в пределах от 0,3 до 3,5 В. Иногда, для простоты выкладок ∆Uщ включают в сопротивление якоря двигателя или относят к напряжению преобразователя Eп . Следует иметь в виду, что знак напряжения ∆Uщ в выражении (1) зависит от направления протекающего тока и всегда способствует его уменьшению. Т. е., когда энергия потребляется из сети (Eп Iя > 0), величина ∆Uщ в выражении (1) имеет тот же знак, что и Eп (sign ∆Uщ = sign Eп ), и напряжение, прикладываемое к коллектору машины, будет по абсолютной величине меньше на величину падения напряжения на щётках. Когда энергия поступает от двигателя в сеть (Eп Iя < 0), знак будет противоположным sign ∆Uщ = − sign Eп , и к коллектору будет прикладываться большее по абсолютной величине напряжение. Это свойство Uщ подобно свойству диссипативных моментов. Мы же для простоты дальнейших выкладок примем ∆Uщ = 0. ЭДС якоря определяется выражением Eя = cE Φω, (2) где cE — коэффициент, зависящий от конструктивных данных двигателя; Φ и ω — соответственно магнитный поток, Вб, и угловая скорость двигателя, рад/с. В системе СИ коэффициент pп N , cE = 2πa где pп — число пар полюсов двигателя; N — число активных проводников обмотки якоря; a — число пар параллельных ветвей обмотки якоря. Подставив в выражение (1) вместо Eя выражение (2), получим уравнение для скорости двигателя ω = (Eп − Iя Rяц )/cE Φ. (3) Это уравнение представляет собой зависимость скорости двигателя от тока якоря. Такую зависимость ω = f (I ) называют электромеханической характеристикой двигателя. Для получения уравнения механической характеристики необходимо найти зависимость скорости от момента двигателя. Это легко сделать, если учесть, что момент, Н · м, развиваемый двигателем, связан с током якоря и магнитным потоком простой зависимостью M = cM ΦIя . (4) Отметим, что приведенным уравнением определяется электромагнитный момент двигателя. Момент на валу двигателя будет меньше электромагнитного момента на значение, соответствующее потерям в стали и механическим потерям. Однако для практических расчетов можно пользоваться уравнениями механических характеристик, где приводится электромагнитный момент. Подставив в (3) значение тока Iя , найденное из (4), получим выражение для механической характеристики MRяц Eп ω= − , (5) cE Φ cM cE Φ2 Поскольку, в системе единиц СИ cE и cM численно равны, то можно ввести коэффициент k = cE Φ = cM Φ, с учётом которого Eп MRяц ω= − . (50 ) k k2 Коэффициент k принимается постоянным, не зависящим от нагрузки, если у двигателя с независимым возбуждением имеется компенсационная обмотка. Вообще говоря, если в двигателе нет компенсационных обмоток, устраняющих влияние реакции якоря, этот коэффициент будет переменным. В двигателях с возбуждением от постоянных магнитов реакция якоря практически не проявляется. [Онищенко стр. 105] #$ ω 30 ω ω0 II ω0 (Mном , ωном ) I II (Iя ном , ωном ) I M Iя а б Рис. 25. Механическая а и электромеханическая б характеристики. Ориентировочное значение коэффициента k можно найти по выражению k= Eян Uном − Iном Rя = , ωн ωн где Eян — ЭДС якоря в номинальном режиме, В; Uном и Iном — номинальные напряжение и ток двигателя; Rя — сопротивление якоря с учётом сопротивлений добавочных полюсов и компенсационных обомоток; ωн — номинальная скорость двигателя, рад/с. С учётом введённого коэффициента уравнение электромеханической характеристики (3) примет вид ω= Eп Iя Rяц − . k k (30 ) Механическая и электромеханическая характеристики двигателя при неизменных параметрах Eп , Φ и Rяц представляются прямыми линиями. Как указывалось выше, естественные характеристики строятсятся при напряжении преобразователя, равном номинальному напряжению двигателя, (Eп = Uном ), при номинальном потоке Φ = Φном , и отсутствии внешних добавочных сопротивлений в якорной цепи. Сопротивление преобразователя Rп также должно быть равно нулю. Расчёт и построение механической характеристики двигателя удобно выполнить по двум точкам: идеального холостого хода (ω = ω0 и M = 0 ) и номинального режима работы (ω = ωном и M = Mном ). Тогда находим Uном − ∆Uщ − Iном Rя k= , ω0 скорость идеального холостого хода (это скорость, когда электромагнитный момент равен нулю) ω0 = Uном Uном = . k cE Φном И строим характеристики Если момент нагрузки активный, то он может иметь как положительный знак, что соответствует двигательному режиму, (зона I ), так и иметь отрицательный знак, что соответствует режиму рекуперативного торможения (зона I I ). При скорости идеального холостого хода, когда ток в якорной цепи равен нулю, ЭДС якоря, направленная навстречу приложенному напряжению, равна ему по абсолютному значению. Если двигатель до приложения нагрузки работал с угловой скоростью ω0 , то при появлении на его валу момента сопротивления угловая скорость будет снижаться. Следствием этого будет уменьшение ЭДС вращения Eя , что, в свою очередь, приведёт к увеличению тока и момента двигателя. Отметим, что скорость идеального холостого хода ω0 можно получить, если все механические потери: на трение в подшипниках, щёточном аппарате и вентиляционные потери, а также потери в стали машины принять равными нулю, т. е. рассматривать идеализированный двигатель. В действительности, скорость холостого хода ωхх будет несколько ниже ω0 скорости холостого хода, и на холостом ходу двигатель будет потреблять ток холостого хода Iхх . Коэффициент крутизны механической характеристики определяется выражением " !# ω0 − ωном 1 Uном Uном Iяном Rя Iяном Rя Rя δω = = · − − = = 2. β= δM Mном Mн k k k kMн k Как было сказано выше, при увеличении нагрузки скорость машины снижается. Когда скорость снижается до нуля (ротор заторможен) двигатель работает в режиме короткого замыкания1 . При этом через 1 Режим короткого замыкания вращающегося электродвигателя — это режим работы вращающегося электродвигателя, подключенного к питающей сети при номинальном напряжении и при неподвижном роторе. 31 машину протекает ток короткого замыкания Iкз . При дальнейшем увеличении нагрузки двигатель переходит в режим противовключения. Этот тормозной режим очень тяжёлый для двигателя, т. к. в нём рассеивается как механическая энергия, поступающая с вала двигателя, так и энергия, поступающая из сети. Как было указано выше, в качестве аргумента при построении механических характеристик используют значения электромагнитного момента двигателя M. Если же использовать значение момента на валу двигателя Мд , который в двигательном режиме работы машины меньше электромагнитного момента на величину холостого хода Mхх , то в двигательном режиме он будет вычитаться из электромагнитного момента, а в тормозном будет с ним суммироваться. Таким образом, зависимость ω = f (Mд ) имеет зону нечувствительности шириной 2Mхх при изменении направления вращения якоря двигателя. Заметим, что в машинах малой мощности реакция якоря иногда не компенсируется. Поэтому, из-за продольной составляющей потока реакции якоря поток возбуждения уменьшается, и механические характеристики отклоняются от линейной зависимости (см пунктирную линию на рис. 25). Математическое описание ЭП постоянного тока с ДПТ НВ и разомкнутой системой регулирования Полученные нами выражения для механической характеристики (5) и (50 ) пригодны только для анализа электропривода в установившемся режиме работы. Составим систему уравнений привода в динамике Вначале оговорим принятые допущения 1. Размагничивающее действие якоря скомпенсировано; 2. Сопротивление и индуктивность якорной цепи постоянны1 ; 3. С механической точки зрения система представляет собой одномассовую систему с моментом инерции J = Jд + 0 Jио , i2 где i — передаточное число редуктора; Jд — момент инерции двигателя; Jио — момент инерции исполнительного органа; 4. Потери в щётках не учитываются или относятся к сопротивлению якоря двигателя; 5. Механическими потерями и потерями в стали двигателя можно пренебречь. При этих допущениях, система электропривода, в которой не производится регулирование потока, будет описываться системой уравнений dIя Eп = Eд + Iя Rяц + Lяц ; dt Eя = kω; (6) Mд = kIя ; dω 1 dt = J · (M − Mс ), где Lяц = Lя + Lп — индуктивность якорной цепи, включающая в себя общую индуктивность якоря, компенсационной обмотки и обмотки дополнительных полюсов двигателя Lя и индуктивность преобразователя Lп ; Mс — момент сопротивления на валу двигателя. Грубо индуктивность Lя можно оценить по формуле (уточнить, чья) Lя = (0,25 . . . 0,60) · Uном , Iном ωном pп где меньшая цифра относится к машинам большой мощности с компенсационной обмоткой, а бо́льшая — к нескомпенсированным машинам. d Введём оператор p = dt , и перепишем уравнения (8) в виде kя Iя = (Eп − Eд ) · (1+T ; я p) E = kω; я Mд = kIя ; 1 · (M − Mс ), ω = Jp где kя = 1/Rяц , Tя = Lяц /Rяц — коэффициент передачи и постоянная времени якорной цепи. (7) % & Eп kя Tя s + 1 Iя Eя kM 32 Mс M Mдин 1 Js ω kE Рис. 26. Структурная схема двигателя постоянного тока при постоянном потоке. Φ F Рис. 27. Примерный вид кривой намагничивания. Соответствующая структурная схема приведена на рис. 26 В более общем случае, когда ЭП включает в себя управляемые выпрямители как для якорной цепи, так и для обмотки возбуждения электрпривод будет описываться более сложной системой уравнений kя Iя = (Eп − Eд ) · ; (1 + Tя p) Eя = cE Φω; Mд = cM ΦIя ; 1 · (M − Mс ); ω= (8) Jp Uв = Iв Rв + 2pп ξwв pΦ; Φ = f (F ); F = iв wв , где Φ — поток возбуждения, Вб; Uв — напряжение на обмотке возбуждения, В; Iв — ток ОВ, А; Rв — сопротивление обмотки возбуждения, Ом; pп — число пар полюсов; ξ — коэффициент, учитывающий, что поток рассеяния сцеплен не со всеми витками обмотки возбуждения; wв — число витков обмотки возбуждения на полюс. F — намагничивающая сила, А (ампер-виток). Данное математическое описание учитывает кривую намагничивания двигателя Φ = f (F ) 1 Вообще говоря, сопротивление якоря зависит от температуры якорной обмотки, и поэтому во время работы машины меняется. Но мы этими изменениями пренебрегаем 33 Преобразуем систему к виду kя Iя = (Eп − Eд ) · ; (1 + Tя p) Eя = cE Φω; Mд = cM ΦIя ; ω = 1 · (M − M ); с Jp 1 ; Φ = (Uв − Iв Rв ) · 2pп ξw вp F = f −1 (Φ); F iв = wв , ' (9) где f −1 — функция, обратная к f . Соответствующая структурная схема ЭП приведена на рис. 28 Eп Iя kя Tя p + 1 1 2pп ξwв p Rв M cM Eя Uв Mс Mдин 1 Jp ω cE Φ Iв 1 wв F f −1 Рис. 28. Структурная схема двигателя постоянного тока при регулировании напряжением и потоком. Отметим, что регулирование скорости ДПТ НВ от нуля до номинальной скорости осуществляется изменением напряжения якоря. Регулирование скорости двигателя выше номинальной осуществляется уменьшением потока возбуждения. Реверсирование (изменение направления вращения) производится изменением полярности напряжения, подводимого к якорю двигателя или к обмотке его возбуждения. Производить реверс изменением полярности обмотки возбуждения в промышленных приводах (кроме специальных), как правило, не рекомендуется. Эта обмотка обладает значительно большей индуктивностью и поэтому процесс переключения тока возбуждения и установления нового направления магнитного потока и, следовательно, реверс двигателя будет более долгим, чем при переключении якоря. Кроме того, в момент разрыва тока в обмотке возбуждения возникает очень большая ЭДС самоиндукции, что может привести при частых переключениях к повреждению (пробою) её изоляции. добавить материал 34 Лекция №6 Механическая и электромеханическая характеристики электропривода с ДПТ НВ при введении сопротивления в цепь якоря. Механическая и электромеханическая характеристики электропривода с ДПТ НВ при изменении потока возбуждения. Механическая и электромеханическая характеристики электропривода с ДПТ НВ при изменении ЭДС преобразователя. Рекуперативное торможение электропривода с ДПТ НВ. Динамическое торможение ЭП с ДПТ НВ. ( Регулирование скорости двигателя постоянного тока независимого возбуждения может производиться тремя способами: 1. Введением добавочного сопротивления в цепь якоря. 2. Изменением величины напряжения, питающего якорную цепь двигателя, при постоянном потоке возбуждения. 3. Изменением тока возбуждения, т.е. изменением магнитного потока двигателя. Механическая и электромеханическая характеристики электропривода с ДПТ НВ при введении сопротивления в цепь якоря Рассмотрим влияние сопротивления якорной цепи на механическую характеристику. Для этого будем рассматривать схему включения двигателя, в которой в якорной цепи последовательно с якорем включён добавочный резистор Rд рис. 29. Iя Iв Eп Eя Lв Rп Rя Rв Lп Uв Lя Rд Рис. 29. Схема замещения системы «Преобразователь–двигатель» с добавочным сопротивлением. С учётом добавочного сопротивления полученные зависимости для механической и электромеханической характеристик примут вид M(Rяц + Rд ) Eп − ; ω= cE Φ cM cE Φ2 ω= Iя (Rяц + Rд ) Eп − . cE Φ cE Φ Из формул видно, что скорость ХХ определяется выражением ω= Eп cE Φ и при вводе добавочного сопротивления не меняется. А пусковой момент Mп и пусковой ток Iп (момент и ток при ω = 0) определяются выражениеми Mп = Eп · cM Φ ; Rяц + Rд Iп = Eп /(Rяц + Rд ). *) + 35 ω Rд = 0 (Естеств. хар-ка) Rд1 > 0 Rд2 > Rд1 M I 0 Рис. 30. Механические характеристики ДПТ НВ при введении сопротивления в цепь якоря. Из этих выражений видно, что при вводе добавочного сопротивления изменяется наклон механических характеристик, т.е. уменьшается их жёсткость (растёт коэффициент крутизны β1 ). Построим эти характеристики. При пуске двигателя постоянного тока независимого возбуждения прямое включение якоря в сеть, как правило, недопустимо, так как сопротивление якоря Rя незначительно и пусковой ток Iп при этом может достичь (10. . . 20)-кратного номинального значения. Это приведёт к появлению, сильного искрения — «кругового огня» на коллекторе и возможно к повреждению машины. Для сравнения, обычные ДПТ НВ допускают перегрузку по току в 2–2,5 раза от номинального тока. Включая последовательно с якорем резистор (пусковой реостат) с сопротивлением Rд , можно ограничить пусковой ток любым заданным значением Iп . По мере разгона двигателя возрастает скорость вращения якоря и его ЭДС, в связи с чем уменьшается ток. Без учета влияния ЭДС самоиндукции получим Iя = Eп − cE Φω Eп − Eя = . Rяц + Rд Rяц + Rд Вместе с уменьшением тока уменьшается и развиваемый двигателем момент и, поэтому согласно уравнению динамики уменьшается и ускорение. Для поддержания интенсивности ускорения якоря двигателя в процессе пуска необходимо уменьшать пусковое сопротивление Rд . В большинстве промышленных приводов с питанием двигателей от сети постоянного тока применяют пусковые устройства, сопротивление в которых разделено на отдельные секции (ступени) с автоматизированной системой их включения и отключения. Такой пуск двигателя с плавным или ступенчатым изменением сопротивления якорной цепи часто называют реостатным. Схема включения сопротивлений приведена на рис. 31. Eп R0 R1 R2 R0−1 R1−2 R2−3 K1 K2 K3 Rяц Рис. 31. Схема включения реостатных сопротивлений. 1 Коэффициент крутизны β был дан по учебнику Ковчина и Сабинина. Часто используется обратная величина, называемая жёсткостью. ,. Eя ω cE Φω3 ω3 cE Φω2 ω2 2 cE Φω1 ω1 1 Р. т. 36 3 0 0 Mс M I2 I1 I Рис. 32. Пусковая диаграмма при пуске ДПТ НВ. Для расчёта сопротивлений вначале выбираются максимальный пусковой ток I1 , значение которого ток якоря не дожен превышать, и минимальный пусковой ток I2 , при достижении которого должно происходить переключение на следующую ступень. Наибольшее значение тока I1 ограничивается перегрузочной способностью двигателя по току. Кроме того, ограничения могут налагаться механической частью ЭП (I1 < Mmax /cM Φ). Ток I2 выбирается исходя из статической нагрузки на валу двигателя. При этом токе электромагнитный момент должен превышать её. Рекомендуется выбирать ток I2 = (1,1 · 1,5)Iс . см. Ковчин и Сабини стр. 85. (Естественно, что в рабочей точке (Mс , ωс ) ток Iс = Mс /cM Φ, должен быть меньше Iном .) Далее, строится пусковая диаграмма, на которой наносятся, наибольший I1 и наименьший I2 токи, а также естественная и искуственные характеристики. Из пусковой диаграммы видно количество ступеней, необходимое для осуществления пуска, (в данном случае три). Рассмотрим первую ступень пуска. В исходном состоянии все ключи (K1–K3) разомкнуты. При нулевой скорости ток якоря должен быть равен I1 . Падение напряжения на якорной цепи должно равняться ЭДС преобразователя Eп . Откуда находим, что суммарное сопротивление всех последовательно включённых сопротивлений Eп R0 = . I1 Скорость, при которой должно происходить переключение на следующую ступень (в соответствии с уравнением механической характеристики) ω1 = Eп − I2 R0 . cE Φ Когда, при разгоне достигается скорость ω1 , ключ K1 замыкается, и происходит переключение на вторую ступень пуска. При этом мы переходим на следующую механическую характеристику, на которой имеет место уравнение для якорной цепи Eп = Iя · R1 + cE Φω. С учётом того, что ток якорной цепи Iя должен равняться току I1 , скорость ω будет равняться ω1 (она мгновенно измениться не может), мы получим следующее выражение для суммарного сопротивления якорной цепи R1 Eп − cE Φω1 . R1 = I1 Отсюда находим сопротивление первой ступени R0−1 = R0 − R1 , и следующую скорость переключения ω2 = Eп − I2 R1 . cE Φ 37 Аналогично на третьей ступени, когда замыкается ключ K2 мы имеем R2 = Eп − cE Φω2 ; I1 R1−2 = R1 − R2 ; ω3 = Eп − I2 R2 . cE Φ Далее нужно выйти на естетственную характеристику (замыкание K3 при замкнутых ключах K1 и K2). При ω = ω3 должно выполняться условие Eп − cE Φω3 = Rяц I1 , откуда находим R2−3 = R2 − Rяц . После замыкания ключа K3 ЭП выходит на естественную характеристику и разгоняется до установившейся скорости в рабочей точке ωс . потом доработать: вставить диаграмму, пояснить про динамический момент. Вопрос на лекции: Где на диаграмме находится динамический момент? В данных расчётах не учитывалось, что ток нарастает не мгновенно, а с замедлением, обусловленным наличием индуктивности якорной цепи. Замыкание ключей производится в функции 1. тока якоря; 2. ЭДС двигателя; 3. времени пуска на данной ступени. Каждый из этих способов имеет свои преимущества и недостатки. При замыкании ключей в функции ЭДС двигателя, (практически то же самое, что и скорости) при возникновении на валу моментов, превышающих M2 = cM ΦI2 , двигатель на рабочую скорость не выйдет, и останется на одной из промежуточных ступеней. Подобный случай возможен и при управлении ключами по току якоря. Преимуществом метода является то, что ток ни при каких условиях не превысит требуемого значения I1 . Управление по времени в отличие от предыдущих двух случаев позволяет обеспечить заданное время пуска независимо от нагрузки на валу двигателя (если, конечно она не превышает допустимых пределов). Однако, если переходный процесс в механической части на одной из ступеней затянулся, то при переключении на следующую ступень возможны броски тока, превышающие заданное значение I1 . Данный способ регулирования скорости в настоящее время во вновь проектируемых приводах практически не используется, поскольку введение добавочного сопротивления сопряжено с потерями энергии в этом сопротивлении. Механическая и электромеханическая характеристики электропривода с ДПТ НВ при изменении потока возбуждения. В большинстве случаев эти двигатели работают при номинальном потоке, значение которого находится «за коленом» кривой намагничивания стали машины. Поэтому увеличение магнитного потока выше номинального значения не практикуется, так как вследствие насыщения магнитной цепи машины существенного возрастания магнитного потока не произойдет, а значительное увеличение тока возбуждения Iв приведёт к перегреву обмотки возбуждения. Изобразить диаграмму намагничивания и показать рабочую точку. Вместе с тем ослабление магнитного потока используется достаточно часто для расширения регулировочных возможностей двигателя. (Для повышения скорости двигателя выше номинальной, для распределения момента при работе электродвигателей от общего преобразователя на общий исполнительный орган, для регулирования соотношения скоростей.) В частности, ослабление поля используется для установления основной (максимальной) скорости. В отличие от синхронных и асинхронных двигатели постоянного тока не имеют жестко определенной номинальной скорости. В каталогах указывается номинальная и максимальная скорости. Например, если указано, что двигатель мощностью 100 кВт имеет номинальную скорость 1000 об/мин и максимальную — 2000 об/мин, то основная скорость может быть установлена в этих пределах выбором соответствующего значения тока возбуждения, например, — 1600 об/мин. При этом мощность двигателя останется равной 100 кВт. Онищенко /0 ω ω ω02 ω02 ω01 ω01 ω0 ω0 0 Mкз2 Mкз1 Mкз M а Iкз 0 38 I б Рис. 33. Механическая а и электромеханическая б характеристики при ослаблении потока ДПТ НВ. При ослаблении потока зависимости для механической и электромеханической характеристик примут вид MRяц Eп − ; ω= cE Φ cM cE Φ2 ω= Iя Rяц Eп − . cE Φ cE Φ Из формул видно, что скорость ХХ, определяемая выражением ω= Eп , cE Φ при ослаблении потока будет расти. Ток короткого замыкания Iкз = Eп /Rяц , останется неизменным, т. к. от потока не зависит, а зависит только от ЭДС преобразователя. Пусковой момент Mп будет уменьшаться Eп · cM Φ Mп = = Iкз cM Φ. Rяц Как видно из графиков, жёсткость механических характеристик при ослаблении поля уменьшается. Как видно из рис. любые две механические характеристики имеют точку пересечения. При значениях статического момента, расположенных левее точки пересечения, ослабление магнитного потока приводит к увеличению скорости двигателя. Если же значение момента нагрузки расположено правее точки пересечения, то ослабление магнитного потока приводит к падению скорости двигателя — это явление называют «опрокидыванием регулирования». Причем, чем больше ослабляется магнитный поток машины, тем при меньших значениях нагрузки наступает опрокидывание регулирования. Для двигателей нормального исполнения точки пересечения механических характеристик обычно лежат в зоне очень больших токов, недопустимых по условиям коммутации. Однако, это выполняется не всегда. При анализе механических характеристик при ослаблении поля следует иметь в виду, что при работе с постоянным статическим моментом ток якоря по мере ослабления потока увеличивается. Так, если статический момент на валу двигателя будет равен номинальному, то при номинальном напряжении якоря двигатель будет работать в т. 1. Если, например, ослабить поток возбуждения в два раза, то скорость холостого хода двигателя увеличивается в два раза. Если момент двигателя сохранится постоянным и равным номинальному, то двигатель будет работать в т. 2. Однако, как это следует из выражения для электромеханической характеристики, ток якоря при этом увеличится в два раза. Поэтому длительная работа двигателя в т. 2 недопустима. Из этого примера следует, что одновременно с повышением скорости необходимо снижать длительно допустимый по условия нагрева (номинальный) момент. Линия номинального момента при ослаблении поля будет иметь вид показать гиперболу . Аналогично при ослаблении поля уменьшается допустимый максимальный момент, определяемый по условиям коммутации на коллекторе. Поскольку при ослаблении поля скорость увеличивается примерно пропорционально степени ослабления поля Φ/Φном длительно допустимый момент уменьшается пропорционально этому же отношению Φ/Φном , то длительно допустимая мощность двигателя N = Mω остается примерно постоянной. Поэтому регулирование ослаблением поля называют регулированием с постоянной мощностью в отличие от регулирования изменением напряжения якоря при постоянном потоке возбуждения, которое называют регулированием с постоянным моментом. 12 ω 39 ω M 0 Iя 0 а б Рис. 34. Механическая а и электромеханическая б характеристики ДПТ при регулировании ЭДС преобразователя. Вообще одного и того же значения скорости и одного и того же значения момента можно достичь разными комбинациями значений потока возбуждения и ЭДС преобразователя. Но минимум потерь в двигателе всегда будет достигаться при наибольшем потоке возбуждения. Управление током возбуждения требует менее мощного преобразователя, чем регулирование напряжения в якорной цепи. Но из-за того, что индуктивность обмотки возбуждения значительно превышает индуктивность якорной цепи, регулирование скорости будет менее быстродействующим. Поэтому его можно использовать в тех случаях, когда нужно регулировать скорость в небольших пределах от установовившегося значения, и когда не предъявляется высоких требований к динамике. Механическая и электромеханическая характеристики электропривода с ДПТ НВ при изменении ЭДС преобразователя. Основным способом регулирования скорости двигателей постоянного тока независимого возбуждения (ДПТ-НВ) является регулирование напряжения Eп , подводимого к якорю двигателя. Изменение скорости при этом производится вниз от основной (номинальной) скорости, определяемой естественной характеристикой. Из выражений для механической и электромеханической характеристик видно, что при изменении ЭДС они будут представлять собой семейство прямых параллельных линий ω= MRяц Eп − ; cE Φ cM cE Φ2 ω= Iя Rяц Eп − . cE Φ cE Φ При уменьшении напряжения якоря уменьшается скорость холостого хода ω0 , а жесткость механических характеристик остается постоянной. Повышение напряжения питания выше номинального не рекомендуется, т.к. это может ухудшить коммутацию на коллекторе. Первый и третий квадранты являются двигательными, а второй и четвёртый — тормозными. На рис. линия, проходящая через центр координат соответствует динамическому торможению, когда знергия рассеивается на сопротивлении преобразователя и якорной цепи двигателя. Она не проходит через двигательные квадранты и поэтому в статическом режиме может иметь место только при наличии активных моментов сопротивления. Участки механических характеристик во втором квадранте, лежащие выше линии динамического торможения соответствуют области рекуперативного торможения, а лежащие ниже — области торможения противовключением. Участки линии в третьем квадранте соответствуют двигательному режиму, когда вал двигателя вращается в противоположную сторону. Аналогично линии в четвёртом квадранте, лежащие ниже линии динамического торможения, соответствуют рекуперативному режиму работы. Плавность регулирования, отсутствие дополнительных потерь энергии при регулировании и высокая жесткость механических характеристик составляют основные достоинства этого способа регулирования скорости. Кроме того, ввиду малой индуктивности обмотки якоря, данный способ обеспечивает более высокое быстродействие, чем регулирование током возбуждения. Как видно из механических характеристик, всего существует три способа торможения электропривода 1) торможение с отдачей энергии в сеть (рекуперативное); 2) динамическое торможение; 3) торможение противовключением. 40 Каждый тормозной режим является генераторным, так как энергия поступает в машину с вала, преобразуется в электрическую и либо отдается в сеть, либо затрачивается на нагрев элементов якорной цепи, обладающих активным сопротивлением, и рассеивается в окружающую среду. Рассмотрим подробнее особенности механических характеристик при указанных способах торможения. Рекуперативное торможение электропривода с ДПТ НВ. В этом режиме якорь двигателя приводится во вращение моментом механизма со скоростью, превосходящей скорость идеального холостого хода. Рассмотрим пример рис. 35. M ω РД Т Eп ω1 Б Г v F 45 Рис. 35. Пример кинематической схемы механизма, работающего в режиме рекуперативном торможения. На рисунке изображены двигатель M, который приводит через редуктор РД во вращение барабан Б. На барабан навит трос, который поднимает и опускает груз Г. В исходном состоянии груз удерживается томозом Т. В начальный момент времени растормаживается тормоз Т, и подаётся питание на двигатель M, причём таким образом, что создаваемый при пуске момент, совпадает по направлению с моментом, создаваемым грузом. По мере увеличения скорости двигателя, его электромагнитный момент уменьшается в соответствии с уравнением механической характеристики, и когда скорость достигнет скорости идеального холостого хода электромагнитный момент станет равен нулю. Но поскольку на валу двигателя будет присутствовать крутящий момент, создаваемый силой тяжестью F , то скорость ротора будет и дальше расти. Когда она привысит значение идеального холостого хода, момент на валу двигателя станет направлен против скорости вращения вала, и по мере роста скорости будет возрастать. Двигатель войдёт в рекуперативный режим. Когда момент на валу двигателя сравняется с моментом, создаваемым силой тяжести, ускорение вала прекратится, и начнётся статический режим работы. При работе со скоростью выше скорости идеального холостого хода ЭДС якоря Eя становится больше ЭДС преобразователя Eп , что приводит к изменению направления тока якоря Iя и электромагнитного момента M. При этом, двигатель становится источником электроэнергии, а преобразователь — её потребителем. Рассмотрим ещё один важный пример, как осуществляется переход в режим рекуперативного торможения при снижении ЭДС преобразователя Eп . ω Mс ω Mп 0 а M Mс 0 M б Рис. 36. Переход в режим рекуперативного торможения при активном моменте нагрузки а и пассивном моменте б. 41 Пусть к валу двигателя приложен статический момент Mс . Электромагнитный момент двигателя M > 0 уравновешивает его. К якорю двигателя приложена ЭДС преобразователя Eп1 , и двигатель работает на механической характеристике 1, в рабочей точке A со скоростью ω1 . В какой-то момент времени ЭДС преобразователя скачком уменьшается до значения Eп2 < Eп1 . При этом, ЭД переходит на новую механическую характеристику 2. Поскольку, в силу инерционности ротора двигателя и приводного механизма скорость двигателя ω скачком измениться не может и в момент перехода сохраняется равной ω1 , то рабочая точка A скачком переходит в точку B, соответствующую рекуперативному режиму торможения. К валу двигателя прикладывается динамический момент Mдин = MB − Mс , равный сумме момента двигателя в точке B и момента сопротивления. Таким образом, момент двигателя и момент сопротивления начинают действовать в одну сторону. Под действием динамического момента ротор начинает замедляться, и точка B плавно переходит C по механической характеритике. По мере снижения скорости ω, ЭДС двигателя Eя снижается, и как следствие, снижается ток якоря Iя = Eп − cE Φω . Rяц Это ведёт к снижению абсолютной величины электромагнитного момента двигателя. После того, как скорость станет ниже скорости идеального холостого хода характеристики 2, двигатель перейдёт в двигательный режим, а ток и момент двигателя начнут возрастать. Теперь уже электромагнитный момент двигателя будет действовать против момента сопротивления. Электромагнитный момент будет возрастать до тех пор, пока не уравновесит момент сопротивления в точке C. После этого переходный процесс закончится, и вал двигателя будет вращаться с новой скоростью ω2 . Рекуперативное торможение является весьма экономичным, поскольку оно сопровождается отдачей в сеть электрической энергии (за вычетом потерь в двигателе), которую двигатель преобразует из механической, поступающей к нему с вала. Но торможение этим способом может быть осуществлено в ограниченных пределах, так как не всегда можно обеспечить, чтобы скорость привода ω превышала скорость идеального холостого хода. На низких оборотах это вообще не возможно, т. к. стоящий при моменте в механической характеристике коэффициент cERcMяцΦ2 нельзя делать сколь угодно малым. Поэтому для полной остановки привода приходится переходить на другие тормозные характеристики, или прибегать к торможению электромеханическим тормозом (наложению колодок). К достоинствам рекуперативного торможения относится высокая жесткость механических характеристик; плавный переход из двигательного в тормозной режим на одной и той же характеристике. Благодаря такому характеру механических характеристик улучшается качество управления приводом. Динамическое торможение ЭП с ДПТ НВ. В режиме электродинамического (динамического) торможения якорная цепь двигателя замыкается на внешний тормозной резистор Rтр рис. 37 , а обмотка независимого возбуждения ОВ остается включенной в сеть, чтобы сохранить магнитный поток. Поскольку якорь двигателя отключается от сети, но сохраняет прежние направления вращения и ЭДС, ток в якоре (момент) изменяет направление и становится тормозным Iт = − cE Φω . Rяц + Rтр При этом, так же как и в случае рекуперативного торможения, механическая энергия, поступающая с вала, например, в виде кинетической энергии, запасенной в двигателе и в движущихся элементах приводимого им механизма, преобразуется в электрическую. Однако эта энергия не отдается в сеть, а расходуется на нагрев сопротивления Rтр и обмоток цепи якоря двигателя. Поэтому такое торможение является диссипативным, в отличие от рекуперативного. Уравнение механической характеристики для этого режима получается подстановкой Eп = 0 в общее выражение механической характеристики ω=− Rяц + Rтр · M. cE cM Φ2 ω=− Rяц + Rтр · M, k2 или при постоянном потоке Φ где k = cE Φ = cM Φ. Как видно из приведённых формул при различных значениях тормозного сопротивления характеристики будут представлять собой пучок прямых с центром в начале координат, расположенных во втором и четвертом квадрантах. При увеличении тормозного сопротивления жёсткость характеристик будет уменьшаться. Тормозное действие динамического торможения ослабляется по мере снижения скорости вращения. Для его 67 42 ω Uв M M 0 Rтр а б Рис. 37. Схема включения а и механические характеристики б ДПТ НВ при динамическом торможении. поддержания можно переходить на новые механические характеристики, уменьшая тормозное сопротивление Rтр или закоротив якорь. При отсутствии возбуждения динамическое торможение невозможно. Вопрос. Изменением ещё каких параметров можно повлиять нажёсткость механической характеристики? Рассмотреть вопрос спуска груза и действия при статическом моменте Различие режимов динамического торможения при реактивном и активном статических моментах состоит c том, что в первом случае процесс торможения совершается до полной остановки привода, а во втором — только до скорости установившегося движения ω0 . Поэтому для достижения полной остановки механизма в конце электродинамического торможения переходят на механическое торможение, для которого используется специальное тормозное устройство. Недостатками режима динамического торможения являются: потери энергии торможения, расходуемой на нагрев элементов привода, и невозможность торможения привода до полной его остановки при наличии активного момента на его валу. Достоинством режима динамического торможения является его высокая надежность, определяемая тем, что этот режим может осуществляться при выходе из строя источника питания цепи якоря, когда режим рекуперативного торможения становится невозможен. Исходя из этого, динамическое торможение в приводах постоянного тока часто используется в качестве средства аварийного торможения. Динамическое торможение широко используется для останова привода при отключениях его от сети (особенно при реактивном характере момента), при спуске грузов в подъемных механизмах. 8 43 ω Φ < Φном Rя > Rяц M 0 Eп < Eп ном Rяц + Rтр Рис. 38. Переход ДПТ в режим противовключения. Лекция №7 Режим противоточного торможения ЭП с ДПТ НВ. Реверс ЭП с ДПТ НВ при активном моменте нагрузки. Реверс ЭП с ДПТ НВ при пассивном моменте нагрузки. Способы ограничения тока при пуске ЭП с разомкнутой системой регулирования и ДПТ НВ. Двухзонное регулирование скорости. Работа ЭП с ДПТ НВ в системе генератор-двигатель. Режим противоточного торможения ЭП с ДПТ НВ. (Торможение противовключением.) Противовключением называют режим, при котором якорь двигателя вращается под действием активных моментов или моментов, определяемых запасом кинетической энергии, в противоположном направлении, по сравнению с направлением, которое было бы у двигателя на холостом ходу1 Возможны две разновидности торможения. Первая — торможение изменением направления тока якоря и электромагнитного момента за счёт переключения полярности подводимого к якорю напряжения. Моменты, развиваемые двигателем и рабочим механизмом, действуют в одном направлении, обратном направлению вращения якоря, скорость которого снижается до нуля и затем может изменить свое направление на обратное, если двигатель не отключить от сети при скорости, равной нулю. Нарисовать картинку. Следует отметить, что если на якоре просто изменить полярность напряжения, то через якорь могут течь очень большие токи. Кроме того, после остановки двигатель начнёт раскручиваться в обратную сторону. Для уменьшения тока в якорную цепь последовательно с двигателем включают тормозные сопротивления Rтр . Нарисовать мех. хар-ку, задать вопрос. Если сопротивление Rтр достаточно велико, то, достигнув нулевой скорости, двигатель останавливается, поскольку реактивный статический момент, меняя свой знак, препятствует вращению привода в противоположную сторону. Такая разновидность торможения применяется в механизмах с реактивным статическим моментом, изменяющим свое направление вместе со скоростью, если необходима его быстрая остановка. Показать динамический момент Если режим противовключения осуществляется с меньшим сопротивлением Rтр , то после достижения нулевой скорости двигатель может совершить реверс и перейти из тормозного режима противовключения в двигательный режим работы с установившейся скоростью ωс1 . Для исключения реверса привода при достижении нулевой скорости двигатель отключают от сети и осуществляют механическое торможение. Вторая разновидность торможения — вращением якоря в направлении момента рабочего механизма с противодействующим электромагнитным моментом. Нарисовать картинку При наличии активного статического момента, например в крановых установках, режим противовключения получают без переключения полярности на якоре двигателя, лишь введением большого сопротивления Rтр в цепь якоря. Тогда под действием активных моментов якорь двигателя затормаживается, а затем начинает вращаться в противоположном направлении, и ЭДС меняет свой знак. Ток (момент) двигателя при работе его в четвертом квадранте, сохраняет прежнее направление. Показать динамический момент Очевидно, в этом случае возможно обеспечить тормозной режим с различными скоростями ω < 0, в том числе и полную остановку привода, что определяется величиной сопротивления Rтр . 1 Это определение несколько отличается от приводимого в ГОСТ 27471, где торможением противовключением называется электрическое торможение вращающегося электродвигателя, осуществляемое путём переключения его обмоток в положение, соответствующее другому направлению вращения. Данное определение по ГОСТ не учитывает режим торможения противовключением, которое можно получить введением добавочных сопротивлений без переключения его обмоток. 44 Работа привода при скорости ω < 0 применяемая в подъёмно-транспортных установках, называется силовым спуском груза. Заметим, что при одной и той же величине активного и пассивного моментов, при введении в цепь якоря сопротивления Rтр , процесс достижения нулевой скорости при наличии пассивного момента будет происходить значительно быстрее, чем при наличии активного момента. Это объясняется тем, что при работе привода в первом квадранте динамический момент, а следовательно, и замедление определяются не суммой моментов, а их разностью. В отличие от рекуперативного торможения, когда энергия поступает от механизма в двигатель и затем отдаётся в сеть, в режиме противовключения, в двигатель не только поступает энергия от механизма, но так же поступает и от сети. Режим противовключения обеспечивает интенсивное торможение привода до полной остановки, но сопровождается значительным потреблением энергии от сети и существенным нагревом обмоток двигателя и тормозных сопротивлений при её рассеивании. В режим противоточного торможения также можно попасть при сильном ослаблении потока Φ или при сильном снижении ЭДС преобразователя. Реверс ЭП с ДПТ НВ при пассивном моменте нагрузки. Реверс ЭП с ДПТ НВ при пассивном моменте нагрузки возможно осуществить переключением зажимов якорной цепи, при этом должно быть предусмотрено ограничение тока якоря. Направление тока в подмагничивающей сериесной обмотке должно оставаться неизменным, т. к. поток направления не меняет, а сериесная (!!!) обмотка должна оставаться подмагничивающей. В точке A в исходном состоянии включены контакты В и отключены контакты Н. Сопротивления якоря шунтируются контакторами. Ток якоря 9 Iя = Iс = Eп − cE Φω1 . Rяц Для начала реверса отключаются контакты В и включаются контакты Н. Кроме того, включаются добавочные сопротивления в цепь якоря (все). При этом электропривод скачком переходит в точку B. В первый момент скорость равна ω1 . Ток якоря Iя max = −Eп − cE Φω1 . Rяц + Rдоб Если у нас I1 — пусковой ток, который поддерживается при пуске привода сопротивлениями R0−1 . . . R2−3 , то чтобы при торможении (при переходе из точки B в точку C) тормозной ток не превышал пускового, необходимо, чтобы тормозное сопротивление RТ , было примерно равно сумме сопротивлений R0−1 . . . R2−3 . Это объясняется тем, что при переключении полярности к сопротивлениям прикладывается практически двойное напряжение |Eп | + |Eя | (|Eп | ≈ |Eя |). В Н K1 K2 K3 KТ R0−1 R1−2 R2−3 RТ Пусковые сопротивления Н В Тормозное сопротивление Рис. 39. Схема реверсирования электропривода с ДПТ НВ. Режим реверса состоит из двух этапов. 1. Торможение противовключением, поскольку после переключения напряжения на зажимах двигателя ЭДС двигателя и напряжение действуют в одном направлении. 2. Разгон в противоположную сторону, который осуществляется также, как и пуск. : ;<= 45 ω A B −I2 C −I1 0 I Iс −Iс D Рис. 40. Механические характеристики при реверсе электропривода с ДПТ НВ. Если в точке C снять напряжение с двигателя, он остановится. Реверс ЭП с ДПТ НВ при активном моменте нагрузки. Исходно находимся в точке A рис 41. В момент начала реверса скачком переходим в точку B. В результате снижения момента двигателя возникает динамический момент, который вначале затормаживает двигатель, а затем переводит его в режим противовключения. ω A B ω ω M 0 C v v Рис. 41. Динамическое торможение при активном моменте нагрузки введением добавочного сопротивления в цепь якоря. В отличие от предыдущего случая при реверсе с пассивным моментом, при активном моменте режим противовключения возникает не в результате изменения полярности напряжения преобразователя Eп , а из-за изменения знака ЭДС двигателя, вызванного изменением вращения ротора двигателя. Требуемое значение сопротивления Rдоб может быть определено из равенства Eп − cE Φω1 Eп + cE Φ|ω2 | = . Rяц Rяц + Rдоб Двухзонное регулирование скорости. Для электроприводов многих механизмов используют комбинированное управление, так называемое двухзонное регулирование скорости. Механические характеристики для этого способа привести. В первой зоне скорость двигателя в диапазоне от нуля до основной скорости регулируется изменением напряжения 46 преобразователя Eп при постоянном потоке возбуждения Φном . Во второй зоне регулирование производится изменением тока (потока) возбуждения при постоянном номинальном напряжении якоря. Для этой цели в настоящее время используются нереверсивные управляемые выпрямители, включаемые в цепь возбуждения. Соответственно номинальный момент в первой зоне регулирования остается постоянным, а во второй зоне снижается пропорционально уменьшению потока. Максимально допустимая скорость двигателя при ослаблении поля определяется механической прочностью якоря и условиями коммутации на коллекторе. Эта скорость указывается в каталоге на двигатели. Как мы ранее рассматривали, при работе во второй зоне (зоне ослабления потока), чтобы двигатель не перегревался, необходимо поддерживать ток не выше номинального, что приводит к снижению номинального момента Mн = cM ΦIя ном . Момент снижается прямо пропорционально уменьшению потока Φ/Φном . При этом, скорость будет возрастать ωн = MRяц Eп ном − Iя ном Rяц Eп ном Iя ном Rяц Eп ном = − − = . cE Φ cE Φ cM Φ cM Φ cE cM Φ2 обратно пропорционально ослаблению потока Φ/Φном . Механическая мощность при ослаблении поля N = ωM = Eп ном − Iя ном Rяц · cM ΦIя ном = (Eп ном − Iя ном Rяц ) · Iя ном , cM Φ остаётся постоянной. При регулировании в первой зоне поток равен номинальному, соответственно момент при изменении ЭДС преобразователя не изменяется Mн = cE Φном Iя ном . А скорость при увеличении ЭДС преобразователя линейно растёт Eп − Iя ном Rяц MRяц Eп = − . ω= 2 cE Φном cE cM Φном cM Φном Номинальная механическая мощность при увеличении ЭДС N = ωM = Eп − Iя ном Rяц · cM Φном Iя ном = (Eп − Iя ном Rяц ) · Iя ном = Eп Iя ном − Iя2ном Rяц , cM Φном также линейно растёт. Нарисовать графики момента и мощности. Следует отметить, что графики номинального момента и номинальной мощности показывают верхнюю границу длительно допустимого момента и верхнюю границу длительно допустимой мощности. Реальные момент и мощность могут быть и меньше. Максимально допустимый ток якоря ДПТ ограничен условиями коммутации на коллекторе, поэтому при ослаблении поля максимально допустимый момент также будет уменьшаться, (чтобы ток не превышал максимально допустимых величин). Работа ЭП с ДПТ НВ в системе генератор-двигатель. Схема системы генератор-двигатель (Г–Д) приведена на рис. 42. На схеме обозначены АД — асинхронный двигатель; Г — генератор с обмоткой возбуждения ОВГ; Д — двигатель с обмоткой возбуждения ОВД; В — возбудитель с обмоткой возбуждения ОВВ. Вместо электромашинного возбудителя, приведённого на этой схеме, может использоваться статический возбудитель (управляемый или неуправляемый выпрямитель). Скорость вращения регулируется здесь в общем случае двумя способами — изменением напряжения, подводимого к двигателю при его номинальном токе возбуждения, и изменением потока двигателя при постоянном напряжении якоря. В первом случае регулирование возможно при неизменном моменте, если допускается постоянство величины тока, M = cM Iя Φ. По той же причине во втором случае регулирование можно принять при постоянной мощности Pэ = Eп Iя с моментом, обратно пропорциональным скорости вращения M = Pωэ . При пуске системы Г–Д вначале пускается приводной асинхронный двигатель АД. При этом генератор Г не должен быть возбужден, а двигатель Д получает полное возбуждение от возбудителя В. Увеличивая ток возбуждения генератора, увеличивают его ЭДС Eп . Уравнение механической характеристики системы Г–Д будет иметь вид ω= Rяц M Eп − , cE Φд cE cM Φ2д где Eп — ЭДС генератора; cE , cM — конструктивные постоянные двигателя; Φд — поток двигателя; Rяц — суммарное сопротивление якорной цепи. При номинальном потоке двигателя регулирование скорости производится изменением потока генератора Φг , т. е. ЭДС генератора. При достижении номинального значения ЭДС генератора дальнейшее повышение его тока возбуждения нецелесообразно, так как магнитная система генератора насыщается и это не приводит к заметному возрастанию ЭДС машины. Увеличить скорость можно, ослабляя магнитный поток 47 ВСТАВИТЬ РИСУНОК ACAD19! Рис. 42. Электрическая схема системы генератор-двигатель. двигателя, при этом механические характеристики системы Г–Д имеют такой же вид, как и у двигателя независимого возбуждения, получающего питание от сети при ослаблении магнитного потока. Различие состоит лишь в том, что в системе Г–Д будет бо́льшим сопротивление якорной цепи Rяц , и, соответственно, механическая характеристика будет мягче. Первый поддиапазон регулирования скорости при изменении потока генератора и постоянном потоке двигателя, равном номинальному, характеризуется параллельностью механических характеристик и при постоянном токе в якорной цепи соответствует режиму регулирования скорости с постоянным моментом. При ослаблении магнитного потока двигателя и постоянном, равном номинальному, потоке генератора получаем режим регулирования скорости с постояиной мощностью. При этом жёсткость механических характеристик будет уменьшаться. Основной тормозной режим системы Г–Д — генераторный с отдачей энергии в сеть. При работе привода с угловой скоростью, превышающей номинальную скорость холостого хода вначале увеличивают ток возбуждения двигателя, при этом его ЭДС становится больше значения напряжения на зажимах генератора. Машины меняются ролями: двигатель превращается в генератор, обеспечивая тормозной момент, а генератор становится двигателем и через асинхронную машину, работающую в генераторном режиме, отдаёт энергию в сеть. Затем, когда скорость становится ниже скорости ХХ на новой характеристики, все машины возвращаются в свои основные режимы работы до последующего увеличения тока возбуждения двигателя. Изобразить на механической характеристике процесс торможения. После того как исчерпаны возможности торможения увеличением тока возбуждения двигателя, начинают уменьшать ток возбуждения генератора. Это также приводит к уменьшению напряжения на его якоре и дальнейшему получению тормозных режимов, но уже при угловой скорости привода меньшей номинального значения. При нулевом токе возбуждения генератора его остаточное напряжение может создать, в якорной цепи такой ток, который может быть достаточен для преодоления статического момента и вращения механизма с небольшой «ползучей» скоростью ωп . Для исключения такого неуправляемого режима работы привода обычно обмотку возбуждения генератора при остановке системы подключают к зажимам якоря так, чтобы в ней протекал ток, размагничивающий генератор. > 48 ω Φг = const, Φд = var Естетственная характеристика ω0 Φг = var, Φд = const 0 M Рис. 43. Семейство механических характеристик при регулировании скорости в системе генератор–двигатель. Системы Г–Д без обратных связей позволяют получать диапазон регулирования 1 : 20 . . . 1 : 30. Данное ограничение пределов регулирования обусловлено значительной величиной падения напряжения в щёточных контактах и обмотках якорей по сравнению с ЭДС генератора при малых его токах возбуждения, а также наличием остаточной магнитной индукции в генераторе. В замкнутых системах управления с отрицательными обратными связями диапазон регулирования составлял 1 : 2000. Недостатком системы Г–Д являются увеличение установленной мощности (в три раза), снижение КПД установки вследствие трёхкратного основного преобразования энергии, а следовательно, большого увеличения затрат на оборудование и эксплуатацию установки. Система генератор-двигатель, в которой двигатель постоянного тока получает питание от электромашинного агрегата, в настоящее время морально устарела и в стационарных установках не применяется. Система Г–Д продолжает использоваться для мобильных установок, например экскаваторов. 49 Лекция №8 Структура якорной цепи ЭП с ДПТ НВ и условия ограничения тока. Структура якорной цепи ЭП с ДПТ НВ и условия ограничения тока. Вернёмся к структурной схеме ДПТ НВ с постоянным потоком возбуждения. Динамика привода описывается системой дифференциальных уравнений Eп = kω + Rяц · Iя + Lяц pIя , kIя − Mс = Jpω. Назвать переменные В этих уравнениях kω — ЭДС якоря; kIя — электромагнитный момент двигателя. ! Rяц Eп kω pIя = − − Iя , Lяц Rяц ! Rяц k Mс pω = J Iя − k . В отличие от полной структурной схемы, учитывающей возможность регулирования потока возбуждения, данная схема линейна (поток Φ = const, и электрическая машина скомпенсирована). Выходными координатами являются ток якоря Iя (или пропорциональный ему момент двигателя) и скорость ω, которые меняются под действием внешних воздействий: управляющего — ЭДС преобразователя Eп , и возмущающего — Mс . Обозначим Tя = Lяц /Rяц — постоянная времени якорной цепи. ! kω 1 Eп − − I , pI = я я Tя Rяц !Rяц (10) k Mс I − . pω = я J k Продифференцируем первое уравнение и подставим в него вместо pω второе. p 2 Iя = pEп pIя k2 Iя kMс − + − . RяцTя Tя JRяц Tя JRяц Tя Обозначим электромеханическую постоянную времени Tэм = JRя . k2 (11) p 2 Iя = pEп pIя Iя Mс − − + . RяцTя TяTэм TяTэм k Tя p2 Iя + pIя pEп Iя Mс . + = + Tя TяTэм RяцTя TяTэм k TэмTя p2 Iя + Tэм pIя + Iя = Tэм pEп Mс + . Rяц k (TэмTя p2 + Tэм p + 1) · Iя = Tэм pEп Mс + . Rяц k Вынесем ток якоря за скобки Обозначим F (p) = TэмTя p2 + Tэм p + 1. Найдём теперь передаточные функции тока якоря Iя и скорости ω по ЭДС преобразователя, для чего примем момент механизма Mс = 0. F (p) · Iя = Tэм pEп ; Rяц Откуда передаточная функция тока якоря по ЭДС преобразователя p Iя Tэм = · . Eп Rяц F (p) Подставим выражение для тока во второе уравнение системы (10) с учётом того, что Mс = 0 pω = p k Tэм · · · Eп . J Rяц F (p) (12) 50 ω k 1 = · Tэм · . Eп JRяц F (p) Откуда с учётом (11) получим передаточную функцию скорости якоря по ЭДС преобразователя 1 ω = . Eп kF (p) (13) Теперь найдём передаточные функции по моменту сопротивления, для чего примем ЭДС преобразователя равной нулю. Тогда Mс F (p) · Iя = , k или Iя 1 = . (14) Mс kF (p) Подставим выражение для тока во второе уравнение системы (10). ! Mс k Mс − ; pω = J kF (p) k p ω 1 1 − F (p) 1 1 − TэмTя p2 − Tэм p − 1 −Tэм Tя p2 + p = · = · = · ; Mс J F (p) J F (p) J F (p) −Tэм Tя p + 1 ω · , = Mс J F (p) или с учётом (11) ω Rя Tя p + 1 =− 2 · . Mс F (p) k (15) Задание. Получить передаточные функции методом структурных преобразований из схемы электропривода рис. 26. Оцененим установившиеся значения. Как известно, значение оригинала f (t) при t → ∞, равно значению изображения F (p) при p → 0. Поэтому, в полученных передаточных функциях положим нулю переменную p. Очевидно, что F (p)|p=0 = TэмTя p2 + Tэм p + 1|p=0 = 1. Тогда Iя Eп = p=0 p Tэм · Rяц F (p) = 0. p=0 Из этого выражения видно, что вклад изменения ЭДС преобразователя Eп в изменение установившегося значения тока якоря будет равно нулю. Это объясняется тем, что момент нагрузки непосредственно от ЭДС преобразователя не зависит поэтому и ток меняться не будет. ω Eп = p=0 1 kF (p) = p=0 1 . k Из этого выражения видно, что если момент сопротивления не изменяется, то при изменении Eп скорость изменится ровно на столько, насколько изменится скорость холостого хода. Это выражается в параллельном перемещении механических характеристик. Iя Mс = p=0 1 kF (p) = p=0 1 . k Из этого выражения видно, что насколько изменяется момент нагрузки, настолько изменяется и установившееся значение момента двигателя M = Iя k. Также видно, что при изменении Eп скорость двигателя изменяется также, как и ток якоря при изменении, момента нагрузки. ω Mс =− p=0 Rя Tя p + 1 · F (p) k2 =− p=0 Rя . k2 Здесь видно, что при увеличении нагрузки, скорость уменьшается (знак «минус»), величина изменения определяется жёсткостью характеристики. 51 Далее, на основе полученных передаточных функций (12)–(15) рассмотрим как будет вести себя двигатель в динамике на примере передаточной функции скорости двигателя по ЭДС преобарзователя ω 1 = . Eп kF (p) Очевидно, что динамика будет определяться соотношением корней полинома F (p). Приравняем его нулю, TэмTя p2 + Tэм p + 1 = 0; и найдём корни квадратного уравнения p1,2 = −Tэм ± q 2 Tэм − 4TяTэм 2TяTэм , Очевидно, что, если подкоренное выражение положительно, т. е. Tэм > 4Tя , то корни уравнения будут действительными числами, а если отрицательно (Tэм < 4Tя ), то корни будут комплексно-сопряжёнными числами. Рассмотрим первый случай, когда корни действительные. После того, как корни найдены, полином F (p) будет иметь вид ! ! 1 1 F (p) = TэмTя (p − p1 )(p − p2 ) = TэмTя p1 p2 − p + 1 − p + 1 = p1 p2 ! ! ! ! 2 2 Tэм − Tэм + 4TяTэм 1 1 1 1 = − p+1 − p+1 = − p+1 − p+1 . 4TяTэм p1 p2 p1 p2 Обозначим Tд1 = − 1 ; p1 Tд2 = − 1 , p2 тогда F (p) = (Tд1 p + 1)(Tд2 p + 1). Передаточная функция будет иметь вид ω 1 = . Eп k(Tд1 p + 1)(Tд2 p + 1) - - - После разложения на дроби (уточнить термин!) Разложение на дроби произвести самостоятельно. При нулевых начальных условиях и ступенчатом изменении Eп получим следующее выражение для переходной характеристики ! Tд2 Tд1 ω(t) 1 − Tt − Tt д1 д2 = 1+ e − e . ∆Eп k Tд2 − Tд1 Tд2 − Tд1 (16) Оценим начальный участок переходного процесса. Для этого возьмём производную от (16). ! 1 1 1 d ω(t) − Tt − Tt д1 д2 = − e + e . dt ∆Eп k Tд2 − Tд1 Tд2 − Tд1 d ω(t) При t = 0 выражение dt ∆Eп = 0. Это отражает то обстоятельство, что сначала должен вырасти ток якоря, и лишь затем, когда появится динамический момент, начнёт изменяться скорость. Учитывая, что Iя (p) J p/k J ω(p) = · = p , Eп (p) k F (p) k Eп (p) т. е., что Iя (t) J d ω(t) = · . Eп k dt ∆Eп Уточнить, что в передаточной функции Eп — функция, а во временной области просто скачок выражение для тока якоря ! Iя (t) J 1 1 − t − t = 2 − e Tд1 + e Tд2 . ∆Eп Tд2 − Tд1 Tд2 − Tд1 k ? ω 52 Eп3 Eп2 Eп1 ω1 ω2 0 Iяс ω3 Iя Imax Рис. 44. Электромеханические характеристики при регулировании тока и ограничении тока. Из этого равенства очевидно, что по окончании переходного процесса, вызванного изменением Eп , Iя (t)|t→∞ = 0. Это понятно, т. к. установившееся значение тока определяется моментом нагрузки, а изменение момента нагрузки у нас принято равным нулю. Производную тока в начале переходного процесса можно определить по передаточной функции d Iя (t) dt ∆Eп = lim p t=0 p→∞ Iя (p) pTэм p pTэм p = lim · = lim · = Eп (p) p→∞ Rяц F (p) p→∞ Rяц TэмTя p2 + Tэм p + 1 = lim p→∞ p pTэм 1 1 · = = . Rяц TэмTя p2 RяцTя Lяц Т. е. в первый момент времени ток будет изменяться по прямой с наклоном Rяц1Tя . Если бы в якоре двигателя не возникало противоЭДС, то ток изменялся бы по экспоненте с установившимся значением 1/Rяц и с постоянной времени Tя , однако, из-за наличия противоЭДС, кривая будет иметь более сложный вид. Отметим, что чем меньше Tя по сравнению с Tэм , тем ближе бо́льшая из постоянных времени Tд1 и Tд2 к Tэм , а меньшая — к Tя . Рассмотрим второй случай, когда Tэм < 4Tя . Корни при этом комплексно-сопряжённые. Тогда передаточную функцию ω(p) 1 1 . = 2 2 Eп (p) k Tэк p + 2Tэк ξp + 1 Зависимость скорости при ступенчатом изменении ЭДС преобразователя будет иметь вид " !# t ξ ω(t) 1 = 1 − e −ξ Tэк cos ωк t + sin ωк t , ∆Eп k Tэк ωк p 1 − ξ2 — частота затухающих колебаний. Видно, что переходный процесс будет иметь вид где ωк = Tэк затухающих колебаний. (изобразить графики переходных процессов). Далее рассмотрим переходные процессы в ЭП при ограничении тока якоря. Процесс изменения скорости ЭП связан с тем, что при изменении ЭДС преобразователя изменяется ток, а следовательно и момент двигателя. Скорость изменяется из-за того, что момент двигателя и статический момент не уравновешивают друг друга в соответвии с уравнением динамики Mд − Mс = J dω . dt Чем при прочих равных больше изменение ЭДС преоразователя Eп , тем больше броски тока якоря. Между тем, значение динамического тока двигателя не должно превышать некоторого предельно допустимого значения Iя max . Очевидно, что ограничить ток допустимым значением можно, воздействуя на характер изменения ЭДС. На рис. 44 показана электромеханическая характеристика, на которой выделен путь перемещения рабочей точки при ограничении тока. Ограничение тока может осуществляться или переводом преобразователя в режим источника тока, или поддержанием постоянной разности между ЭДС преобразователя и ЭДС якоря двигателя Eп − cE Φω = Iя Rяц . В замкнутых системах регулирования ограничение тока осуществляется с помощью контура тока, на входе которого ставится ограничение на заданное значение тока. Рассмотрим динамику процесса в предположении, что постоянная времени якоря Tя = Lя /Rя много я меньше электромеханической постоянной времени Tэм = JR , где k = cE Φ = cM Φ. В этом случае, постоянной k2 времени якоря можно принебречь. @A B 53 Mс Iз Eз Wрт Wп Eп Iя kя Tя p+1 M kM Eя 1 Jp ω kE Wдт Рис. 45. Структурная схема привода постоянного тока с ограничением тока. Eп3 Iя max kω2 Eп2 Iяс t1 t2 Eп1 kω1 t1 б t а kω3 t2 t3 t Рис. 46. Графики тока а и ЭДС якоря Eя и преобразователя Eп б в функции времени.. Сверху идёт Eп , снизу — Eя = kω; показать Iя max Rяц и Iяс Rяц До начала переходного процесса рабочая точка располагается в точке 0. Ток якоря Iя = Iяс ; ЭДС преобразователя Eп = Eп1 ; скорость Eп1 − Rяц Iяс , ω = ω1 = k где Iяс = Mс /k. В момент времени t1 ЭДС преобразователя скачком увеличивается до значения Eп2 , и рабочая точка скачком перемещается в точку 1. Ток якоря (поскольку мы приняли постоянную времени Tя = 0) скачком изменяется до значения Iя max . Возникает динамический момент Mдин = Mmax − Mс = k · (Iя max − Iяс ). В период времени t1 –t2 на участке 1–2 электромеханической характеристики ток якоря должен оставаться постоянным Iя = Iя max . Процесс разгона определяется уравнением механики k · [Iя max − Iс (t)] = J dω . dt Если момент сопротивления постоянен, а, значит, Iс = const, то двигатель будет увеличивать скорость по линейному закону с постоянным ускорением dω k · (Iя max − Iс ) = . dt J ЭДС двигателя Eя = kω также меняется по линейному закону, а ЭДС преобразователя меняется по закону Eп = Eд + Iя max Rяц . Скорость изменяется от значения ω1 до значения ω2 за время t2 − t1 = J · (ω2 − ω1 ) . k · (Iя max − Iяс ) Теперь рассмотрим период времени t2 –t3 . В момент времени t2 ЭДС преобразователя достигает значения Eп = Eп3 и далее будет оставаться неизменной. Уравнение механики имеет вид dω , kIя − Mс = J dt где Eп − kω Iя = . Rяц 54 После подстановки kEп k2 ω dω . − − Mс = J Rяц Rяц dt Это уравнение первого порядка, описывающее процесс изменения скорости. Перепишем его в виде J dω k2 ω kEп + = − Mс . dt Rяц Rяц или JRяц dω Eп Mс Rяц . +ω= − k k2 dt k2 Правая часть этого уравнения равна скорости ω3 в установившемся режиме работы (в конце переходного процесса) Eп Mс Rяц ω3 = . − k k2 Множетель перед производной по скорости — электромеханическая постоянная времени Tэм = При данных обозначениях уравнение принимает вид Tэм JRяц . k2 dω + ω = ω3 . dt Общее решение этого уравнения имеет вид t ω = Ce− Tэм + ω3 . При t = 0, ω2 = C + ω3 , откуда C = ω2 − ω3 . Общее решение имеет вид t t ω = ω2 e− Tэм + (1 − e − Tэм )ω3 . Система тиристорный преобразователь – двигатель Основной системой регулируемого электропривода с двигателями постоянного тока является система тиристорный преобразователь — двигатель постоянного тока (ТП–Д), наиболее распространенные схемы которой приведены ниже. (Онищенко) Первые две схемы относятся к нереверсивным электроприводам. В этих схемах изменение полярности питающего напряжения и направления тока в якорной цепи невозможно. Последняя — к реверсивным. Основу схем тиристорных преобразователей составляют полууправляемые силовые полупроводниковые приборы — тиристоры. Неполная управляемость тиристоров определяется тем, что при подаче отпирающего импульса на управляющий электрод тиристора он открывается и остается открытым после снятия отпирающего импульса. Закрывается тиристор после изменения полярности напряжения анод–катод и спадания тока до нуля. Запирание тиристоров по цепи управления невозможно. Сказанное выше относится к однооперационным тиристорам. Существуют запираемые тиристоры, которые допускают запирание по цепи управления, однако эти приборы в системах электропривода ТП–Д до настоящего времени широкого применения не нашли. Тиристорный преобразователь в схемах электропривода постоянного тока выполняет две функции: выпрямление переменного напряжения питающей сети и регулирование средней величины выпрямленного напряжения. Принцип регулирования среднего значения выпрямленного напряжения тиристорного преобразователя с импульсно-фазовым управлением рассмотрим на примере однофазной мостовой схемы. Если отпирающие импульсы на тиристоры VS1 и VS4 (и соответственно тиристоры VS2 и VS3 при другой полуволне синусоиды питающего напряжения) подаются в момент естественного открывания, когда напряжение катод–анод становится положительным, то среднее выпрямленное напряжение, определяемое заштрихованной площадью на рис., будет максимальным и равным Ed0 = kсхUл , где Uл — линейное напряжение на стороне переменного тока; kсх — коэффициент схемы выпрямления, который равен для однофазной мостовой схемы 0,9, для трехфазной мостовой схемы — 1,35, и для трехфазной нулевой схемы — 0,675. Если отпирающие импульсы на тиристоры будут подаваться с запаздыванием относительно момента естественного открывания на угол α (угол управления тиристорами), то среднее выпрямленное напряжение преобразователя будет уменьшаться, как это показано на рис. При этом тиристоры VS1 и VS4 будут проводить ток до тех пор, пока не откроются тиристоры VS2 и VS3, т.е. и в то время, когда напряжение CD 55 VS1 VS2 VS3 VS4 Рис. 47. Электрические схемы привода с однофазным а и трёхфазным б нереверсивными выпрямителями. катод–анод будет отрицательным. Это объясняется тем, что в цепи выпрямленного тока имеется достаточно больша́я индуктивность якорной цепи двигателя Lяц , и ток будет протекать под действием ЭДС самоиндукции. Если же в цепи выпрямленного тока не было бы индуктивности (чисто активная нагрузка), то ток прекратился бы при переходе анодного напряжения через нуль; ток в этом случае был бы прерывистым. При достаточно большом значении индуктивности Lяц соотношение между средним выпрямленным напряжением преобразователя и углом α будет Ed = Ed0 cos α. (17) Среднее выпрямленное напряжение определяется разностью заштрихованных площадей. При значении угла регулирования α = π/2 среднее выпрямленное напряжение будет равно нулю. Тиристорный преобразователь может работать в выпрямительном и в инверторном режимах. Выпрямительный режим имеет место при углах регулирования 0 6 α < π/2. При этом среднее выпрямленное напряжение должно быть больше ЭДС в цепи выпрямленного тока (противоЭДС якоря двигателя) Ed > Eя . Направление выпрямленного тока совпадает со знаком выпрямленного напряжения преобразователя. Если угол α будет больше π/2 (π/2 < α < π), то площадь отрицательной полуволны, при которой открыты тиристоры, будет больше площади положительной полуволны (см.рис. г) и, следовательно, среднее выпрямленное напряжение преобразователя будет отрицательным, что следует также из формулы (17). Возникает инверторный режим работы преобразователя, который может быть использован для обеспечения рекуперативного торможения привода. Под действием отрицательного напряжения преобразователя ток пойти не может из-за односторонней проводимости тиристоров. Поэтому инверторный режим преобразователя возможен при соблюдении трех условий: 1. В цепи выпрямленного тока ЭДС якоря двигателя должна быть больше Ed инвертора Ed > |Eя |. 2. Источник ЭДС (якорь двигателя) должен быть так подключен к преобразователю, чтобы было возможно протекание тока под действием ЭДС якоря. 3. Угол управления тиристорами должен быть α > π/2. При соблюдении этих условий двигатель постоянного тока будет работать в генераторном режиме, вырабатывая энергию постоянного тока, которая преобразуется тиристорным преобразователем в энергию 56 E Рис. 48. Электрическая схема привода с трёхфазным реверсивным выпрямителем. переменного тока и отдаётся в питающую сеть. Электропривод ТП–Д, в котором двигатель питается от двух встречно-включенных преобразователей, называется реверсивным (см. рис.). Для обеспечения второго условия при переходе из двигательного режима в генераторный необходимо или изменить полярность на якоре двигателя, что осуществляется с помощью специального автоматически переключаемого устройства — реверсора, или изменить направление ЭДС двигателя, что осуществляется изменением направления потока возбуждения, т. е. изменением полярности питающего напряжения обмотки возбуждения. Недостаток последнего способа является больша́я длительность, обусловленая большой электромагнитной постоянной времени обмотки возбуждения (до 1,5 с). Отметим, что выпрямленный ток имеет непрерывный характер, если индуктивность в цепи выпрямленного тока достаточно велика (Lяц → ∞). Если ток якоря принимает прерывистый характер, тогда механические характеристики привода становятся нелинейными (см. рис.). При конечных значениях индуктивности в цепи выпрямленного тока на условие непрерывности тока оказывают также влияние величина тока и угол регулирования. Граничное (минимальное) значение тока, при котором ток еще остается непрерывным определяется соотношением Iгр = π π Ed0 sin α 1 − ctg . ωс Lяц m m (18) где ωс — частота переменного тока, рад/с; m — число коммутаций за период (пульсность схемы). Для однофазной мостовой схемы m = 2, для схемы Ларионова трёхфазной мостовой m = 6. Влияние режима прерывистого тока проявляется в увеличении среднего значения выпрямленного напряжения в зоне прерывистого тока. Если полагать, что привод работает в режиме непрерывного тока (при Lяц → ∞), то механические характеристики будут иметь вид наклонных прямых параллельных друг другу, причем ω0 уменьшается по мере уменьшения выпрямленного напряжения (увеличения угла α). 57 Рис. 49. Эпюры напряжений однофазного мостового тиристорного преобразователя при различных углах управления α. Рис. 51. Электромеханические характеристики привода ТП–Д при раздельном управлении комплектами преобразователей. Рис. 50. Электромеханические характеристики системы ТП–Д в режимах непрерывного и прерывистого токов. Механические характеристики описываются в этом случае следующей формулой ω= Rяц Ed0 cos α − · M. cE Φ cE cM Φ2 При конечных значениях индуктивности якорной цепи Lяц в области малых значений момента (тока якоря) — левее граничной линии механические характеристики теряют линейность и загибаются вверх. Это является следствием перехода в зону прерывистых токов. Линия, определяющая границу непрерывного тока, определяется уравнением (18). При желании уменьшить зону прерывистых токов последовательно с якорем двигателя включают сглаживающий дроссель, величина индуктивности которого может быть определена по формуле Lдр > π π Ed0 1 − ctg − Lя , 2πfс Iгр тр m m где fс — частота переменного тока, Гц; Iгр тр — требуемое значение граничного тока; Lя — индуктивность якоря двигателя с учётом дополнительных полюсов и компенсационных обмоток. В том случае, когда угол управления тиристорами α < π/m, где m — пульсность схемы, скорость идеального холостого хода не зависит от α, т. к. в таком режиме ЭДС двигателя будет соответствовать 58 максимальной ЭДС преобразователя, которая будет соответствовать макимальному напряжению сети за вычитом падения напряжения на вентилях преобразователя. Это объясняется тем, что даже при наличии отпирающих импульсов пока мгновенное значение ЭДС преобразователя eп (t) не превысит мгновенное значение ЭДС двигателя eя (t), тиристоры не открываются, и энергия из сети в двигатель не поступает. Когда ЭДС преобразователя станет превышать ЭДС двигателя, и если в это время будет подан отпирающий импульс, через якорь начнёт протекать ток. Когда ЭДС преобразователя станет меньше ЭДС двигателя, ток ещё будет протекать под действием ЭДС самоиндукции якорной цепи, но когда он снизится до нуля, тиристоры закроются. На холостом ходу противоЭДС двигателя практически равна макимальной ЭДС преобразователя. ВСТАВИТЬ РИСУНОК ACAD21! Рис. 52. Диаграмма работы однофазного выпрямителя в режиме прерывистых токов при угле управления α 6 π2 .. Вопрос — где должен приходиться максимум тока? Если бы не падение напряжения на Rяц , то в той точке, где eп = eя . Если бы нагрузка была чисто активной... Следует отметить, что изображённое на рисунке небольшое снижени ЭДС двигателя объясняется механическими потерями холостого хода. В случае идеального холостого хода ЭДС двигателя снижаться не будет. Когда угол управления тиристорами α > π/m скорость холостого хода будет уже определяться не максимальным линейным напряжением сети, а мгновенным значением линейного напряжения сети в момент открывания ключей. При этом скорость холостого хода будет зависеть от угла управления тиристоров α. В общем виде формула для расчёта скорости идеального холостого хода будет иметь вид Eс max − ∆Uв , при 0 6 α < mπ ; cE Φ ω0 = Eс max cos α − mπ − ∆Uв , при α > mπ , cE Φ где Eс max — максимальное линейное напряжение сети; ∆Uв — падение напряжения на вентилях. Механические характеристики системы ТП–Д, работающей в режиме прерывистых токов, не могут быть выражены аналитически, поскольку их координаты зависят от угла проводимости тока λ, и строятся численно. Заметим, что механические характеристики нереверсивного привода ТП–Д не переходят ось ординат, т. к. изменение направления тока в нереверсивных схемах невозможно. Следовательно, отсутствует режим рекуперативного торможения. В случае необходимости изменения направления вращения приводного двигателя в нереверсивных приводах по системе ТП–Д изменяют направление тока в обмотке возбуждения двигателя. 59 ВСТАВИТЬ РИСУНОК ACAD22! Рис. 53. Диаграмма работы однофазного выпрямителя в режиме прерывистых токов при угле управления α > π2 .. Для того, чтобы получить электропривод, работающий во всех четырех квадрантах, необходимо использование реверсивного тиристорного преобразователя, обеспечивающего протекание тока якоря в обоих направлениях. Реверсивные тиристорные преобразователи содержат две группы тиристоров, включенные встречно-параллельно друг другу. Наиболее распространенная схема — два тиристорных преобразователя UZ(B) и UZ(H), собранные каждый по трехфазной мостовой схеме, включены параллельно друг другу с противоположной полярностью на стороне выпрямленного тока. Подавать отпирающие импульсы одновременно на обе группы тиристоров нельзя, т.к. произойдет короткое замыкание. Поэтому в данной схеме может работать только одна группа тиристоров UZ(B) или UZ(H); другая группа должна быть закрыта (отпирающие импульсы сняты). Такая реверсивная схема называется схемой с раздельным управлением группами тиристоров. При раздельном управлении включается только та группа тиристоров, которая в данный момент должна проводить ток. Выбор этой группы зависит от направления движения привода («вперед» или «назад») и от режима работы: двигательный режим или рекуперативное торможение. Раздельное управление имеет следующие недостатки. Перевод привода из двигательного режима в тормозной сопровождается паузой, что увеличивает его инерционность. Раздельное управление не применимо в приводах, требующих плавного перехода из двигательного в тормозной режим. Например, в лифтах и грузоподъемных устройствах вблизи точки идеального холостого хода будут возникать области неуправляемости привода, сопровождаемые рывками усилий и провалами скорости. Для устранения этих недостатков применяют преобразователи с совместным управлением. При совместном управлении управляющие сигналы подаются на оба комплекта преобразователей. Один из преобразователей работает в режиме выпрямителя, а другой — инвертора. Но при этом между ними в силовой цепи привода возникают уравнительные токи ввиду разности ЭДС преобразователей. Для их ограничения используют четыре уравнительных реактора 1Р–4Р. Кроме того, для сглаживания пульсаций тока в якоре двигателя имеется реактор Р. В этом случае при использовании линейного согласования удаётся получить линейные механические характеристики. По сравнению с совместным раздельное управление имеет следующие преимущества: возможность полного использования трансформатора в том случае, если преобразователь питается от трансформатора; полное исключение уравнительных реакторов; снижение вероятности опрокидывания инвертора; уменьшение потерь и увеличение КПД привода. 60 F Рис. 54. Привод с трёхфазным реверсивным выпрямителем с согласованным управлением. Лекция №9 Механические и электромеханические характеристики ЭП с ДПТ последовательного возбуждения. Способы регулирования скорости. Механические характеристики привода при шунтировании якоря. Механические и электромеханические характеристики ЭП с ДПТ последовательного возбуждения. Двигатели последовательного возбуждения (ДПТ ПВ) ещё в 70-е годы широко применялись в металлургическом производстве, подъемно-транспортном оборудовании, таких приводах, как рольганги, сбрасыватели, подъемные краны, лифты, нажимные механизмы, рабочие рольганги, манипуляторы, ножницы. В настоящее время они существенно меньше применяются, уступая место АД с короткозамкнутыми роторами и частотными преобразователями. Для приводов, требующих постоянной скорости при меняющейся нагрузке, из-за мягкости характеристик ДПТ ПВ непригодны. Тем не менее, эти двигатели продолжают широко применяться в электротяге: в трамваях, средствах внутризаводского транспорта, где постоянный ток выгоден тем, что достаточно использовать один троллей. При питании асинхронного двигателя от преобразователя частоты разрывы связи между преобразователем частоты и двигателем недопустимы, т. к. могут привести к выходу силовых транзисторов преобразователя из строя. При троллейной подаче питания из-за вибраций происходят частые прерывания контактов, из-за которых использование систем ПЧ–АД весьма затруднено. Установка ПЧ непосредственно на тележках внутрицехового транспорта также оказывается не всегда возможной, из-за высокого уровня вибрации, или по иным технологическим причинам. В таких случаях приводы с ДПТ оказываются наиболее разумным решением, поскольку в достаточной степени нечувствительны к разрывам питающей сети. К достоинствам ДПТ ПВ по сравнению с ДПТ НВ относится то, что они удовлетворительно работают и при больши́х снижениях напряжения, что характерно при больших протяженностях троллейного питания. Кроме того, ДПТ ПВ при перегрузках механизмов развивают бо́льшие моменты по сравнению с ДПТ НВ G H 61 при одинаковых перегрузках по току. А также они более надежны, благодаря повышенному сечению обмотки возбуждения, малым напряжениям между её витками и отсутствию систем гашения поля для обмоток возбуждения. В двигателе последовательного возбуждения обмотка возбуждения включена последовательно в цепь якоря. Для изменения направления вращения двигателя последовательного возбуждения недостаточно изменить полярность напряжения, подводимого к двигателю, т.к. при этом изменится одновременно и направление тока в обмотке якоря, и полярность потока возбуждения. Поэтому для реверсирования двигателя нужно изменить направление тока в одной из частей машины, например в обмотке якоря, оставив направление тока в обмотке возбуждения неизменным. В Н Н Rдоб В Рис. 55. Электрическая схема включения привода постоянного тока последовательного возбуждения в двигательном режиме. KB KM RB KM KB Рис. 56. Электрическая схема включения привода постоянного тока последовательного возбуждения в тормозном режиме. Магнитный поток ДПТ ПВ является функцией тока якоря. Поэтому при увеличении нагрузки на валу двигателя скорость вращения последнего изменяется как за счёт падения напряжения в цепи якоря, так и за счёт увеличения потока. Это и обуславливает значительную крутизну его механических характеристик. Уравнение механической характеристики двигателя последовательного возбуждения даже в случае ненасыщенной магнитной цепи имеет весьма сложный вид. Если магнитный поток линейно зависит от тока возбуждения (Φ = αIя , где α — коэффициент пропорциональности), то момент двигателя пропорционален квадрату магнитного потока M = cM ΦIя = cM αIя2 = cM Φ2 /α, откуда s Φ= αM . cM Следует отметить, что в действительности коэффициент α зависит от величины тока двигателя, эта зависимость связана с формой кривой намагничивания и размагничивающим действием реакции якоря; оба этих фактора проявляются при больших токах Iя > (0,7 . . . 0,8)Iян ; при малых токах якоря коэффициент α можно считать величиной постоянной. При токах якоря Iя > 2Iян машина насыщается, и величина потока мало зависит от тока якоря. Подставляя выражения для тока и потока в уравнение механической характеристики, получим ω= ω= cE MRяц Eп − ; cE Φ cE cM Φ2 Eп q αM cM − cM αIя2 Rяц ; cE cM α2 Iя2 62 √ Eп cM Rяц . − √ cE αM cE α Учитывая, что при использовании основных единиц СИ cM = cE , ω= ω= √ Eп cE αM − Rяц . cE α или Rяц Eп a . где a = √ иb= ω = √ − b, c c α Eα E M Аналогично для электромеханической характеристики получим выражение ω= (19) Iя Rяц Eп − ; cE Φ cE Φ Iя Rяц Eп − ; cE αIя cE αIя Rяц Eп ω= − ; cE αIя cE α ω= ω= a0 − b, Iя где a0 = Eп . cE α (20) Из выражений (19) и (20) видно, что момент двигателя пропорционален квадрату тока M ∼ Iя2 . Это объясняется тем, что при увеличении тока якоря пропорционально увеличивается и поток возбуждения. В первом приближении механическую характеристику двигателя постоянного тока последовательного возбуждения, если не учитывать насыщение магнитной цепи, можно представить в виде гиперболы, не пересекающей ось ординат, а асимптотически приближающуюся к ней. Если положить Rяц = 0, то характеристика (если не учитывать насыщения) не будет пересекать и ось абсцисс. Такая характеристика называется «идеальной»; выше нее характеристики быть не могут. I Современные двигатели, как правило, уже в номинальном режиме имеют значительное насыщение магнитной системы. Поэтому гиперболическая зависимость может существовать лишь при малых значениях моментов. При больших моментах, превышающих номинальный, магнитный поток становится практически постоянным. Реальная естественная характеристика пересекает ось абсцисс в точке, соответствующей току короткого замыкания (момент Mк ). Если учитывать насыщение двигателя, то при моментах меньших 0,8Mк механическая характеристика криволинейна и носит гиперболический характер; при больших значениях тока и Φ Iв 63 момента поток вследствие насыщения становится постоянным, и механическая характеристика приобретает линейный характер, близкий к характеристике ДПТ НВ с потоком возбуждения равным потоку насыщения Φ = Φнас. MRяц Eп ω= − . cE Φнас. cE cM Φ2нас. Характерной особенностью характеристик двигателя последовательного возбуждения является отсутствие точки идеального холостого хода. При уменьшении нагрузки скорость двигателя существенно возрастает, вследствие чего оставлять двигатель без нагрузки недопустимо. Нагрузка привода должна составлять не менее 15 . . . 20 % от номинальной [Сандлер стр. 69]. При уменьшении нагрузки машины, работающей в двигательном режиме, происходит снижение магнитного потока и повышение скорости вращения до 5–6-кратного номинального значения. Может быть превзойден предел механической прочности бандажей, крепящих обмотку якоря, и «разнос» двигателя. Поэтому режим холостого хода недопустим. Важным достоинством двигателей последовательного возбуждения является большая перегрузочная способность на низких скоростях. При перегрузке по току в 2,25 . . . 2,50 раза двигатель развивает момент 3,0 . . . 3,5 номинального. Это обстоятельство определило широкое использование двигателей последовательного возбуждения для электрических транспортных средств, где наибольшие моменты необходимы при трогании с места, и отсутствуют режимы работы на холостом ходу. Вторым важным достоинством двигателей последовательного возбуждения является отсутствие источника питания для цепи возбуждения двигателя. Попытки найти приближенное математическое выражение механической характеристики двигателя последовательного возбуждения с учетом насыщения не увенчались успехом из-за возникающих затруднений с нахождением коэффициентов уравнений, аппроксимирующих кривую намагничивания, сложности получающихся приближенных выражений и невозможности их использования в практических расчётах. Поэтому при всякого рода расчетах приводов с двигателем последовательного возбуждения прибегают к графическим и графоаналитическим методам, используя экспериментально полученные зависимости его скорости вращения, момента и КПД в функции тока якоря, учитывающие как насыщение, так и влияние реакции якоря. Способы регулирования скорости Искусственные механические характеристики могут быть получены различными способами: включением добавочного сопротивления в цепь якоря, изменением величины питающего напряжения и шунтированием обмотки якоря или обмотки возбуждения добавочным сопротивлением. При введении добавочного сопротивления в цепь якоря жесткость механических характеристик уменьшается и уменьшается значение Mк . Уменьшение Mк объясняется тем, что при заторможенном роторе через якорь двигателя будет протекать меньший ток. (Ток будет ограничиваться добавочным сопротивлением.) Этот способ регулирования используется при пуске двигателя, когда ступени сопротивления перемыкаются пусковыми контакторами. Длительная работа на реостатных характеристиках сопряжена со значительными потерями энергии в сопротивлениях. Из полученных нами выражений видно, что при увеличении сопротивления та часть характеристики, которая соответствует ненасыщенной машине, опускается вниз параллельно себе самой, и, следовательно, жёсткость её не меняется. Та часть характеристики, которая соответствует насыщенной машине, описывается тем же уравнением, что характеристика ДПТ НВ, и при увеличении сопротивления её жёсткость уменьшается. Наиболее экономичным способом регулирования скорости двигателя последовательного возбуждения является изменение величиины подводимого к двигателю напряжения. По мере уменьшения напряжения механичесекие характеристики смещаются вниз. Причём, та часть характеристики, которая соответствует JK 64 насыщенной машине, смещается параллельно естественной характеристике, а та часть, которая соответствует ненасщенной машине, становится более жёсткой, в чём можно убедиться, взяв производную от выражения (19). В том случае, когда требуется получить скорость вращения, превышающую номинальную, осуществляют ослабление магнитного потока посредством шунтирования обмотки возбуждения сопротивлением. Rш Rш Rп Rп В случае Rш → ∞ будем иметь нормальную схему включения двигателя, так как при этом Iя = Iв . При ш Rш < ∞ ток в обмотке возбуждения равен Iв = Iя · RшR+R . Поэтому при шунтировании обмотки возбуждения в магнитный поток будет меньше, чем при работе по нормальной схеме включения двигателя. Следовательно, скорость будет выше. Общий вид механической характеристики сохранится, но вся она сместится в сторону бо́льших скоростей. Механические характеристики привода при шунтировании якоря Включая сопротивление, шунтирующее только обмотку якоря, можно регулировать поток взбуждения. В этом случае ток возбуждения будет равен Iв = Iя + Uя . Rш При этом возникает возможность протекания тока по обмотке возбуждения при отсутствии тока в цепи якоря. Это обстоятельство не только обеспечивает возможность работы при холостом ходе, но в некоторых пределах даже позволяет иметь режим генераторного торможения. Увеличение магнитного потока за счет влияния тока шунтирующего контура, а также дополнительное падение напряжения от этого тока в последовательном сопротивлении приводят к значительному снижению скорости. Уменьшение величины шунтирующего сопротивления сдвигает характеристику вниз и влево во второй квадрант. «Скорость идеального холостого хода» будет иметь место, когда ЭДС якоря станет равной падению напряжения в шунтирующем сопротивлении, создаваемому током, протекающим по этому сопротивлению, обмотке возбуждения и последовательному сопротивлению. При дальнейшем повышении скорости якорь совместно с сетью начинает питать шунтирующий контур, отчего ток в нем увеличивается. Результатом этого является увеличение падения напряжения на зажимах шунтирующего сопротивления и, как следствие, ослабление магнитного потока. Поэтому при некоторой скорости тормозной момент достигает максимума, а затем с увеличением скорости начинает уменьшаться. Уменьшение шунтирующего сопротивления снижает пусковой момент и повышает жёсткость характеристики в двигательном режиме. В этом случае торможение противовключением не применимо, так как оно дает чрезмерно большие значения тормозного момента. В зоне динамического торможения характеристики имеют значительную крутизну. Существенным недостатком рассматриваемого способа регулирования является его неэкономичность, обусловленная большими потерями энергии в шунтирующем сопротивлении. Тормозные режимы двигателя последовательного возбуждения Возможности ДПТ ПВ в тормозных режимах более ограничены, чем машин независимого возбуждения. Так, невозможно осуществить генераторное торможение с отдачей энергии в сеть. Режим динамического торможения можно осуществить при самовозбуждении машины. изобразить схему. Его сущность состоит в том, что двигатель, отключённый от сети, замыкается на тормозное сопротивление и работает в качестве генератора с самовозбуждением. При вращении за счет кинетической энергии 65 механизма или под действием активного момента в якоре от остаточного намагничивания будет индуктироваться ЭДС. Следует иметь в виду, что при переходе из двигательного режима в режим динамического торможения необходимо сохранить направление тока в обмотке возбуждения во избежание размагничивания машины. При размыкании контактора KM ток в обмотке возбуждения становится равным нулю, но, так как магнитопровод машины был намагничен, то сохраняется остаточный поток возбуждения, благодаря которому в обмотке якоря вращающегося двигателя наводится ЭДС, под действием которой при замыкании контактов KB в цепи обмотка якоря — обмотка возбуждения — сопротивление R протекает ток, и машина самовозбуждается. Однако процесс самовозбуждения будет происходить, если скорость двигателя будет больше граничной скорости. Более строго, самовозбуждение имеет место только в том случае, если ЭДС машины, определяемая величиной магнитного потока и скоростью вращения, больше падения напряжения в сопротивлении тормозного контура, т. е. Eя > Iя · (Rя + Rв + Rт ), где Rв — сопротивление обмотки возбуждения; Rт — тормозное сопротивление, на которое замкнута цепь якоря. При некоторой скорости будет достигнуто равновесие, т. е. когда ЭДС якоря и падение напряжения на сопротивлении якорной цепи будут равны. При этом режим работы двигателя определится точкой пересечения кривой намагничивания1 Eя = f (Iя ) при достигнутой скорости вращения с линией, характеризующей падение напряжения в цепи якоря f (Iя ) = Iя · (Rя + Rв + Rт ). Механическая характеристика будет иметь следующий вид... Недостатком этого метода является низкая плавность торможения. В том случае, когда привод начинает раскручиваться под действием активного момента, вначале тормозной момент мал. При увеличении скорости происходит самовозбуждение машины, и тормозной момент резко возрастает, что приводит к рывкам и большим динамическим нагрузкам на приводной механизм. Что может быть недопустимо. Поэтому, этот режим находит очень ограниченное применение. Для получения большей плавности торможения прибегают к динамическому торможению с независимым возбуждением. Оно более эффективно при малых скоростях. Однако при этом затрачивается на создание номинального магнитного потока почти номинальная мощность, ввиду наличия большого добавочного сопротивления. Это экономически не выгодно. Изобразить схему. Основным тормозным режимом для этих машин является противовключение. Оно осуществляется (при реактивном статическом моменте) изменением полярности напряжения на якоре и введением добавочного сопротивления Rп . Тогда двигатель переходит из точки A, характеризующей его установившийся режим до начала торможения, в точку B, приобретая тормозной момент. Участок характеристики BC соответствует режиму противовключения, а участок CD — режиму реверса. Возможно отключение добавочного сопротивления Rп и вывод двигателя на естественную характеристику с параметрами установившегося режима, соответствующего точке A0 . При активном статическом моменте режим противовключения получают только введением в цепь якоря добавочного сопротивления Rп . Тогда двигатель переключается из начальной точки работы A в точку B новой характеристики. На участке BC он работает в двигательном режиме, а на участке CD этой же характеристики — в режиме противовключения. В точке установившегося движения D двигатель развивает тормозной момент, уравновешивающий движущий момент механизма Mс . 1 Проверить термин. Так у Андреева и Ковчина написано. LM ВТОРОЙ ТЕКУЩИЙ КОНТРОЛЬ 66 67 Тема №5 Электропривод переменного тока с разомкнутой системой регулирования (22 часа) Физические процессы в электроприводе переменного тока с разомкнутой системой управления. Математическое описание электропривода с АД в виде схемы замещения. Механические характеристики и способы регулирования скоростей воздействием на цепи статора и ротора. Понятие о векторном описании ЭП с АД и разомкнутой системой управления. Статические характеристики ЭП с синхронным двигателем. Понятие о двигателе с вентильно-индукторным двигателем.