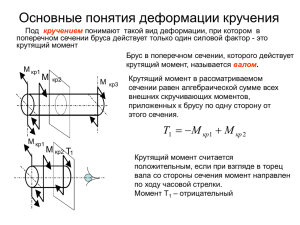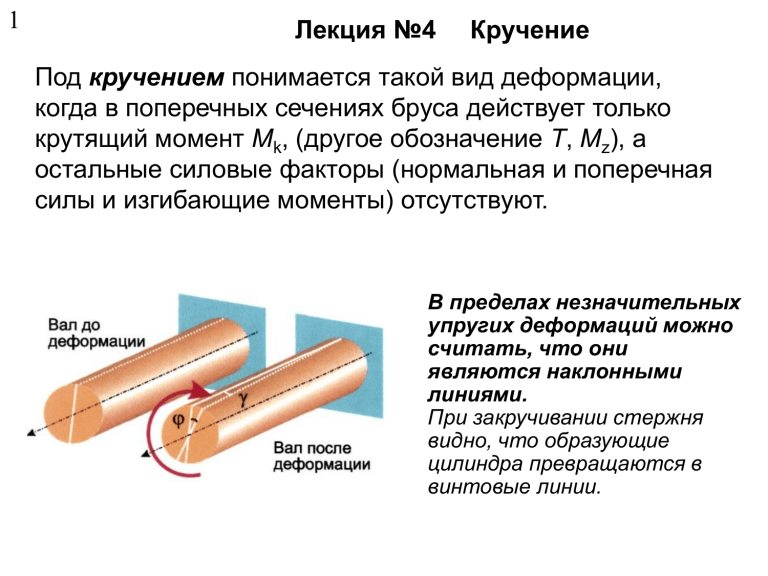
1 Лекция №4 Кручение Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент Mk, (другое обозначение T, Mz), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют. В пределах незначительных упругих деформаций можно считать, что они являются наклонными линиями. При закручивании стержня видно, что образующие цилиндра превращаются в винтовые линии. Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п. Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы). Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала. •На основании метода сечений крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к валу по одну сторону от рассматриваемого сечения. TK Ti В простейшем случае крутящий момент Mz в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M1|=|M2|. Построение эпюр крутящих моментов При расчетах на прочность и жесткость знак крутящего момента не имеет значения, но для удобства построения эп. Mk примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части вала действующий на него момент представляется направленным по ходу часовой стрелки Изобразим стержень, жестко защемленный в правом концевом сечении, к которому приложены три внешних скручивающих момента. M1=200 Нм M2 =200-300=-100 Нм M3 =200-300+500= =400 Нм Принятые предпосылки 1. Поперечные сечения плоские до деформации остаются плоскими и после деформации (гипотеза плоских сечений – гипотеза Бернули). 2. Расстояния между поперечными сечениями остаются неизменными после деформации. 3.Радиусы в поперечных сечениях остаются прямыми и лежат в тех же плоскостях, но при этом поворачиваются на некоторый угол. Геометрическая сторона задачи При кручении происходит поворот сечений друг относительно друга, т. е. они как бы сдвигаются друг относительно друга, поэтому при таком нагружении, будет присутствовать деформация сдвига. δ τ τ а γ τ =G - Закон Гука при сдвиге E G 2 1 - модуль сдвига τ Для стали G = 8*1010 Па При закручивании стержня видно, что образующие цилиндра превращаются в винтовые линии. В пределах незначительных упругих деформаций можно считать, что они являются наклонными линиями. Закон распределения касательных напряжений по сечению круглого сечения d G dz TK I Определение перемещений при кручении Для постоянного сечения с постоянным моментом Расчеты на прочность и жесткость при кручении. Условие прочности при кручении имеет вид: max TK W По условию прочности при кручении выполняют три вида расчетов. 1. Проектировочный расчет. Определив крутящий момент в сечении бруса и приняв , находим требуемое значение полярного момента сопротивления: Затем, исходя из формулы поперечного сечения (круг или кольцо), находим диаметр бруса. Полученное значение диаметра в миллиметрах следует округлить до ближайшего большего четного числа или числа, оканчивающегося на 5. 2. Проверочный расчет. Определив максимальный крутящий момент в поперечном сечении бруса и полярный момент сопротивления, находим max TK W 3. Расчет допускаемой нагрузки. Определив полярный момент сопротивления сечения бруса, и приняв , находим допускаемое значение крутящего момента: TK W Затем, исходя из схемы нагружения, находим допускаемую нагрузку. : Условие жесткости при кручении состоит в том, чтобы угол закручивания не превосходил некоторого заданного допускаемого значения TK l G I В Международной системе единиц (СИ) допускаемый угол закручивания выражается в рад м в практике часто допускаемый угол закручивания задается в град м умножив на отношение 180 TK l 180 G I Кручение стержней некруглого поперечного сечения Решение задач на кручение стержней некруглого сечения требует более сложного математического анализа и может выполнена лишь методами теории упругости. На практике используют расчетные формулы, полученные эмпирическим путем. Например, для прямоугольного сечения максимальные касательные напряжения будут по середине длинной стороны прямоугольника. A max TK WK Расчет цилиндрический винтовых пружин с малым шагом витка Цилиндрические винтовые пружины относятся к упругим элементам, широко применяемым в машиностроении и приборостроении. Их используют в качестве амортизаторов или аккумуляторов механической энергии, в установках передачи сил давления и в механизмах возврата детали в исходное положение. Винтовая пружина при расчетах рассматривается как пространственный изогнутый брус, осевая линия которого представляет собой винтовую линию. Условие прочности max k 8 F c 2 d где допускаемое напряжение 400...1000 Н мм 2 Под действием нагрузки F пружина растяжения удлиняется, а пружина сжатия укорачивается. Удлинение или укорочение (осадка) пружины определяется по формуле: 8 F D n , 4 Gd 3 где n – число рабочих витков пружины