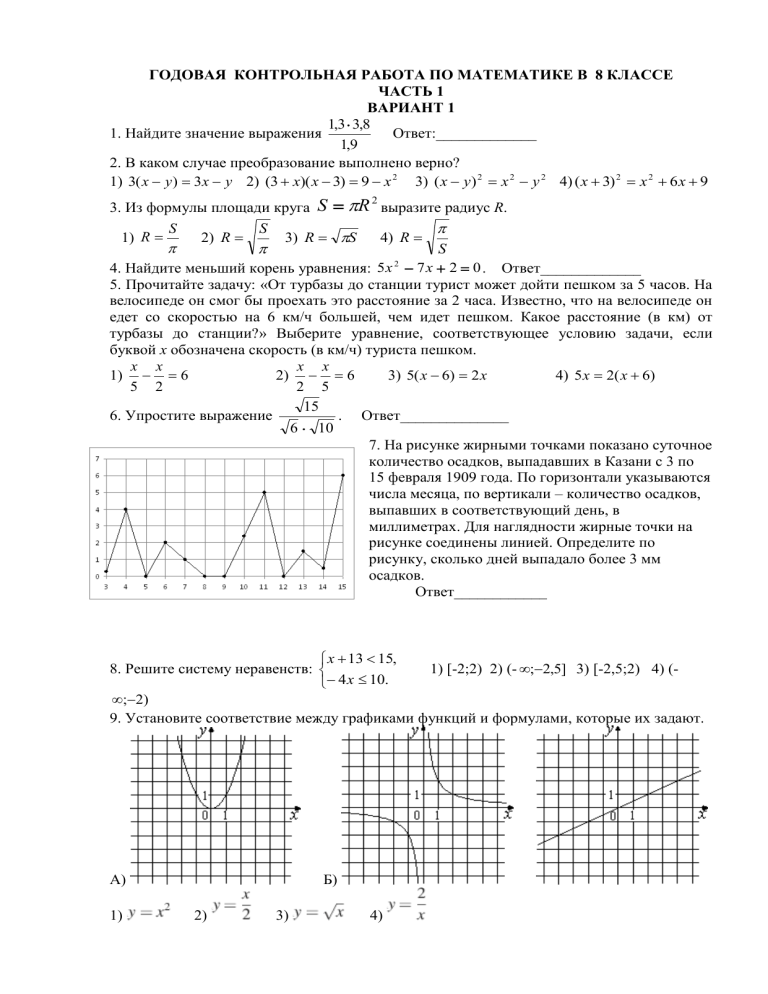
ГОДОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ В 8 КЛАССЕ ЧАСТЬ 1 ВАРИАНТ 1 1,3 3,8 1. Найдите значение выражения Ответ:_____________ 1,9 2. В каком случае преобразование выполнено верно? 1) 3( x y ) 3x y 2) (3 x)( x 3) 9 x 2 3) ( x y) 2 x 2 y 2 4) ( x 3) 2 x 2 6 x 9 3. Из формулы площади круга S R выразите радиус R. S S 1) R 2) R 3) R S 4) R S 2 4. Найдите меньший корень уравнения: 5 х 7 х 2 0 . Ответ_____________ 5. Прочитайте задачу: «От турбазы до станции турист может дойти пешком за 5 часов. На велосипеде он смог бы проехать это расстояние за 2 часа. Известно, что на велосипеде он едет со скоростью на 6 км/ч большей, чем идет пешком. Какое расстояние (в км) от турбазы до станции?» Выберите уравнение, соответствующее условию задачи, если буквой х обозначена скорость (в км/ч) туриста пешком. x x x x 1) 6 2) 6 3) 5( x 6) 2 x 4) 5 x 2( x 6) 5 2 2 5 15 6. Упростите выражение . Ответ______________ 6 10 7. На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 3 мм осадков. Ответ____________ 2 х 13 15, 8. Решите систему неравенств: 1) [-2;2) 2) (- ;2,5] 3) [-2,5;2) 4) ( 4 x 10. ;2) 9. Установите соответствие между графиками функций и формулами, которые их задают. А) 1) Б) 2) 3) 4) А Б В 10. При проектировании торгового центра запланирована постройка эскалатора для подъёма на высоту 4,5 м под углом к горизонту 30 о Найдите длину эскалатора (в метрах). 11. Выберите верные утверждения: 1) Если две окружности касаются, то расстояние между их центрами равно сумме радиусов. 2)Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны. 3) Если в четырехугольнике две стороны параллельны, то этот четырехугольник — параллелограмм. 4) Если один из углов параллелограмма равен , то противоположный ему угол равен . ЧАСТЬ 2 12. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции. 1 a2 13. Упростите выражение a 1 . : a 1 1 2a a 2 14. При каких значениях параметра m уравнение 4 x 2 mx m 3 0 имеет один корень? 15.Расстояние между двумя станциями 420 км. Два поезда вышли из них одновременно и встретились через 3ч. Найдите скорость каждого, если у одного на 20 км/ч больше чем другого. ГОДОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ В 8 КЛАССЕ ЧАСТЬ 1 ВАРИАНТ 2 0,3 1. Найдите значение выражения Ответ_______ 3 1 4 2 2. Упростите выражение 6 х х 3 . 1) х 2 12 х 9 2) х 2 6 х 9 3) х 2 9 4) x 2 9 3. Из формулы F k 1) q 2 F r2 k q1 q1 q2 выразите q 2 . r2 2) q 2 k F r 2 q1 F r2 3) q 2 k q1 4) q 2 F r2 k q1 4. Найдите больший корень уравнения: 4 х 2 3х 1 0 . Ответ_____________ 5. Прочитайте задачу: «Саша прочитал книгу за 5 дней, а Илья эту же книгу прочитал за 7 дней. Сколько станиц в день читал Илья, если Саша читал в один день на 12 страниц больше, чем Илья?» Выберите уравнение, соответствующее условию задачи, если буквой х обозначено число станиц, которые в один день читал Илья. 1) 7х 12 5х 2) 7 х 5х 12 3) 5х 7 х 12 4) 7 х 5х 12 6. Упростите выражение 5 27 . Ответ______________ 12 7. При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси – напряжение в вольтах. Определите по рисунку, какое напряжение будет в цепи через 5 часов работы фонарика. Ответ дайте в вольтах. Ответ____________ х 7 11, 7 7 7 8. Решите систему неравенств: 1) (- ; ] 2) [ ;4) 3) [- ;4) 4) (4; 3 3 3 3 x 7. + ) 9. Установите соответствие между графиками функций и формулами, которые их задают 1)у=3х 2) у=х 2 +3х 3) у=3 х 4) у= - 3 х А Б В 10. На рисунке изображен параллелограмм ABCD, внешний угол при вершине А равен 112 о . Найдите CDH, если DH – высота. 11. Выберите верные утверждения: 1) Если радиус окружности и расстояние от центра окружности до прямой равны 2, то эти прямая и окружность касаются. 2) Вписанные углы окружности равны 3) Если дуга окружности составляет , то центральный угол, опирающийся на эту дугу, равен . 4) Диагонали параллелограмма равны. ЧАСТЬ 2 12. В прямоугольном треугольнике с прямым углом , . Найдите медиану этого треугольника. известны катеты: а2 a2 1 13. Упростите выражение a . a 1 a 2 2а 14. При каких значениях параметра а уравнение аx 2 5 x 15 0 не имеет корней? 15. Катер прошёл по течению реки 8км, и вернулся обратно, потратив на весь путь 5ч. Скорость течения реки 3 км/ч. Какова собственная скорость катера?