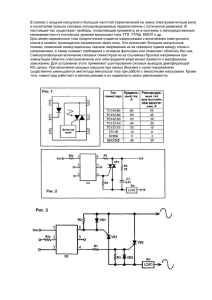
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА Задача №6.1 Электрическая цепь имеет в своем составе идеальный источник ЭДС, катушку индуктивности и четыре резистора. В момент времени t=0 в цепи происходит коммутация. Определить токи ветвей цепи и напряжений на реактивном элементе во время переходного процесса. Построить графики изменения тока и напряжения на реактивном элементе. Исходные данные приведены в таблице. Таблица 1 Шифр 421 E, В 95 r1, Ом 16 r2, Ом 18 r3, Ом 14 r4, Ом 12 r2 r1 r3 r4 E C Рисунок 1 – Схема электрической цепи С, мкФ 45 Решение 1. На схеме после коммутации укажем направления тока в схеме. r2 iC (t ) r3 r1 E C Рисунок 2 – Схема цепи в момент коммутации 2. Находим по закону Ома независимые начальные условия для схемы до коммутации ключа. r2 i2 (0) r3 r1 r4 E uС (0 ) Рисунок 3 – Схема до коммутации По закону Ома находим ток: i2(0-)=E/(r1+r2+r4)=95/46=2,07 А. По закону Ома находим напряжение: uC(0-)=i2(0-)·r4=2,07·12=24,78 В. По второму закону коммутации получим: uC(0)=uC(0-)=24,78 В. 3. Находим по закону Ома принужденную составляющую напряжения для схемы после коммутации ключа. r2 r3 r1 E uСnp Рисунок 4 – Схема цепи для принужденной составляющей Поскольку цепь разомкнута, то: uCпр=E =95 В. 4. Находим корень характеристического уравнения, которое получим через выражение для входного характеристического сопротивления Z(p). r2 r3 r1 1 Cp Z ( p) Рисунок 5 – Схема цепи для нахождения Z(p) Z(p)=r1+r2+r3+1/(Сp); Z(p)=0; т.е. r1+r2+r3+1/(Сp)=0; p=-1/((r1+r2+r3)·С)=-1/(48·45·10-6)=-462,96 c-1. 5. Определим закон изменения напряжения uC(t). uC(t)=uCпр+A·ep·t. Запишем уравнения для напряжения uC(t) в момент времени t=0. uC(0)=uCnp+A. Подставим численных значения: 24,78=95+A; A=-70,22. Запишем закон изменения напряжения uC(t): uC(t)=95-70,22·e-462,96·t В. Найдем ток через конденсатор: iC(t)=C·(d(uC(t))/dt)=C·p·A·ep·t=45·10-6·462,96·70,22=1,46·e-462,96·t А. 6. Построим графики переходного процесса uC(t) и iC(t). Найдем постоянную времени: τ=1/|p|=1/462,96=2,16 мс. Вычислим величину напряжения на конденсаторе uС(t) и тока через конденсатор iС(t) для моментов времени t=0, τ, 2τ, 3τ, 4τ, 5τ. uС(0)=95-70,22·e0 =24,78 В; uС(τ)=95-70,22·e-1=69,17 В; uС(2τ)=955-70,22·e-2=85,5 В; uС(3τ)=95-70,22·e-3=91,5 В; uС(4τ)=95-70,22·e-4=93,71 В; uС(5τ)=95-70,22·e-5=94,53 В. iС(0)=1,46·e0 =1,46 А; iС(τ)=1,46·e-1=0,54 А; iС(2τ)=1,46·e-2=0,2 А; -3 iaС(3τ)=1,46·e =0,07iCА; uC ( a) ( a) -4 iС(4τ)=1,46·e А; 0 24.78 =0,031.46 -3 69.17-5 0.54 i2.16·10 С(5τ)=1,46·e =0,01 А. 4.32·10 -3 85.5 0.2 6.48·10 -3 91.5 0.07 0.03 Построим графики переходного процесса uC(t) и iC(t) в программе Mathcad. 8.64·10 -3 93.71 0.01 94.53 0.01 100 90 80 70 60 uC( t) 50 40 30 20 10 0 0.0022 0.0043 0.0065 0.0086 0.0108 t Рисунок 6 – График напряжения на конденсаторе 1.6 1.4 1.2 1 iC( t) 0.8 0.6 0.4 0.2 0 0.0022 0.0043 0.0065 t Рисунок 7 – График тока в конденсаторе 0.0086 0.0108