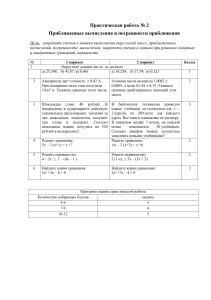
Входная контрольная работа по математике 11 класс 1 вариант 1 1. Вычислить: а) 1 − 54 ∙ 5 4 52 , 4 3 3 4 б) √ ∙ √6 . 4 4 2. Решите уравнение: 23𝑥+2 − 23𝑥−2 = 30. 3. Решите неравенство: log 8 (𝑥 2 − 4𝑥 + 3) < 1. 4. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания. 5. В правильной четырехугольной пирамиде сторона основания равна 6 см, высота 7 см. Найдите площадь поверхности пирамиды. 2 вариант 1. Вычислить: а) 102+√7 22+√7 ∙ 52+√7 3 , б) √11 1 4 3 1 ∶ √3 . 3 2. Решите уравнение: 16𝑥 − 17 ∙ 4𝑥 + 16 = 0. 3. Решите неравенство: log 0,2 (𝑥 2 − 5𝑥 + 7) < 0. 4. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 45°. Найдите площадь диагонального сечения параллелепипеда. 5. В правильной треугольной пирамиде сторона основания равна 4 см, а высота 6 см. Найдите площадь поверхности пирамиды. 3 вариант 7 1. Вычислить: а) 3 − 74 ∙ 7 4 72 , 3 б) √ 3 2 3 1 ∙ √2 . 4 2. Решите уравнение: 32𝑥−1 + 32𝑥 = 108 3. Решите неравенство: log 2 (𝑥 2 + 2𝑥) < 3. 4. В правильной треугольной призме длины всех ребер равны 2 см. Найдите площадь сечения, проведенного через боковое ребро и середину противолежащей стороны основания. 5. В правильной четырехугольной пирамиде боковое ребро равно 6√2 см и наклонено к основанию под углом 45°. Найдите площадь поверхности пирамиды. 4 вариант 1. Вычислить: а) 63+√5 23+√5 ∙ 33+√5 𝑥 𝑥 , 4 б) √15 5 8 4 2 :√ . 5 2. Решите уравнение: 64 − 8 − 56 = 0 3. Решите неравенство: lg(𝑥 2 − 8𝑥 + 13) > 0. 4. Основание прямой призмы – прямоугольный треугольник с катетами 6 см и 8 см. Диагональ боковой грани, содержащей гипотенузу, равна 26 см. Найдите высоту призмы. 5. В прямом параллелепипеде ABCDA1B1C1D1 𝐴𝐷 = 2, 𝐶𝐷 = 3, ∠𝐴𝐷𝐶 = 60°, A1C= √35. Найдите площадь поверхности параллелепипеда.