Цели - Virumaa Kolledž

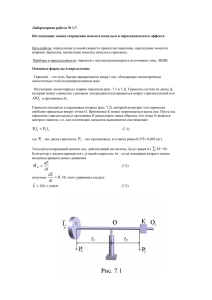
TTÜ VIRUMAA KOLLEDŽ
Tehniline füüsika
Reaalainete keskus
Üliõpilane:
Tehtud:
Õpperühm:
Arvestatud:
Töö nr. ja nimetus: № 5 Гироскоп с тремя степенями свободы
Цели:
1. Изучить понятие гироскопа
2. Определить момент инерции гироскопа
3. Определить скорость прецесси гироскопа
Приборы:
Рис 1. Установка эксперимента: (1 - маховик; 2 - нагрузка; 3 - дополнительные грузы; 4
- дополнительный штатив; 5 - крепеж; 6 - нить; 7 - секундомер; 8 - фотодатчик).
Теория и эксперимент:
Если тело привести во вращение относительно данной оси и оставить его вращаться, то
положение оси вращение изменится. Однако у каждого тела можно найти 3 оси,
положение
которых
не
меняется
при
вращении
относительно
них.
Это
перпендикулярные между собой оси (x, y, z), проходящие через центр тяжести тела.
3
Вращение относительно оси стабильное, если момент инерции максимальный или
минимальный. Вращение нестабильное если при малейшем наклоне ось теряет свою
стабильность. Например, вращение кольца на нити. Приводим кольцо во вращение и
оно сразу принимает горизонтальное положение (так как ось максимального момента
инерции совпадает с осью вращения).
Рис 2. Максимальный и минимальный момент инерции тонкого кольца при вращении
относительно свободных осей.
Тела, вращающиеся свободно, сохраняют свою ось вращение. Это явление используется
в гироскопах. Простейший гироскоп состоит колеса закрепленного на вал, которое
может вращаться свободно относительно вала.
С помощью следующего эксперимента определим момент инерции гироскопа. Для
этого соберем установку как показано на рисунке 3.
Рис 3. Установка экскперимента для определения момента инерции гироскопа
Из рисунка видно, что под действием груза диск гироскопа начинает вращаться,
появляется момент силы:
𝑀 = 𝐼𝜀, где 𝑀 - момент силы, 𝐼 - момент инерции гироскопа, 𝜀 - угловое ускорение
диска гироскопа.
𝑀
𝐼
=𝜀=
𝑑𝜔
𝑑𝑡
, 𝜔 - угловая скорость диска.
(1)
Так как момент силы - это произведение силы на плечо, то получим:
𝑀 = 𝐹𝑟 sin 𝛼, 𝐹 - равнодействующая силы, 𝑟 - плечо силы, то есть в данном случае
радиус барабана с ниткой. Угол 𝛼 = 900 .
Равнодействующая сила будет равна: 𝐹 = 𝑚𝑔 − 𝑚𝑎 = 𝑚(𝑔 − 𝑎).
(2)
В данном случае ускорение тангенсальное. Можно записать связь между линейным
ускорением и угловым ускорением: 𝜀 =
𝑎𝑡
𝑟
.
(3)
Так как система с грузом дивжется вниз с ускорением, то можно найти расстояние,
пройдённое грузом за данный промежуток времени (начальная скорость равна нулю):
ℎ=
𝑔𝑡 2
2
→ 𝑎𝑡 = 𝑔 =
2ℎ
𝑡2
(4)
Подставив 2,3,4 уравнения в 1, получим:
𝑀 𝐹𝑟 𝑚𝑟(𝑔 − 𝑎)
=
=
𝐼
𝐼
𝐼
𝑎 𝑚𝑟𝑔 − 𝑚𝑟𝑎
=
𝑟
𝐼
𝜀=
𝑎=
𝑚𝑟 2 𝑔
𝐼 + 𝑚𝑟 2
Тогда время равно:
𝑡2 =
2ℎ𝐼+2ℎ𝑚𝑟 2
𝑚𝑟 2 𝑔
(5)
I Ход работы:
Соберите установку как показано на рисунке 3. Выберете груз: 𝑚 = ...........гр = .........кг.
Измерьте радиус барабана с ниткой: 𝑟 = ...................... м.
Намотайте нить на барабан, а к концу нити закрепите груз. Для разных высот измерьте
время падения груза, заполните таблицу. Проведите 5 измерений. Момент инерции
определитe по формуле 5.
Номер опыта
Высота падения
Время падения
ℎ (м)
𝑡 (сек)
Время падения
2
𝑡 (сек )
2
Момент инерции
𝐼 (кг·м2)
1
2
3
4
5
𝐼1 =..................................................................................................................................
𝐼2 =..................................................................................................................................
𝐼3 =..................................................................................................................................
𝐼4 =..................................................................................................................................
𝐼5 =..................................................................................................................................
Определить среднее значение момента инерции и ошибку. Представить результат в
правильном виде (𝐼 ̅ ± ∆𝐼) кг·м2
Теоретический момент инерции определить с помощью соответствующей формулы из
теории. Сравнить полученный результат с измеренным. Написать вывод.
Теоретический момент инерции:
Вывод:
Тот же самый момент инерции определить из графика (угол наклона прямой линии).
построить график зависимости квадрата времени от высоты: 𝑡 2 = 𝑓(ℎ). В случае
сильного разброса точек используйте метод наименьших квадратов. График построить
либо на миллиметровой бумаге, либо с помощью соответствующего програмного
обеспечения.
II Ход работы:
Если гироскоп с помощью нити привести во вращение относительно горизонтальной
оси, то его вращение будет устойчивым. Если к концу вала прикрепить груз (то есть
будет действовать сила тяжести), то гироскоп начет вращаться оносительно
вертикальной оси (эта ось перпендикулярна вектору силы тяжести). Это явление
называется прецессией гироскопа. Установка эксперимента показана на рисунке 4.
Рис 4. Установка эксперимента для определения скорости прецессии гироскопа.
С помощью этого эксперимента можно определить скорость прецессии:
𝜔𝑝 =
𝑚𝑔𝑟
𝐼𝜔𝑟
,
(6)
где 𝑚 - масса дополнительного груза, 𝑟 - расстояние от точки опоры до груза (27 см), 𝐼 момент инерции гироскопа, 𝜔𝑟 - угловая скорость вращения диска гироскопа.
Последнее можно определить по формуле: 𝜔𝑟 =
𝜔р =
2𝜋
𝑡𝑝
2𝜋
𝑡𝑟
, где 𝑡𝑟 - время одного оборота диска.
, где 𝑡𝑝 - время одного оборота прецессии, 𝜔р - скорость прецесии. Если на
гироскоп не действует сила тяжести, то и нет прецессии, а также момент инерции
зависит от массы, то в формуле 6 масса сокращается. Получаем, что скорость прецессии
не зависит от массы. Если скорость вращения диска и скорость прецессии подставить в
формулу 6, то получим зависимость обратной величины продолжительности одного
оборота диска гироскопа от продолжительности оборото прецессии:
1
𝑡𝑟
=
𝑚𝑔𝑟 1
𝑡
4𝜋 2 𝐼 𝑝
(7)
По графику этой зависимости можно определить момент инерции гироскопа.
Определите это для двух разных масс. Нарисуйте графики зависимости
1
𝑡𝑟
= 𝑓(𝑡𝑝 ).
Графики построить либо на миллиметровой бумаге, либо с помощью соответствующего
програмного обеспечения. 𝑡𝑝 можно определить с помощью секундомера, а 𝑡𝑟 с
помощью фотобарьера. В конце работы напишите вывод.