На+дифракционную+решетку+длиной+l+и+периодом+d+падает+нормально

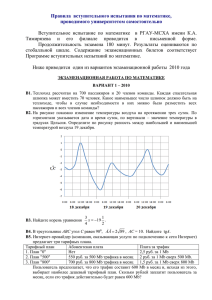
503. На дифракционную решетку длиной l и периодом d падает нормально
два монохроматических излучения с длинами волн λ1 и λ2. Дифракционная картина
наблюдается на экране расположенном в фокальной плоскости собирающей линзы,
находящейся за решеткой, расстояние между экраном и линзой равно L. Определить
полное число дифракционных максимумов для волн λ1 и λ2. Найти расстояние X12 на
экране между первым максимумом для волны λ1 и вторым максимумом для волны λ2.
Сможет ли решетка разрешить линии λ1 и λ2 в спектре первого порядка? Если нет, то
в спектре какого порядка возможно разрешение?
Дано:
l=18,0 мм=0,018 м
d=6∙10-6 м
L=1,2 м
λ1 =610∙10-9 м
λ2 =609,8∙10-9 м
k1=1
k2=2
Найти: N1, N2, x12, ∆λ, k
Решение:
1) Для волновых максимумов,
полученных
с
помощью
дифракционной
решетки,
справедливо соотношение
(1)
k  0,1, 2,3,...,
d sin k  k  ,
где d – постоянная решетки; k – угол отклонения лучей дифракционного максимума; k –
порядок максимума;  – длина волны.
Из соотношения (1) находим наибольший номер k или порядок высшего дифракционного
максимума, который может дать данная дифракционная решетка. Для этого предельный угол
дифракции должен быть равен

 max  , а sin  max  1 .
2
Поэтому
d sin  k
, или k  d .
(2)
k


Делаем расчет
k1 
6  10
6
6,1  10
7
 9,84 .
Так как k должно быть целым числом, то, следовательно, kmax1 = 9.
Общее число главных максимумов.,
учитывая центральный,
N1=2kmax1+1=2∙9+1=19
k1 
6  10
6
6, 098  10
7
 9,84 .
L
Так как k должно быть целым числом,
то, следовательно, kmax2 = 9.
Общее число главных максимумов,
учитывая центральный,
Х21
N2=2kmax2+1=2∙9+1=19
2) Из рисунка x2 , x1 - положение
дифракционного максимума на экране
для соответствующей длины волны.
Положение дифракционного максимума на экране для определенной длины волны
из рисунка:
x  L  tg , где L-расстояние от решетки до экрана, - угол дифракции, значение
которого определим из условия максимума на дифракционной решетке: d sin   k 
k
k
Отсюда sin 1  1 1 и sin 2  2 2 .
d
d
Координаты максимумов для каждого света x1  L  tg1 ,
x2  L  tg2
 sin 
 sin 2 sin 1 
sin 1
2

x21  x2  x1  L  tg2  tg1   L 


L


 1  sin 2 
1  sin 2 1
 cos 2 cos 1 
2



k2 2
k11
L
 

2
2
d
 k11 
 1   k2 2 
1 




 d 
 d 

Подставляем данные:



k2 2
k11



  L
2
2
2
d 2   k11 

 d   k2 2 












2  6, 098 107
6,1 10 7


x12  1, 2  


2
2
2
2
6
7
  6 106    2  6, 098 107 
6

10

6,1

10

 
 

 1, 2   0, 2076  0,1022   0,126 м  12, 6 см
3) Разрешающая способность дифракционной решетки

R
 kN ,

где  – минимальная разность длин волн двух спектральных линий  и +, разрешаемых
решеткой; k – порядок спектра; N – число щелей решетки.
l
Число щелей решетки N 
d
Для первого порядка R  2  3 103  6 103
 

kN

d
kl
;  
6,1107  6 106
 2, 033 1010 м=0,2033 нм
3
118 10
В нашем случае   1  2  610  609,8  0, 2 нм, следовательно, решетка не сможет
разрешить линии λ1 и λ2 в спектре первого порядка.
Определим, в спектре какого порядка возможно разрешение
d
d
6,1107  6 106
 
 k
; k
 1, 0167
kl
l
0, 2 109 18 103
Следовательно, k=2
Ответ: 1) N1=N2=19, 2) x12=12,6 см, 3) не сможет, 4) k=2