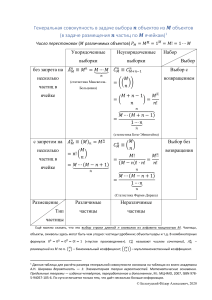
1 ЛОМОНОСОВСКИЕ ЧТЕНИЯ 2019 Стохастическая дозиметрия ионизирующего излучения, физика, техника измерений на космических аппаратах. Stochastic dosimetry of ionizing radiation, physics, measurement technique on spacecraft Анохин М.В.1, Галкин В.И.2 1-НИИЯФ МГУ, 2. ФИЗФАК МГУ С тех пор когда были введены в действие основные нормативные документы в области дозиметрии ионизирующего излучения на космических аппаратах минуло более четверти века. За это время очень существенно уточнились и теоретические и экспериментальные данные о процессах передачи энергии от ионизирующей частицы среде и последующих изменениях, происходящих в мишени. Эти знания были получены в первую очередь при отработке технологии изготовления микро и нано электронной техники, в которой чувствительные функциональные элементы создавались ионными пучками. Авторам этой работы стало ясно, что возникла необходимость уточнить содержание нормативных документов с учётом этих знаний. Существенным мотивом стали экспериментальные исследования частоты отказов электроники в штатных условиях эксплуатации проведённые рядом коллективов, в первую очередь на космических аппаратах SERVIS 1,2. Оказалось, что частота отказов, экспериментально измеренная в космических аппаратах иной раз отличается от предсказанной на основе действующих методик в тысячи раз. Исходное знание, конечно же незыблемо. При прохождении ионизирующих частиц через твердые тела энергия поглощается ядерным континуумом (NIEL) и электронами среды (IEL). При низких скоростях частиц доминирует NIEL. При больших скоростях доминирует IEL. Рис. 1. Ядерная S„ и электронная Se тормозные способности в зависимости от энергии имплантируемого иона. С учётом довольно известного и легко объяснимого факта – мягкого спектра поглощённой энергии космических лучей в материале спутников (рис.2) ясно, что вклад NIEL при оценке радиационной стойкости ЭРИ и при оценке вероятности выживания живой клетки должен быть рассмотрен. 2 Рис.2. The LET distributions using radiator CR-39 PNTDs and NAN-JAERI averaged over all phase 1-4 experiments (ISS). Plastic Nuclear Track Detectors (PNTDs) (ALTCRISS) project, Вместе с тем за эти годы знания уточнились существенно. Оказалось, возможным принципы макроскопической термодинамики применить к описанию нано размерных структур. Т. Хилл и многие другие показали, что нано термодинамика не только совместима с макроскопической, но и одновременно является её логическим продолжением. С учётом этих обстоятельств, для описания процессов, протекающих при взаимодействии заряженных частиц с материалом чувствительного объёма микроэлектроники в зоне трека логично использовать стохастическую гипотезу (теорию переноса Больцмана) [2]. Уравнением Больцмана определяется функция f(r, v, t), такая, что произведение f(r, v, t)d3rd3v есть поток атомов через элемент объема d3 r в точке r, движущихся со скоростью (v, d3v) в момент времени t. Исходят из того, что начальные условия для последующих столкновений определяются только функцией распределения f(r, v, t) и не зависят от предыдущих столкновений. В случае однокомпонентной среды уравнение Больцмана записывается в виде: ( d / dt v r (k/m) ) f (r, v, t) = K(v, v1; v’, v’’) d3 1 d3 , d3 , , |v v1| (f ‘ f ” – ff1) где K(v, v1; v’, v’’) d3 1 d3 , d3 , , — дифференциальное сечение рассеяния падающей частицы со скоростью v на атоме мишени, имеющем скорость v1, с переходом падающей частицы в интервал скоростей d3 , вблизи v’, а атома мишени — в интервал d3 , , вблизи v’’. При этом, f1 = f (r, v, t), f ‘= f(r, v’, t) и т.д., а k = ( r, v, t) есть внешняя сила, действующая на движущуюся частицу. 3 Для описания процесса в двухкомпонентной плазме, состоящей из электронов и ионов атомов среды , формирующейся в треке частицы, требуется добавление соответствующих индексов, что приводит к иерархии сцепленных уравнений, которые иногда могут быть расцеплены. Иногда это сделать не удаётся. Можно выделить два важных для нас предельных случая. Если мы хотим проследить только за падающими частицами, то движение частиц мишени не принимается во внимание и уравнение Больцмана принимает вид: - ( d / dt v r ) f (r, v, t) = N d3 , [ fK(v; v’) - , f ‘K(v’; v)] Здесь K(v; v’) d3 , , K(v; v’, v’’). Это уравнение может служить основным уравнением теории прохождения частиц через вещество. Наоборот, если важно знание состояния мишени, то уравнение Больцмана можно линеаризовать в случае относительно не плотного каскада столкновений, т. е. в случае, когда лишь небольшая доля атомов каскада приходит в движение. Тогда: f (r, v, t) = N (v) + F(r,v, t) , где -дельта-функция Дирака, N –плотность атомов мишени, F— «малая» добавка. В этом случае уравнение Больцмана принимает вид - ( d / dt v r ) F(r, v, t) = N d3 , d3 , , [ FK(v; v’, v”) - ’F’ K(v’; v, v”) - ’’F” K(v”; v’, v)] Здесь K(v; v’, v”) = K( , 0; ’, ”). Это уравнение может быть основным уравнением теории линейных каскадов столкновений в трекологии. Для конкретных задач используются различные формы уравнения переноса, как для «снаряда», так и для «мишени» при различном числе частиц мишени, участвующих в каскаде столкновений, профилей концентрации возникающих дефектов архитектуры кристаллов и концентрации остановившихся частиц – снарядов. Для полупроводников и диэлектриков энергия выводится из трека в основном по двум каналам: посредством акустических волн и теплопроводности фононным газом по решетке. Для процессов теплопроводности существует модель, описываемая системой неоднородных уравнений теплопроводности, в которой определяется температура электронного и ядерного континуума конденсированной среды (кристаллической решетки) с источниками. Чаще всего в монографиях, посвященных теории треков [3], для оценки состояния электронного и ядерного континуума конденсированной среды в зоне трека сильно ионизующей частицы используется система двух связанных уравнений теплопроводности в частных производных, отражающих представление о существовании двух подсистем, а именно электронов и решетки ионов, которые связаны электронфононным взаимодействием: 𝐶𝑒 𝜕𝑇𝑒 / 𝜕𝑡 = ∇(𝜆𝑒∇𝑇𝑒) − 𝑔(𝑇𝑒 − 𝑇𝑖) + 𝐴е(ze,𝑡) 𝐶𝑖 𝜕𝑇𝑖 / 𝜕𝑡 = ∇(𝜆𝑖∇𝑇𝑖) + 𝑔(𝑇𝑒 − 𝑇𝑖) + Аi (zi,𝑡), где 𝐶𝛾, 𝜆𝛾, 𝐴𝛾, 𝛾 = 𝑒, 𝑖 — соответственно теплоёмкости, теплопроводности и функции источников (плотность передаваемой мощности) для электронного газа и кристаллической решётки, 𝑔 — константа взаимодействия электронной подсистемы с решёткой, zγ – доза, полученная электронным и ионным континуумом в при прохождении одиночной частицы. Функции источников (сила осцилляторов) могут быть в принципе определена при известной из эксперимента удельной энергии, переданной электронной подсистеме - ze и удельной энергии, переданной решётке zi . Для некоторых случаев решения этих уравнений находят аналитически, в других случаях они решаются методом численного моделирования. 4 По нашей оценке, объёмная плотность мощности при остановке иона в области пика Брэгга составляет около 1012 Вт/см3. Для сравнения, объёмная плотность мощности при взрыве динамита 5х108 Вт/см3, объёмная плотность мощности теплового процесса ядерного взрыва – 1014 Вт/см3. Релаксация такого возбуждения может приводить к необычным структурным, фазовым и химическим превращениям облучаемого вещества в ближней окрестности траектории иона. Большинство же практических задач, связанных с прохождением заряженных частиц в веществе в области переноса, успешно решаются с помощью кодов SRIM и GEANT4 методом Монте-Карло. Важно, что метод не требует записи соответствующего уравнения переноса, фактически здесь нет проблем с формулировкой дискретной модели. В обоих случаях для реализации вычислительного алгоритма не требуется введение упрощений. Несомненное достоинство метода - возможность учета даже самых сложных геометрических границ. Результаты теоретического анализа: Рис. 3. The radial dose distribution around the track for of 4.8 GeV Fe-ion: calculated (open symbols), fitted (full curves) and the data of [15] (black points). Also shown are our previous (full curve) and our new calculations (open squares) for 50 MeV protons. Произошло и существенное усовершенствование техники измерений параметров поля ионизирующих частиц. В обиход вошли детекторы с высоким пространственным разрешением. Plastic Nuclear Track Detectors (PNTDs) CR-39, TLD. Получили распространение матрицы КМОП и МДП структур. 5 Рис.4. MEDIPIX: A Technology Developed at CERN, That Can Be Developed As An Active Real-time Space Radiation Dosimeter. 6 Рис.5. В эксперименте DAMIC используются ПЗС с высоким удельным сопротив- лением для поиска частиц темной материи. Энергетический порог ~ 50 эВ и отличное энергетическое и пространственное разрешение. Техника нашего исследования основана на применении композиции МДП матричных структур – полупроводниковых ионизационных камер ППИК (ПЗС). Матрица ПЗС представляет собой подложку из полупроводникового материала, на которую наносятся слой диэлектрика и система электродов. При подаче на электроды напряжения под ними в полупроводнике образуются потенциальные ямы для неосновных носителей (обедненные области). Потенциальные ямы под электродами разделены потенциальными барьерами. Совокупность потенциальных ям (ячеек) образует матрицу. Вводить заряд в ячейку можно термо- или фотогенерацией, а также за счет свободных носителей заряда, образуемых заряженными частицами. В нашем случае предметом исследования является третий эффект, первые два – фон. При подаче на электроды последовательности тактовых импульсов напряжения происходит управляемое перемещение зарядов, накопившихся в потенциальных ямах, вдоль полупроводниковой подложки в выходной регистр и далее в 7 выходное устройство. После прохождения частицы образовавшиеся носители диффузионно рассасываются и частично рекомбинируют. Основными функциями системы считывания информации с ППИК являются: усиление сигналов с возможно минимальным шумом перед преобразованием и фильтрацией аналогового сигнала (оптимизация соотношения сигнал/шум); запоминание и мультиплексирование; аналого-цифровое преобразование. Существенный вопрос электронного обеспечения ППИК - это мощностные ограничения, возникающие из-за малой пространственной области размещения первичной детекторной электроники. Схема устройства ППИК представлена на рисунке слева. На рисунке справа показан результат численного моделирования, проведённого нами при помощи кодов GEANT 4 остановки одиночного иона кремния в блоке из 361 ППИК. Цветовая шкала отградуирована в Греях. Используя блок из 2500 ППИК, расположенный в коронографе LASCO аппарата SOHO мы получили пространственное отображение величины удельной энергии поля ионизирующих частиц при экспозиции в несколько минут. Рисунок 6. Отображение величины удельной энергии поля ионизирующих частиц в блоке из 2500 ППИК в космическом аппарате SOHO во время солнечной вспышки. Цветовая шкала представлена в Грэях и откалибрована по треку минимально ионизирующей частицы (она пересекает рисунок в верхней части его). 8 Для проведения тестирования описанной методики исследования спектров плотности удельной энергии на космических аппаратах мы использовали ПЗС матрицы прибора LASCO (SOHO). На рисунке 5а приведена часть кадра размером 2.5 х 2.5 мм2 (Kodak KAI0340 CCD) во время солнечной вспышки «Бастилия». Оптический канал закрыт полностью крышкой. Слева показано 2D отображение распределения электрического заряда, накопленного вокселями матрицы за 18 секунд. Для анализа нами было отобрано около 5400 объектов, созданных ионизирующими частицами СКЛ около 5400 объектов, созданных ионизирующими частицами СКЛ из которых при превышении уровня дискриминации в 1 фКл 85% событий идентифицируется как локальный кластер. а) б) 2 Рисунок 7. Часть кадра размером 2, 5 х 2, 5 мм (Kodak KAI-0340 CCD) во время солнечной вспышки. Оптический канал закрыт полностью крышкой. Слева показано 2D отображение распределения электрического заряда, накопленного вокселями ПЗС матрицы за 18 секунд. Справа этот же участок кадра, обработанный макросом “gradient” (ImageJ, Int. 3D, Surf. Pl). По оси z отложена величина электрического заряда. Между эквипотенциальными (эквизарядовыми) уровнями шаг 0,1 фКл. Были отобраны одиночные события, происходящие под действием внешних радиационных факторов в структуре матричных оптически сенсоров и регистрируемых по характерным трековым изображениям на растровых кадрах видеосъёмки. Поиск интересующих нас объектов осуществляется по критериям в виде совокупности диапазонов яркости некоторого количества хронологически либо геометрически обособленных пикселей. Каждая такая совокупность является профилем идентификации, который формируется пользователем в диалоговом режиме и сохраняется под назначенным именем для возможности повторного поиска. Используются два типа профилей: кинетический и геометрический. К первому типу относятся профили, включающие диапазоны яркостей одного и того же пикселя для некоторого количества последовательно идущих смежных кадров. Особое условие, определяемое общим свойством всех регистрируемых событий, - превышение яркости в центральном кадре над яркостью в соседних кадрах. Предлагаемое, исследование является позитивным продолжением идеологемы, заложенной в действующем нормативном документе «МЕТОДИЧЕСКИЕ УКАЗАНИЯ МЕТОДИКИ РАСЧЕТА МИКРОДОЗИМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК КОСМИЧЕСКИХ ИЗЛУЧЕНИЙ. БЕЗОПАСНОСТЬ РАДИАЦИОННАЯ ЭКИПАЖА КОСМИЧЕСКОГО АППАРАТА В КОСМИЧЕСКОМ ПОЛЕТЕ. РД 50-25645.217-90». В этом документе заложено существенное положение о том, что при решении проблем радиационной стойкости чувствительного объёма малого размера необходимо знать энергию, выделяющуюся именно в этом объёме. При этом, существенной новизной в данном 9 проекте является уточнение физического понимания на базе современной теории трека тяжёлых заряженных частиц, введение новых представлений о механизме эволюции состояния вещества в пике Брэгга при остановке тяжёлой заряженной частицы и существенного усовершенствования техники дозиметрии с использованием достижений в технологии микро и нано электроники. Принято считать, что вероятность P(t) безотказной работы прибора убывает со временем за счет члена, пропорционального текущей средней частоте сбоев v(f) и за счет дополнительного члена, пропорционального среднему числу сбоев, произошедшему к текущему моменту времени, то изменение вероятности запишется как а вероятность примет вид где Средняя частота радиационных сбоев в приборе от потока F,(ϴ, Е, t) первичных частиц типа i в момент времени t где ϴ - направление первичной частицы; Е – ее энергия; ε – удельная энергия в ЧО поглощённая при прохождении частицы; w,(, Е,t) - спектр удельной энергии, создаваемый частицей типа i с энергией Е, летящей в направлении ϴ ; ω(ε ) - вероятность одиночного сбоя любого типа в ответ на появление ε достаточной величины. Первый интеграл берется по полусфере входящих частиц, а второй – по поверхности прибора. Если обозначить спектр удельной энергии, создаваемый в приборе потоком F/(ϴ, Е,t ), через тогда Ниже представлены спектры удельной энергии, полученные нами при обработке данных с КА STEREO. 10 Рис. 8. The specific energy frequency spectrum. Рис. 9. Specific energy dose spectrum. 11 При достаточно высоком значении энергии налетающей частицы происходит смещение атома мишени из равновесного (узлового) положения, что приводит к 12 возникновению междоузельного атома и вакансии (пары Френкеля). Образование дефектов продолжается, пока энергия окажется ниже пороговой энергии образо_ вания смещенного атома. В результате образуется определенное число дефектов Френкеля. Увеличение интенсивности облучающего потока ведет к более высо_ ким плотностям создаваемых дефектов, т.е., эффективность образования пар Френкеля возрастает. Приложение: На рис. 1 приведены результаты сравнительных испытаний микроэлектронных элементов на устойчивость к одиночным событиям, проведённых на пучке тяжёлых ионов, протонов и на круговой орбите, на высоте 1000 км. Репродукция из [2]. Рис. 1. Результат сравнительных испытаний микроэлектронных элементов на устойчивость к одиночным событиям, проведённых на пучке тяжёлых ионов, протонов и на круговой орбите, на высоте 1000 км 2. Space Environment Reliability Verification Integrated System Servis-1,2 [Электронный ресурс]. URL: de.academic.ru>. nsf/dewiki/2568726 (дата обращения 20.05.2018). ПРИЛОЖЕНИЕ 3. 13 Приложение 4 14 15 16 17 Приложение 5. 18 19 20 21 22 23 24 25 26 27 ν суммарная частота