Федеральное государственное бюджетное образовательное
учреждение высшего образования "МИРЭА - Российский
технологический университет"
Лабораторная работа № 1
«Основы алгоритмизации. Построение разветвляющихся
вычислительных процессов»
Выполнил:
Григорьев Дмитрий
КВБО-07-22
Москва 2022
Цель лабораторной работы:
Целью данной лабораторной работы освоить на практике
программирование разветвляющихся вычислительных процессов на
языке Си.
Описание работы:
В первом задании реализовано нахождение значение х по формуле
задания, а также реализован ввод значений t и z.
В втором задании представлено нахождение высот треугольника,
реализован ввод сторон с клавиатуры, проверка существования
треугольника, с данными сторонами и повторный ввод сторон, до
момента пока программа не будет досрочно завершена или не будут
введены значения сторон существующего треугольника. Далее
добавлен выбор искомой высоты по вершине, из которой она опущена
и проверка наличия такой высоты по принципу с существованием
треугольника, описанного выше. После чего идет нахождение искомой
высоты и вывод её длинны.
В третьем задании реализован ввод координат x, y и проверка на
нахождение их в нужной области. После чего выводится сообщение о
том, что точка лежит в области или не лежит.
В четвёртом задании производится поиск значений t и r, по вводимым
значениям x, y и представленной формуле, условия выбора формулы
также учтены в коде программы. Затем идёт вывод результата t и r.
Задание 1
Найти значение х по формуле и заданным значениям t и r, нахождение
значения y.
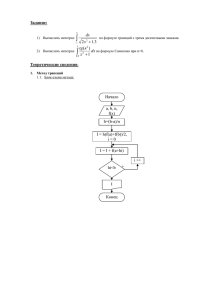
Алгоритм:
Реализация:
#include <stdio.h>
#include <math.h>
int main(void){
double t, z;
printf("Enter t > ");
scanf("%lf", &t);
printf("Enter z > ");
scanf("%lf", &z);
double y = (t + 2 * (1 / tan(z)));
double x = ((3 * y * y) / (4 * tan(z - 2 * t * t)));
printf("x = %6.5lf; y = %6.5lf; t = %6.5lf; z = %6.5lf;", x, y, t, z);
return 0;
}
Задание 2:
Наберите и выполните приведенную выше программу вычисления
высот треугольника по заданным сторонам.
Алгоритм задания:
Реализация программы:
#include <stdio.h>
#include <math.h>
double a, b, c, p, S;
char v;
int main(void) {
while (1){
get_sides();
if ((a + b > c) && (b + c > a) && (c + a > b)){
break;
}
else{
printf("There is no triangle with such sides\n");
printf("Enter the side lengths again\n");
continue;
}
}
printf("a = %6.3lf; b = %6.3lf; c = %6.3lf\n", a, b, c);
p = (a + b + c) / 2;
S = sqrt(p * (p - a) * (p - b) * (p - c));
while(1){
get_char();
if ((v == 'A') || (v == 'B') || (v == 'C')){
break;
}
else {
printf("Wrong vertex\n");
continue;
}
}
if (v == 'A'){
printf("Desired height = %6.3lf\n", (S / a) * 2);
}
if (v == 'B'){
printf("Desired height = %6.3lf\n", (S / b) * 2);
}
if (v == 'C'){
printf("Desired height = %6.3lf\n", (S / c) * 2);
}
return 0;
}
get_sides(){
printf("Enter the side length a > ");
scanf("%lf", &a);
printf("Enter the side length b > ");
scanf("%lf", &b);
printf("Enter the side length c > ");
scanf("%lf", &c);
}
get_char(){
printf("Enter the vertex from which the desired height comes out, A or B or C
> ");
scanf(" %c", &v);
}
Результаты работы программы:
Задание 3:
Написать программу, которая вводит координаты точки (x, y) и
определяет, попадает ли точка в заштрихованную область на рисунке,
который соответствует Вашему варианту. Попадание на границу
области считать попаданием в область.
Алгоритм:
Реализация программы:
#include <stdio.h>
int main(void){
double x, y;
printf("Enter the coordinate x > ");
scanf("%lf", &x);
printf("Enter the coordinate y > ");
scanf("%lf", &y);
printf("x = %6.3lf; y = %6.3lf\n", x, y);
if ((-1 <= x <= 1) && (-1 <= y <= 1) && (x * x + y * y >= 1)){
printf("The point falls into the area");
}
else{
printf("The point don't falls into the area");
}
return 0;
}
Результаты работы программы:
Задание 4:
Найти r и t.
Алгоритм:
Реализация программы:
#include <stdio.h>
#include <math.h>
int main(void){
double x, y, r, t;
printf("Enter the x > ");
scanf("%lf", &x);
printf("Enter the y > ");
scanf("%lf", &y);
if (x
r
}
else{
r
}
if (r
t
}
if (r
t
}
else{
t
}
> y){
= cos(x + y * y);
= log10((x + y) / (x - y));
< x){
= (x + r) / (cos(x - r));
== x){
= sqrt(y);
= fabs(x * x - r) / (1 + sin(r));
printf("x = %6.3lf; y = %6.3lf; r = %6.3lf; t = %6.3lf\n", x, y, r, t);
return 0;
}
Результат выполнения программы: