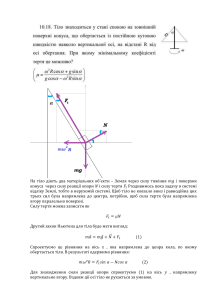
Практичне робота №1 за темою Векторний аналіз. Диференціальні оператори, що використовуються в механіці і фізиці. Теорема Гельмгольца. Мета роботи: ознайомлення із явним виглядом основних операторів векторного аналізу та їх застосуванні у механіці суцільного середовища. Оператор градієнту у декартових прямокутних координатах. grad i j k x y z Дивергенція (=розбіжність) векторного поля у декартових координатах. divF F Fx Fy Fz x y z Так, наприклад для поля швидкості, маємо: divV V Vx Vy Vz , x y z V Vx i Vy j Vz k Ротор векторного поля у декартових координатах i rotF F j k F Fy Fz Fx Fy Fx z i j k x y z z x z y y x Fx Fy Fz 2 2 2 Лапласіан або оператор Лапласу f 2 f f f f 2 2 2 x y z Обернена задача теорії поля: Щойно ми познайомились із основними операторами. Нагадаємо, що будь яке векторне поле (= або поле векторної величини) можна представити, згідно із теоремою Гельмгольца, як векторну суму градієнта деякого потенціального поля і ротора соліноідального поля: F A A 0 Так от, обернена задача полягає в тому, що знаючи дивергенцію та ротор деякої векторної величини, потрібно відтворити (= знайти) саму цю величину. Стосовно задач механіки рідини та газу, у якості невідомого поля слугує поле швидкості. Отже, задача зводиться до відшукання поля швидкості за відомими дивергенцією та ротором цієї швидкості. Звичайно, потрібно враховувати граничні умови задачі. Завдання додому: повторити тему “ Інтеграл із змінною верхньою межею ”. Іншими словами, як функція знаходиться за її похідною. Застосування теорем векторного аналізу (та теоретичної механіки ) до виводу рівнянь, що описують рух рідини та газу Застосування формули Остроградського. 1. Рівняння нерозривності. Нехай зміна густини за проміжок часу dt є dt . Тоді маса елементу об’єму тіла t змінюється на dtdV , а маса усього тіла на . dt dV t V t Така кількість рідини повинна протекти за проміжок часу dt крізь тіло. Змінивши знак, отримаємо кількість рідини, що витікає із назовню. Якщо віднести цю кількість до одиниці часу, то будемо мати: Q dV t V З іншого боку, зміну кількості рідини у даному об’ємі , можна порахувати через потік цієї рідини крізь поверхню, що її обмежує (поверхневий інтеграл другого роду) Q V ds S n Перетворивши, за формулою Остроградського, поверхневий інтеграл на об’ємний маємо: t V +div V dV 0 Оскільки ця рівність виконується для будь якої під області в межах усієї області, що розглядається, то із цього випливає диференціальне рівняння +div V 0 t яке носить назву рівняння нерозривності 2. Основне рівняння руху ідеальної (без урахування в’язкості) рідини. Нехай на рідину у загальному випадку діють як зовнішні сили, так і внутрішні. Вважаємо зовнішні сили пропорційні масі, так якщо F -- сила, що діє на одиницю маси, то на елемент рідини dV буде діяти сила dV F . Що стосується внутрішніх сил, тобто сил, що діють на виділений із рідини об’єм V з боку решти рідини, то ідеальна рідина характеризується саме тим, що ці сили приводяться до нормального, по відношенню до поверхні, тиску, що напрямлений усередину тіла (об’єму). Таким чином, на елемент поверхні dS діє, проекції котрої на вісі рівні: pdS cos , pdS cos , pdS cos де cos , cos , cos -- напрямні косинуси зовнішньої нормалі до поверхні. На все тіло (об’єм) буде діяти сила, що визначається проекціями p cos ds, p cos ds, p cos ds, S S S Або, якщо знову застосувати формулу Остроградського, p dV , x V p dV , y V p dV , z V Сила, що приходиться на елемент dV рідини, буде мати проекції p dV , p dV , p dV x y z І отже як вектор, представляється у вигляді dV grad p Якщо тепер за представити прискорення, що відповідає елементу законом Н’ютона dV a F dV dV gradp , то, за другим dV 1 a F gradp dt Це і є основне рівняння руху рідини у векторній формі. Звідки Завдання: отримати рівняння Ойлера Нав’є-Стокса. В класі. dV y V y V y V y V y dVx Vx Vx Vx Vx Vx V y Vz Vx V y Vz t x y z dt t x y z dt dVz Vz V V V Vx z V y z V z z t x y z dt dVx Vx V V V 1 p V x x V y x V z x F t x y z dt x x dV y V y V y V y V y 1 p Vx V y V z F t x y z dt y y dVz Vz V V V 1 p V x z V y z V z z F t x y z dt z z Рівняння Ойлера 2V 2V 2V Vx Vx Vx Vx 1 p x x x Vx V y Vz F t x y z x x x 2 y 2 z 2 2V 2V 2V V y V y V y V y y y y 1 p Vx V y V z F t x y z 2 y y x 2 y 2 z (1) (2) 2V 2V 2V Vz V V V 1 p z z z V x z V y z V z z F (3) t x y z 2 2 2 z z y z x V V V +div V 0 +div V x y z 0 t t t x y z (4) Рівняння (1-4) носять назву рівнянь Нав’є-Стокса і описують рух в’язкої як стисливої, так і нестисливої рідини.