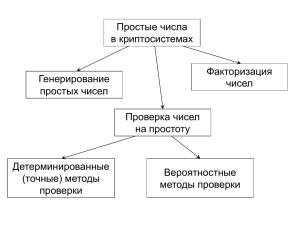
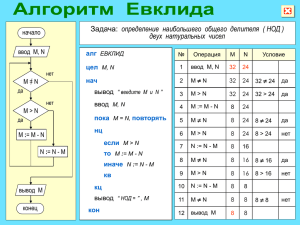
Арифметика целых чисел Множество целых чисел, обозначенных Z, содержит все числа (без дробей) от минус бесконечности до плюс бесконечности. Свойство 1: целое число 1 имеет только один делитель — само себя. Свойство 2: любое положительное целое число имеет по крайней мере два делителя — 1 и само себя (но может иметь больше). Одно целое число, часто необходимое в криптографии, — наибольший общий делитель двух положительных целых чисел. Два положительных целых числа могут иметь много общих делителей, но только один наибольший общий делитель. Например, общие делители чисел 12 и 140 есть 1, 2 и 4. Однако наибольший общий делитель — 4. Наибольший общий делитель двух положительных целых чисел — наибольшее целое число, которое делит оба целых числа. Алгоритм Евклида Факт 1: НОД (a, 0) = a Факт 2: НОД (a, b) = НОД (b, r), где r — остаток от деления a на b Первый факт говорит, что если второе целое число — 0, наибольший общий делитель равен первому числу. Второй факт позволяет нам изменять значение a на b, пока b не станет 0. НОД(36,10) = НОД(10,6) = НОД(6,4) = НОД(4,2) = НОД(2,0) Другими словами, НОД (36, 10) = 2, НОД (10, 6) = 2, и так далее. Это означает, что вместо вычисления НОД (36, 10) мы можем найти НОД (2, 0). Модульная арифметика Уравнение деления ( a=q*n + r ), имеет два входа ( a и n ) и два выхода ( q и r ). В модульной арифметике мы интересуемся только одним из выходов — остатком r. Мы не заботимся о частном q. Другими словами, когда мы делим a на n, мы интересуемся только тем, что значение остатка равно r. Это подразумевает, что мы можем представить изображение вышеупомянутого уравнения как бинарный оператор с двумя входами a и n и одним выходом r. Вышеупомянутый бинарный оператор назван оператором по модулю и обозначается как mod. Второй вход ( n ) назван модулем. Вывод r назван вычетом. Как показано на рисунке, оператор по модулю ( mod ) выбирает целое число ( a ) из множества Z и положительный модуль ( n ). Оператор определяет неотрицательный остаток ( r ). Мы можем сказать, что a mod n = r Разделим 27 на 5 - результат: r = 2. Это означает, что 27 mod 5 = 2. Разделим 36 на 12 — результат: r = 0. Это означает, что 36 mod 12 = 0. Свойства оператора mod Первое свойство: (a+b) mod n = [(a mod n +b mod n)] mod n Второе свойство: (a-b) mod n = [(a mod n - b mod n)] mod n Третье свойство: (a*b) mod n = [(a mod n * b mod n)] mod n Простые числа Асимметрично-ключевая криптография широко использует простые числа. Положительные целые числа могут быть разделены на три группы: число 1, простые числа и составные объекты. Положительное целое число — простое число тогда и только тогда, когда оно точно делимо без остатка на два целых числа — на 1 и на само себя. Составной объект — положительное целое число больше с чем двумя делителями. Простое число делимо без остатка только на себя и 1. Наименьшее простое число — 2, оно делится без остатка на 2 (само на себя) и 1. Обратите внимание, что целое число 1 — не простое число согласно определению, потому что простое число должно быть делимо без остатка двумя различными целыми числами, не больше и не меньше. Целое число 1 делимо без остатка только на себя; поэтому 1 — это не простое число. H(m)-1mod q = 9-1mod 11 = 5, a-1mod b = ab-2mod b 9-1mod 11 = 911-2mod 11= 99mod 11 =5 8-1 mod 17 = 817-2 mod 17 = 815 mod 17 5 –1 mod 23 = 523-2 mod 23 = 521 mod 23