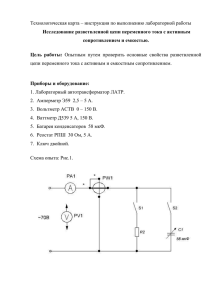
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра компьютерных систем в управлении и проектировании (КСУП) ОТЧЕТ По лабораторной работе № 3 по дисциплине «Моделирование систем управления» по теме «Решение дифференциального уравнения явным методом Эйлера» Выполнил: Студенты группы 518-2 ______________Щедрин А.А. «__» _______ 2021г. Профессор кафедры КСУП ____________Ганджа Т.В. «__» _______ 2021г. Томск 2021 2 Оглавление Введение ....................................................................................................................... 3 Ход работы ................................................................................................................... 4 Заключение .................................................................................................................. 4 3 Введение Целью данной лабораторной работы является расчет электрической цепи по методу компонентных цепей для сравнения результата с показаниями приборов в среде моделирования МАРС. Задачи: 1. Составить систему линейных алгебраических уравнений по методу компонентных цепей и рассчитать ее в системе Mathcad» по методу Гаусса для резистивного делителя, показанного на рисунке. 2.Собрать цепь резистивного делителя с помощью графического редактора среды моделирования МАРС и определить токи и напряжения схемы. Для этого в цепь установите три амперметра и два вольтметра. Сравнить с результатами расчета. 4 Ход работы Составим и рассчитаем характеристическое уравнение в системе Mathcad. Получаем, что С=4*10-6 – критическая точка, при которой дискриминант равен нулю. Результат представлен на рисунке 2.1. Рисунок 2.1 – Расчет в среде Mathcad Соберем в СМ МАРС последовательную RLC-цепь, параметризируем ее в соответствии с вариантом. Добавим в схему вольтметр и амперметр, и подключаем элемент «График» для того, чтобы подобрать значения емкости для получения апериодического и колебательного процессов. На рисунке 2.2 представлена схема, собранная в среде моделирования МАРС. Рисунок 2.2 – Схема, собранная в среде моделирования МАРС 5 В параметрах моделирования выбираем неявный метод Эйлера и запускаем схему. График переходного процесса при емкости равной 6 мкФ представлен на рисунке 2.3. Рисунок 2.3 – График переходного процесса при изначальном значении емкости Изменяя значение емкости получим апериодический процесс при С=100 мкФ. График апериодического переходного процесса представлен на рисунке 2.4. Рисунок 2.4 – График апериодического переходного процесса Изменим значение емкости для получения колебательного процесса. Получаем, что колебательный процесс достигается при значении емкости С=1000 нФ. График колебательного процесса представлен на рисунке 2.5. 6 Рисунок 2.5 – График колебательного переходного процесса 7 Заключение В ходе проведения лабораторной работы построили электрическую цепь в среде моделирования МАРС и, изменяя параметр емкости цепи, достигали различных переходных процессов. В итоге апериодический переходный процесс был достигнут при значении емкости 100 мкФ, а колебательный при значении емкости 1000 нФ.