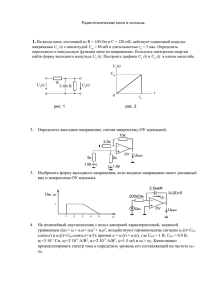
Лекция №17
Операционные усилители
Структура операционного усилителя
Помимо многочисленных самостоятельных приложений дифференциальный
каскад является основой современных УПТ и ОУ. Благодаря применению в нем
полевых или биполярных транзисторов, работающих в режиме микротоков,
удается обеспечить очень высокие входные сопротивления. Отсутствие
обратной связи по противофазному полезному сигналу позволяет получать
очень высокое усиление на каскад, малый дрейф нуля и дает возможность
подключать сигналы с инверсией и без нее. В силу этих свойств
дифференциальный каскад незаменим в схемотехнике ОУ.
Обобщенная структурная схема ОУ показана на рисунке.
Вых
Вх
1
3
4
5
1
2
3
4
5
Здесь:
и 2 - дифференциальные каскады в микротоковом и стандартном режиме,
- схема суммирования противофазных напряжений,
- схема сдвига уровня,
- выходной каскад.
Структура операционного усилителя
Получить высокое входное сопротивление от биполярных транзисторов,
изготовленных по стандартной технологии невозможно.
Хотя
h11э = (1…3) · τк / Cк + φ т · (1 + h21э) / Iэ,
но при уменьшении тока через транзистор ниже
1 мА происходит снижение его усиления h21э и
прироста входного сопротивления не
происходит. Решение задачи возможно при
использовании так называемых микротоковых
транзисторов с малыми допустимыми токами и
напряжениями. На входе операционного
усилителя сигнал мал и не требуется
обеспечивать большие предельно допустимые
напряжения и токи.
Второй способ увеличения входного сопротивления схемы – использование
полевых транзисторов. В этом случае не удается получить большое усиление
на каскад вследствие малой крутизны полевых транзисторов. Выход из данной
ситуации в использовании так называемой динамической нагрузки.
Динамическая нагрузка полевого транзистора
Известно, что динамическое сопротивление
биполярного транзистора гораздо больше
статического. Это означает, что для сигнала такой
транзистор будет обладать очень большим
сопротивлением, что даст возможность получить
большое усиление
K0 = S R0 .
В то же время режим транзистора по постоянному
току будет определяться малым статическим
сопротивлением, что не приведет на нем к слишком
большому падению питающего напряжения и позволит
создать оптимальный режим работы.
Еще один способ повышения входного сопротивления первого каскада –
использование составных транзисторов, включенных по схеме Дарлингтона на
микротоковых транзисторах.
Не следует забывать, что все эти методы увеличения входного
сопротивления ОУ сопряжены с повышением постоянной времени первого
каскада и, как следствие с ухудшением воспроизведения высоких частот.
Поэтому ОУ используется для усиления сравнительно низкочастотных сигналов.
Структура операционного усилителя
Разумеется, в зависимости от схемы конкретного ОУ, некоторые каскады
могут отсутствовать или объединяться по функциям.
+Е
R1 R2
VT1
Один из возможных вариантов схемы суммирования
противофазных напряжений в упрощенном виде
показан на рисунке.
Схема практически одинаково нагружает выходные
транзисторы предыдущего каскада и дает возможность
перейти от двухпроводной схемы передачи сигналов к
однопроводной (относительно общего провода).
Особенностью работы транзистора VT1 совместно с резисторами R1 и R2
является то, что он служит только для инвертирования сигнала и имеет
единичное усиление. В результате оба сигнала на выходе VT1 оказываются в
фазе и складываются.
На выходе схемы суммирования даже в отсутствие сигналов обычно
имеется постоянный (+1. 5 В...+2. 5 В) потенциал, не дающий возможность
получить нулевое напряжение на выходе ОУ. Для устранения этого недостатка
в схему приходится включать схему сдвига уровня.
Структура операционного усилителя
В этой схеме за счет действия генератора тока I0 на
+Е
резисторе R получают требуемое падение напряжения.
В качестве оконечных каскадов ОУ целесообразно
VT1
использовать схемы, обладающие низким выходным
сопротивлением, например, эмиттерный повторитель или
R
двухтактный эмиттерный повторитель на комплементарных
транзисторах.
Операционный усилитель является универсальным средством
= I0
схемотехники, с помощью которого и при наличии
соответствующих внешних элементов достигается
разнообразие вариантов использования.
Стремление получить большой коэффициент усиления ОУ К = S R0 за счет
увеличения сопротивлений нагрузки дифференциальных каскадов, которые и
обеспечивают основное усиление, приводит к увеличению постоянных
времени этих каскадов и, как результат, к ухудшению воспроизведения
высоких частот. Это, а также условие обеспечения устойчивости ОУ при
применении любой, в том числе и 100% обратной связи приводит к заданию
особой формы амплитудно-частотной и фазо-частотной характеристики. Фаза
выходного напряжения не должна доходить до 1800. Поэтому частоты среза
двух каскадов должны быть как можно дальше отнесены друг относительно
друга.
Амплитудно-частотная характеристика операционного усилителя
Поэтому частота среза одного
из каскадов лежит в области 10
…100 Гц, а второго – на частотах 2
… 4 МГц. На частоте первого среза
фаза равна 450, а за ней не
превышает -900, на частоте
второго среза фаза приобретает
набег – 135о, но при этом
усиление уже меньше единицы,
благодаря чему самовозбуждения
ОУ не возникает даже при 100%
отрицательной обратной связи.
Включения операционного усилителя
На базе операционных усилителей реализуются различные устройства
обработки сигналов.
Все многообразие схемных решений на основе ОУ базируется на двух
типах включения: инвертирующем и неинвертирующем.
Анализ схем с операционными усилителями принято проводить, пользуясь
следующими допущениями:
- так как входное сопротивление ОУ очень велико, то можно пренебречь
током, протекающим в его входной цепи;
- из-за очень большого коэффициента усиления напряжение между
инвертирующим и неинвертирующим входами настолько мало, что им можно
пренебречь.
Неинвертирующее включение ОУ
Пользуясь этими допущениями, проанализируем параметры базовых схем.
Z2
Z1
DA1
Uвх
Uвых
При неинвертируещем включении ОУ входной
сигнал усиливается без изменения фазы.
Сопротивления Z1 и Z2 передают часть выходного
напряжения во входную цепь в виде сигнала
отрицательной обратной связи.
При этом, так как напряжение между входами
ОУ близко к нулю, можно считать, что к Z1
приложено напряжение, равное Uвх, а к сумме
сопротивлений Z1 + Z2 – напряжение Uвых.
Тогда
Uвх = Uвых Z1 / (Z1 + Z2).
Отсюда
K = Uвых / Uвх = 1 + Z2 / Z1.
Входное и выходное сопротивления схемы определяются свойствами
самого ОУ.
Инвертирующее включение ОУ
Iос
Iвх
Z1
Uвх
Z2
DA1
Uвых
Инвертирующий усилитель изменяет фазу
входного сигнала на противоположную. Так как
неинвертирующий вход соединен с общим
проводом и напряжение между входами очень
мало, то можно считать, что все входное
напряжение падает на сопротивлении Z1, а все
выходное напряжение приложено к Z2.
Из-за высокого входного сопротивления ОУ на его вход практически не
будет ответвляться часть тока Iвх. Поэтому можно считать, что
Iвх = Iос = Uвх / Z1 = Uвых / Z2.
Тогда
K = Uвых / Uвх = Z2 / Z1
и
Rвх = Uвх / Iвх = Z1.
Выходное сопротивление схемы мало и определяется параметрами самого
ОУ.
На основе базовых схем могут быть построены различные по назначению
устройства.
Сумматор и вычитатель сигналов
U1
R1 I1
U2
R2 I2
R0 I0
U3
R3 I3
DA1
Uвых
Инвертирующий сумматор позволяет
осуществить эффективное суммирование
множества сигналов.
Пусть требуется просуммировать три
сигнала.
Для этого, учитывая принятые допущения,
можно записать
I1 + I2 + I3 = I0.
Но I1 = U1 / R1, I2 = U2 / R2, I3 = U3 / R3, I0 = Uвых / R0.
Отсюда
Uвых = (U1 R0 / R1 + U2 R0 / R2 + U3 R0 / R3).
Пусть R0 = R1 = R2 = R3 , тогда
Uвых = (U1 + U2 + U3).
Таким образом, выходное напряжение равно сумме входных напряжений.
R0 I0
На аналогичном принципе, учитывая инверсию
U1 R1 I1
сигнала с одного из входов ОУ, можно построить
DA1
вычитатель двух сигналов.
U2 R2 I2
Uвых
Интегратор и дифференциатор
Iос
Uвх R Iвх
C
DA1
Uвых
Если в схеме инвертирующего усилителя
элементом обратной связи служит конденсатор С,
то можно записать
Iвх = Iос = Uвх / R = Uвых j C.
Коэффициент передачи устройства в
операторной форме
K(p) = 1 / (pR C) = 1 / (p ).
Тогда Uвых = Uвх(p) / (p ). Делению изображения на оператор p во
временной области соответствует интегрирование оригинала. Переходя от
изображения к оригиналам, получаем
Uвых(t) = Uвх(t)dt.
Значит, рассмотренная схема может служить интегратором.
Поменяем местами в предыдущей схеме резистор
Iос R
и конденсатор. Тогда аналогично будем иметь
Uвх j C = Uвых / R.
Uвх С Iвх
K(p) = p R C = p .
DA1
Uвых(p) = p Uвх(p) .
Перейдем к временной записи
Uвых
Uвых(t) = dUвх(t)/dt.
Значит, исследуемое устройство дифференцирует
входной сигнал.
Логарифмирующий усилитель
Iос
Uвх R Iвх
VD1
DA1
Uвых
Рассмотрим работу ОУ, охваченного
нелинейной обратной связью, где в качестве
нелинейного элемента используется p-n переход.
Его вольтамперная характеристика описывается
выражением
i = I [eU/(m × т) 1] ,
где т - температурный потенциал,
m - коэффициент, связанный с поверхностной рекомбинацией (для
кремниевого диода m = 1...1. 3) ,
I - начальный ток диода.
Рассуждая аналогично вышесказанному, получим
Uвх / R = I { exp[ Uвых / (m т)] 1}.
При больших отрицательных амплитудах выходных сигналов
exp[ Uвых / (m т)] >> 1 .
Тогда
Uвых/( m т ) ln[Uвх / (IR)]
и
Uвых = 2,3m т lg[Uвх/(IR)] .
Следовательно, устройство логарифмирует входной положительный сигнал.
Антилогарифмирующий усилитель и перемножитель сигналов
Iос
UвхVD1 Iвх
R
DA1
Uвых
X
Путем изменения подключения диода и
резистора в схеме, имеем антилогарифмирующий
усилитель.
lgUвых = Uвх/( 2.3m т ) + lg(IR).
Используя логарифмирующий и
антилогарифмирующий усилители, можно
осуществить, например, операцию перемножения
двух положительных сигналов
lg(X)
lg
XY
Y
lg
lg(Y)
alog
Рассмотренными выше
устройствами далеко не
исчерпываются возможные
применения операционных
усилителей. На базе ОУ строятся
другие арифметические устройства,
фазовращатели, активные RCфильтры, компараторы, генераторы,
некоторые разновидности
импульсных схем.
Активные фильтры
Активный фильтр представляет собой четырехполюсник, содержащий
пассивные RС-цепи и активные элементы: транзисторы, электронные лампы
или операционные усилители. Активные фильтры обычно не содержат катушек
индуктивности. Стремление исключить катушки индуктивности из фильтра
вызвано рядом причин: 1) катушки индуктивности имеют большие габариты и
массу; 2) потери в катушках приводят к отклонению расчетных характеристик
фильтра от реальных значений; 3) в катушках рассеивается большая мощность;
4) в катушках с сердечником проявляется нелинейный эффект, связанный с
насыщением сердечника. Активные фильтры можно реализовать на
повторителях напряжения, на операционных усилителях, на усилителях с
ограниченным усилением и др.
Пассивные частотные фильтры выполняются на LC- или на RС-цепях без
применения усилительных активных элементов. Такие фильтры не требуют
источников питания и имеют простое исполнение, однако они не обеспечивают
хорошего разделения полосы пропускания от полосы затухания; в области
пропускания и затухания. Moгут наблюдаться большие неравномерности
передаточной характеристики; очень сложно выполнить условие согласование
фильтра с нагрузкой.
В отличие от пассивных, активные фильтры обеспечивают более
качественное разделение полос пропускания и затухания. В них сравнительно
просто можно регулировать неравномерности частотной характеристики в
области пропускания и затухания, не предъявляется жестких требований к
согласованию нагрузки с фильтром. Все эти преимущества активных фильтров
обеспечили им самое широкое применение.
Активные фильтры
На базе операционных усилителей реализуются активные фильтры,
предназначенные для частотного разделения или выделения сигналов.
В большинстве случаев электрический фильтр представляет собой
частотно-избирательное устройство. Следовательно, он пропускает сигналы
определенных частот и задерживает или ослабляет сигналы других частот.
Наиболее общими типами частотно-избирательных фильтров являются
фильтры нижних частот (которые пропускают низкие частоты и задерживают
высокие частоты), фильтры верхних частот (которые пропускают высокие
частоты и задерживают низкие частоты), полосно-пропускающие фильтры
(которые пропускают полосу частот и задерживают те частоты, которые
расположены выше и ниже этой полосы) и полосно-заграждающие фильтры
(которые задерживают полосу частот и пропускают частоты, расположенные
выше и ниже этой полосы).
Более точно характеристику частотно-избирательного фильтра можно
описать, рассмотрев его передаточную функцию
H(s) = V2(s) / V1(s).
Величины V1 и V2 представляют собой
соответственно входное и выходное напряжения,
как показано на общем изображении фильтра.
Активные фильтры
Для установившейся частоты s = jω (j = √ — 1) передаточную функцию
можно переписать в виде
Н (jω) = | Н (jω) | e jφ(ω)
где | Н (jω) | — модуль передаточной функции или амплитудно-частотная
характеристика; e jφ(ω) — фазо-частотная характеристика, а частота ω (рад/с)
связана с частотой f (Гц) соотношением ω = 2πf.
Диапазоны или полосы частот, в которых
сигналы проходят, называются полосами
пропускания и в них значение амплитудночастотной характеристики | Н (jω) |
относительно велико, а в идеальном случае
постоянно. Диапазоны частот, в которых
сигналы подавляются, образуют полосы
задерживания и в них значение амплитудночастотной характеристики относительно мало,
а в идеальном случае равно нулю.
На рисунке штриховой линией показана амплитудно-частотная
характеристика идеального фильтра нижних частот с единственной полосой
пропускания 0<ω<ωс и полосой задерживания ω>ωс. Частота ωс между двумя
этими полосами определяется как частота среза.
Активные фильтры
На практике невозможно реализовать эту идеальную характеристику,
поскольку требуется сформировать очень узкую переходную область.
Следовательно, основная проблема при конструировании фильтра заключается
в приближении реализованной в лаборатории реальной характеристики с
заданной степенью точности к идеальной. Вариант такой реальной
характеристики показан сплошной линией на том же рисунке.
В практическом случае полосы пропускания и задерживания четко не
разграничены и должны быть формально определены. Исходя из нашего
определения в качестве полосы пропускания выбирается диапазон частот, где
значение амплитудно-частотной характеристики превышает некоторое заранее
выбранное число, обозначенное на рисунке как А1, а полосу задерживания
образует диапазон частот, в котором амплитудно-частотная характеристика
меньше определенного значения, например, А2. Интервал частот, в котором
характеристика постоянно спадает, переходя от полосы пропускания к полосе
задержания, называется переходной областью. Приведенный выше
практический пример имеет полосу пропускания 0<ω<ωс, полосу задерживания
ω>ω1 и переходную область ωc<ω<ω1.
В основном затухание в полосе пропускания никогда не превышает 3 дБ.
Таким образом, из приведенного примера следует, что значение амплитудночастотной характеристики в полосе пропускания составляет по крайней мере
1/√2 =0,707, или 70,7 % ее максимального значения. В этом случае можно
также сказать, что в полосе пропускания амплитудно-частотная характеристика
на 3 дБ ниже или меньше максимального значения.
Активные фильтры
Существует много способов построения фильтра с заданной передаточной
функцией n-го порядка. Один популярный способ заключается в том, чтобы
представить передаточную функцию в виде произведения сомножителей Н1
Н2, ..., Нn и создать схемы или звенья, или каскады N1, N2, ... Nm,
соответствующие каждому сомножителю. Наконец, эти звенья соединяются
между собой каскадно (выход первого является входом второго и т. д.). Если
эти звенья не влияют друг на друга и не изменяют собственные передаточные
функции, то общая схема обладает требуемой передаточной функцией n-го
порядка. ОУ обладает бесконечным входным и нулевым выходным
сопротивлениями. Таким образом, его можно использовать для реализации
невзаимодействующих звеньев.
Для фильтров первого порядка передаточная функция представляется в
виде
V2 / V1 = P(s) / (s + C),
С — постоянное число, a P(s) — полином первой или нулевой степени. Для
фильтров второго порядка передаточная функция
V2 / V1 = P(s) / (s2 + Bs + C)
где В и С—постоянные числа, a p(s) — полином второй или меньшей степени.
Для четного порядка n>2 обычная каскадная схема содержит n/2 звеньев
второго порядка, каждое со своей передаточной функцией, которую мы
рассмотрели. Если же порядок n>2 является нечетным, то схема содержит
(n—1)/2 звеньев второго порядка со своими передаточными функциями.
Активные фильтры
Наличие полюсов и нулей в фильтре определяет величину параметров
фильтра и, следовательно, вид частотной характеристики. Например,
положение полюсов обеспечивает минимальное изменение частотной
характеристики (максимальную плоскостность) в полосе пропускания. Такие
фильтры называются фильтрами Баттерворта.
Для разработчиков очень важно знать особенности частотных
характеристик фильтров различной конфигурации. Они приведены в таблице.
Активные фильтры
Тип
частотной
характеристики
Фильтр
Баттерворта
Особенности
Максимально плоская частотная характеристика в полосе
пропускания, равномерное увеличение подавления в полосе
затухания, нелинейное изменение фазы от частоты (неравномерная
задержка)
Фильтр Чебышева Увеличение коэффициента усиления на предельной частоте,
неравномерность в полосе пропускания и в полосе затухания
Фильтр Бесселя Самые лучшие импульсные показатели (время нарастания и время
(или Томпсона) отсечки), линейное изменение фазы (равномерная задержка)
Эллиптический
фильтр
(или Кауэра)
Полюсы находятся в полосе подавления, что обеспечивает выброс на
предельной частоте и пульсации в полосе пропускания и в полосе
затухания, но самый лучший наклон характеристики
Параболический Самый лучший компромисс между частотной характеристикой и
фильтр
временными показателями
Активные фильтры
На рисунке показаны
сравнительные амплитудночастотные характеристики
различных типов активных
фильтров третьего порядка.
Активные фильтры
Существуют разные конструкции активных фильтров, каждый из которых
используется для того, чтобы в качестве характеристики фильтра получить
нужную функцию, как, например, функции Баттерворта, Чебышева и т. д.
Каждая схемная реализация является наилучшей в смысле тех или иных
желательных свойств, и поэтому «абсолютно лучшей» схемы активного фильтра
не существует.
Некоторые свойства, желательные для схемы фильтра таковы, а) малое число
элементов, как активных, так и пассивных; б) легкость регулировки; в) малое
влияние разброса параметров элементов, в особенности значений емкостей
конденсаторов; г) отсутствие жестких требований к применяемому
операционному усилителю, в особенности требований к скорости нарастания,
ширине полосы пропускания и полному выходному сопротивлению; д)
возможность создания высококачественных фильтров; е) чувствительность
характеристик фильтр, по отношению к параметрам элементов и коэффициенту
усиления ОУ (в частности к произведению коэффициента усиления на ширину
полосы пропускания) или частоте среза fср. Последнее свойство - одно из
наиболее важных по многим причинам. Фильтры, требующие соблюдения
высокой точности значений параметров элементов, трудно настраивать, и по
мере старения элементов настройка теряется; дополнительной неприятностью
является требование использовать элементы с малым допуском значений
параметров. Схема с управляемым источником напряжения (УИН) обязана своей
популярностью в основном своей простоте и малому числу деталей, но эта схема
страдает некоторым недостатком - высокой чувствительностью к изменениям
значений параметров элементов.
Активные фильтры
В качестве
примера рассмотрим
различные
исполнения
низкочастотного
активного фильтра
Баттерворта второго
порядка. При одной и
той же амплитудночастотной и фазочастотной
характеристике
исполнение может
быть самым
различным.
Активные фильтры
Схема Салена-Кея
Схема Тоу-Томаса
Схема MFB
Схема Фишера-Тоу
Активные фильтры
Схема KHN
Схема Тоу-Томаса 2
Схема Эскера-Моссберга
Активные фильтры верхних частот
Фильтр Баттерворта второго порядка
Фильтр Чебышева второго порядка
Полосовой фильтр Баттерворта
Полосовой фильтр Чебышева
Полосно-заграждающий фильтр Баттерворта
Полосно-заграждающий фильтр Чебышева