Цель работы: сравнить практические результаты измерения импеданса для различных цепей с теорией.
Приборы и материалы: Осциллограф (0,025%), вольтметр (±0,254 В), резистор, конденсатор, катушка
индуктивности.
1. Теория
Под двухполюсником понимается электрическая цепь, состоящая из некоторого числа элементов и имеющая
два контакта. Соответственно под четырехполюсником понимается цепь, имеющая 4-е контакта (2-а входных и 2-а
выходных).
В данной этой работе рассматриваются лишь линейные n-полюсники. Особенностью линейных n-полюсников
является то, что их поведение описывается линейным дифференциальным.
1.1
Общие понятия и некоторые полезные соотношения
Представление напряжений и токов, комплексные амплитуды, импеданс. При подключении n-полюсников за счет
внешнего генератора на входных клеммах возникает напряжение, которое в дальнейшем будет записываться как
uin, а через n-полюсник течет ток i. Считая, что все эти величины гармонические запишем:
u = U*exp {j(ω − ϕu )};
i = I*exp {j(ω − ϕi )};
Этим значениям u, i соответствуют комплексные амплитуды:
(1)
(2)
Uc = U* exp(−j*ϕu);
Ic = I* exp(−j*ϕi);
(3)
(4)
Их отношение называется комплексным импедансом:
Zc =
𝑈𝑐
𝐼𝑐
=
𝑈
𝐼
∗ exp{ 𝑗(𝜙𝑖 − 𝜙𝑢 )} = 𝑧 ∗ exp{𝜙}
(5)
Это и есть основная характеристика 2-полюсника.
Основной характеристикой четырехполюсника является комплексная величина, называемая коэффициентом
передачи:
̇
𝑈
𝐾̇ = 𝑈вых
= 𝐾𝑒 𝑗𝜑 , где К- амплитудная ,
̇
вх
2
𝜑 -фазовая характеристики
(6).
1.2
Рассмотрение простейших двухполюсников
В настоящей работе мы рассматриваем 4-е типа двухполюсников:
Рис. 1: Типы исследуемых двухполюсников
Необходимо отметить что мы включали двухполюсники следующим образом: сигнал с генератора мы подавали
как и показано на рисунке на клеммы по "краям" двухполюсника, а сигнал снимали, сравнивая напряжение на
клемме, соединенной с резистором и клемме, "между" активным элементом и этим резистором.
Двухполюсник А. Zsum = ZR + ZC = R +
|𝑍| =
√(𝑅𝜔𝐶)2 +1
𝜔𝐶
1
j𝜔C
=R−j
1
(7)
𝜔C
1
)
𝑅𝜔𝐶
arg(𝑍) = −𝑎𝑟𝑐𝑡𝑔(
(8), (9)
Двухполюсник B. Zsum = ZR + ZL = R + j𝜔𝐿
|𝑍| = √(𝜔𝐿)2 + 𝑅 2
(10)
𝜔𝐿
arg(𝑍) = 𝑎𝑟𝑐𝑡𝑔( )
(11), (12)
𝑅
Двухполюсник С. Этот двухполюсник является модификацией двухполюсника А.
𝑍Z
c R
Zsum = ZR + Z +Z
= R(1 +
c
1−j𝜔𝑅𝐶
2
)
R
(𝜔𝑅𝐶 ) +1
1
𝜔𝑅𝐶
|𝑧| = 𝑅√(1 + (𝜔𝑅𝐶)2 +1)2 + ((𝜔𝑅𝐶)2 +1)2
𝜔𝑅𝐶
arg(𝑍) = −𝑎𝑟𝑐𝑡𝑔(
)
(𝜔𝑅𝐶)2 + 2
(13)
(14)
(15)
Двухполюсник D. Этот двухполюсник является "гибридом" двухполюсников B и С:
𝑍 Z
Zsum = ZR + Z L+ZR = R(1 +
L
|𝑧| = 𝑅√(1 +
R
𝜔𝑅𝐿
)2
(𝐿𝜔)2 +𝑅2
(𝐿𝜔)2 +j𝜔𝑅𝐿
)
(𝐿𝜔)2 +𝑅2
(𝐿𝜔)2
+ ((𝐿𝜔)2 +𝑅2 )2
(𝑅𝐿𝜔)
)
2(𝐿𝜔)2 +𝑅2
arg(𝑍) = 𝑎𝑟𝑐𝑡𝑔(
3
(16)
(17)
(18).
1.3
Простейшие четырехполюсники
В этой схеме мы рассматриваем два четырехполюсника: мостовой четырехполюсник и так называемый тройной
RC фазовращатель.
Мостовой четырехполюсник. При этом предполагается, что C1 = C2 = C и
R1 = R2 = R, в таком случае токи по обеим веткам совпадают. Согласно
векторным диаграммам импеданса этот четырехполюсник обладает
свойством не изменять амплитуду сигнала, но сдвигать его на некоторый
угол ϕ, который определяется как:
𝜙
𝑈𝑅
2
𝑈𝐶
𝑡𝑔 ( ) =
= 𝜔𝑅𝐶
(19)
При этом сдвиг фазы может изменяться в пределах ϕ ∈ [0; π) и сдвигу в π
соответствует ωRC → +∞, что невозможно. Поэтому для получения более
существенных сдвигов фазы используют тройной RC фазовращатель.
Тройной RC фазовращатель. Эта схема позволяет значительно сдвигать
фазу выходного сигнала, однако также уменьшает амплитуду.
Ω = 𝜔𝑅𝐶; 𝐾(𝜔) =
𝜙=
Рис. 4: Схема тройного RC
фазовращателя
4
3𝜋
2
Ω3
√(1−6Ω2 )2 +Ω2 (5−Ω)2
− 𝑎𝑟𝑐𝑡𝑔(
Ω(5−Ω)2
)
1−6Ω2
(20)
(21)
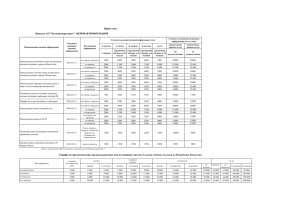
2. Практическая часть.
В этом задании ищем зависимость импеданса и сдвига фазы в линейном двухполюснике от
частоты входного напряжения.
Двухполюсник №1.
2Uвх,
В
26,6
2OG,
В
10,3
ω, Гц
|Z|,
кОм
100
2Uвых,
В
12
100
28,8167
100
1,03201
200
18
26,6
12,2
200
19,2111
200
0,74474
300
21,2
26,6
11,6
300
16,3113
300
0,57898
400
22,6
26,2
10,4
400
15,0708
400
0,47819
600
23,8
26
7,6
600
14,2017
600
0,32502
800
24,4
25,8
6
800
13,7459
800
0,24845
1500
25,8
26,2
3,92
1500
13,2016
1500 0,15253
2000
25,6
26,2
2,4
2000
13,3047
2000 0,09389
2500
25,6
26,2
2,16
2500
13,3047
2500 0,08448
3000
25,6
26,2
1,68
3000
13,3047
3000 0,06567
4000
25,8
26,2
1,22
4000
13,2016
4000
6000
25,8
26
1,02
6000
13,1008
6000 0,03955
8000
25,8
26
0,52
8000
13,1008
8000 0,02016
ω, Гц
arg(Z),
0,0473
|Z|
35
30
25
20
15
10
5
0
100 200 300 400 600 800 1500 2000 2500 3000 4000 6000 8000
5
ω, Гц
arg(Z)
1,2
1
0,8
0,6
0,4
0,2
0
100 200 300 400 600 800 1500 2000 2500 3000 4000 6000 8000
Двухполюсник 2
2Uвх,
В
25,8
2OG,
В
0
ω, Гц
|Z|,
кОм
100
2Uвых,
В
25,2
100
13,3095
100
0
400
24,6
25,8
1,24
400
13,6341
400
0,05043
700
24,4
25,8
2
700
13,7459
700
0,08206
1000
24,2
25,8
3,12
1000
13,8595
1000
0,12929
1200
24,4
26,2
3,84
1200
13,959
1200
0,15803
1400
24,4
26,2
4
1400
13,959
1400
0,16468
1600
24,4
26,2
4,8
1600
13,959
1600
0,19801
2000
24,4
26,2
5,76
2000
13,959
2000
0,23831
2500
24,2
26,2
7,36
2500
14,0744
2500
0,30903
3000
23,6
26,2
8,2
3000
14,4322
3000
0,35486
4000
22,8
26,2
10,2
4000
14,9386
4000
0,46382
5000
21,8
26,2
11,8
5000
15,6239
5000
0,57196
6000
20,4
26,2
13
6000
16,6961
6000
0,69093
7000
19,2
26,2
13,4
7000
17,7396
7000
0,77248
8000
18
26,2
13,8
8000
18,9222
8000
0,87363
10000
16
26,2
13,6
10000
21,2875
10000 1,01599
ω, Гц
6
ω, Гц arg(Z),
ω, Гц
|Z|,
25
20
15
10
5
0
ω, Гц
arg(Z),
1,2
1
0,8
0,6
0,4
0,2
0
100
400
700 1000 1200 1400 1600 2000 2500 3000 4000 5000 6000 7000 8000 10000
2.1 Двухполюсник 3
7
ω, Гц
2Uвх,
В
26,2
2OG,
В
3,2
ω, Гц
|Z|
кОм
ω, Гц
arg(Z),
рад
100
2Uвых,
В
15,2
100
22,4079
100
0,21211
150
16
26,2
4,08
150
21,2875
150
0,25785
200
17,2
26,2
4,88
200
19,8023
200
0,28767
300
18,8
26,2
5,76
300
18,117
300
0,31139
500
21,4
26,2
5,92
500
15,9159
500
0,28029
650
22,6
25,8
5,36
650
14,8407
650
0,23945
800
23,4
25,8
4,8
800
14,3333
800
0,20659
1500
24,8
26
3,12
1500
13,629
1500
0,12614
2000
25,4
26
2,6
2000
13,3071
2000
0,10254
3000
25,6
26
1,8
3000
13,2031
3000
0,07037
4000
25,6
26
1,24
4000
13,2031
4000
0,04846
7000
25,6
26
0
7000
13,2031
7000
0
ω, Гц
|Z|
25
20
15
10
5
0
100
150
200
300
500
650
800 1500 2000 3000 4000 7000
8
ω, Гц
arg(Z)
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
100
150
200
300
500
650
800 1500 2000 3000 4000 7000
9
ω, Гц
Двухполюсник 4
2Uвх,
В
25,8
2OG,
В
0
ω, Гц
|Z|,
кОм
100
2Uвых,
В
25,4
100
13,2047
100
0
500
24,4
25,8
1,44
500
13,7459
500
0,05905
800
24,2
25,8
2,12
800
13,8595
800
0,08772
1500
24,2
26,2
3,68
1500
14,0744
1500
0,15266
2000
23,2
26,2
4,6
2000
14,681
2000
0,1996
2500
22,4
26,2
5,2
2500
15,2054
2500
0,23428
3000
21,6
26,2
5,76
3000
15,7685
3000
0,26993
4000
20,2
26,2
6
4000
16,8614
4000
0,30158
5000
19,4
26,2
6,04
5000
17,5567
5000
0,3166
7000
17,6
26,2
5,6
7000
19,3523
7000
0,32381
8000
16,8
26,2
5,2
8000
20,2738
8000
0,31469
10000
16
26,2
4,88
10000
21,2875
10000 0,30994
ω, Гц
ω, Гц arg(Z), рад
(Z|
25
20
15
10
5
0
100
500
800 1500 2000 2500 3000 4000 5000 7000 8000 10000
1
0
ω, Гц
arg(Z),
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
100
500
800 1500 2000 2500 3000 4000 5000 7000 8000 10000
ω, Гц
2.5.1 Четырехполюсник A
В этом задании определяем зависимость фазовой
характеристики четырехполюсника от частоты при
постоянном сопротивлении нагрузки, и от сопротивления
нагрузки при постоянной частоте(100 гц).
При R=140 кОм
При
φ, рад ω=73
Гц
ω, Гц
2OG, В
2OF, В
10
1,02
12,2
15
1,92
12,4
0,0837 R, кОм 2OG, В 2OF, В φ, рад
0,15546
0
0,62
12,3 0,05043
20
4,16
12,6
0,33647
10
1,08
12,3
0,08792
25
6,16
12,7
0,50641
20
2,96
12,3
0,24304
30
7,6
12,7
0,64153
30
4,32
12,3
0,35887
40
10
12,8
0,89667
40
5,76
12,3
0,48736
50
11,4
12,8
1,09872
50
7,28
12,2
0,63941
60
12,4
13
1,26579
60
8,48
12,2
0,76853
73
13,1
13,1
1,5708
70
9,52
12,2
0,89519
1
1
100
12,4
13,1
1,89918
80
10,1
12,2
0,9753
150
10,5
13,2
2,22184
90
10,8
12,2
1,08702
200
8,56
13,2
2,436
100
11,2
12,2
1,16309
250
7,12
13,2
2,57188
110
11,6
12,2
1,25587
300
6,08
13,1
2,65895
120
11,8
12,2
1,31402
400
4,72
13,1
2,773
130
12
12,2
1,38948
600
3,1
13,2
2,90453
140
12,2
12,2
1,5708
850
2,08
13,2
2,98336
1000
1,84
13,2
3,00174
1500
1
12,2
3,05953
2500
0,4
12,3
3,10907
3000
0
12,3
3,14159
φ
3,5
3
2,5
2
1,5
1
0,5
3000
2500
1500
1000
850
600
400
300
250
200
150
100
73
60
50
40
30
25
20
15
10
0
ω
φ
1,8
1,6
1,4
1,2
1
0,8
0,6
0,4
0,2
0
0
10
20
30
40
50
60
70
80
1
2
90 100 110 120 130 140
R
2.5.1 Четырехполюсник B
На данном графике представлена
экспериментальная зависимость фазовой характеристики RC
моста, изображенного на рис.4 от частоты
входного
напряжения.
ω, Гц
2OG, В 2OF, В
60 100 200
300
400
500
700
1000
2000
3000
4000
6000
8000
10000
30000
-
φ, рад
2,14
3,86
3,14159
3,14159
2,48 2,10061
3,96 1,79601
5,16
6,12
7,32
7,76
6,4
4,72
3,6
2,52
1,82
1,56
0
5,16
6,36
8,16
9,68
12,1
12,8
13
13
13,2
13,2
13,3
1,5708
1,2952
1,11307
0,93006
0,55733
0,37766
0,28059
0,19508
0,13832
0,11846
0
1
3
φ
3,5
3
2,5
2
1,5
1
0,5
0
ω
3. Вывод
Мы исследовали двух- и четырехполюсники, сняв зависимость сдвиг фазы от частоты поданного
сигнала. Также для всех двухполюсников была снята зависимость величины импеданса от
частоты. Для всех двухполюсников полученные опытным путём результаты почти полностью
совпали с теорией.
1
4