сопромат

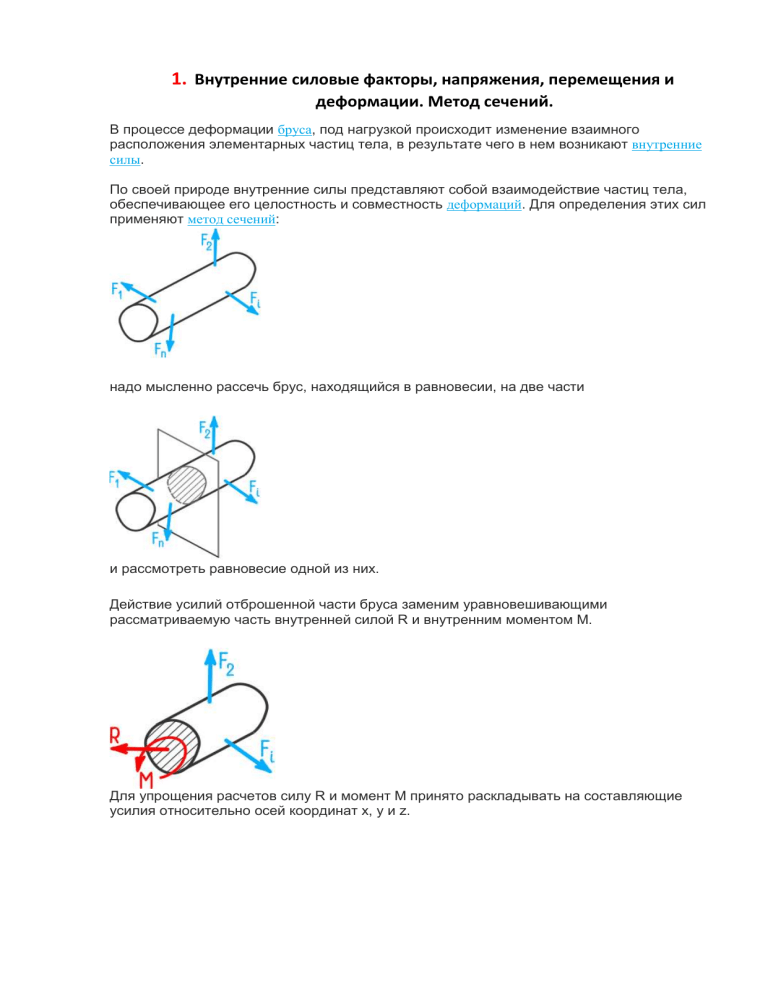
1. Внутренние силовые факторы, напряжения, перемещения и
деформации. Метод сечений.
В процессе деформации бруса, под нагрузкой происходит изменение взаимного
расположения элементарных частиц тела, в результате чего в нем возникают внутренние
силы.
По своей природе внутренние силы представляют собой взаимодействие частиц тела,
обеспечивающее его целостность и совместность деформаций. Для определения этих сил
применяют метод сечений:
надо мысленно рассечь брус, находящийся в равновесии, на две части
и рассмотреть равновесие одной из них.
Действие усилий отброшенной части бруса заменим уравновешивающими
рассматриваемую часть внутренней силой R и внутренним моментом M.
Для упрощения расчетов силу R и момент M принято раскладывать на составляющие
усилия относительно осей координат x, y и z.
Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут
возникать следующие внутренние силовые факторы:
 Nz = N — продольная растягивающая (сжимающая) сила;
 Mz = T — крутящий (скручивающий) момент;
 Qx (Qy) = Q — поперечные силы;
 Mx (My) = M — изгибающие моменты.
Каждый внутренний силовой фактор определяется из соответствующего уравнения
равновесия оставшейся после рассечения бруса части (уравнения статики):
2. ЗАКОН ГУКА
Законом Гука называют базовую зависимость в механике, устанавливающую
взаимосвязь между усилиями и соответствующими им упругими деформациями.
Закон был открыт в 1660 году английским ученым Робертом Гуком.
Проведя серию экспериментов с растяжением и сжатием пружин, Гук заметил, что
изменение их длины прямо пропорционально растягивающей (сжимающей) их
силе.
Свои наблюдения он оформил в виде закона: «Какова сила, таково и удлинение».
Современная формулировка закона существенно отличается от оригинала и
зависит от дисциплины, в которой рассматривается зависимость деформаций от
усилий.
Подробнее про закон Гука смотрите в нашем видео:
Закон Гука в сопромате
В технической механике и сопротивлении материалов в частности закон Гука
гласит: «До определенного момента, называемого пределом пропорциональности,
упругие деформации прямо пропорциональны напряжениям».
Здесь:
σ — Нормальные напряжения в сечении;
ε — Относительные продольные деформации.
Рассмотрим преобразование физической формы закона к его механическому виду.
Подставим вместо коэффициента k его выражение
Отношение продольной силы F к площади поперечного сечения A в левой части
дает нормальные напряжения в сечении
Отношение абсолютных деформаций к начальной длине образца –
это относительное изменение его длины
В таком виде закон Гука используется в сопромате и технической механике.
При растяжении и сжатии
При растяжении и сжатии закон Гука можно получить, вернув в его канонический
вид геометрические параметры стержня (длину и площадь поперечного сечения), и
записав получившееся выражение относительно линейной деформации:
Здесь
Δl- Абсолютная деформация стержня;
F — Продольная сила;
l — Длина стержня до нагружения;
E – Модуль продольной упругости материала;
A – Площадь поперечного сечения стержня.
При изгибе
При изгибе закон устанавливает зависимость между кривизной продольной оси и
величиной изгибающего момента в соответствующем сечении балки.
где:
ρ — Радиус кривизны продольной оси балки в данном сечении;
M — Величина соответствующего внутреннего изгибающего момента;
E – Модуль Юнга;
Ix — Осевой момент инерции поперечного сечения балки.
Обобщенный закон Гука
Для общего случая нагружения изотропных материалов, когда напряженное
состояние отличается от линейного (одноосного) применяется
закон Гука в обобщённом виде.
ε — Относительные деформации вдоль соответствующих осей;
ν — Коэффициент Пуассона;
σ — Нормальные напряжения по соответствующим площадкам элемента.
Определяется отношением относительных поперечных εпоп и
продольных εпр деформаций бруса
Потому что деформации в поперечных направлениях тоже влияют на изменение
продольных размеров.
Для чистого сдвига
γ — Угловое перемещение соответствующей площадки элемента;
τ — Касательные напряжения;
G — Модуль упругости II рода (модуль сдвига).
3. Потенциальная энергия упругих материалов при
растяжении и сжатии.
УСЛОВИЕ ПРОЧНОСТИ ПРИ РАСТЯЖЕНИИСЖАТИИ
При продольном осевом нагружении (растяжении-сжатии) в поперечных
сечениях бруса имеют место только нормальные напряжения σ. Поэтому для
обеспечения прочности стержней и стержневых систем достаточно выполнение
условия:
Здесь
σ
– максимальные расчетные нормальные напряжения в стержне,
N – внутренние продольные силы (принимаются с построенных эпюр),
А – соответствующая площадь поперечного сечения бруса,
[σ] – допустимые напряжения (расчетное сопротивление) для материала стержня,
max
Условие прочности при чистом изгибе:
Условие жесткости
Условие жесткости стержня
условию жесткости:
ПОПЕРЕЧНАЯ СИЛА И ИЗГИБАЮЩИЙ МОМЕНТ
Поперечным изгибом называется такой вид деформирования бруса, при
котором внешние нагрузки действуют перпендикулярно к его продольной
оси. Деформация изгиба заключается в искривлении оси бруса.
Брус с прямой осью, работающий на изгиб, называется балкой. Если плоскость
действия внешних нагрузок проходит через ось балки и одну из главных
центральных осей поперечного сечения, изгиб называется прямым. В этом случае
ось балки искривляется в плоскости действия нагрузок и является плоской кривой.
В сечениях балки возникают два внутренних силовых фактора: изгибающий
момент Мх и поперечная сила Qy
4. Устойчивость. Критическая нагрузка.
Критическая сила
вычисляется по формуле Эйлера:
μ – коэффициент приведенной длины или коэффициент приведения