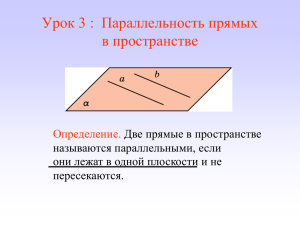
АКСИОМЫ СТЕРЕОМЕТРИИ. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ Цель данного теста — проверить, умеет ли ученик: − применять аксиомы стереометрии и следствия из них для обоснования взаимного расположения прямых и плоскостей в пространстве; − различать параллельные, скрещивающиеся и пересекающиеся прямые с помощью признаков, приведенных в условии; − использовать определение и признак параллельности прямых в пространстве для обоснования взаимного расположения прямых в пространстве. Вариант 1 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) Точки А и В принадлежат плоскости α, а точка С лежит вне плоскости α. Выберите правильное утверждение. А. Прямая АС лежит в плоскости α. Б. Прямая СВ лежит в плоскости α. В. Прямая АВ лежит вне плоскости α. Г. Прямая АВ лежит в плоскости α. 2. (0,5 б.) На рисунке изображена пирамида SABC. Выберите правильное утверждение. A. Прямая ВС является общей прямой плоскостей SBC и ABC. Б. Прямая АВ является общей прямой плоскостей ABC и SBC. B. Плоскости ABC и ASC пересекаются по прямой АВ. Г. Плоскости ASB и ASC пересекаются по прямой ВС. 3. (0,5 б.) Параллелограмм ABCD и треугольник ABS не лежат в одной плоскости, MN — средняя линия треугольника ABS. Выберите правильное утверждение. A. Прямые M N Б. Прямые M N B. Прямые M N Г. Прямые M N и DC параллельны. и DC скрещивающиеся. и DC пересекаются. и DC не лежат в одной плоскости. 4. (1 б.) В пространстве даны три точки А, В, С, которые лежат на одной прямой. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Через точки А, В, С можно провести только одну плоскость. Б. Через точки А, В, С можно провести бесконечное множество разных плоскостей. B. Через точки А и В можно провести плоскость, которая не содержит точку С. Г. Через точку А можно провести плоскость, которая имеет с прямой ВС только одну общую точку. 5. (1 б.) В кубе АBCDA1B1C1D1 построено сечение плоскостью, которая проходит через точки А, В1, D1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Сечением является прямоугольный треугольник. Б. Сечением является правильный треугольник. B. Прямая B1D1 принадлежит секущей плоскости и плоскости грани A1B1C1D1. Г. Секущая плоскость и плоскость грани АВСD имеют только одну общую точку А. 6. (1 б.) В пространстве даны две разные прямые а и b, которые лежат в плоскости α. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые а и b могут пересекаться. Б. Прямые а и b могут быть параллельными. B. Прямые а и b могут быть скрещивающимися. Г. Через прямые а и b можно провести плоскость, отличную от плоскости α. 7. (2 б.) В пространстве дана плоскость α и точка А. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если некоторая прямая, которая проходит через точку А, пересекает плоскость α, то точка А обязательно лежит в плоскости α. Б. Если некоторая прямая, которая проходит через точку А, лежит в плоскости α, то точка А лежит в плоскости α. B. Любая прямая, которая проходит через точку А, обязательно пересекает плоскость а. Г. Любая прямая, которая проходит через точку А, обязательно лежит в плоскости α. 8. (2 б.) В кубе АВСDA1B1C1D1 построено сечение плоскостью, которая проходит через точки В, D, К, где точка К — середина ребра СС1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Сечением является правильный треугольник. Б. Сечением является равнобедренный треугольник. B. Прямая ВК пересекает плоскость грани А1B1C1D1. Г. Прямые ВD и B1D1 параллельны. 9. В пространстве даны две параллельные прямые a и b и некоторая прямая с. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если прямая с пересекает прямую a, то она обязательно пересекает и прямую b. Б. Если прямая с пересекает обе прямые а и b, то прямые a, b, с лежат в одной плоскости. B. Если прямые a и c скрещивающиеся и прямые b и с также скрещивающиеся, то прямая с обязательно пересекает плоскость, содержащую прямые а и b. Г. Если прямая с пересекает прямую a и не пересекает прямую b, то прямые b и с обязательно скрещивающиеся. 10. (3 б.) Точки А, В, С, D не лежат в одной плоскости. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Продолжения сторон АВ и CD пространственного четырехугольника ABCD пересекаются. Б. Прямые АС и BD могут пересекаться. B. Три точки из данных четырёх точек могут лежать на одной прямой. Г. Можно провести только три разные плоскости, каждая из которых проходит через три из четырех данных точек. 11. (3 б.) В пирамиде SABC, все ребра которой равны, проведено сечение плоскостью, которая проходит через точки К, L, М, лежащие на ребрах AS, АС, ВС, причем АК = 2KS, AL = 2LC, СМ = 2МВ. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Секущая плоскость и прямая S C имеют общую точку. Б. Сечением является трапеция. B. Прямая M L пересекает плоскость ABS в точке, которая является общей точкой прямых AВ и ML . Г. Три плоскости: секущая плоскость и плоскости AB C и A BS имеют одну общую точку. 12. (3 б.) Точки А, В, С, D не лежат в одной плоскости; точки К, L, М, N — середины отрезков АD, DС, ВС, АВ соответственно. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые КМ и LM могут быть скрещивающимися. Б. Прямые КN и LM могут пересекаться. B. Точка пересечения прямых МК и NL лежит на прямой, которая проходит через середины отрезков ВD и АС. Г. Если АС = ВD, то прямые КМ и LN пересекаются под острым углом. Вариант 2 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) В пространстве даны две прямые а и b, которые пересекаются в точке А. Выберите правильное утверждение. A. Через прямые a и b можно провести две разные плоскости. Б. Через прямые а и b можно провести только одну плоскость. B. Через прямые а и b можно провести бесконечное множество плоскостей. Г. Через прямые a и b нельзя провести плоскость. 2. (0,5 б.) На рисунке изображен прямоугольный параллелепипед АВСDA1B1C1D1. Выберите правильное утверждение. A. Плоскость ABC не совпадает с плоскостью грани ABCD. Б. Плоскости ABC и BB1C пересекаются по прямой АС. B. Плоскости АBС и BB1C1 пересекаются по прямой ВС. Г. Прямая АВ является общей прямой плоскостей A1AD и В1ВС. 3. (0,5 б.) Параллелограммы АВСD и ABC1D1 не лежат в одной плоскости. Выберите правильное утверждение. A. Прямые D1С1 и DС не лежат в одной плоскости. Б. Прямые D1С1 и DС пересекаются. B. Прямые D1С1 и DС параллельны. Г. Прямые D1С1 и DС скрещивающиеся. 4. (0,5 б.) В пространстве дана прямая а и точка А на ней. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Через точку А можно провести плоскость, которая пересекает прямую а . Б. Через прямую а и точку А можно провести бесконечное множество разных плоскостей. B. Если плоскость проходит через точку А, то она обязательно содержит прямую а . Г. Через прямую а и точку А можно провести только одну плоскость. 5. (1 б.) В кубе АВ СD A 1 B 1 C 1 D 1 построено сечение плоскостью, которая проходит через точки А, С , К, где точка К - середина ребра ВВ 1 . Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Сечением является равносторонний треугольник. Б. Точка В лежит в секущей плоскости. B. Прямая АС принадлежит секущей плоскости и плоскости АВD. Г. Секущая плоскость пересекает прямую ВВ1 в точке К. 6. (1 б.) В пространстве даны четыре точки А, В, С, D. Известно, что прямые АВ и СD — скрещивающиеся. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые АС и ВВ могут быть параллельными. Б. Прямые АВ и ВС лежат в одной плоскости. B. Прямые АО и ВС могут пересекаться. Г. Три точки из данных четырёх точек могут лежать на одной прямой. 7. (2 б.) В пространстве даны три различные точки А, В, С. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если АВ = 3 см, ВС = 4 см, АС = 5 см, то точки А, В, С не лежат на одной прямой. Б. Если АВ = 3 см, ВС = 4 см, АС = 7 см, то через точку А, В, С можно провести только одну плоскость. B. При любом размещении точек А, В, С через них можно провести бесконечное множество разных плоскостей. Г. При любом размещении точек А, В, С через них можно провести плоскость. 8. (2 б.) В кубе АВСDA1B1C1D1 построено сечение плоскостью, которая проходит через точки К, L, М — середины ребер АВ, АD, АА1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Сечением является прямоугольный треугольник. Б. Сечением является правильный треугольник. В. Прямая КL пересекает плоскость ВСС 1 в точке, которая является точкой пересечения прямых КL и ВС. Г. Секущая плоскость имеет общие точки с плоскостью DDC1. 9. (2 б.) В пространстве даны две различные прямые a и b, которые пересекаются, и некоторая прямая с. Отметьте, какие из следующих четырех утверждений правильные, а какие – неправильные. A. Если прямая с пересекает обе прямые а и b , то прямые а, b ,с могут лежать в одной плоскости. Б. Если прямая с параллельна прямой а и пересекает прямую b , то прямые а , b ,с обязательно лежат в одной плоскости. B. Прямая с может быть параллельной как прямой а , так и прямой b . Г. Если прямая с параллельна прямой а , то прямые а , b ,с обязательно лежат в одной плоскости. 10. (3 б.) В пространстве даны четыре разные точки А, В , С , D. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если прямые АВ и СD пересекаются, то прямые АС и ВD лежат в одной плоскости. Б. Если прямые АD и ВС пересекаются, то прямые АВ и СD обязательно пересекаются. B. Диагонали АС и ВD четырехугольника АВСD обязательно пересекаются. Г. Если прямые АС и ВD не пересекаются, то данные точки лежат в одной плоскости. 11. (3 б.) В пирамиде S A B C , все ребра которой равны, проведено сечение плоскостью, которая проходит через точки К , L , М , лежащие на ребрах S C , S A , С В , причем S C = 4 K S , С В = 4 M B , A S = A A L . Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Секущая плоскость и плоскость AB C имеют общую точку, которая лежит на прямой пересечения секущей плоскости и плоскости ACS . Б. Сечением является равнобокая трапеция. B. Прямая K L пересекает плоскость AB C в точке пересечения прямых КL и АВ. Г. Прямая KL пересекает плоскость АBС в точке пересечения прямых АС и MN . 12. (3 б.) Точки А , В , С , D не лежат в одной плоскости; точки К , L , М , N — середины отрезков A D , D C , В С , А В соответственно. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая, которая проходит через середины отрезков АС и BD, и прямая КМ скрещивающиеся. Б. Если К М = L N, то L K N = 60°. B. ЕСЛИ АС > BD, то K N > K L. Г. ЕСЛИ АС < BD, то K N > K L. Вариант 3 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) Прямая а лежит в плоскости α, a точка А лежит вне плоскости α. Выберите правильное утверждение. A. Прямая а имеет только две общие точки с плоскостью α. Б. Каждая точка прямой а принадлежит плоскости α. B. Точка А принадлежит прямой а. Г. Через прямую а и точку А можно провести две разных плоскости. 2. (0,5 б.) На рисунке изображен прямоугольный параллелепипед ABCDA1B1C1D1. Выберите правильное утверждение. A. Плоскости ABC и А1С1В1 пересекаются по прямой AA1. Б. Плоскости ADD1 и DCC1 пересекаются по прямой АС1. B. Прямая DD1 является общей прямой плоскостей BCC1и A DD 1 . Г. Прямая DC1 пересекает плоскость ABC. 3. (0,5 б.) Трапеции АВСD и АВ М N с общим основанием АВ не лежат в одной плоскости. Выберите правильное утверждение. A. Прямые МN и DС пересекаются. Б. Прямые МN и DС параллельны. B. Прямые МN и DС скрещивающиеся. Г. Прямые МN и DС не лежат в одной плоскости. 4. (1 б.) В пространстве дана плоскость α и точка В вне её. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Через точку В можно провести бесконечное множество прямых, которые пересекают плоскость α. Б. Через точку В можно провести прямую, которая лежит в плоскости α. B. Любая прямая, которая проходит через точку В, не пересекает плоскость α. Г. Через точку В можно провести бесконечное множество плоскостей, которые пересекают плоскость α. 5. (1 б.) В пирамиде SA B C, все ребра которой равны, проведено сечение плоскостью, которая проходит через точки S, К, М, где точки К и М — середины ребер АС и А В. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Сечением является равнобедренный треугольник. Б. Сечением является правильный треугольник. B. Прямая SK принадлежит секущей плоскости и плоскости ASK. Г. Секущая плоскость пересекает прямую АВ в точке М. 6. (1 б.) В пространстве даны четыре точки А, В, С, D. Известно, что прямые АВ и СD — параллельны. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые АС и ВD лежат в одной плоскости. Б. Прямые АС и ВD могут быть скрещивающимися. B. Прямые АD и ВС обязательно параллельны. Г. Прямые АD и ВС лежат в одной плоскости. 7. (2 б.) В пространстве дана произвольная прямая а и точка А. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если через прямую а и точку А можно провести две разных плоскости, то точка А лежит на прямой а . Б. Если через прямую а и точку А можно провести только одну плоскость, то прямая а проходит через точку А. B. Через прямую а и точку А всегда можно провести плоскость. Г. Если плоскость проходит через прямую а , то она обязательно содержит точку А. 8. (2 б.) В пирамиде SAB C , все ребра которой равны, проведено сечение плоскостью, которая проходит через точки А, В, К, где К — середина ребра S C. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Сечением является правильный треугольник. Б. Сечением является прямоугольный треугольник. B. Длина отрезка АВ меньше длины отрезка В К. Г. Площадь сечения больше площади треугольника ABC. 9. (2 б.) В пространстве даны две скрещивающиеся прямые а и b и некоторая прямая с. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая с может пересекать прямую а и быть параллельной прямой b. Б. Прямая с может быть параллельной как прямой а, так и прямой b. B. Если прямые а и с лежат в одной плоскости, то прямые b и с обязательно скрещивающиеся. Г. Если прямые а и с лежат в одной плоскости, то прямые b и с не могут быть параллельными. 10. (3 б.) Прямые АВ, АС, АD не лежат в одной плоскости. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые ВС и АD могут пересекаться. Б. Точки А, В, С, D не лежат в одной плоскости. B. Можно провести четыре разные плоскости, каждая из которых содержит две прямые из данных прямых. Г. Можно провести четыре разные плоскости, каждая из которых г проходит через три точки из данных точек А, В, С, D. 11. (3 б.) В кубе ABCDA1B1C1D1 построено сечение плоскостью, которая проходит через точки D, A 1 , К, где точка К принадлежит ребру СС 1 причем СК = 2 КС 1 - Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Секущая плоскость и плоскости DСС 1 и А 1 В 1 С 1 имеют общую точку. Б. Сечением является трапеция, основания которой относятся как 3:1. B. Прямая DК пересекает плоскость D 1 С 1 В 1 в точке, которая принадлежит прямой В 1 С 1 . Г. Сечением является равнобокая трапеция. 12. (3 б.) Точки А, В, С, D не лежат в одной плоскости; точки К, L, М, N — середины отрезков АD, DС, ВС, АВ соответственно. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. ЕСЛИ КN = КL = LN, то LMN = 60°. Б. Прямая, проходящая через середины отрезков АС и ВD, может быть параллельна прямой КL. B. Длины отрезков КМ и NL обязательно равны. Г. Если АС = ВD = 2LN, то KLМ = 60°. Вариант 4 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) В пространстве дана прямая а и точка В вне её. Выберите правильное утверждение. A. Через прямую а и точку В можно провести две разные плоскости. Б. Через прямую а и точку В можно провести только одну плоскость. B. Через прямую а и точку В можно провести бесконечное множество плоскостей. Г. Через прямую а и точку В нельзя провести плоскость. 2. (0,5 б.) На рисунке изображен куб A BC D A 1 B 1 C 1 D 1 . Выберите правильное утверждение. A. Прямая A1D лежит в плоскости АDD1. Б. Прямая A1D не пересекает плоскость АBС. B. Прямая А1D является общей прямой плоскостей ABC и A1B1C1. Г. Плоскости АВВ1 и ABC пересекаются по прямой B1C. 3. (0,5 б.) Параллелограмм АВСВ и трапеция АВВ1С1 (АВ — основание трапеции) не лежат в одной плоскости. Выберите правильное утверждение. A. Прямые DС и С1D1 пересекаются. Б. Прямые DС и С1D1 лежат в одной плоскости. B. Прямые DС и С1D1 не параллельны. Г. Прямые DС и С1D1 скрещивающиеся. 4. (1 б.) В пространстве дана плоскость α и точка А, которая принадлежит плоскости α. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Любая прямая, которая проходит через точку А, обязательно пересекает плоскость α. Б. Любая прямая, которая проходит через точку А, обязательно лежит в плоскости α. B. Существуют прямые, которые проходят через точку А и не лежат в плоскости α. Г. Через точку А можно провести бесконечное множество плоскостей, отличных от плоскости α. 5. (1 б.) В пирамиде SAB C , все ребра которой равны, проведено сечение плоскостью, которая проходит через ребро АВ и точку К— середину ребра S C. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая ВК принадлежит секущей плоскости и плоскости S B C . Б. Сечением является правильный треугольник. B. Длина отрезка АК меньше длины отрезка АВ. Г. Сечением является равнобедренный треугольник, основание которого больше боковой стороны. 6. (1 б.) Даны две прямые а и b , через которые нельзя провести плоскость. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые а и b могут пересекаться. Б. Прямые а и b могут быть параллельными. B. Прямые а и b обязательно скрещивающиеся. Г. Через прямую а можно провести плоскость, которая пересекает прямую b. 7. (2 б.) В пространстве даны две разные плоскости α и β. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Плоскости α и β могут иметь только одну общую точку. Б. Если плоскости α и β проходят через разные точки А, В, С, то все эти точки лежат на одной прямой. B. Плоскости α и β могут иметь три общие точки, которые не лежат на одной прямой. Г. Если плоскости α и β имеют общую прямую а, то все общие точки этих плоскостей принадлежат а. 8. (2 б.) В пирамиде S ABC проведено сечение плоскостью, которая проходит через точки К, L, M — середины ребер SA, SB, SC. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Стороны треугольника KLM вдвое меньше сторон треугольника ABC. Б. Площадь треугольника KLM вдвое меньше площади треугольника ABC. B. Прямые МК и SB скрещивающиеся. Г. Секущая плоскость и плоскость SBC имеют общие точки. 9. (2 б.) В пространстве даны три различные прямые а, b, с. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если а и b скрещивающиеся и а и с скрещивающиеся, то b и с обязательно скрещивающиеся. Б. Если а и b пересекаются и а и с пересекаются, то b и с обязательно пересекаются. B. Если а и b параллельны и а и с параллельны, то прямые а , b, с обязательно лежат в одной плоскости. Г. Если а и b скрещивающиеся и а и с пересекаются, то прямые b и с могут лежать в одной плоскости. 10. (3 б.) В пространстве дана произвольная прямая а и две точки А, В вне этой прямой. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая а и точки А и В обязательно лежат в одной плоскости. Б. Если прямые а и АВ не пересекаются, то прямая а и точки А и В могут не лежать в одной плоскости. B. Если прямые а и АВ не пересекаются, то прямая а и точки А и В могут лежать в одной плоскости. Г. Обязательно существует плоскость, которая содержит прямую а и пересекает прямую АВ. 11. (3 б.) В кубе АВСDА1B1С1D1 построено сечение плоскостью, которая проходит через точки А, С, К, где точка К принадлежит ребру С1D1, причем КD1 = 2КС1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Секущая плоскость имеет с плоскостью А1ВС только одну общую точку С. Б. Секущая плоскость, плоскости АDD1и СDD1 проходят через одну точку. B. Сечением является равнобока трапеция, основания которой относятся как 1:2. Г. Секущая плоскость пересекает прямую DD1 в точке, которая принадлежит прямым СК и DD1. 12. (3 б.) Точки А, В, С, D не лежат в одной плоскости; точки K, L, М, N — середины отрезков АD, DС, ВС, АВ соответственно. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые КМ и DС могут пересекаться. Б. Прямые КМ и DС могут быть параллельными. B. Если АС = ВD, то угол NКМ обязательно равен углу КLМ. Г. Если АС = ВD то KL2 = КМ2 + LN2. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ Цель данного теста — проверить, умеет ли ученик: − определять взаимное расположение прямой и плоскости, используя соответствующие свойства и признаки; − определять взаимное расположение плоскостей в пространстве, используя соответствующие свойства и признаки; − применять свойства параллельного проектирования к изображению пространственных фигур на плоскости. Вариант 1 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) Дан куб A B C D А 1 B 1 C 1 D 1 . Выберите правильное утверждение. А. Прямая АВ пересекается с плоскостью DCC1. Б. Прямая АВ и плоскость B1C1D1 имеют общие точки. В. Прямая АВ параллельна плоскости, которая проходит через прямые DC и А1В1. Г. Прямая АВ параллельна плоскости В1С1С. 2. (0,5 б.) Дан прямоугольный параллелепипед ABCDA1BlC1D1. Выберите правильное утверждение. A. Плоскости ABC и A1B1C1 пересекаются. Б. Плоскости АВС и DCC1 не имеют общих точек. B. Плоскости ABВ1 и DCC1 параллельны. Г. Плоскости ADD1 и ВСС1 имеют общие точки. 3. (0,5 б.) Отрезок А1В1 — параллельная проекция отрезка АВ на плоскость α. Точка С лежит на отрезке АВ. Выберите правильное утверждение. A. Проекция точки С на плоскость α не принадлежит отрезку А 1 В 1 . Б. Отрезки АВ и А 1 В 1 не лежат в одной плоскости. B. Если АС : ВС = 2 : 3, то А 1 С 1 :С1В1= 2 : 3 Г. Если АС = СВ, то А 1 С 1 = 2 С 1 В 1 . 4. (1 б.) П а ра л л е л о гра м м A B C D и треугольник ABS лежат в разных плоскостях, MN — средняя л ини я т реу го л ьника A B S . Отметьте, какие из следующих четырех утверждений правильные, а какие —неправильные. A. Прямая MN пересекает плоскость ABC. Б. Прямая MN и плоскость ABC параллельны. B. Прямая BS параллельна плоскости ADC. Г. Прямая DC и плоскость ABS параллельны. 5. (1 б.) Точка О лежит между параллельными плоскостями α и β Две прямые а и b, которые проходят через точку О, пересекают плоскость α в точках А1, В1 а плоскость β — в точках А2, B2. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если А 1 B 1 = А 2 В 2 , то обязательно А 1 В 2 = В 1 А 2 . Б. Прямые А 1 В 1 и А 2 В 2 скрещивающиеся. B. Прямые А 1 В 1 и А 2 В 2 параллельны. Г. Прямые а и b лежат в одной плоскости. 6. (1 б.) Четырехугольник A 1 B 1 C 1 D 1 является параллельной проекцией трапеции AB CD ( AD — основание трапеции) на некоторую плоскость. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Четырехугольник A1B1C1D1 является трапецией с основанием A1B1. Б. Четырехугольник A1B1C1D1 может быть параллелограммом. B. Четырехугольник A1B1C1D1 является трапецией с основанием В1С1. Г. Четырехугольник A1B1C1D1 является трапецией с основанием А1D1. 7. (2 б.) Дан треугольник ABC. Плоскость α, параллельна прямой АВ, пересекает сторону АС в точке К, а сторону ВС — в точке L. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая KL пересекает прямую АВ. Б. Если АК = КС, то BL = LC. B. Треугольники ABC и KLC подобны. Г. Если CL = LB, KL = 12 см, то АВ > 24 см. 8. (2 б.) Даны две плоскости α и β, которые пересекаются. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Не существует прямой, которая параллельна как плоскости α, так и плоскости β. Б. Любая прямая, которая пересекает плоскость α, пересекает и плоскость β. B. Существует плоскость, которая параллельна как плоскости α, так и плоскости β. Г. Любая плоскость, которая пересекает плоскость α, пересекает также плоскость β. 9. (2 б.) Прямые a 1 и b 1 являются параллельными проекциями прямых а и b на некоторую плоскость. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если прямые а 1 и b1 параллельны, то обязательно прямые а и b тоже параллельны. Б. Если прямые а и b скрещивающиеся, то прямые a1 и b1 могут быть параллельными. B. Если прямые а 1 и b1 пересекаются, то прямые а и b обязательно пересекаются. Г. Если прямые а и b не пересекаются, то прямые а 1 и b1 обязательно не пересекаются. 10. (3 б.) Дан квадрат AB CD . Точка S равноудалена от каждой вершины квадрата, точки К, L, М — середины отрезков SA, SD, В С. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая КМ параллельна плоскости SCD. Б. Прямая LC пересекает плоскость SKM. B. Ч е т ы р е х у г о л ь н и к K L C M — параллелограмм. Г. Если SA = AD = 4 см, то КМ > π см. 11. (3 б.) Три параллельные плоскости α, β, γ пересекают скрещивающиеся прямые а и b в точках А1, А2, А3 и В1, В2, В3 (плоскость β лежит между плоскостями α и γ). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые А1В2 и А 2 В 3 могут быть параллельными. Б. Прямые В 1 А 2 и В 2 А 3 могут пересекаться. B. А 1 А 2 : А 2 А 3 = В 1 В 2 : В 2 В 3 . Г. А 1 А 3 :В 1 В 2 =А 1 А 2 :В 1 В 3 . 12. (3 б.) Прямоугольная трапеция А]В1С1D1 является изображением равнобокой трапеции АВСВ (АВ — основание трапеции), причем А1D1 = 4 см, А1B1 = 6 см, D1С1 = 9 см, M1 и N1 — середины сторон А1В1 и D1С1, В1F1 ┴ D1С1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. AB: D C = А 1 В 1 : С1D1. Б. Отрезок В1 F 1 является изображением высоты ВF трапеции А В СD. В. А 1 В 1 C 1 D 1 может быть изображением трапеции АВСD с основаниями АВ = 10 см и DС = 15 см и боковой стороной 4 см. Г. Отрезок М 1 N 1 является изображением высоты трапеции АВСD. Вариант 2 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) Дан куб A B C D A 1 B 1 C 1 D 1 . Выберите правильное утверждение. A. Прямая D 1 C 1 пересекает плоскость ABC. Б. Прямая D 1 C 1 имеет общие точки с плоскостью АВА 1 . B. Прямая D 1 C 1 параллельна плоскости A 1 B 1 B. Г. Прямая D 1 C 1 параллельна плоскости, которая проходит через прямые АА 1 и CC1. 2. (0,5 б.) Дан прямоугольный параллелепипед A B C D A 1 B 1 C 1 D 1 . Выберите правильное утверждение. А. Плоскости ABB1 и ВСС1 пересекаются. Б. Плоскости ABB1 и DCB не имеют общих точек. B. Плоскости ABB1и BCD параллельны. Г. Плоскости ADD1 и A1B1С1 параллельны. 3. (0,5 б.) Отрезок А 1 В 1 — параллельная проекция отрезка АВ на плоскость α. Точка С лежит на отрезке АВ. Выберите правильное утверждение. A. Прямые АА1 и ВВ1 не лежат в одной плоскости. Б. Проекция точки С на плоскость α лежит вне отрезка А1В1. В. Если АС = 3 см, АВ = 12 см, то АС : А1В1 = 1: 4. Г. Прямые АВ и A1B1 не лежат в одной плоскости. 4. (1 б.) Параллелограммы ABCD и ABKL лежат в разных плоскостях. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Плоскость ABC пересекается с прямой KL. Б. Плоскость ABC и прямая KL параллельны. B. Прямая АС параллельна плоскости BKL. Г. Прямая DC параллельна плоскости ABК. 5. (1 б.) Плоскости α и β параллельны. Параллельные прямые а и b пересекают плоскость α в точках А 1 , В 1 , а плоскость β — в точках А 2 , В 2 . Отметьте, какие из следующих четырех утверждений правильные, а какие – неправильные. A. Длина отрезка А1А2 равна длине отрезка В1В2. Б. Прямые А1В1 и А2В2 параллельны. B. Прямые А1В2 и А2В1 скрещивающиеся. Г. Прямые А1В2 и А2В1 пересекаются. 6. (1 б.) Четырехугольник А1В1С1D1 является параллельной проекцией квадрата АВСD на некоторую плоскость. Отметьте, какие из следующих четырех утверждений правильные, а какие – неправильные. A. В четырехугольнике А1В1С1D1 может не быть параллельных сторон. Б. В четырехугольнике А1В1С1D1 может не быть равных сторон. B. Четырехугольник А1В1С1D1 является трапецией. Г. Диагонали четырехугольника А1В1С1D1 точкой пересечения делятся пополам. 7. (2 б.) Дан треугольник АВС. Плоскость α пересекает сторону АС в точке К, а сторону ВС – в точке L, причем АВ║КL. Отметьте, какие из следующих четырех утверждений правильные, а какие – неправильные. A. Треугольник ABC не подобен треугольнику KLC. Б. Если АК = КС, то BL = LC. B. Прямая АВ параллельна плоскости α. Г. Если АВ = 24 см, АК : АС = 3 : 8, то KL = 12 см. 8. (2 б.) Даны две различные плоскости α и β. Отметьте, какие из следующих четырех утверждений правильные, а какие неправильные. A. Любая прямая, параллельная плоскости α, обязательно параллельна также плоскости β. Б. Любая плоскость обязательно пересекает хотя бы одну из плоскостей α или β. B. Если прямая а лежит в плоскости α, а прямая b в плоскости β, то прямые а и b обязательно параллельны. Г. Любая плоскость, параллельная плоскости α, обязательно параллельна также плоскости β. 9. (2 б.) Прямые а1 и b1 являются параллельными проекциями прямых а и b на некоторую плоскость. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если прямые а1 и b1 пересекаются, то прямые а и b могут быть скрещивающимися. Б. Если прямые а и b скрещивающиеся, то прямые а1 и b1 обязательно параллельны. B. Если прямые а и b лежат в одной плоскости, то прямые а1 и b1 могут пересекаться. Г. Если прямые а и b пересекаются, то прямые а1 и b1 пересекаются. 10. (3 б.) Дан квадрат АВСD. Точка S равноудалена от каждой вершины квадрата, точки К, L, М — середины отрезков SВ, SС, АD. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые КD и LM скрещивающиеся. Б. Прямая LD пересекает плоскость SАВ. π B. Если KL = 1 см, SD = 2 см, то DL < см. 2 Г. Четырехугольник KLDM может быть ромбом. 11. (3 б.) Три параллельные плоскости α, β, γ пересекают две данные скрещивающиеся прямые а и b в точках А 1 , А 2 , А3 и В1, В2, В3 соответственно (точка А 2 лежит между точками А 1 и А3, точка В2 лежит между точками В1 и В3). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые В1A3 и В2В3 пересекаются. Б. Если А2А3 = 2 см, В 1 В 2 = 8 см, А 1 А 2 = В2В3, то В 1 В 3 = 10 см. B. Прямые А1В1 и А3В3 могут быть параллельными. Г. А1А3 : В1В3=А2Аз : В2В3. 12. (3 б.) Параллелограмм А1В1С1D1 является изображением ромба АВСВ с углом А, который равняется 60°, причем А1F1 = F1D1, О1K1║B1F1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Отрезок B1F1 является изображением высоты ВF ромба АВСD. Б. Отрезок B1F1 является изображением биссектрисы угла АBС ромба АВСD. B. Отрезок О1K1 является изображением радиуса окружности, вписанной в ромб АВСD. Г. Отрезок О1F1 является изображением радиуса окружности, вписанной в ромб АВСD. Вариант 3 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) Дан прямоугольный параллелепипед ABCDA1B1C1D1. Выберите правильное утверждение. А. Прямая АА1 пересекает плоскость В1С1D1. Б. Прямая АА1 и плоскость ВСС1 имеют общие точки. В. Прямая АА1 параллельна плоскости, которая проходит через прямые А1D и В1С. Г. Прямая АА1 параллельна плоскости ВСD. 2. (0,5 б.) Дан куб ABCDA1B1C1D1. Выберите правильное утверждение. A. Плоскости CBB 1 и DAA 1 пересекаются. Б. Плоскости СВВ 1 и C 1 D 1 A 1 не имеют общих точек. B. Плоскости CDD 1 и ВАА 1 пересекаются. Г. Плоскости CDD 1 и ВАА 1 параллельны. 3. (0,5 б.) Треугольник А1В1С1 — параллельная проекция треугольника ABC на плоскость α. Выберите правильное утверждение. A. Если треугольник ABC равносторонний, то треугольник А1В1С1 обязательно равнобедренный. Б. Треугольник ABC обязательно равен треугольнику А1В1С1. B. Если ВК — высота треугольника ABC, то В1К1 обязательно высота треугольника А1В1С1 . Г. Если ВК — медиана треугольника ABC, то В1К1 обязательно медиана треугольника А1В1С1. 4. (1 б.) П а ра л л ел о г ра м м A B CD и трапеция AB K L ( А В — основание трапеции) лежат в разных плоскостях. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Плоскость АВК пересекает прямую DC. Б. Прямая KL параллельна плоскости ABC B. Прямая АС параллельна плоскости BKL Г. Прямая AL параллельна плоскости BCD. 5. (1 б.) Две параллельные плоскости α и β пересекаются плоскостью γ по прямым а и b. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые а и b могут быть скрещивающимися. Б. Прямые а и b обязательно параллельны. B. Прямая а параллельна плоскости β. Г. Любая прямая, которая лежит в плоскости γ, обязательно пересекает обе плоскости α и β. 6. (1 б.) Четырехугольник А1В1С1D1 является параллельной проекцией прямоугольника АВСD на некоторую плоскость. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Четырехугольник А1В1С1D1 является трапецией с основанием А1В1. Б. В четырехугольникеА1В1С1D1 нет равных сторон. B. В четырехугольнике А1В1С1D1 противоположные углы могут быть разными. Г. Диагонали четырехугольника А1В1С1D1 обязательно равны. 7. (2 б.) Плоскость α пересекает стороны ВА и ВС треугольника ABC в точках К и L, причем АК : ВК = CL : LB. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая АС параллельна плоскости α. Б. Если АК = ВК,АС = 10 см, то KL = 5 см. B. Прямая АС параллельна прямой KL. Г. Угол АСВ меньше угла KLB. 8. (2 б.) Даны две различные плоскости α и β . Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если две различные прямые, которые лежат в плоскости α, параллельны плоскости β, то α и β обязательно параллельны. Б. Если плоскости α и β параллельны некоторый прямой с, то α и β обязательно параллельны. B. Если плоскости α и β параллельны некоторой плоскости γ, то плоскости α и β обязательно параллельны. Г. Если две прямые плоскости α скрещиваются с двумя соответствующими прямыми плоскости β, то плоскости α и β обязательно параллельны. 9. (2 б.) Отрезки А1В1 и С1D1 являются параллельными проекциями отрезков АВ и СD. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если отрезки А1D1 и В1С1 пересекаются и точкой пересечения делятся пополам, то АВСD обязательно параллелограмм. Б. Если А1D1 = В1С1, то АВСD обязательно прямоугольник. B. Если АD = ВС, то А1В1С1D1 обязательно прямоугольник. Г. Если отрезки АD и ВС пересекаются и точкой пересечения делятся пополам, то А1В1С1D1 может быть параллелограммом. 10. (3 б.) Прямые а и b скрещивающиеся. На прямой а заданы точки А1, А2, А3, а на прямой b — точки В1, В2, В3. Точки М, N, К являются соответственно серединами отрезков А1B1, А2В2 и А3В3. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая а не пересекает плоскость МNК. Б. Прямая b обязательно параллельна плоскости МNК. B. Середина любого отрезка с концами на прямых а и b обязательно принадлежит плоскости МNК. Г. Если А 1 А 2 = 2 см, а В 1 В 2 = 3 см, то МN может равняться π см. 11. (3 б.) Прямые а и b, которые имеют общую точку, пересекают три данные параллельные плоскости α, β, γ в точках А1, А2, А3 и В1, В2, В3 соответственно (А2 лежит между А1 и Аз, В2 лежит между В1 и В3). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые А1В2 и А 2 В 3 скрещивающиеся. Б. Прямая а и точки В1 и В3 обязательно лежат в одной плоскости. B. Если А 1 А 2 = 25 см, В 2 В 3 = 4 см, А2А3 + В 1 В 2 = 20 см, то В1В3 = 14 см. Г. А1А3: А1А2 = В1В2: В1В3. 12. (3 б.) Точка О — точка пересечения диагоналей параллелограмма АВСD, α — плоскость, которая не пересекает параллелограмм. Через точки А, В, С, D, О проведены параллельные прямые, которые пересекают плоскость α соответственно в точках А1, В1, С1, D1, О1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если четырехугольник В1ВDD1 — параллелограмм, то четырехугольник А1АСС1 обязательно тоже параллелограмм. Б. АА1 + СС1 обязательно больше ВВ1. B. АА1 + СС1 + ВВ1 + DD1 – 4OO1 = 0. Г. Прямые АВ и D1С1 обязательно параллельны. Вариант 4 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) Дан прямоугольный параллелепипед ABCDA1B1C1D1. Выберите правильное утверждение. A. Прямая DC имеет общие точки с плоскостью BB1C1. Б. Прямая DC пересекает плоскость ABB1. B. Прямая DC параллельна плоскости, которая проходит через прямые AA1 и СС1. Г. Прямая DC параллельна плоскости ABC. 2. (0,5 б.) Дан куб ABCDA1B1C1D1. Выберите правильное утверждение. A. Плоскости ADD1 и ВСС1 пересекаются. Б. Плоскости ADD1 и A1B1C1 не имеют общих точек. B. Плоскости DСС1 и A1B1D1 параллельны. Г. Плоскости DCC1 и АВВ1 параллельны. 3. (0,5 б.) Четырехугольник А1В1С1D1 является параллельной проекцией трапеции АВСD (АВ — основание трапеции). Выберите правильное утверждение. A. Если АD = ВС, то обязательно А1D1 = В1C1. Б. Четырехугольник А1В1С1D1 обязательно трапеция. B. Прямые А1В1 и D1С1 могут пересекаться. Г. Если АВ = 2СD, то отрезки А1В1 и С1D1 могут быть равными. 4. (1 б.) Точка М лежит вне плоскости прямоугольника ABCD. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Плоскость ВСМ и прямая AD параллельны. Б. Плоскость ВСМ пересекает прямую AD. B. Плоскость АВМ параллельна прямой CD. Г. Прямая МА пересекает плоскость BCD. 5. (1 б.) Плоскости α и β параллельны. Скрещивающиеся прямые а и b пересекают плоскость α в точках А1, В1, а плоскость β — в точках А2, В2. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые А1В2 и В1А2 пересекаются. Б. Прямые А1B1 и А2В2 параллельны. B. Прямые А1В2 и А2В1 лежат в одной плоскости. Г. Через точки А1, А2, В1, В2 можно провести плоскость. 6. (1 б.) Четырехугольник А1В1С1D1 является параллельной проекцией ромба АВСD на некоторую плоскость. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Четырехугольник А1В1С1 D1 является трапецией с основанием В 1 С 1 . Б. В четырехугольнике А1В1С1 D1 диагонали точкой пересечения делятся пополам. B. В четырехугольнике А1В1С1 D1 противоположные стороны попарно равны. Г. Диагонали четырехугольника А1В1С1 D1 обязательно перпендикулярны. 7. (2 б.) Плоскость α пересекает стороны ВА и ВС треугольника ABC в точках К и L, причем АВ : КВ = ВС : BL. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая KL параллельна прямой АС. Б. Если АВ : КВ = 2, АС = 20 см, то KL = 10 см. B. Прямая АС параллельна плоскости α. Г. Угол ВАС больше угла BKL. 8. (2 б.) Даны две различные плоскости α и β. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если каждая прямая плоскости α не лежит в плоскости β, то плоскости α и β параллельны. Б. Если через точку М, которая не принадлежит плоскостям α и β, можно провести две разные прямые, параллельные плоскостям α и β, то плоскостям α и β обязательно пересекаются. B. Если любая плоскость γ, которая пересекает плоскость α, пересекает также плоскость β, то α и β обязательно параллельны. Г. Если любая плоскость пересекает плоскости α и β по параллельным прямым, то плоскости α и β может быть параллельны. 9. (2 б.) Отрезки А1В1 и С1D1 являются параллельными проекциями отрезков АВ и СD. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если прямая А1D1 параллельна В1С1, то прямая АС обязательно параллельна ВD. Б. Если прямые А1D1 и В1С1 пересекаются, то прямые АD и ВС обязательно пересекаются. B. Если прямые АD и ВС пересекаются, то прямые А1D1 и В1С1 обязательно пересекаются. Г. Если прямая АС параллельна прямой ВD, то прямая А1С1 обязательно параллельна В1D1. 10. (3 б.) Отрезки АВ и СD лежат на скрещивающихся прямых. Плоскость, которая параллельна прямым АВ и СD, пересекает отрезки АС, В С, ВD и АD соответственно в точках М, N, К , L. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. 1 1 А. Если АМ = ВN, то NС = МС. 2 2 Б. МN обязательно равняется LК. В. Прямая М L может пересекать плоскость В С D. Г. Если АВ = 2 см, СD = 3 см, то MN + NK может равняться π см. 11. (3 б.) Прямые а и b, которые пересекаются, пересекают три данные параллельные плоскости α, β, γ в точках А1, А2, А3 и В1, В2, В3 соответственно (плоскость β лежит между плоскостями α и γ). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямые А 1 В 1 и А3В3 скрещивающиеся. Б. Не существует прямой, которая бы пересекала прямые а и b и плоскости α, β, γ. B. Если А1А2 = 2 см, В2В3 = 8 см, А2А3 = В 1 В 2 , то В 1 В 3 = 12 см. Г. А1А2 : В1В2 = А1А3 : В1В3. 12. (3 б.) Точка О — точка пересечения медиан треугольника ABC, α — плоскость, которая не пересекает треугольник ABC. Через точки А, В, С, О проведены параллельные прямые, которые пересекают плоскость α соответственно в точках А1, В1, C1,О1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Четырехугольник A1ABB1 обязательно является параллелограммом. Б. Треугольник ABC обязательно подобен треугольнику А1В1С1. B. ЗОО1 = АА1 + СС1 + BB1. Г. Медианы треугольника A1B1C1 обязательно пересекаются в точке О1. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ Цель данного теста — проверить, умеет ли ученик: — — — использовать признак перпендикулярности прямой и плоскости для обоснования их взаимного расположения; применять свойства перпендикуляра и наклонных для сравнения их длин; находить расстояния от точки до плоскости, от прямой до параллельной ей плоскости, между параллельными плоскостями. Вариант 1 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) Точка S лежит вне плоскости ромба ABCD, причем SB ┴ ВС и SB ┴ АВ, BAD = 60°. Выберите правильное утверждение. A. Прямая SB перпендикулярна плоскости ABC. Б. Прямая АВ перпендикулярна прямой ВС. B. Прямая ВС перпендикулярна плоскости AS В. Г. Прямая SB не перпендикулярна прямой BD. 2. (0,5 б.) Из точки А к плоскости α проведен перпендикуляр А В и наклонные АС и А D . Выберите правильное утверждение. A. Прямая АВ не перпендикулярна прямой ВС. Б. Если АС > АD, то ВС > ВD. B. Если САВ = 45°, то АВ > ВС. Г. Среди отрезков АD, АВ, АС наибольшим является отрезок АВ. 3. (0,5 б.) ABCDA1B1C1D1 — прямоугольный параллелепипед, АВ = BB1 = 1 см, AD = 2 см. Выберите правильное утверждение. A. Расстояние от точки D до плоскости АВВ1 равно 1 см. Б. Расстояние от точки D до плоскости ВСС1 равно 2 см. B. Расстояние между прямой A1B1 и плоскостью ABC равно 1 см. Г. Расстояние между плоскостями ABB1 и DCC1 равно 1 см. 4. (1 б.) Дана плоскость α, перпендикулярная к ней прямая а и другая прямая b, которая не лежит в плоскости α. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если b || а, то b перпендикулярна α. Б. Если b ┴ α, то b | a. B. Если b ┴ α, то а и b скрещивающиеся. Г. Если b ┴ α, то а и b пересекаются. 5. (1 б.) Через центр О правильного треугольника ABC проведен перпендикуляр SO к плоскости ABC. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. SA = SB = SC. Б. Угол SAO равен углу SBO. B. Если AS = 5 см, ОА = 3 см, то SO = 3 см. Г. SB = SO. 6. (1 б.) Концы отрезка АВ расположены по одну сторону от плоскости α, точка С — середина отрезка АВ. Точки А и В находятся на расстоянии 13 см и 8 см от плоскости α, a расстояние между основаниями А 1 и В1 перпендикуляров, проведенных через точки А и В к плоскости α, равно 10 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Точка С находится на расстоянии 10 см от плоскости α. Б. Расстояние между прямыми AA 1 и ВВ1 больше 10 см. B. Расстояние от точки С до плоскости α равно сумме расстояний от точек А и В до плоскости α. Г. Длина отрезка АВ равна 13 см. 7. (2 б.) Расстояния от точки S до всех вершин квадрата ABCD одинаковые, точка О — центр квадрата. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая SO перпендикулярна плоскости АСВ. Б. Если SA =√2 см, АВ = √2 см, то SO = 1 см. B. Прямая BD перпендикулярна плоскости ACS. Г. Прямая BD перпендикулярна плоскости SCD. 8. ( 2 б.) Из точки А к плоскости α проведен перпендикуляр А В и наклонные АС и AD. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если АD = √6 см, АС = √3 см, АВ = √2 см, то BD - ВС = 1 см. Б. Если AD = √6 см, АС = √3 см, то BD > ВС. B. Если АС = 2 см, ACB = 60°, АD = 77 см, то BD = 2 см. Г. Если АD = АС, DAC = 60° и АВ = ВС, то DBC > 90°. 9. (2 б.) Точка К равноудаленна от вершин равнобедренного треугольника ABC, КО — перпендикуляр к плоскости ABC, расстояние от точки К до плоскости ABC равно 1 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Точка О обязательно является центром окружности, вписанной в треугольник ABC. Б. Точка О обязательно является центром окружности, описанной около треугольника ABC. B. Середина отрезка КА находится на расстоянии 1 см от плоскости ABC. Г. Если М, L, N — середины отрезков KA, КВ, КС, то расстояние между плоскостями ABC и MLN равно 0,5 см. 10. (3 б.) Дан прямоугольный параллелепипед ABCDA1B1C1D1, в котором АВ = а, ВС = b, СС1 = с (а < b < с). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Треугольник ABC 1 может быть тупоугольным. Б. Треугольник АВС 1 может быть равнобедренным. В. Отрезки АС 1 и BD 1 пересекаются в точке, которая является серединой каждого из них. Г. Величина угла C1AB равна arctg √𝑏 2 +𝑐 2 𝑎 . 11. (3 б.) В пирамиде SABC ребра SA, SB, SC попарно перпендикулярны и SA = SB = SC = а. Из точки S на плоскость ABC проведен перпендикуляр SO. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Точка О является точкой пересечения медиан треугольника ABC. Б. Длина перпендикуляра SO равна а √3 2 . B. Прямая SC перпендикулярна плоскости ABS. Г. Плоскость, которая проходит через ребро AS и перпендикулярна СВ, проходит через середину ребра СВ. 12. (3 б.) Через вершину В параллелограмма АВСD проведена плоскость на расстоянии 5 см от диагонали АС, точки К и М — середины отрезков АD и DС. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая АС параллельна проведенной плоскости. Б. Точка D находится на расстоянии 5 см от проведенной плоскости. B. Прямая КМ параллельна проведенной плоскости. Г. Расстояние от прямой КМ до построенной плоскости равно 5 см. Вариант 2 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) Точка S лежит вне плоскости треугольника ABC, причем SA┴AC и АВ┴АС, SA = АВ = SB . Выберите правильное утверждение. A. Прямая SA перпендикулярна плоскости ABC. Б. Прямая АВ перпендикулярна плоскости SAC. B. Прямая АС перпендикулярна плоскости SAB. Г. Прямая ВС перпендикулярна плоскости ASC. 2. (0,5 б.) Из точки А к плоскости α проведен перпендикуляр АВ и наклонные АС и АD. Выберите правильное утверждение. A. Прямая АD перпендикулярна плоскости α. Б. Прямая АD перпендикулярна прямой BD. B. Если АD = АС, то ВD < ВС. Г. Среди отрезков АС, АВ, АD наименьшим является АВ. 3. (0,5 б.) ABCDA1B1C1D1 — куб, ребро которого равно 1 см. Выберите правильное утверждение. A. Расстояние от точки А до плоскости ВСС1 меньше 1 см. Б. Расстояние от точки С до точки А равно 2 см. B. Расстояние от прямой A 1 B 1 до плоскости ABC равно 1 см. Г. Расстояние между плоскостями ABB1 и DCC 1 больше 1 см. 4. (1 б.) Дана плоскость α, параллельная ей прямая а и некоторая прямая b, которая не лежит в плоскости α. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если b || а, то b обязательно параллельна α. Б. Если b ┴ а, то b обязательно перпендикулярна α. B. Если b ┴ α и b пересекает а, то b ┴ а. Г. Если b ┴ α, то b и а обязательно скрещивающиеся. 5. (1 б.) Через центр О квадрата ABCD проведен перпендикуляр SO к плоскости ABC. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Расстояния SA, SB, SC, SD равны. Б. Угол SDO равен углу SAO. В. Если ОА = √2 см, SC = √3 см, то SO = 2 см Г. Если SA = 2ОА, то OSA = 45°. 6. (1 б.) Отрезок АВ, длина которого 13 см, не пересекает плоскость α, точка С — середина отрезка АВ. Расстояния от точек А и В до плоскости α равны 6 см и 1 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Расстояние от точки С до плоскости α равно 4 см. Б. Расстояние от точки С до плоскости α равно среднему арифметическому расстояний от точек А и В до плоскости α. B. Расстояние между перпендикулярами, проведенными из точек А и В к плоскости α, меньше 12 см. Г. Расстояние между перпендикулярами, проведенными из точек А и В к плоскости α, равно 12 см. 7. (2 б.) Расстояния от точки S до всех вершин прямоугольного треугольника ABC (C = 90°) одинаковые, точка О — середина гипотенузы АВ. Отметьте,. какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая СО обязательно перпендикулярна плоскости SAB. Б. Прямая СО обязательно перпендикулярна прямой SO. B. Прямая SO обязательно перпендикулярна плоскости ABC. Г. Если АС = 6 см, ВС = 8 см и CS = 13 см, то SO = 12 см. 8. (2 б.) Из точки А к плоскости α проведен перпендикуляр АВ и наклонные АС и AD. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если ВС = √3 см, BD = √2 см, то АС <AD. Б. Если АВ = √2 см, АС = √3 см, BD = √2 см, то ВС = 2 см, AD = 1 см. B. Если АС = 2 см, ACB = 45°, DB = √7 см, то AD = 4 см. Г. Если AD=AC и BC = DC, то DBC = 45°. 9. (2 б.) Точка К находится на расстоянии √𝟐 см от вершин равностороннего треугольника ABC со стороной √𝟑 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Основание перпендикуляра КО, проведенного к плоскости ABC, обязательно является центром вписанной в треугольник ABC окружности. Б. Расстояние от точки К до плоскости ABC равно 1 см. B. Середина отрезка КС находится на расстоянии 1 см от плоскости ABC. Г. Если M, L, N — середины отрезков KA, КВ, КС, то расстояние между плоскостями ABC и MLN равно 1 см. 10. (3 б.) Дан прямоугольный параллелепипед ABCDA1B1C1D1, в котором АВ = а, ВС = b , С С 1 = с ( а < b < с) . Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Треугольник АВС1 обязательно прямоугольный. Б. Треугольник АВС1 может быть правильным. B. Прямые АС1 и ВD1 перпендикулярны. Г. Величина угла АС1В равна arctg 𝑎 √𝑏 2 +𝑐 2 . 11. (3 б.) В пирамиде SA B C, каждое ребро которой равно а , из точки S проведен перпендикуляр SO к плоскости AB C. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Точка О — точка пересечения высот треугольника ABC. Б. Прямая АС перпендикулярна плоскости SOB. B. Проекция наклонной SA на плоскость ABC втрое меньше наклонной. Г. Угол между SB и SO равен arcсos √2 √3 . 12. (3 б.) Ребро куба ABCDA1B1C1D1 равно а . Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Расстояние от точки D до точки В 1 равно √5 а . Б. Расстояние от прямой ВС до прямой А 1 D 1 равно √3 а. 𝑎 B. Расстояние от вершины С до плоскости В D С 1 равно . √3 Г. Расстояние между плоскостью В D С 1 и прямой В 1 D 1 равно 𝑎 √2 . Вариант 3 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) Точка S лежит вне плоскости равнобокой трапеции АВСD (АВ || СD), SА┴АВ, SА┴АD. Выберите правильное утверждение. A. Прямые АD и АВ перпендикулярны. Б. Прямая АD перпендикулярна плоскости АВS. B. Прямая АS не перпендикулярна прямой АС. Г. Прямая АS перпендикулярна плоскости ВСD. 2. (0,5 б.) Из точки А к плоскости α проведен перпендикуляр АВ и наклонные АС и АD. Выберите правильное утверждение. A. Среди отрезков АD, АВ, DВ наименьшим является АD. Б. Среди отрезков АD, АВ, АС наименьшим является АВ. B. Если DВ > ВС, то АС > АD. Г. Если DВ = АВ, то DАВ = 30°. 3. (0,5 б.) ABCDA1B1C1D1 — прямоугольный параллелепипед, АD = 1 см, DС = 2 см, DD1 = 3 см. Выберите правильное утверждение. A. Расстояние от точки А до точки С равно 1 см. Б. Расстояние от точки D до плоскости BCC1 равно 2 см. B. Расстояние от прямой А 1 С 1 до плоскости ABC равно 2 см. Г. Расстояние между плоскостями АDD1 и ВСС1 равно 3 см. 4. (1 б.) В пространстве дана прямая а и точка А на ней. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Через точку А можно провести только одну прямую перпендикулярную прямой а. Б. Через точку А можно провести бесконечное множество прямых, перпендикулярных прямой а. B. Через точку А можно провести только одну плоскость, перпендикулярную прямой а. Г. Через точку А можно провести две различные плоскости, перпендикулярные прямой а. 5. (1 б.) Через центр О правильного шестиугольника ABCDEF проведен перпендикуляр SO к плоскости ABC. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Расстояния от точки S до вершин шестиугольника ABCDEF разные. Б. Угол OAS равен углу OCS. B. Если ОА = 1 см, SO = 1 см, то SA = √2 см. Г. Если SO = ОВ, то OSB = 30°. 6. (1 б.) Отрезок АВ не пересекает плоскость α, точка С — середина отрезка АВ. Расстояния от точек А и С до плоскости α соответственно равны 1 см и 3 см. Длина отрезка АВ равна 5 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Расстояние от точки В до плоскости α равно 5 см. Б. Расстояние от точки В до плоскости α может равняться 6 см. B. Расстояние между перпендикулярами AA1 и ВВ 1 проведенными к плоскости α, обязательно меньше 5 см. Г. Расстояние между параллельными плоскостями, которые проведены через перпендикуляры АА 1 и ВВ 1 к плоскости α, обязательно равно 3 см. 7. (2 б.) Расстояния от точки S до всех вершин прямоугольника ABCD одинаковые, точка О — точка пересечения диагоналей АС и BD прямоугольника ABCD. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая SO перпендикулярна прямой АС. Б. Прямая SO перпендикулярна плоскости ABC. B. Прямая АС обязательно перпендикулярна плоскости BDS. Г. Если АВ = 6 см, ВС = 8 см и AS = 13 см, то SO = 12 см. 8. (2 б.) Из точки А к плоскости α проведен перпендикуляр АВ и наклонные АС и AD. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Если АС - AD = 2 см, то ВС = BD. Б. Если АВ = √3 см, ВС = √6 см, AD = 2 см, то АС = 2 см, BD = 1 см. B. Если АВ = 2 см, BAD = 30°, СВ = √6 см, то АС = 4 см. Г. Если СВ = BD, AD = CD, то CAD = 45°. 9. (2 б.) Точка К равноудалена от вершин прямоугольного треугольника ABC (C = 90°), АС = 6 см, ВС = 8 см, КС = 13 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Основание перпендикуляра КО к плоскости ABC лежит на гипотенузе АВ. Б. Проекция отрезка КС на плоскость ABC равна 10 см. B. Расстояние от точки К до плоскости АВС равно 12 см. Г. Если М, L, N — середины отрезков KA, КВ, КС, то расстояние от точки К до плоскости MLN равно 5 см. 10. (3 б.) Ребро куба ABCDA1B1C1D1 , равно а. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Треугольник АВС1 равнобедренный. Б. Диагонали АС1, А1С, ВD1 и В1D куба пересекаются в точке, которая является серединой каждой из них. B. Расстояние от точки пересечения диагоналей куба до вершин куба равно √3 2 а. Г. Величина угла C1AB равна arctg√3. 11. (3 б.) Три отрезка SA, SB, SC попарно перпендикулярны, SA = SB = SC = а. Из точки S на плоскость ABC проведен перпендикуляр SO. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Точка О — точка пересечения биссектрис треугольника ABC. Б. Прямая АВ перпендикулярна плоскости SOC. а B. Длина перпендикуляра SO равна . √2 Г. Наклонные SA, SB, SC образуют с перпендикуляром SO углы, которые равны arcсos √3 3 . 12. (3 б.) Через большее основание AD трапеции ABCD проведена плоскость α, которая находится на расстоянии 10 см от меньшего основания ВС трапеции. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая ВС параллельна плоскости α. Б. Точка О — точка пересечения диагоналей АС и BD находится на расстоянии 5 см от плоскости α. B. Средняя линия M N трапеции ABCD находится на расстоянии 6 см от плоскости α. Г. Если AD = 18 см, ВС = 12 см, то точка О — точка пересечения диагоналей АС и BD трапеции ABCD — находится на расстоянии 6 см от плоскости α. Вариант 4 Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите А Б В Г.Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным. 1. (0,5 б.) Точка S лежит вне плоскости треугольника ABC, SA ┴АС, SA┴AB, АС = АВ, BAC = 40°. Выберите правильное утверждение. A. Прямые АВ и ВС перпендикулярны. Б. Прямая SA перпендикулярна плоскости АВС. B. Прямая АВ перпендикулярна плоскости SAC. Г. Прямая АС перпендикулярна плоскости SAB. 2. (0,5 б.) Из точки А к плоскости α проведен перпендикуляр АВ и наклонные АС и AD. Выберите правильное утверждение. A. Прямая АС перпендикулярна плоскости α. Б. Прямая АС перпендикулярна прямой ВС. B. Среди отрезков АС, АВ, ВС наибольшим является ВС. Г. Среди отрезков АС, АВ, ВС наибольшим является АС. 3. (0,5 б.) ABCDA1B1C1D1 — прямоугольный параллелепипед, AD = 2 см, DC = СС1 = 1 см. Выберите правильное утверждение. A. Расстояние от точки А до плоскости BCC1 равно 2 см. Б. Расстояние от точки А до точки С равно 2 см. B. Расстояние от прямой В1А1 до плоскости ABC равно 1 см. Г. Расстояние между плоскостями АВВ1 и DCC1 равно 1 см. 4. (1 б.) В пространстве дана прямая а и точка А вне её. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Через точку А можно провести две различные плоскости, которые перпендикулярны прямой а. Б. Через точку А можно провести только одну плоскость, перпендикулярную прямой а. B. Через точку А можно провести только одну прямую, которая перпендикулярна прямой а и пересекает ее. Г. Через точку А можно провести две прямые, которые пересекают прямую а и перпендикулярны ей. 5. (1 б.) Через точку О пересечения диагоналей АС и BD прямоугольника ABCD проведен перпендикуляр SO к плоскости ABC. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Расстояния от точки S до вершин прямоугольника разные. Б. Угол OSC больше угла OSB. B. Если ОА = √2 см, SO = √2 см, то SA = 2√2 см. Г. Если SA = 10 см, ОА = 5 см, то SAO = 30°. 6. (1 б.) Отрезок АВ расположен по одну сторону от плоскости α, точка С — середина отрезка А В. Расстояния от точек В и С до плоскости α соответственно равны 3 см и 5 см, а расстояние между перпендикулярами, проведенными через точки А и В к плоскости α, равно 3 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Расстояние от точки А до плоскости α равно 8 см. Б. Расстояние от точки А до плоскости α больше, чем расстояние от точки В до плоскости α. B. Длина отрезка АВ равна 5 см. Г. Расстояние между параллельными плоскостями, которые проведены через перпендикуляры AA 1 и BB 1 к плоскости α, больше 3 см. 7. (2 б.) Расстояния от точки S до всех вершин прямоугольного треугольника ABC ( C = 90°) одинаковые, АС = ВС, точка О — середина гипотенузы АВ . Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая SO перпендикулярна прямой АВ. Б. Прямая SO перпендикулярна плоскости ABC. B. Прямая СО перпендикулярна плоскости ASB. Г. Если АС = √2 см, AS = √2 см, то SO = 2 см. 8. (2 б.) Из точки А к плоскости а проведен перпендикуляр А В и наклонные А С и A D. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Если BD - BC = 1 см, то AD = АС. Б. Если АВ = √2 см, ВС = √7 см, BD = √2 см, то АС = 3 см, AD = 2 см. В. Если AD = 2 см, BAD = 45°, АС = √3 см, то СВ = 1 см. Г. Если АС = AD, DAC = 60° и АВ = BD, то DBC = 60°. 9. (2 б.) Точка К находится на расстоянии √𝟐 см от каждой вершины квадрата A BC D, диагональ которого равна 2 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Точка О — основание перпендикуляра КО к плоскости ABC — является центром вписанной в квадрат ABCD окружности. Б. Расстояние между прямыми АВ и CD равно √2 см. B. Расстояние от точки К до плоскости квадрата ABCD равно 1 см. Г. Если M , L , N — середины отрезков KA, КВ, КС, то расстояние между плоскостями ABC и MLN равно 1 см. 10. (3 б.) Ребро куба ABCDA1B1C1D1 равно а. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Треугольник АВС1 тупоугольный. Б. Центр окружности, описанной около треугольника АВС1, лежит на АС1. B. Диагонали куба АС1 и DB1 перпендикулярны. Г. Величина угла ВС1А равна arctg √2 2 . 11. (3 б.) Три отрезка SA, S B и S C имеют одинаковую длину а . AS B = B S C = C SA = 60°. Из точки S проведен перпендикуляр SO к плоскости AB C. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Прямая SA перпендикулярна плоскости SBC. а Б. Длина перпендикуляра SO равна . √6 B. Плоскость, которая проходит через прямую АС и перпендикулярна прямой SB, делит отрезок SB пополам. Г. Угол между наклонной SA и перпендикуляром SO равен arcсos √3 √2 . 12. (3 б.) В прямоугольном параллелепипеде AB CD A 1 B l C 1 D l A B 1 = √𝟓 см, А С 1 = √𝟔 см, АВ = 2 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. A. Расстояние между плоскостями ABC и A1B1C1 равно √2 см. Б. Расстояние между прямыми АВ и CD равно 1 см. B. Расстояние между прямыми AB1 и DC1 равно √2 см. Г. Расстояние между прямой A1D1 и плоскостью АВ1С1 равно 2 √5 см. Ответы к тестам