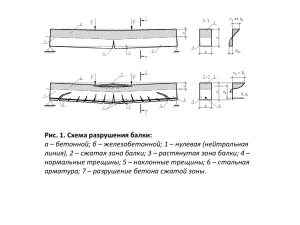
1.Перечислить расчеты по предельным состояниям второй группы. Ограничения, связанные с предельными состояниями второй группы. Расчетные условия в общем виде. Предельные состояния второй группы затрудняют нормальную эксплуатацию конструкций и связаны с ограничением: а) чрезмерных деформаций и перемещений, неблагоприятно воздействующих на внешний вид конструкции, затрудняющих протекание технологических процессов, создающих повреждения отделки и других неконструктивных (декоративных и вспомогательных) элементов; б) недопустимого трещинообразования в бетоне конструкции, неблагоприятно влияющего на ее внешний вид и долговечность; в) вибрационных воздействий, создающих дискомфорт для людей, повреждения зданий или их частей. Расчеты по предельным состояниям второй группы: - расчеты по тещиностойкости: а) расчеты по образованию трещин; б) расчеты по раскрытию трещин; в) расчеты по закрытию (зажатию) трещин (должны выполнятся условия декомпрессии). - расчеты по деформациям: прогибы и перемещения. При расчете по предельным состояниям второй группы проверяется общее условие, согласно которому значения расчетных эффектов, вызванных воздействиями Ск (например, ширина раскрытия трещин или прогибы) не должны превышать допустимых значений, установленных нормативным документом: Ск [Сlim ] где Ск - расчетное значение прогиба или ширины раскрытия трещин, Сlim - допустимое значение прогиба или ширины раскрытия трещин установленное нормативным документом с точки зрения обеспечения нормальных условий эксплуатации конструкции. 2. Натяжение арматуры на упоры Контролируемое напряжение и удлинение. механическим способом. Как правило, механическое натяжение арматуры осуществляется гидравлическими и винтовыми домкратами. Можно использовать и простейшие грузовые устройства и приспособления, представляющие собой систему лебедок, блоков, рычагов и полиспастов, оснащенных динамометрами. Раскладку прядей арматуры производят по принципу полиспаста. Арматуру натягивают на упоры стенда или формы. При этом натяжение может осуществляться одиночными стержнями, группами стержней или одновременно всей арматурой. Во всех случаях необходимо соблюдать условия симметричности и равномерности передачи усилий от напрягаемой арматуры на днище формы. Кроме того, необходима и определенная последовательность передачи механических усилий на арматуру. Первоначально передается усилие, составляющее 45-50 % от проектного значения. При таком натяжении проверяется правильность расположения стержней и анкерных устройств. Затем натяжение арматуры доводят до усилия, превышающего проектное на 10 %, делается выдержка напряжения в течение 3-5 мин, после чего усилия в арматуре снижают до проектных. Процесс механического натяжения арматуры заключается в укладке полного комплекта подготовленных мерных стержней в упоры подвижной и неподвижной траверс силовой формы - установки. К подвижной траверсе крепятся гидравлические домкраты, каждый из которых одним концом упирается в форму - установку, а другим перемещает подвижную траверсу. Натяжение арматуры контролируется электроконтактным манометром. По достижении заданного усилия натяжения подвижная траверса фиксируется. После передачи натяжения на бетон фиксаторы убираются. Траверса может одновременно натягивать до 30 стержней. Предварительное напряжение σ0,mах следует назначать с учетом допустимых отклонений значения предварительного напряжения ρ таким образом, чтобы выполнялись условия: где kр = 0,9 — для стержневой арматуры; kр = 0,8 — для проволочной арматуры». Значение р при механическом способе натяжения арматуры следует принимать равным 0,050,max, а при электротермическом и электротермомеханическом способах определять по формуле и p 30 360 , l где l — длина натягиваемого стержня (расстояние между наружными гранями упоров), м; р — в МПа. Контролируемое удлинение стержня Ep –модуль упругости напрягаемой арматуры 3. Потери предварительного напряжения, виды потерь. Технологические потери (первые потери в момент времени t = t0) 1) Потери от релаксации напряжений арматуры следует определять по формулам: а) при механическом способе натяжения: — проволочной Pir 0,22 0,max 0,1 0,max Ap ; fpk (9.6) Pir 0,1 0,max 20 Ap ; (9.7) — стержневой б) при электротермическом и электротермомеханическом способах натяжения: — проволочной Pir 0,05 0,max Ap ; (9.8) — стержневой Pir 0,03 0,max Ap . (9.9) Если потери предварительного напряжения, определенные по формулам (9.6), (9.7), окажутся отрицательными, их следует принимать равными нулю. 2) Потери от температурного перепада, определяемого как разность температур натянутой арматуры в зоне нагрева и устройства, воспринимающего усилие натяжения при прогреве бетона, следует рассчитывать по формулам: — для бетонов классов от С12/15 до С30/37 PT 1,25T Ap ; (9.10) — для бетонов классов С35/45 и выше PT 1,0T Ap где , (9.11) Т — разность между температурой нагреваемой арматуры и неподвижных упоров (вне зоны прогрева), воспринимающих усилие натяжения, С. При отсутствии точных данных допускается принимать Т = 65 С. В формулах (9.10) и (9.11) Ap — в мм2; PT — в H. При подтягивании напрягаемой арматуры в процессе термообработки на величину, компенсирующую потери от температурного перепада, последние принимают равными нулю. 3) Потери от деформации анкеров, расположенных в зоне натяжных устройств, при натяжении на упоры следует рассчитывать по формуле, мм PA где l l Es Ap , l (9.12) — длина натягиваемого стержня (расстояние между наружными гранями упоров стенда или формы), мм; l — обжатие опрессованных шайб, смятие высаженных головок и т. п., принимаемое равным 2 мм; смещение стержней в инвентарных зажимах, определяемое по формуле, мм l = 1,25 + 0,15 , здесь — диаметр, натягиваемого стержня, мм. 91 4) Потери, вызванные проскальзыванием напрягаемой арматуры в анкерных устройствах, происходящие на длине зоны проскальзывания х0 (рисунок 9.1), при натяжении арматуры на бетон следует определять по формуле Psl 2ap x0 x Es Ap , x02 (9.13) где ар — величина проскальзывания, определяемая опытным путем для соответствующего типа анкерного устройства; для анкеров стаканного типа, колодок с пробками следует принимать ар 5 мм; х —длина участка от натяжного устройства до расчетного сечения; в случае, если х х0 следует принимать Psl 0 . 5) Потери, вызванные деформациями стальной формы, при закреплении на ее упорах напрягаемой арматуры следует определять по формуле Pf где — l Es Ap , l (9.16) коэффициент, определяемый по формулам: при натяжении арматуры домкратом n 1 ; 2n при натяжении арматуры электромеханическим (50 % усилия создается грузом) намоточной машиной способом n 1 , 4n здесь n — число групп стержней, натягиваемых неодновременно; l — сближение упоров по линии действия усилия Р0, определяемое из расчета деформации формы; l — расстояние между наружными гранями упоров. При отсутствии данных о технологии изготовления изделий и конструкции формы потери усилия предварительного напряжения от ее деформаций принимают равными 30Ap, в Н, где Ap — в мм2. При электротермическом способе натяжения потери от деформации формы в расчете не учитываются, т. к. они учтены при определении полного удлинения арматуры. 6) Потери, вызванные трением арматуры о стенки каналов или о поверхность бетона конструкции, для напрягаемой арматуры как с прямолинейной так и с криволинейной трассой потери при натяжении на бетон следует определять по формуле P x P0 1 exp x , м; (9.17) где , — коэффициенты, определяемые по таблице 9.4; х — длина участка от натяжного устройства до расчетного сечения, — суммарный угол поворота трассы (оси) напрягаемой арматуры, рад (рисунок 9.1); Р0 — усилие обжатия без учета потерь, передаваемое натяжным устройством. 9.3.1.7 Потери, вызванные трением напрягаемой арматуры об огибающие приспособления, при ее натяжении на упоры, следует определять по формуле P x P0 1 exp( ) , (9.18) где — коэффициент, принимаемый равным 0,25. 8) Потери, вызванные упругой деформацией бетона, следует определять для элементов с натяжением напрягаемой арматуры на упоры. В элементах с натяжением арматуры на бетон этот вид потерь следует учитывать только в случае последовательного отпуска напрягаемых стержней. Значения потерь следует определять по формулам: — при натяжении на упоры A 2 Pc p 1 zcp c P0,c ; Ic (9.19) — при натяжении на бетон Pc где p = Ap Ac Es Ecm A n 1 2 p 1 zcp c 2n Ic P0,c , (9.20) ; ; n — количество напрягаемых стержней; Р0,с — усилие предварительного напряжения с учетом потерь, реализованных к моменту обжатия бетона. Усилие предварительного обжатия Рт,0 к моменту времени t = t0, действующее непосредственно после передачи усилия предварительного обжатия на конструкцию (при натяжении на упоры) или после завершения натяжения (при натяжении на бетон), должно быть не более Pm,0 pm,0 Ap 0,75fpk Ap . (9.21) В формуле (9.21) величину Рт,0 определяют — для элементов с натяжением на упоры Pm,0 P0 Pc Pir P ( x ) PТ PA Pf — для элементов с натяжением на бетон ; (9.22) Pm,0 P0 Pc Pir P ( x ) Psl . (9.23) 2 Эксплуатационные потери (вторые потери в момент времени t > t0) 2.1 При расчете среднего значения усилия предварительного обжатия Pm,t к моменту времени эксплуатации конструкции t > t0 дополнительно к первым технологическим потерям, определенным по 9.3.1, следует учитывать потери от усадки и ползучести бетона, долговременной релаксации напрягаемой арматуры, а также потери от смятия бетона под витками спиральной или кольцевой арматуры и обжатия стыков между отдельными блоками для конструкций, в которых натяжение арматуры осуществляется на бетон. 2.2 Реологические потери, вызванные ползучестью и усадкой бетона, а также длительной релаксацией напряжений в арматуре следует определять по формуле Pt t p,c s r Ap , (9.24) где p,c+s+r — потери предварительного напряжения, вызванные ползучестью, усадкой и релаксацией напряжений на расстоянии х от анкерного устройства в момент времени t p,c s r cs (t, t0 ) E p pr p (t, t0 ) cp cp,0 1 p Ap A 2 1 c zcp 1 0,8 (t, t0 ) Ac Ic ; (9.25) сs(t,t0) — ожидаемое значение усадки бетона к моменту времени t, определяемое по приложению Б либо принимаемое в соответствии с указаниями подраздела 6.1; (t,t0) — коэффициент ползучести бетона за период времени от t0 до t, определяемый по приложению Б либо принимаемый в соответствии с указаниями подраздела 6.1; cp — напряжения в бетоне на уровне центра тяжести напрягаемой арматуры от практически постоянного сочетания нагрузок, включая только собственный вес; cp,0 — начальное напряжение в бетоне на уровне центра тяжести напрягаемой арматуры от действия усилия предварительного обжатия (с учетом первых потерь в момент времени t = t0); pr — изменения напряжений в напрягаемой арматуре в расчетном сечении, вызванные релаксацией арматурной стали. Допускается определять по таблицам 9.2 и 9.3 в зависимости от уровня напряжений σ0,max/fpk, принимая σ0,max = σpg,0; σpg,0 — напряжения в арматуре, вызванные натяжением (с учетом первых потерь в момент времени t = t0) и действием практически постоянного сочетания нагрузок. При этом суммарная величина изменения напряжений в напрягаемой арматуре в расчетном сечении от релаксации арматурной стали и от потерь σpr,0 = Pir/Ap, где Pir определяемая по формуле (9.6), не должна превышать максимальные потери начальных напряжений в арматуре по таблице 9.2 при σ0,max/fpk = 0,8; p = Ep /Ecm, Ер — модуль упругости напрягаемой арматуры; Ac, Ic zcр арматуры. — соответственно площадь и момент инерции сечения; — расстояние между центрами тяжести сечения и напрягаемой В формуле (9.25) сжимающие напряжения и соответствующие относительные деформации следует принимать со знаком «плюс». 2.3 Потери от смятия бетона под витками спиральной или кольцевой арматуры, натягиваемой на бетон, при диаметре конструкции до 3 м следует определять по формуле Psp 70 0,22Dext Ap , (9.26) где Dext — наружный диаметр конструкции, см. 2.4 Потери, вызванные деформациями обжатия стыков между блоками для конструкций, состоящих из отдельных блоков, следует определять по формуле Pob n l Ep Ap , l (9.27) где n — число швов конструкции и оснастки по длине натягиваемой арматуры; l — обжатие стыков, принимаемое равным, мм: 0,3 — для стыков, заполненных бетоном; 0,5 — при стыковании насухо; l — длина натягиваемой арматуры, мм. 4. Стадии Н.Д.С. при эксплуатации железобетонных конструкций. Привести графики распределения напряжений в арматуре и бетоне для стадий Н.Д.С. (на примере изгибаемого элемента). 5. Понятие трещиностойкости железобетонных конструкций. Условия, влияющие на скорость и степень коррозионных процессов. Трещиностойкость - способность железобетонной конструкции сопротивляться образованию и раскрытию трещин. Трещиноватость бетона, или способность к образованию трещин, является характерным его свойством, отличающим его от целого ряда строительных материалов. Трещины в бетоне конструкций образуются уже в процессе формирования структуры в результате развития физико-химических процессов, происходящих при твердении цемента. Это так называемые микротрещины, возникающие в результате усадочных и температурных явлений, сопровождающих реакции гидратации портландцементного вяжущего. Такие трещины располагаются хаотично как внутри структуры бетона, так и на поверхности изделия (контракционные трещины). Микротрещины, являющиеся результатом химической усадки и температурных эффектов при твердении оказывают отрицательное влияние на эксплуатационные свойства бетона, приводят к снижению его долговечности. Вместе с тем, такие трещины практически не поддаются расчету, а ограничиваются исключительно технологическими мероприятиями на стадии проектирования составов бетонной смеси и выбора рациональных методов ее укладки в конструкцию. Расчет по образованию трещин: - по образованию нормальных трещин N sd Ncr - центральное растяжение M sd M cr - изгиб, внецентренное сжатие и растяжение M sd , N sd - момент относительно выбранное оси, проходящей в сечении, и продольное растягивающее усилие, определенное от соответствующего сочетания нагрузок; M cr , Ncr - соответственно момент и усилие, воспринимаемое сечением, нормальным к продольной оси элемента при образовании трещин. Ncr fctm Ac без предварительного напряжения M cr fctm W Ncr f ctm A0 P0 с предварительным напряжением M cr f ctm W P0 l0 Расчет по раскрытию трещин: wk wlim Расчет по раскрытию нормальных трещин wk srm rm где srm - среднее расстояние между трещинами, rm - средние относительные деформации арматуры, определяемые при соответствующем сочетании нагрузок, - коэффициент, учитывающий отношение расчетной расчетной ширины раскрытия трещин к средней. 1.7 - при расчете ширины раскрытия трещин, образующихся от усилий, вызванных соответствующим сочетанием нагрузок, а также от усилий, возникающих при ограничении вынужденных деформаций для сечений, наименьший размер которых (высота, ширина, толщина) превышает 800 мм; 1.3 - при расчете ширины раскрытия трещин, образующихся от действий усилий, возникающих при ограничении вынужденных деформаций для сечений, наименьший размер которых (высота, ширина, толщина) составляет 300 мм и менее. 6. Расчеты по 2-ой группе предельных состояний. Расчетные условия. Расчёт по раскрытию трещин в общем виде согласно п.8.2.1.1 [1] следует производить из условия: wk wlim ; где: wk – расчётная ширина раскрытия трещин; wlim – предельная допустимая ширина раскрытия трещин, определяемая по таблице 5.1 [1]. Таблица 5.1 Предельно допустимые значения ширины раскрытия трещин wlim , в миллиметрах Железобетонные элементы Предварительно напряженные Класс по элементы условиям эксплуатации по Практически постоянное Частое сочетание таблице 5.2 сочетание нагрузок по нагрузок по приложению А приложению А Х0, ХС1 0,4 0,2 ХС2, ХС3, ХС4 0,3 0,2* ХА1, ХА2,ХD1, ХD2 По СНиП 2.03.11 Не допускается wk = srmsm , (8.6) где srm — среднее расстояние между трещинами; sm — средние относительные деформации арматуры, определяемые при соответствующем сочетании нагрузок; — коэффициент, учитывающий отношение расчетной ширины раскрытия трещин к средней. Среднее расстояние srm между трещинами, мм, нормальными к продольной оси, в изгибаемых и растянутых элементах следует определять по формуле srm 50 0,25k1 k2 eff 2 Расчет по раскрытию наклонных трещин Расчетную ширину wk наклонных трещин следует определять по формуле (8.6) с заменой среднего расстояния между трещинами srm на sr,max, рассчитываемого по формуле (8.11). Для элементов, имеющих ортогональное армирование, в случае, когда образующиеся трещины наклонены под углом к продольной оси элемента (направлению продольного армирования), и угол наклона > 15, среднее расстояние между наклонными трещинами sr,max следует определять по формуле sr ,max 1 sin cos , sr ,max,x sr ,max,y (8.11) где sr,max,x — средний шаг трещин в направлении, параллельном продольной оси элемента; sr,max,y — средний шаг трещин в направлении, перпендикулярном к продольной оси элемента; — угол между направлением продольного армирования (продольной осью элемента) и направлением главных сжимающих напряжений. Значение принимается согласно 7.2.2.26. 3) Расчет железобетонных конструкций по деформациям следует производить из условия ak alim , где ak — прогиб (перемещение) железобетонной конструкции от действия внешней нагрузки, мм; alim — предельно допустимый прогиб (перемещение), мм, принимаемый по разделу 10 СНиП 2.01.07. 7. Расчеты по 2-ой группе предельных состояний. Допустимая ширина раскрытия трещин, прогибы. Предельно допустимые значения ширины раскрытия трещин Класс по условиям эксплуатации Х0, ХС1 ХС2, ХС3, ХС4 XA1,XA2,XD1,XD2 Железобетонные элементы Практически постоянное сочетание нагрузок 0,4 Предварительно напряженные элементы Частое сочетание нагрузок 0,2 0,2* Не допускается 0,3 По ТКП 45-2.01111-2008 * Для этих классов по условиям эксплуатации при действии практически постоянного сочетания нагрузок должно выполняться условие декомпрессии (отсутствие растягивающих напряжений в бетоне на уровне напрягаемой арматуры).» Элементы конструкций Предъявляемые требования Балки, фермы, ригели, прогоны, плиты, настилы (включая поперечные ребра плит и настилов): Эстетикоа) покрытий и психологические перекрытий, открытых для обзора, при пролете l, м: l1 l=3 l=6 l = 24 (12) l 36 (24) Вертикальные предельные прогибы fu Нагрузки для определения вертикальных прогибов Постоянные и временные длительные l/120 l/150 l/200 l/250 l/300 Предельные прогибы Расчет железобетонных конструкций по деформациям следует производить из условия ak alim , где ak — прогиб (перемещение) железобетонной конструкции от действия внешней нагрузки, мм; alim — предельно допустимый прогиб (перемещение), мм, принимаемый по разделу 10 СНиП 2.01.07. Расчёт по раскрытию трещин в общем виде согласно п.8.2.1.1 [1] следует производить из условия: wk wlim ; где: wk – расчётная ширина раскрытия трещин; wlim – предельная допустимая ширина раскрытия трещин, определяемая по таблице wk = srmsm , (8.6) где srm — среднее расстояние между трещинами; sm — средние относительные деформации арматуры, определяемые при соответствующем сочетании нагрузок; — коэффициент, учитывающий отношение расчетной ширины раскрытия трещин к средней. 8. Расчет ширины раскрытия наклонных трещин по. Понятие Sr,max. Расчёт по раскрытию трещин в общем виде согласно п.8.2.1.1 [1] следует производить из условия: wk wlim ; где: wk – расчётная ширина раскрытия трещин; wlim – предельная допустимая ширина раскрытия трещин, определяемая по таблице wk = srmsm , (8.6) где srm — среднее расстояние между трещинами; sm — средние относительные деформации арматуры, определяемые при соответствующем сочетании нагрузок; — коэффициент, учитывающий отношение расчетной ширины раскрытия трещин к средней. Среднее расстояние srm между трещинами, мм, нормальными к продольной оси, в изгибаемых и растянутых элементах следует определять по формуле srm 50 0,25k1 k2 eff Расчетную ширину wk наклонных трещин следует определять по формуле (8.6) с заменой среднего расстояния между трещинами srm на sr,max, рассчитываемого по формуле (8.11). Для элементов, имеющих ортогональное армирование, в случае, когда образующиеся трещины наклонены под углом к продольной оси элемента (направлению продольного армирования), и угол наклона > 15, среднее расстояние между наклонными трещинами sr,max следует определять по формуле sr ,max 1 sin cos , (8.11) sr ,max,x sr ,max,y где sr,max,x — средний шаг трещин в направлении, параллельном продольной оси элемента; sr,max,y — средний шаг трещин в направлении, перпендикулярном к продольной оси элемента; — угол между направлением продольного армирования (продольной осью элемента) и направлением главных сжимающих напряжений. Значение принимается согласно 7.2.2.26. 9. Упрощенная методика определения wk по условию max для прямоугольных элементов Ж.Б.К. без преднапряжения. Последовательность расчета. ф-ла 10.16 : wk = srmsm , где srm — среднее расстояние между трещинами; sm — средние относительные деформации арматуры, определяемые при соответствующем сочетании нагрузок; — коэффициент, учитывающий отношение расчетной ширины раскрытия трещин к средней. Среднее расстояние srm между трещинами, мм, нормальными к продольной оси, в изгибаемых и растянутых элементах следует определять по формуле srm 50 0,25k1 k2 eff 10.Расчетные модели для определения прогибов 11. Упрощенный способ определения сс и s по СНБ 5.03.01–02 при определении кривизны с трещинами. Кривизну железобетонных элементов (или участков элементов) с трещинами 1 , нормальными к продольной оси, следует определять по r cr формуле cm sm,0 1 r , d cr (8.19) где cm — средние относительные деформации крайнего сжатого волокна бетона на участке между трещинами; sm,0 — средние относительные деформации крайнего растянутого стержня продольной арматуры на участке между трещинами; d — расстояние между крайним сжатым волокном бетона и крайним растянутым стержнем продольной арматуры. Значение cm определяют по формуле cm c cc , (8.20) где cс — относительная деформация крайнего сжатого волокна бетона в сечении с трещиной; с — коэффициент, учитывающий неравномерность распределения относительных деформаций сжатого бетона между трещинами. Значение коэффициента допускается принимать равным 0,9. Значение sm определяют в соответствии с указаниями 5.5.3.2 и 5.5.3.3. Относительные деформации крайнего сжатого волокна бетона cс и крайнего растянутого стержня продольной арматуры s в сечении с трещиной в общем случае следует определять из решения расчетной системы уравнений деформационной модели от действия момента, вызванного расчетными усилиями для предельных состояний второй группы. Значения cс и s допускается определять по формулам: cс s cс Ec,red , s Es , (8.21) (8.22) где cс — напряжение в крайнем сжатом волокне бетона в сечении с трещиной; s — напряжение в крайнем растянутом стержне продольной арматуры в сечении с трещиной. Значения cс и s допускается определять из условно упругого расчета сечения с трещиной, нормального к продольной оси, включающего сжатую зону бетона с приведенным модулем упругости Ec,red, сжатую и растянутую арматуру с модулем упругости Es. Для изгибаемых элементов прямоугольного, таврового и двутаврового сечений с арматурой, сосредоточенной у растянутой и сжатой граней сечения, и усилиями, действующими в плоскости симметрии сечения, значения cс и s допускается определять по формулам: cс MSd Acс z , (8.23) s MSd As z , (8.24) где Acc — площадь сжатого бетона в сечении с трещиной; As — площадь растянутой арматуры в сечении с трещиной; z — расстояние между центрами тяжести площади сжатого бетона и растянутой арматуры. Значения Acc и z допускается определять из расчета изгибаемых элементов по предельным усилиям в сечении, нормальном к продольной оси. Кривизну железобетонного элемента (1 r )cr в этом случае следует определять по формуле (8.19), принимая значение d = z. 12.Определение кривизны железобетонных элементов с трещинами Как было показано выше, в элементе с трещинами изгибная жёсткость изменяется по длине элемента. При этом ощутимое отличие в изгибных жесткостях может наблюдаться даже в соседних сечениях. Изменение изгибных жесткостей BII по длине железобетонного элемента, работающего с трещинами, схематично показано на рисунке 102.2. Учёт фактических функций изменения жёсткости по длине пролёта элемента в уравнении (4) существенно усложняет расчёт прогибов. В инженерных расчётах прибегают к определённым упрощениям, которые основываются главным образом на усреднении жесткостей сечений на участке между трещинами и жёсткости в сечениях, проходящих через трещину (штриховая линия на рисунке 102.1). Ещё большим упрощением является усреднение жёсткости по длине элемента. При определении кривизны железобетонного элемента с трещинами используется двухфазовая расчётная модель профессора В.И. Мурашёва, схематически показанная на рисунке 102.2. Рисунок 102.1 — К определению кривизны элемента с трещинами в растянутой зоне. Для получения исходного выражения кривизны рассмотрим участок железобетонного элемента с трещинами в растянутой зоне (рисунок 102.2). Как следует из схемы, показанной на рисунке 102.2 Δlc=εcm*Srm/2 — укорочение бетона в крайнем сжатом волокне сжатой зоны на дине участка Srm/2, а Δls=εsm*Srm/2 — удлинение растянутой арматуры на том же участке Srm/2 (εcm и εsm — средние относительные деформации соответственно крайнего сжатого волокна бетона и растянутой арматуры). Из подобия треугольников АВС и DOF, принимая во внимание разные знаки относительных деформаций удлинения и укорочения, получаем: Srm sm cm Srm , 2r 2d или l sm cm sm cm r d d (1,13) Таким образом, для участков элемента, где в растянутой зоне имеются трещины, нормальные к продольной оси элемента, кривизна определяется как отношение разности средних относительных деформаций крайнего сжатого волокна бетона и продольной растянутой арматуры к рабочей высоте сечения. Задача сводится к вычислению средних относительных деформаций εcm и εsm от усилий, действующих в сечении при заданной нагрузке. Средние относительные деформации в растянутой арматуре и сжатом бетоне определяют в соответствии с положениями, изложенными в главе 10, с учётом «эффекта ужесточения при растяжении» (tension stiffening effect). Как было показано ранее, относительные деформации растянутой арматуры равны: sm sll l sl , (2) где s и s — соответственно относительные деформации растянутой арматуры в стадии l и стадии ll напряжённо деформированного состояния; ξ — коэффициент, учитывающий «эффект ужесточения при растяжении». Идентичным способом можно записать и средние относительные деформации наиболее сжатого волокна бетона: cm cll l cl , (3) l ll где c и c — соответственно относительные деформации наиболее сжатой грани бетона в стадии l и стадии ll напряжённо деформированного состояния. Зная величину средних относительных деформаций в растянутой арматуре и сжатом бетоне, среднюю кривизну элемента в стадии II напряжённо-деформированного состояния (с учётом работы бетона на участках между трещинами (TS)) определяют по формуле: l ll ll l ll l sm cm s l s c l c l m ll l l . r d d m (4) l l — r l кривизна элемента, работающего без трещин в стадии I напряжённо- деформированного, определяемая по формуле: sl cl l . d l ll — r ll (5) кривизна элемента, работающего с трещинами в стадии II напряжённо- деформированного состояния (без учёта работы бетона на участках между трещинами), определяемая: sll cll ll . d (6) 13.Модели, применяемые в расчётах для определения кривизны элементов. Точные методы расчёта требуют учёта многих параметров, влияющих на деформации и напряжения, что в конечном итоге влияет на кривизну элемента. Эти параметры зависят не только от уровня напряжений и свойств материала, а так же наличия или отсутствия трещин, но и от длительности действия нагрузки и способа её приложения. В соответствии с положением линейной теории упругости, кривизна деформируемого элемента зависит от действия изгибающего 1 M момента и может быть определена как: f Sd , r B где: r – радиус кривизны деформированного тела; B – изгибная жёсткость. В результате образования трещин в сечении ж/б элемента происходит перераспределение напряжений в растянутой арматуре, что приводит к возрастанию кривизны и изменению жёсткости на участке между трещинами. В связи с этим существует ряд моделей для определения погибов. I Модель. Наиболее простое выполнение линейной зависимости между изгибающими моментами и кривизной. Модель применяется для определения деформаций в элементах, работающих без трещин при действии кратковременной (1) и длительной (2) нагрузках. II Модель. Двухфазовая расчётная модель базируется на теории Муратова, и позволяет рассчитать прогиб для элементов работающих с трещинами. Используется в нормах. Зависимость между моментом и кривизной представляется ломаной линией, состоящей из линейного участка (1) и ломаного (3) – после образования трещин. Ломаная линия (3) смещается влево по отношению к прямой (2), представляющей изменение кривизны элемента для с трещиной. Мерой смещения ломаной линии (3) по отношению к линии (2) является катет ξ, выражающий эффект совместной работы арматуры и бетона на участке между трещинами. (Эффект ужесточения при растяжении). III Модель. Экспериментально-теоретическая. В ней принято континуально (непрерывно) зависимость между изгибающими моментами и кривизной, вплоть до достижения предельного момента. M u 14.Требования, исходя из которых, нормами установлены предельно допустимые прогибы. Условие проверки деформаций в общем виде. Пояснить значения, входящие в это условие Ограничение по прогибу связанно с необходимостью нормальной эксплуатации зданий и сооружений. Предельно допустимые прогибы установлены из следующих требований: 1 – технологических – обеспечение условий нормальной эксплуатации технологического и подъёмно-транспортного оборудования; 2 – конструктивных – обеспечение целостности притыкаемых друг к другу конструктивных элементов, их стыков, обеспечение требуемых уклонов; 3 – функциональных – предотвращение вредных воздействий и ощущений дискомфорта при колебаниях; 4 – эстетических, психологических – обеспечение благоприятных впечатлений от внешнего вида и предотвращение чувства опасности. Каждое из указных требований должно быть выполнено независимо друг от друга В соответствии с требованиями расчёта конструкций по второй группе предельных состояний при расчёте по деформациям выполняется проверка: ak alim , где: ak ak ,m ak ,v – расчётный прогиб (перемещение) ж/б конструкции от действия внешней нагрузки; alim – предельно допустимый прогиб (перемещение) установленный согласно СНиП «Нагрузки и воздействии» гл.10; ak , m – прогиб обусловленный деформациями изгиба; ak ,v – прогиб обусловленный деформациями сдвига. 15.Определение изгибной жесткости железобетонного элемента, работающего с трещинами по СНБ 5.03.01–02. График распределения изгибных жесткостей по длине железобетонного элемента с трещинами. Изгибную жесткость элемента с трещинами в общем случае следует определять по формуле Bm,cr MSd (1 r )cr . (8.25) Допускается определять изгибную жесткость железобетонного элемента с трещинами B , t0 по формуле B , t0 Ec,eff III 2 I 1 1 2 sr 1 II II s , (8.26) где Ec,eff — эффективный модуль упругости бетона; III , II — соответственно момент инерции сечения с трещиной и без трещины, определяемый с учетом отношения e Es Ec ,eff . Значения эффективного модуля упругости бетона Ec,eff определяются: — при действии кратковременной нагрузки Ec,eff = Ecm ; (8.27) — при действии длительной нагрузки Ec,eff Ecm , 1 (, t0 ) (8.28) где (,t0) — предельное значение коэффициента ползучести для бетона, определяемое в соответствии с указаниями раздела 6. 16. Определение ak,v по СНБ 5.03.01–02. Понятие деформации сдвига. В общем случае прогиб ЖБ конструкций следует определять: Где ak,m – прогиб, обусловленный деформациями изгиба ak,v – прогиб, обусловленный деформациями сдвига Значение ak,v следует определять: Где Ṽ - поперечная сила в сечении х, определяемая от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяется прогиб; γ (x) — деформация сдвига в сечении х от нагрузки, при которой определяется прогиб; VSd(x)— поперечная сила в сечении х от нагрузки, при которой определяется прогиб; Bv(x) — сдвиговая жесткость железобетонного элемента в сечении х. Определение деформации сдвига и сдвиговой жесткости Сдвиговую жесткость допускается определять по формуле: где Gc - модуль сдвига бетона, принимаемый равным 0,4Ecm; φcr(x)— коэффициент, учитывающий влияние трещин на деформацию сдвига. Деформации сдвига допускается определять по формуле: где VSd(x) расчетная поперечная Bv(x) - сдвиговая жесткость в сечении x. сила в сечении x; 17.Величина Srm (понятие величин входящих в формулу определения Srm). Среднее расстояние srm между трещинами, мм, нормальными к продольной оси, в изгибаемых и растянутых элементах следует определять по формуле srm 50 0,25k1 k2 eff , ( 8.7) где — диаметр стержня, мм, (при использовании в одном сечении стержней разных диаметров допускается принимать в формуле (8.7) их средний диаметр); k1 — коэффициент, учитывающий условия сцепления арматуры с бетоном, равный: для стержней периодического профиля k1 = 0,8; для гладких стержней k1 = 1,6; k2 — коэффициент, учитывающий вид напряженнодеформированного состояния элемента (рисунок 8.1) и принимаемый равным: при изгибе k2 = 0,5; при осевом растяжении k2 = 1,0; при внецентренном растяжении: если 1 > 2 k2 1 2 21 ; (8.8) если 2 = 0 k2 = 0,5 ; eff — эффективный коэффициент армирования, определяемый для железобетонных элементов по формуле eff As Ac ,eff , здесь As — площадь сечения арматуры, заключенной внутри эффективной площади растянутой зоны сечения Ac,eff ; Ac,eff — эффективная площадь растянутой зоны сечения, определяемая в общем случае как площадь бетона, окружающего растянутую арматуру при высоте, равной 2,5 расстояния от наиболее растянутой грани до центра тяжести арматуры (рисунок 8.2 Для элементов, в которых высота растянутой зоны может быть значительной, высота эффективной площади растянутой зоны принимается не более (h - х)/3. k2 1 2 k2 = 1,0 k2 = 0,5 k2 = 0,5 21 Рисунок 8.1 — К определению коэффициента k2 в формуле (8.7) Рисунок 8.2 — К определению эффективной площади растянутой зоны сечения Ac,eff : а — балки; б — плиты; 1 18.Какую величину определяют по формуле: ... M ( x) 0 1 dx r ( x) , пояснить значения, входящие в формулу. В соответствии с требованиями расчёта конструкций по второй группе предельных состояний при расчёте по деформациям выполняется проверка: ak alim , где: ak ak ,m ak ,v – расчётный прогиб (перемещение) ж/б конструкции от действия внешней нагрузки; alim – предельно допустимый прогиб (перемещение) установленный согласно СНиП «Нагрузки и воздействии» гл.10; где ak,m— прогиб, обусловленный деформациями изгиба; ak,v — прогиб, обусловленный деформациями сдвига. Значения ak,m определяют по формулам: l 1 dx r (x) , (8.14) MSd ( x ) dx , Bm ( x ) (8.15) ak ,m M ( x ) 0 l ak ,m M ( x ) 0 где M ( x ) — изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяют прогиб; 1 — кривизна элемента в сечении х от расчетного сочетания r (x) внешних нагрузок, при которой определяется прогиб; MSd(x) — изгибающий момент в сечении х от расчетного сочетания внешних нагрузок, при которой определяется прогиб; Bm(x) — изгибная жесткость железобетонного элемента в сечении х. Ограничение по прогибу связанно с необходимостью нормальной эксплуатации зданий и сооружений. Предельно допустимые прогибы установлены из следующих требований: 1 – технологических – обеспечение условий нормальной эксплуатации технологического и подъёмно-транспортного оборудования; 2 – конструктивных – обеспечение целостности притыкаемых друг к другу конструктивных элементов, их стыков, обеспечение требуемых уклонов; 3 – функциональных – предотвращение вредных воздействий и ощущений дискомфорта при колебаниях; 4 – эстетических, психологических – обеспечение благоприятных впечатлений от внешнего вида и предотвращение чувства опасности. Каждое из указных требований должно быть выполнено независимо друг от друга. 19. Понятие и особенности определения ψs. Значение средней относительной деформации растянутой арматуры sm следует определять по формуле sm = ss , (8.9) где s — относительная деформация растянутой арматуры в сечении с трещиной, определяемая в общем случае из решения расчетной системы уравнений деформационной модели от действия изгибающего момента и продольной силы в соответствии с 5.5.3.2; s —коэффициент, учитывающий неравномерность распределения относительных деформаций растянутой арматуры на участках между трещинами, величину которого следует определять по формуле 2 s 1 1 2 sr , s (8.10) здесь s — напряжения в растянутой арматуре, рассчитанные для сечения с трещиной, от усилий, вызванных расчетным сочетанием нагрузок; sr — напряжения в растянутой арматуре, рассчитанные для сечения с трещиной, от усилий, при которых образуются трещины; 1 — коэффициент, принимаемый равным: для стержневой арматуры периодического профиля — 1,0; для гладкой стержневой арматуры — 0,5; 2 — коэффициент, учитывающий длительность действия нагрузки, принимаемый равным: при действии кратковременных нагрузок — 1,0; при действии длительно действующих и многократно повторяющихся нагрузок — 0,5. В формуле (8.10) вместо отношения sr s допускается принимать: — при осевом растяжении — Ncr NSd ; — при изгибе — Mcr MSd . Усилия трещинообразования допускается определять как для бетонного сечения по формулам: Mcr = fctmWc , Ncr = fctmAc , где fctm — средняя прочность бетона при растяжении, принимаемая по таблице 6.1. Расчетное продольное усилие NSd и изгибающий момент MSd следует определять для соответствующего сочетания нагрузок при F = 1,0. Для элементов, трещинообразование которых вызвано действием только вынужденных деформаций, в формуле (8.10) допускается принимать s = sr. Ширину раскрытия трещин wk для расчетных ситуаций, когда растягивающие напряжения вызваны совместным действием вынужденных деформаций и усилий от внешних нагрузок, следует определять по формуле (8.6). В этом случае к относительным деформациям арматуры, рассчитанным для сечения с трещиной от действующих усилий, вызванных нагрузкой, следует суммировать вынужденные деформации. wk = srmsm , (8.6) где srm — среднее расстояние между трещинами; sm — средние относительные деформации арматуры, определяемые при соответствующем сочетании нагрузок; — коэффициент, учитывающий отношение расчетной ширины раскрытия трещин к средней. Для изгибаемых элементов с большим расстоянием между продольными стержнями при расчете ширины раскрытия трещин можно принимать sr,max = 1,3(h x), где h — полная высота сечения, а х — высота сжатой зоны. 20.Определение изгибной жесткости железобетонного элемента, работающего без трещин (формулы, пояснить значения, входящие в эти формулы). Изгибную жесткость железобетонного элемента без трещин B , t0 следует определять по формуле (8.26), принимая III = II, значение эффективного модуля упругости бетона Ec,eff 1 по формуле (8.27) или (8.28), а кривизну r по формуле MSd 1 r B (, t ) . m 0 B , t0 (8.30) Ec,eff III 2 I , 1 1 2 sr 1 II II s (8.26) где Ec,eff — эффективный модуль упругости бетона; III , II — соответственно момент инерции сечения с трещиной и без E s e трещины, определяемый с учетом отношения Ec,eff . Значения эффективного модуля упругости бетона Ec,eff определяются: — при действии кратковременной нагрузки Ec,eff = Ecm ; (8.27) — при действии длительной нагрузки Ec,eff Ecm 1 (, t0 ) , (8.28) где (,t0) — предельное значение коэффициента ползучести для бетона, определяемое в соответствии с указаниями раздела 6. 21. Понятие wlim. Обстоятельства, обуславливающие wlim. Понятие wk. Формула определения wk по СНБ 5.03.01-02. Пояснить значения, входящие в формулу. Трещиностойкость железобетонной конструкции – её способность сопротивляться образованию и раскрытию трещин. Расчеты по образованию и ширине раскрытия трещин относятся к расчетам по предельным состояниям второй группы, обеспечивающей нормальные условия эксплуатации конструкций. Расчет по раскрытию трещин следует производить из условия wk ≤ wlim wlim – предельно допустимая ширина раскрытия трещин. wlim определяется по таблице 5.1 СНБ 5.03.01-02 в зависимости от класса по условиям эксплуатации, а также в зависимости от того, является ли железобетонная конструкция предварительно напряженной (для преднапряженных Wlim меньше). Класс по условиям Железобетонные элементы Предварительно эксплуатации напряженные элементы Практически постоянное Частое сочетание нагрузок сочетание нагрузок по по приложению А Х0, ХС1 ХС2, ХС3, ХС4 XA1,XA2,XD1,XD2 приложению А 0,4 0,3 По СНиП 0,2 0,2* Не допускается * Для этих классов по условиям эксплуатации при действии практически постоянного сочетания нагрузок должно выполняться условие декомпрессии (отсутствие растягивающих напряжений в бетоне на уровне напрягаемой арматуры). wk – расчетная ширина раскрытия трещин, нормальных к продольной оси. Принимается по формуле wk = β·srm·εsm srm – среднее расстояние между трещинами; εsm – средние относительные деформации арматуры, определяемые при соответствующем сочетании нагрузок; β – коэффициент, учитывающий отношение расчетной ширины раскрытия трещин к средней. β = 1,7 – при расчете ширины раскрытия трещин, образующихся от усилий, вызванных соответствующим сочетанием нагрузок, а также от усилий, возникающих при ограничении вынужденных деформаций для сечений, наименьший размер которых (высота, ширина, толщина) превышает 800 мм; β = 1,3 – при расчете ширины раскрытия трещин, образующихся от действия усилий, возникающих при ограничении вынужденных деформаций для сечений, наименьший размер которых (высота, ширина, толщина) составляет 300 мм и менее. При расчете ширины раскрытия трещин, образующихся от усилий, вызванных ограничением вынужденных деформаций, для промежуточных размеров сечения элемента значения коэффициента допускается определять по линейной интерполяции. ⌀ - диаметр стержня, vv k1 – коэффициент, учитывающий условия сцепления арматуры с бетоном, равный: для стержней периодического профиля k1 = 0,8; для гладких стержней k1 = 1,6; k2 – коэффициент, учитывающий вид напряженно-деформированного состояния элемента – эффективный коэффициент армирования εsm = εs ·Ψs εs – относительная деформация растянутой арматуры в сечении с трещиной Ψs – коэффициент, учитывающий неравномерность распределения относительных деформаций растянутой арматуры на участках между трещинами. 22.Упрощенный способ определения сс и s по СНБ 5.03.01–02 при определении кривизны железобетонного элемента, работающего с трещинами. Определение кривизны и изгибной жесткости железобетонных конструкций.Кривизну железобетонных элементов (или участков элементов) с трещинами 1 , нормальными к продольной оси, следует определять по формуле r cr cm sm,0 1 r d cr , где cm — средние относительные деформации крайнего сжатого волокна бетона на участке между трещинами; sm,0 — средние относительные деформации крайнего растянутого стержня продольной арматуры на участке между трещинами; d — расстояние между крайним сжатым волокном бетона и крайним растянутым стержнем продольной арматуры. Значение cm определяют по формуле cm c cc , где cс — относительная деформация крайнего сжатого волокна бетона в сечении с трещиной; с — коэффициент, учитывающий неравномерность распределения относительных деформаций сжатого бетона между трещинами. Значение коэффициента допускается принимать равным 0,9. Относительные деформации крайнего сжатого волокна бетона cс и крайнего растянутого стержня продольной арматуры s в сечении с трещиной в общем случае следует определять из решения расчетной системы уравнений деформационной модели от действия момента, вызванного расчетными усилиями для предельных состояний второй группы. Значения cс и s допускается определять по формулам: cс cс Ec,red , s s Es , где cс — напряжение в крайнем сжатом волокне бетона в сечении с трещиной; s — напряжение в крайнем растянутом стержне продольной арматуры в сечении с трещиной. Для изгибаемых элементов прямоугольного, таврового и двутаврового сечений с арматурой, сосредоточенной у растянутой и сжатой граней сечения, и усилиями, действующими в плоскости симметрии сечения, значения cс и s допускается определять по формулам: cс MSd , s MSd , Acс z As z где Acc — площадь сжатого бетона в сечении с трещиной; As — площадь растянутой арматуры в сечении с трещиной; z — расстояние между центрами тяжести площади сжатого бетона и растянутой арматуры. 23.Упрощенный способ определения прогибов при изгибе по СНБ 5.03.01–02 для элементов прямоугольного, таврового и двутаврового сечений. Для железобетонных элементов прямоугольного, таврового и двутаврового сечений с арматурой, сосредоточенной у верхней и нижней граней, и усилиями, действующими в плоскости симметрии сечения, допускается определять прогиб при изгибе a(,t0) по упрощенной формуле a(, t0 ) k 2 MSd leff B(, t0 ) , где k — коэффициент, зависящий от способа приложения нагрузки и схемы опирания элемента; MSd — максимальное значение расчетного момента по предельным состояниям второй группы; B(,t0) — изгибная жесткость элемента, определяемая при длительном действии нагрузки по формуле. Допускается определять изгибную жесткость железобетонного элемента с трещинами B , t0 по формуле B , t0 Ec,eff III 2 I 1 1 2 sr 1 II II s , (8.26) где Ec,eff — эффективный модуль упругости бетона; III , II — соответственно момент инерции сечения с трещиной и без трещины, определяемый с учетом отношения e Es Ec ,eff . Значения эффективного модуля упругости бетона Ec,eff определяются: — при действии кратковременной нагрузки Ec,eff = Ecm ; — при действии длительной нагрузки Ec,eff Ecm , 1 (, t0 ) (8.27) (8.28) где (,t0) — предельное значение коэффициента ползучести для бетона, определяемое в соответствии с указаниями раздела 6. 24.Определение прогибов железобетонных элементов а) общий метод упрощенный метод. б) В общем случае прогиб железобетонных конструкций следует определять по формуле: ak = ak,m + ak,v , где ak,m — прогиб, обусловленный деформациями изгиба; ak,v — прогиб, обусловленный деформациями сдвига. Значения ak,m определяют по формулам: l ak ,m M ( x ) 0 где 1 r (x) M( x ) l M (x) 1 dx , ak ,m M ( x ) Sd dx , r (x) Bm ( x ) 0 — изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяют прогиб; — кривизна элемента в сечении х от расчетного сочетания внешних нагрузок, при которой определяется прогиб; MSd(x) — изгибающий момент в сечении х от расчетного сочетания внешних нагрузок, при которой определяется прогиб; Bm(x) — изгибная жесткость железобетонного элемента в сечении х. Значение ak,v определяют по формулам: l l 0 0 ak ,v V ( x ) ( x ) dx , ak ,v V ( x ) где VSd ( x ) dx , Bv ( x ) — поперечная сила в сечении х, определяемая от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяется прогиб; (x) — деформация сдвига в сечении х от нагрузки, при которой определяется прогиб; VSd(x) — поперечная сила в сечении х от нагрузки, при которой определяется прогиб; Bv(x)— сдвиговая жесткость железобетонного элемента в сечении х. Для железобетонных элементов прямоугольного, таврового и двутаврового сечений с арматурой, сосредоточенной у верхней и нижней граней, и усилиями, действующими в плоскости симметрии сечения, допускается определять прогиб при изгибе a(,t0) по упрощенной формуле V (x) a(, t0 ) k 2 MSd leff B(, t0 ) , где k— коэффициент, нагрузки и схемы опирания элемента; зависящий о приложения — максимальное значение расчетного момента по предельным состояниям второй группы; B(,t0) — изгибная жесткость элемента, определяемая при длительном действии нагрузки по формуле (8.26). MSd 25.Определение кривизны ж/б элемента (без трещин)с учетом усадочных деформаций бетона по СНБ 5.03.01–02. Пояснить значения, входящие в формулу. Кривизна от усадки бетона: Дополнительную кривизну от неравномерной усадки бетона 1 r следует cs определять по формуле cs, e S 1 , r I cs где cs, — предельное значение усадки бетона; S — статический момент арматуры относительно центра тяжести сечения; I — момент инерции сечения; e Es Ec,eff , Ec,eff Ecm . 1 , t0 Предельное значение коэффициента ползучести для бетона ,t0 При расчете кривизны от усадки для элементов с трещинами значения S и I определяют дважды: для сечения без трещины и сечения с трещиной. Окончательное значение кривизны 1 r в cs этом случае определяют из формулы : s II 1 s I , где — анализируемый параметр, в качестве которого могут рассматриваться кривизна, угол поворота или прогиб; I , II — соответственно значения параметра, определенные для сечения без трещины и с трещиной; s — коэффициент, учитывающий неравномерность распределения относительных деформаций растянутой арматуры на участках между трещинами, величину которого следует определять по формуле 26. Расчетные модели, используемые для определения прогибов зависимости). Расчётные модели, принимаемы при определении прогибов. (графики, Точные методы расчёта требуют учёта многих параметров, влияющих на деформации и напряжения, что в конечном итоге влияет на кривизну элемента. Эти параметры зависят не только от уровня напряжений и свойств материала, а так же наличия или отсутствия трещин, но и от длительности действия нагрузки и способа её приложения. В соответствии с положением линейной теории упругости, кривизна деформируемого элемента зависит от действия 1 M Sd , r B где: r – радиус кривизны деформированного тела; B – изгибная жёсткость. изгибающего момента и может быть определена как: f В результате образования трещин в сечении ж/б элемента происходит перераспределение напряжений в растянутой арматуре, что приводит к возрастанию кривизны и изменению жёсткости на участке между трещинами. В связи с этим существует ряд моделей для определения погибов. I Модель. Наиболее простое выполнение линейной зависимости между изгибающими моментами и кривизной. Модель применяется для определения деформаций в элементах, работающих без трещин при действии кратковременной (1) и длительной (2) нагрузках. II Модель. Двухфазовая расчётная модель базируется на теории Муратова, и позволяет рассчитать прогиб для элементов работающих с трещинами. Используется в нормах. Зависимость между моментом и кривизной представляется ломаной линией, состоящей из линейного участка (1) и ломаного (3) – после образования трещин. Ломаная линия (3) смещается влево по отношению к прямой (2), представляющей изменение кривизны элемента для с трещиной. Мерой смещения ломаной линии (3) по отношению к линии (2) является катет ξ, выражающий эффект совместной работы арматуры и бетона на участке между трещинами. (Эффект ужесточения при растяжении). III Модель. Экспериментально-теоретическая. В ней принято континуально (непрерывно) зависимость между изгибающими моментами и кривизной, вплоть до достижения предельного момента. M u Второй вариант шпоры!!! 27. Определение ak,v по СНБ 5.03.01–02. Понятие деформации сдвига, сдвиговой жесткости. В общем случае прогиб железобетонных конструкций следует определять по формуле ak = ak,m + ak,v , ak,v (8.13) где ak,m — прогиб, обусловленный деформациями изгиба; — прогиб, обусловленный деформациями сдвига. Значения ak,m определяют по формулам: l ak ,m M ( x ) 0 l ak ,m M ( x ) 0 1 dx , r (x) (8.14) MSd ( x ) dx , Bm ( x ) (8.15) где M ( x ) — изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяют прогиб; 1 — кривизна элемента в сечении х от расчетного сочетания внешних нагрузок, при r (x) которой определяется прогиб; MSd(x) — изгибающий момент в сечении х от расчетного сочетания внешних нагрузок, при которой определяется прогиб; Bm(x) — изгибная жесткость железобетонного элемента в сечении х. Значение ak,v определяют по формулам: l ak ,v V ( x ) ( x ) dx , (8.16) 0 l ak ,v V ( x ) 0 VSd ( x ) dx , Bv ( x ) (8.17) где V ( x ) — поперечная сила в сечении х, определяемая от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяется прогиб; (x) — деформация сдвига в сечении х от нагрузки, при которой определяется прогиб; VSd(x) — поперечная сила в сечении х от нагрузки, при которой определяется прогиб; Bv(x) — сдвиговая жесткость железобетонного элемента в сечении х. Деформация сдвига возникает в тех случаях, когда внешние силы, действующие на брус, расположены в параллельных плоскостях на очень малом расстоянии друг от друга и направлены в противоположные стороны. 8.3.4.1 Сдвиговую жесткость допускается определять по формуле Bv ( x ) 2 cr ( x ) Gc b h , 3 (8.32) где Gc — модуль сдвига бетона, принимаемый равным 0,4Ecm; cr(x) — коэффициент, учитывающий влияние трещин на деформацию сдвига. 8.3.4.2 Деформации сдвига допускается определять по формуле v (x) где VSd(x) VSd ( x ) , Bv ( x ) — расчетная поперечная сила в сечении x; (8.33) Bv(x) — сдвиговая жесткость в сечении x. 28. Какая величина определяется по формуле: ... 50 0,25 k1 k 2 eff , пояснить значения, входящие в эту формулу. Среднее расстояние srm между трещинами, мм, нормальными к продольной оси, в изгибаемых и растянутых элементах следует определять по формуле srm 50 0,25k1 k2 k1 eff , ( 8.7) где — диаметр стержня, мм, (при использовании в одном сечении стержней разных диаметров допускается принимать в формуле (8.7) их средний диаметр); — коэффициент, учитывающий условия сцепления арматуры с бетоном, равный: для стержней периодического профиля k1 = 0,8; для гладких стержней k1 = 1,6; k2 — коэффициент, учитывающий вид напряженно-деформированного состояния элемента (рисунок 8.1) и принимаемый равным: при изгибе k2 = 0,5; при осевом растяжении k2 = 1,0; при внецентренном растяжении: если 1 > 2 k2 1 2 ; 21 (8.8) если 2 = 0 k2 = 0,5 ; eff — эффективный коэффициент армирования, определяемый для железобетонных элементов по формуле eff здесь As Ac,eff As Ac ,eff , — площадь сечения арматуры, заключенной внутри эффективной площади растянутой зоны сечения Ac,eff ; — эффективная площадь растянутой зоны сечения, определяемая в общем случае как площадь бетона, окружающего растянутую арматуру при высоте, равной 2,5 расстояния от наиболее растянутой грани до центра тяжести арматуры (рисунок 8.2 Для элементов, в которых высота растянутой зоны может быть значительной, высота эффективной площади растянутой зоны принимается не более (h - х)/3. k2 = 1,0 k2 = 0,5 k2 1 2 21 k2 = 0,5 Рисунок 8.1 — К определению коэффициента k2 в формуле (8.7) 2 29. Какая величина определяется по формуле ... cr ( x) Gc b h , пояснить 3 значения, входящие в формулу. Сдвиговую жесткость допускается определять по формуле 2 Bv ( x ) cr ( x ) Gc b h , 3 где Gc — модуль сдвига бетона, принимаемый равным 0,4Ecm; cr(x) — коэффициент, учитывающий влияние трещин на деформацию сдвига. b – ширина сечения h – высота сечения. (8.32) 30. Как определить ak по СНБ 5.03.01–02. Пояснить значения, входящие в формулу. В общем случае прогиб железобетонных конструкций следует определять по формуле ak = ak,m + ak,v , ak,v (8.13) где ak,m — прогиб, обусловленный деформациями изгиба; — прогиб, обусловленный деформациями сдвига. Значения ak,m определяют по формулам: l ak ,m M ( x ) 0 l ak ,m M ( x ) 0 1 dx , r (x) (8.14) MSd ( x ) dx , Bm ( x ) (8.15) где M ( x ) — изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяют прогиб; 1 — кривизна элемента в сечении х от расчетного сочетания внешних нагрузок, при r (x) которой определяется прогиб; MSd(x) — изгибающий момент в сечении х от расчетного сочетания внешних нагрузок, при которой определяется прогиб; Bm(x) — изгибная жесткость железобетонного элемента в сечении х. Значение ak,v определяют по формулам: l ak ,v V ( x ) ( x ) dx , (8.16) 0 l ak ,v V ( x ) 0 VSd ( x ) dx , Bv ( x ) (8.17) где V ( x ) — поперечная сила в сечении х, определяемая от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяется прогиб; (x) — деформация сдвига в сечении х от нагрузки, при которой определяется прогиб; VSd(x) — поперечная сила в сечении х от нагрузки, при которой определяется прогиб; Bv(x) — сдвиговая жесткость железобетонного элемента в сечении х. 31. Величина sm . Как определить sm по СНБ 5.03.01–02. (пояснить значения, входящие в формулу). sm — средние относительные деформации арматуры, определяемые при соответствующем сочетании нагрузок; Значение средней относительной деформации растянутой арматуры sm следует определять по формуле sm = ss , (8.9) где s — относительная деформация растянутой арматуры в сечении с трещиной, определяемая в общем случае из решения расчетной системы уравнений деформационной модели от действия изгибающего момента и продольной силы в соответствии с 5.5.3.2; s — коэффициент, учитывающий неравномерность распределения относительных деформаций растянутой арматуры на участках между трещинами, величину которого следует определять по формуле 2 sr , (8.10) s s 1 1 2 здесь s — напряжения в растянутой арматуре, рассчитанные для сечения с трещиной, от усилий, вызванных расчетным сочетанием нагрузок; sr — напряжения в растянутой арматуре, рассчитанные для сечения с трещиной, от усилий, при которых образуются трещины; 1 — коэффициент, принимаемый равным: для стержневой арматуры периодического профиля — 1,0; для гладкой стержневой арматуры — 0,5; 2 — коэффициент, учитывающий длительность действия нагрузки, принимаемый равным: при действии кратковременных нагрузок — 1,0; при действии длительно действующих и многократно повторяющихся нагрузок — 0,5. В формуле (8.10) вместо отношения sr s допускается принимать: — при осевом растяжении — Ncr NSd ; — при изгибе — Mcr MSd . Усилия трещинообразования допускается определять как для бетонного сечения по формулам: Mcr = fctmWc , Ncr = fctmAc , где fctm — средняя прочность бетона при растяжении, принимаемая по таблице 6.1. Расчетное продольное усилие NSd и изгибающий момент MSd следует определять для соответствующего сочетания нагрузок при F = 1,0. Для элементов, трещинообразование которых вызвано действием только вынужденных деформаций, в формуле (8.10) допускается принимать s = sr. Ширину раскрытия трещин wk для расчетных ситуаций, когда растягивающие напряжения вызваны совместным действием вынужденных деформаций и усилий от внешних нагрузок, следует определять по формуле (8.6). В этом случае к относительным деформациям арматуры, рассчитанным для сечения с трещиной от действующих усилий, вызванных нагрузкой, следует суммировать вынужденные деформации. Для изгибаемых элементов с большим расстоянием между продольными стержнями при расчете ширины раскрытия трещин можно принимать sr,max = 1,3(h x), где h — полная высота сечения, а х — высота сжатой зоны. 32. Компоновка конструктивной схемы ОПЗ В ходе компановки решаются следующие вопросы: 1. определение характерных габаритов, наличие навесных или мостовых кранов или другого подвесного оборудования; 2. назначается сетка и размеры; (6x12; 12x12; 6x18; 12x18; 6x42; 12x24; 12x32) 3. определяется типы привязки; 4. определяется высота здания; 5. выполняется компановка покрытия; 6. разбивка здания на температурные блоки; 7. выбор схемы связей, обеспечивающих пространственную жесткость каркаса. Рис. Конструктивная схема здания со скатной кровлей при шаге колонн 6 (12) м. 1 – колонна; 2 – стропильная ферма (раскосная или безраскосная); 3 – фонарь; 4 – стальные связи; 5 – стальная распорка; 6 – плита покрытия длиной 6 (12) м. Колонны классифицируются: по назначению: основные; фахверковые. в зависимости от расположения: крайнего ряда; средние. от формы поперечного сечения: от размеров по длине колонны: постоянного сечения по длине колонны; ступенчатого сечения. Так же колонны могут быть: одноветвевые; двухветвевые. Привязка: При крановых нагрузках(до 30 т) и шаге колонн 6м и высоте не выше 14,4 м применяется «нулевая привязка». При грузоподьемности крана >30 т, шаге колонн 12 м и Н>14,4 м исп. привязка «250». а) и б) - в крайних продольных рядах здания; в) и г) - в торцах здания. Рис. Привязки колонн крайних рядов а) – привязка колонн средних рядов; б) основная привязка парных колонн в поперечных температурных швах; в) - допускаемая привязка парных колонн в поперечных температурных швах. Рис. Привязки колонн средних рядов Расстояние между разбивочными осями и осями подкрановых балок: при грузоподъемности крана Q<=15 т – l=500 мм при грузоподъемности крана Q<=50 т – l=750 мм при грузоподъемности крана Q>50 т – l=1000 мм Определение высоты здания: Высота здания определяется с учетом технологических процессов: зрузоподъемность кранового оборудования и габаритов крана; от размещения стеновых панелей и оконных переплетов; от типа конструкций покрытия; от наличия или отсутствия зенитных фонарей. Окончательно высоту здания назначают из типовых требований так, чтобы отметка верха колонн была кратна 600 мм. Связи ОПЗ Назначение связей: способствуют приданию жесткости покрытия(при высоте балки на опоре h(оп) >900 мм – выполняются связи по стропильным конструкциям); обеспечивают устойчивость сжатых поясов, стоек ферм, опорных частей балок при высоте балки на опоре h(оп)>900 мм; без связи произойдет смещение верха стропильной конструкции; для восприятия ветровых нагрузок торцами здания; восприятние тормозных усилий вдоль здания от действия горизонтальных напряжений, вызванными мостовыми кранами. h(оп)<0,9м Вид здания h(оп)>0,9м Без крана, Н(к)<=10м Без крана, Н(к)>10м Крановое здание Разбивка зданий на температурные блоки. Основное назначение температурно-усадочных швов: для восприятия внутренних усилий к колоннах от внутренних перемещений в продольном и поперечном элементах вследствии переменной температуры наружного воздуха и усадки бетона. Максимальных температурный блок – 72 м(при температуре наружного воздуха до -40 ˚С для отапливаемых зданий); для неотапливаемых – 42 м. Поперечные температурно-усадочные швы выполняются на спаренных колоннах со смещением геометрической оси на 500 мм. При этом шов доводится до фундамента, колонны имеют общий фундамент. Иногда устраивается и продольные температурно-усадочные швы. 33. Конструктивные схемы одноэтажных производственных зданий. 1)по типу покрытия: -балочные (их линейных элементов); -пространственные (оболочки, складки). 2)по типу оборудования: - бескрановое (50%) - с мостовыми кранами (15%) - с подвесными кранами (35%) 3)по пролетам: одно- и многопролетные. 4)по уклону кровли: - плоская - мало уклонная (до 5 %) - уклонная 5)по способу освещения и вентиляции: -здания с зенитными фонарами; -бесфонарные. 6)по высоте здания: -с перепадом высот; -без перепада высот. 7) по способу возведения: -со сборными поперечными рамами; -с монолитными поперечными рамами. 8)по материалу: жб (86%), металл (10%) и дерево (2-4%) Здания, в большинстве случаев, решаются по каркасной схеме. Каркас одноэтажного производственного здания представляет собой пространственную систему, состоящую из защемленных в фундаменты колонн, объединенных (в пределах температурного блока) стропильными и подстропильными конструкциями, плитами, связями и т.д. или покрытием в виде оболочек. Эта пространственная система условно расчленяется на поперечные и продольные плоские рамы. Поперечные рамы образуются из колонн и стропильных конструкций или диафрагм оболочек, продольные – из колонн, плит покрытия или прогонов, подстропильных конструкций, связей (решетчатых и в виде распорок) и подкрановых балок, а также диафрагм или бортовых элементов оболочек. К основным строительным параметрам зданий, подлежащим унификации, относятся: пролет, шаг опор (сетка колонн) и высотные габариты; вид и грузоподъемность подъемно–транспортного оборудования; привязка элементов конструкций к координационным (разбивочным) осям; размеры вставок в местах температурных швов и примыканий у взаимно перпендикулярных пролетов и перепадов высот; уклоны кровель из различных материалов; производственные нагрузки и воздействия. Унификация параметров и конструкций зданий проводится на основе прямоугольной системы модульных координат, обеспечивающей соизмеримость элементов и деталей зданий, кратность их модулю определенной величины, что создает необходимые условия для строительства зданий из заранее изготовленных элементов при их различных сочетаниях. В настоящее время более 95% общей площади промышленных зданий проектируют с применением унифицированных размеров пролета и шага основных несущих конструкций, более 85% общей площади – с унифицированным размером высот. В качестве основного модуля принят модуль М, равный 100 мм. Для координации и согласования размеров и взаимного расположения объемно-планировочных и конструктивных элементов строительных изделий, сантехнического и другого оборудования зданий с размером самого здания применяется оптимальный ряд производственных укрупненных модулей. Градация параметров планировочных и конструктивных элементов устанавливается равной одному из укрупненных модулей. Например, пролеты и шаги колонн одноэтажных зданий и соответствующие им номинальные размеры конструкций покрытия рекомендуется принимать кратными 60М (при пролетах более 12000 мм) или 30М (при пролетах 6000 – 12000 мм). Для размера высот приняты модули, 6М (600 мм) и 12М (1200 мм) в зависимости от типа зданий и их высоты. 34. Классификация колонн ОПЗ. Методы статического расчета Для бескрановых зданий высотой до 9,6 м. сборные колонны имеют пост. сечение; при большей высоте сечение переменное. Для крановых зданий сечение всех колонн переменное, развитое в их подкрановой части. По материалу колонны подразделяют на ж/б и стальные. Ж/б, как правило, сборные; для высоких заний они сост. из двух-трех Элементов, соед. на месте стр-ва на сварке с помощью закладных частей. сечения колонн-400х400, 500х800, двутавровые 400х600, 400х800. двухветвевые от 400х1000 до 600х2400 мм. Конструкция сборных ж/б колонн зависит от объёмнопланировочного решения промышленного здания и наличия в нем того или иного вида подъёмнотранспортного оборудования определённой грузоподъёмности. В связи с этим сборные ж/б колонны подразделяют на 2 группы. Колонны, относящиеся к первой группе, предназначены для зданий без мостовых кранов, в бескрановых цехах и в цехах, оснащенных подвесным подъёмно-транспортным оборудованием. Колонны второй группы применяют в цехах, оборудованных мостовыми кранами. По конструктивному решению колонны разделяют на одноветвевые и двухветвевые, по местоположению в здании - на крайние, средние и располагаемые у торцевых стен. Выбор сечения колонны зависит от размеров пролета и их числа, величины шага колонн, наличие подстропильных конструкций, подвесного транспорта и конструктивного решения покрытия. Колонны каркаса устанавливают в фундаменты стаканного типа и замоноличивают. Для зданий без мостовых кранов, имеющих высоту от пола до низа несущих конструкций покрытия до 9.6 м, применяют колонны сечением 400х400, 500х500и 600х500.Средние колонны сечением 400х400 мм в месте опирания несущих конструкций покрытия имеет со стороны 2-х боков граней консоли. Выбор сечения колонны зависит от размеров пролета и их числа, величины шага колонн, наличия подстропильных конструкций, подвесного транспорта и конструктивного решения покрытия.Колонна для здания, оборудуемого мостовыми кранами состоит из надкрановой и подкрановой частей. Надкрановая часть служит для опирания несущей конструкции покрытия и называется надколодником. Крайние колонны имеют одностороннюю консоль, средние двухсторонние консоли. При Привязка при крановых нагрузках 30 т и шаге колонн 6м, при высоте 14,4 м –нулевая привязка грузоподъемности 30 м, шаге 12 м и высоте 14,4 м – привязка 250мм. Q 15т 500мм Q 50т 750мм Q 50т 1000мм Высота здания определяется с учетом технологических процессов, грузоподъемности кранового оборудования и габаритов крана, от размещения стеновых панелей и оконных проемов, от типа покрытия или отсутствия фонарей. Окончательная высота назначается так чтобы отм. верха колонн была кратна 0,6 м. Методы расчета: по деформируемой схеме по недеформируемой схеме В инженерных расчетах ограничиваются расчетом на все виды воздействий, за исключением вынужденных перемещений по недеформируемой схеме как упругой линейно-деформируемой схемы без учета влияния трещин и неупругих деформаций бетона на кривизну элемента. При этом влияние продольного изгиба учитывают при подборе сечения учетом коэффициента η. Расчет рам в этом случае выполняют методом перемещений. Если необходимо учитывать податливость ригелей, то расчет выполняют методом сил. В результате статического расчета определяется смещение (горизонтальное) рамы, раскрывается статическая неопределимость конструкции, и после чего определяются реакции опор колонны и находятся усилия в её сечении. ПРЦ одного температурного блока связаны между собой плитами покрытия. При этом сборные плиты соединены со стропильными конструкциями при помощи сварки закладных деталей и заливкой швов. Такая конструкция представляет собой жесткую в своей плоскости диафрагму, обеспечивающую совместную работу поперечных рам. 35. Статический расчет ПРЦ. Расчетная схема, определение нагрузок Поперечная одно- или многопролетная рама одноэтажного каркаса состоит из колонн, защемленных в фундаментах, и опирающихся на них ригелей, состоящих из балок, ферм и других несущих конструкций. Соединение ригеля с колонной считается шарнирным. Жесткий диск покрытия здания и система связей обеспечивают совместную работу поперечных рам, поэтому крановая или другая горизонтальная нагрузка, приложенная к одной раме, будет воспринята и другими рамами, что следует учитывать в расчетах. Постоянную нагрузку от веса стропильных и подстропильных конструкций, а также панелей перекрытия, снега и подвесных кранов передают на колонны как вертикальные силы Next 3 и Next 2 (рис. 4.5, а). Вертикальные силы Next 3 от навесных стеновых панелей на крайние колонны принимают с эксцентриситетом e3 , составляющим полусумму толщины панели и высоты сечения колонны. Расстояние от силы Next1 до крайней координационной оси здания принимают 175 мм. Поэтому эксцентриситеты приложения этой силы в верхней части крайних колонн при нулевой их привязке составляют e2 0,5 h2 175 мм, а при привязке 250 мм будет e2 425 0,5 h2 (рис. 4.5,в). В подкрановой части колонны эксцентриситет приложения данной силы составляет e1 (h1 h2 ) / 2 . Таким образом, в сечениях колонн ниже перекрытия и выше подкрановой консоли действует изгибающие моменты соответственно M 2 Next1 e2 и M1 ( Next1 G2 ) e2 Next 3 e3 , где G2 - собственный вес верхней части колонны высотой H 2 . Для средних колонн учитывают возможность наличия различных давлений соседних ригелей, а также случайный эксцентриситет приложения силы Next 2 величиной 20 мм. Однако при расчете усилий рам данным эксцентриситетом пренебрегают. Временную ветровую нагрузку (положительное и отрицательное давление ветра), передающуюся на конструкции покрытия здания выше колонн, приводят к сосредоточенной горизонтальной силе W, приложенной в уровне верха рамы. Ветровые нагрузки на стеновые панели w1 и w2 являются распределенными по высоте крайних колонн. При этом учитываются нормативные рекомендации по учету изменения скоростного напора по высоте здания. Временную нагрузку от мостовых кранов определяют с учетом коэффициента надежности по нагрузке F 1,1 . Максимальное давление на одно колесо крана Fcr ,max имеет место, если его тележка с грузом находится вблизи подкрановой балки. Тогда на колеса крана с противоположной стороны действует давление Fcr ,min . Суммарное давление на четыре колеса крана составляет 2( Fcr ,max Fcr ,min ) G Gcr G1 , где G – вес груза, Gcr – собственный вес моста и G1 – вес тележки. Вертикальную нагрузку от мостовых кранов определяют с учетом положения колонны рамы. Нагрузка N cr на крайнюю колонну вычисляют от двух максимально сближенных кранов по линии влияния опорных реакций (рис. 4.5, д). При этом учитывается коэффициент сочетаний нагрузок 0,85. Нагрузку N cr на среднюю колонну определяют от четырех кранов с коэффициентом сочетаний 0,7. При этом учитывают максимальное давление крана на подкрановую балку с одного пролета рамы и минимальное с соседнего пролета. Расстояние от разбивочных осей подкрановых балок принято единым для всех схем зданий и составляет a=750 мм (рис. 4.5, г). В зданиях с мостовыми кранами грузоподъёмностью более 50 т, а также при наличии проходов в подкрановой части колонн данное расстояние увеличивается до 1000 мм. Допускается его принимать равным 500 мм в зданиях, оборудованных мостовыми электрическими кранами грузоподъемностью до 15 т и мостовыми ручными кранами любой грузоподъемности. Определение генеральных размеров поперечной рамы Компоновку поперечной рамы начинают с определения основных габаритных размеров элементов конструкций в плоскости рамы. Вертикальные габариты здания зависят от технологических условий производства и определяются расстоянием от уровня пола до головки кранового рельса H1 и расстоянием от головки кранового рельса до низа конструкций покрытия H2 Определение нагрузок на поперечную раму На здание может действовать одновременно несколько нагрузок и возможно несколько их сочетаний с учетом отсутствия некоторых из них или возможного изменения схем их приложения. Поэтому раму рассчитывают на каждую из нагрузок отдельно, а затем составляют наиболее невыгодные комбинации нагрузок по определенным правилам. Постоянные нагрузки от веса покрытия, собственной массы конструкций и стенового ограждения Постоянные нагрузки на ригель рамы от веса кровли, стропильных конструкций и связей по покрытию принимаются обычно равномерно распределенными по длине ригеля. Постоянные нагрузки зависят от типа покрытия, которое может быть тяжелым или легким, утепленным или не утепленным. Нагрузки от крановых воздействий Вертикальная крановая нагрузка передается на подкрановые балки в виде сосредоточенных сил Pmax и Pmin при их невыгодном положении на подкрановой балке. Нагрузки от давления ветра При расчете одноэтажных производственных зданий высотой до 36 м при отношении высоты к пролету менее 1,5, размещаемых в местностях типов А (открытая) и В (застроенная), учитывается только статическая составляющая ветровой нагрузки, соответствующая установившемуся напору на здание. Расчетное значение статической составляющей ветровой нагрузки в зависимости от высоты над поверхностью земли определяется по формуле: wm w0 k c F n , где w0 – нормативное значение ветрового давления, принимаемое в зависи- мости от района строительства. Согласно СНиП 2.01.07-85 [17…19] (карта 3 Приложения 5) г. Витебск расположен в 1-м ветровом районе, w0 0,23 23 кПа; k – коэффициент, учитывающий изменение ветрового давления в зависимости от высоты здания. Для местности типа В, при Н = 5 м; 10 м; 20 м и 40 м значения k соответственно равны 0,5; 0,65; 0,85; 1,1; / с – аэродинамический коэффициент; c 0,8 - для наветренной стороны, c 0,6 для подветренной стороны. 36. Последовательность статического расчета ПРЦ 1. Определение генеральных размеров поперечной рамы Компоновку поперечной рамы начинают с определения основных габаритных размеров элементов конструкций в плоскости рамы. Вертикальные габариты здания зависят от технологических условий производства и определяются расстоянием от уровня пола до головки кранового рельса H1 и расстоянием от головки кранового рельса до низа конструкций покрытия H2 2. Определение нагрузок на поперечную раму На здание может действовать одновременно несколько нагрузок и возможно несколько их сочетаний с учетом отсутствия некоторых из них или возможного изменения схем их приложения. Поэтому раму рассчитывают на каждую из нагрузок отдельно, а затем составляют наиболее невыгодные комбинации нагрузок по определенным правилам. 3. Постоянные нагрузки от веса покрытия, собственной массы конструкций и стенового ограждения Постоянные нагрузки на ригель рамы от веса кровли, стропильных конструкций и связей по покрытию принимаются обычно равномерно распределенными по длине ригеля. Постоянные нагрузки зависят от типа покрытия, которое может быть тяжелым или легким, утепленным или не утепленным. 4. Нагрузки от крановых воздействий Вертикальная крановая нагрузка передается на подкрановые балки в виде сосредоточенных сил Pmax и Pmin при их невыгодном положении на подкрановой балке. Вертикальная крановая нагрузка передается на подкрановые балки в виде сосредоточенных сил Pmax и Pmin при их невыгодном положении на подкрановой балке. Расчетное давление на колонну, к которой приближена тележка, определяется по формуле: Dmax=ψc⋅Pmax ⋅∑yi⋅γn⋅γF на противоположную колонну: Dmin=ψc⋅Pmin ⋅∑yi⋅γn⋅γF где ψc = 0,85– коэффициент сочетаний при совместной работе двух кранов в одном пролете для групп режимов работы кранов 1К…6К; γF =1,5– коэффициент безопасности по нагрузке для крановых нагрузок; Pmax – наибольшее вертикальное давление колес на подкрановую балку. Наименьшее давление колеса крана вычисляется по формуле: Pmin= – Pmax Q – грузоподъемность крана в т; G – полный вес крана с тележкой; n0 – число колес на одной стороне крана Горизонтальные нагрузки, возникающие при торможении крановой тележки, передаются на колонны через тормозные балки или фермы. Нормативную поперечную горизонтальную силу от торможения тележки Тk,0 определяют по формуле: Тk,0 = 0.05(Q⋅GT) GT – вес тележки Нормативная поперечная сила, действующая на одно колесо с одной стороны моста крана: Тk = где ntt – число тормозных колес тележки (для кранов с грузоподъемностью Q ≤ 30 т ntt = 2). Расчетное горизонтальное давление на колонну от двух сближенных кранов составляет: T= Тk ⋅∑yi⋅γn⋅γF Нагрузки от веса снегового покрова Расчетная снеговая нагрузка на крайнюю колонну определяется по формуле: Qs = s0⋅ µ⋅L/2⋅B⋅γn⋅γF где s0 – нормативное значение веса снегового покрова на 1 м2 горизонтальной поверхности земли, принимаемое в зависимости от района строительства. В снеговом районе 2Б нормативное значение снеговой нагрузки – s0 = 1,2 кПа; µ – коэффициент перехода от скатной кровли к горизонтальной поверхности. Для расчета рамы принимается µ = 1, так как α < 25°; γF = 1,5 – коэффициент безопасности по нагрузке для снега. Нагрузки от давления ветра При расчете одноэтажных производственных зданий высотой до 36 м при отношении высоты к пролету менее 1,5, размещаемых в местностях типов А (открытая) и В (застроенная), учитывается только статическая составляющая ветровой нагрузки, соответствующая установившемуся напору на здание. Расчетное значение статической составляющей ветровой нагрузки в зависимости от высоты над поверхностью земли определяется по формуле: wm w0 k c F n , где w0 – нормативное значение ветрового давления, принимаемое в зависи- мости от района строительства. Согласно СНиП 2.01.07-85 [17…19] (карта 3 Приложения 5) г. Витебск расположен в 1-м ветровом районе, w0 0,23 23 кПа; k – коэффициент, учитывающий изменение ветрового давления в зависимости от высоты здания. Для местности типа В, при Н = 5 м; 10 м; 20 м и 40 м значения k соответственно равны 0,5; 0,65; 0,85; 1,1; с – аэродинамический коэффициент; c 0,8 - для наветренной стороны, c/ 0,6 для подветренной стороны. Ординаты фактических эпюр расчетной погонной нагрузки на одну раму на высоте 5, 10, 20 м (при отметке верха парапета до 20 м) для активной и пассивной составляющих ветровой нагрузки определяются по формуле qw = w0⋅k⋅c⋅B⋅γn⋅γF, кН/м 37.Связи, применяемые в ОПЗ. Назначение. Пространственную жесткость каркаса, т.е. его способность сопротивляться воздействию горизонтальных нагрузок, обеспечивают защемленные в фундаментах колонны, жесткий диск покрытия и система стальных связей (вертикальных и горизонтальных). В поперечном направлении вертикальные связи не могут быть установлены, так как они препятствовали бы технологическому процессу. Поэтому пространственную жесткость каркаса в поперечном направлении обеспечивают колонны (по расчету) и диск покрытия, распределяющий местные горизонтальные нагрузки между колоннами. В продольном направлении общую устойчивость каркаса в целом обеспечивают вертикальные крестовые или портальные металлические связи по колоннам. В зданиях с мостовыми кранами такие связи устраиваются всегда и размещаются в одном шаге каждого ряда колонн посредине температурного блока на высоту от пола до низа подкрановых балок (рис.1.7, поз.6). Эти связи рассчитываются на действие ветровых нагрузок, приложенных к торцовым стенам, и продольных тормозных нагрузок от мостовых кранов. В бескрановых зданиях небольшой высоты (Н<9,6м) связи по колоннам могут не устанавливаться. При высоте опорных частей ригелей более 800мм, например в зданиях с плоской кровлей, между ними устанавливают вертикальные связи-фермы, располагаемые в крайних ячейках температурного блока, а поверху каждого продольного ряда колонн – стальные распорки (рис. 1.7.поз.4,5). Связи-фермы имеют номинальную длину 6 либо 12 м и высоту, равную высоте ригеля на опоре. В высоких зданиях (Н>18м) с большими пролетами, чтобы уменьшить горизонтальную силу на диск покрытия, устраивают дополнительные опоры у торцевых стен в уровне нижнего пояса стропильных балок или ферм в виде горизонтальных связей, служащих дополнительными опорами для колонн фахверка. Эти связи выполняются в виде горизонтальной фермы с крестовой решеткой из стальных уголоков, поясами которой служат нижние пояса двух смежных стропильных балок или ферм. Устойчивость сжатых поясов ригелей из плоскости при беспрогонной системе покрытия и отсутствии фонаря обеспечивается плитами покрытия, приваренными к ригелям с последующим замоноличиванием швов. Таким путем достигается образование жесткого диска, и необходимость постановки дополнительных связей в плоскости покрытия отпадает. Назначение связей: способствуют приданиюжесткости покрытия(при высоте балки на опоре h(оп) >900 мм – выполняются связи по стропильным конструкциям); обеспечивают устойчивость сжатых поясов, стоек ферм, опорных частей балок при высоте балки на опоре h(оп)>900 мм; без связи произойдет смещение верха стропильной конструкции; для восприятия ветровых нагрузок торцами здания; восприятние тормозных усилий вдоль здания от действия горизонтальных напряжений, вызванными мостовыми кранами. h(оп)<0,9м Вид здания h(оп)>0,9м Без крана, Н(к)<=10м Без крана, Н(к)>10м Крановое здание Разбивка зданий на температурные блоки. Основное назначение температурно-усадочных швов: для восприятия внутренних усилий к колоннах от внутренних перемещений в продольном и поперечном элементах вследствии переменной температуры наружного воздуха и усадки бетона. Максимальных температурный блок – 72 м(при температуре наружного воздуха до -40 ˚С для отапливаемых зданий); для неотапливаемых – 42 м. Поперечные температурно-усадочные швы выполняются на спаренных колоннах со смещением геометрической оси на 500 мм. При этом шов доводится до фундамента, колонны имеют общий фундамент. Иногда устраивается и продольные температурно-усадочные швы. 38. Расчет и конструирование ребристых плит покрытий. Плиты беспрогонных покрытий представляют собой крупные ребристые панели размером 2х12 и 3х6 м, которые опираются непосредственно на ригели поперечных рам; плиты 1,5х12 и 1,5х6 м используют как доборные элементы, в местах повышенных снеговых отложений у фонарей, в перепадах профиля покрытия. Плиты другого типа – прогонных покрытий значительно меньших размеров (3х0,5 и 1,5х0,5 м) – опираются на железобетонные прогоны, которые, в свою очередь, опираются на ригели поперечных рам. Беспрогонная система покрытия в наибольшей степени отвечает требованиям укрупнения элементов, уменьшения числа монтажных единиц и является основной в строительстве ОПЗ. Ребристые плиты 3х12 м, принятые в качестве типовых, имеют продольные ребра сечением 100х450 мм, поперечные ребра 40х150 мм, полку толщиной 25 мм, уширения в углах – вуты, которыми обеспечивается надежность работы в условиях систематического воздействия горизонтальных усилий от торможения мостового крана. Продольные ребра армируются напрягаемой арматурой, поперечные ребра и полки – сварными каркасами и сетками. Бетон принимают классов В30, В40(теперь уже С). Плиты ребристые 3х6 м, также приняты в качестве типовых, имеют продольные и поперечные ребра и армируются напрягаемой арматурой. Плиты двухконсольные 2Т размерами 3х12 и 3х6 м имеют продольные ребра, расположенные на расстоянии 1,5 м и консольные свесы полок. Благодаря уменьшению изгибающих моментов в поперечном направлении ребер не делают, форма плиты упрощается. В плитах размером 3х12 м продольные предварительно напряженные ребра изготовляют заранее, а затем бетонируют полку. Связь ребер с полкой создается устройством выпусков арматуры и сцеплением бетона. Раздельное изготовление плиты позволяет снизить класс бетона полок до С15. Плиты 3х6 и изготовляют как раздельно, так и целиком. Технические решения крупноразмерных плит 3х18 и 3х24 м, опирающихся на балки пролетом 6 или 12 м, разработаны для покрытий со скатной и малоуклонной кровлей. Плиты 2Т в этом решении имеют трапецеевидные продольные ребра с уклоном верхнего пояса 1:12 и полку переменной толщины (25-60 мм). Плиты крупноразмерные ж/б сводчатые. УЖС имеют криволинейные продольные ребра с уширениями в нижней и верхней частях, гладкую полку толщиной 40-50 мм в середине пролета, 140-160 мм в торце у опор. Плиты ребристые под малоуклонную кровлю имеют трапецеевидные продольные ребра ребра с уклоном верхнего пояса 1:20, 1:30, поперечные ребра с шагом 1000 мм и полку толщиной 25 мм. Высота панелей перекрытия определяется главными требованиями жесткости. Предварительно высоту панели можно определить по формуле: h cl0 , где с – коэф. для ребристых плит с полкой в сжатой зоне – 30 – 34; Высоту предварительно напряженных плит можно определить: h l0 / 20 При расчете прочности по изгибающему моменту ширина ребра принимается равной сумме ширине всех ребер плиты, а расчетная ширина сжатой полки принимается равной полной ширине панели. Расчет прочности плит сводится к расчету таврового сечения с полкой в сжатой зоне. В большинстве случаев н.о. проходит в пределах толщины сжатой полки, поэтом, определив: A0 M / fcd b f ' h02 Находят по таблице и , проверяют условие x h0 h f Затем находят площадь растянутой арматуры As M / fcd h0 Для случаев, когда x h h f и н.о. пересекает ребро, расчет ведут с учетом сжатия в ребре. Расчетную ширину сечения плиты с ребрами вверх принимают равной суммарной ширине ребер и расчет ведут как для прямоугольного сечения. Поперечную арматуру плиты из условия прочности по наклонному сечению, рассчитывают по расчетной ширине ребра b, равной суммарной ширине всех ребер сечения. Полка панели работает на местный изгиб как частично защемленная на опорах плита пролетом l0 , равным расстоянию в свету между ребрами. В ребристых панелях с ребрами вниз защемление полки создается заливкой бетоном швов, препятствующей повороту ребра. Изгибающий момент - M ql02 / 11.В ребристых панели с поперечными промежуточными ребрами изгибающие моменты полки могут определяется как в плите, опертой по контуру и работающей в двух направлениях. 39. Стропильные балки покрытий ОПЗ. Виды. Расчет и конструирование. Железобетонные стропильные балки применяют для перекрытия пролетов 6, 9, 12 и 18 м. При пролетах 24 м и более они уступают фермам по технико-экономическим показателям и, как правило, не используются. Балки пролетами 6 и 9 м предназначены преимущественно для покрытия пристроек, а балки пролетом 12 м — в качестве поперечных или продольных ригелей покрытия. Балки пролетом 18 м применяют в качестве поперечных ригелей, по которым укладывают плиты 3x6 или 3х12 м. В зависимости от профиля кровли балки бывают двускатными, односкатными, с параллельными полками, с ломаным или криволинейным очертанием верхней полки. Двускатные балки имеют уклон верхней полки 1:12 для скатных кровель, 1:30 — для малоуклонных кровель. Из-за экономичности их чаще других применяют для покрытий пролетов 18 м. Определенные трудности при их изготовлении связаны с устройством каркасов переменной высоты. При необходимости пропуска коммуникаций в уровне покрытия (воздуховоды и т.п.) используют двускатные решетчатые балки пролетом 12 и 18 м. Односкатные балки обычно применяют для устройства кровли с односторонним уклоном, например, в пристройках. Балки с криволинейным верхним поясом приближены по форме к эпюре моментов, они выгоднее по расходу материала но труднее в изготовлении. Балки с параллельными полками наиболее просты в изготовлении, имеют арматурные каркасы постоянной высоты и применяются в качестве продольных ригелей при горизонтальных кровлях. Однако по расходу бетона и арматуры они уступают двускатным. Балки с ломаным и криволинейным верхним поясом, несмотря на экономичность, не нашли широкого применения из-за сложности их изготовления. Высота сечения балок в середине пролета (1/10…1/12 )L. В целях экономии бетона сечение балок принимают тавровым (при L = 6; 9 м) и двутавровым ( L=12; 18 м). Ширину верхней полки балок, из условия опирания плит покрытия и обеспечения устойчивости при транспортировании и монтаже, принимают равной 1/50...1/60, что обычно составляет 20...40 см. Ширину нижней полки (25...30 см) определяют из условия размещения в ней растянутой арматуры, прочности бетонного пояса при действии усилия обжатия, а также способа опирания балки на колонны. Толщину вертикальной стенки в средней части пролета (6...8 см) назначают исходя из условий изготовления балки (в вертикальном положении) и размещения поперечной арматуры (одного или двух каркасов). У опор стенка утолщается, что обеспечивает прочность и трещиностойкость опорных сечений. Балки покрытий изготавливают из тяжелого бетона классов В25...В50 и из бетона на пористых заполнителях классов В25...В40. В основном применяют предварительно напряженные конструкции, армируемые высокопрочными стержнями, одиночной высокопрочной проволокой или пучками из нее, используются и семипроволочные канаты. Балки изготавливают на заводах строительных материалов и конструкций с натяжением арматуры на упоры. Типовые балки со сплошным двутавровым поперечным сечением и решетчатые разработаны с несколькими вариантами армирования продольной напрягаемой арматурой классов А-IV, А-iv, А-iv, Вр-П и К-7. Балки рассчитывают на равномерно распределенные нагрузки от собственного веса, веса кровли и снега, а также на сосредоточенные силы от веса фонаря и подвесного транспорта, если он есть в здании, при этом учитывается наиболее невыгодное сочетание нагрузок. Расчет выполняется по первой и второй группам предельных состояний на прочность, по образованию и раскрытию трещин и по деформациям. Значения расчетных изгибающих моментов и поперечных сил, а также величину прогиба находят из расчета шарнирно опертой однопролетной балки. Считается целесообразным уменьшить количество продольной не напрягаемой арматуры в соответствии с построенной эпюрой материалов. Расчет прочности по нормальным сечениям ведется по правилам проектирования изгибаемых элементов двутаврового поперечного сечения (как в изгибаемых элементах). Следует иметь в виду, что в двускатных балках наиболее опасным оказывается нормальное сечение, расположенное не в середине пролета, а на расстоянии (0,3…0,4L) от опоры. Требуемая площадь поперечной арматуры назначается в результате расчета прочности балки по наклонным сечениям. Опорные зоны балок дополнительно рассчитываются на местное действие опорной реакции и усилия предварительного обжатия. Прочность и трещиностойкость балок также проверяется во время складирования, транспортировки и монтажа. В последнее время в практике строительства стали применять более экономичные конструкции покрытий, проектируемые по беспрогонной схеме, и постоянно разрабатываются новые конструктивные решения. Особенности расчета и конструирования двускатных железобетонных стропильных балок (определение наиболее нагруженного сечения, расчет и конструирование опорного и конькового узлов). 1) Назначение размеров. l0 L Где L – разбивочная длина; 40..60 Расчётный пролёт принимается равным расстоянию между серединами закладных деталей. l расч L разбив 300 hоп 800 . Для двускатной hоп 800; 900; 1000. 2) Расчётное сечение для балки: Наиболее опасное сечение расположено на расстоянии 0.37 расчётного пролёта: Ширина верхнего пояса обычно принимается от 240 до 400 мм. Бетон от С25/30 до С50/60. Обычно С25/30, C30/37, C45/50. 3) Сбор нагрузки: - собственный вес (на 20% больше) - снег 4) Подбор арматуры. Расчёт следует выполнять по эквивалентному сечению. Предварительный подбор площади сечения напрягаемой арматуры выполняем по методу предельных усилий. Продольную ненапрягаемую арматуру, установленную в верхней полке не учитываем. Если момент больше, чем расчётный, то увеличиваем класс бетона. Диаметры продольной арматуры: 18, 20… Нежелательно чтобы они были разными. Стержни ставить симметрично относительно вертикальной оси. Кол-во рядов как правило 3. По ширине обычно 3-5. Опорный узел: lpt – базовая длина зоны передачи напряжений Зададимся шагом поперечной арматуры. Определяем предварительную площадь поперечной арматуры. Определяем поперечные усилия, воспринимаемые бетоном и поперечной арматурой. Проверяем VRD>VSD, ρSW<ρSW,min. Окончательно принимаем поперечную арматуру. Устанавливается чтобы не было трещин между сжатой и растянутой зоной. Арматура в коньковом узле устанавливается по конструктивным соображениям. Прочность балки в коньке на отрыв верхней полки от стенки обеспечивается стержнями П-образной формы. 40. Стропильные фермы покрытий ОПЗ. Виды. Расчет и конструирование. Железобетонные фермы применяют в качестве ригелей покрытий при пролетах 18 м и более и шаге 6 или 12 м. Наиболее рационально применять их при пролетах 24 и 30 м. При пролете 18 м экономичнее балки покрытий, но часто применяют и фермы, особенно при наличии разнообразных технологических коммуникаций (воздуховодов, трубопроводов, кабелей и т.п.), которые удобно разместить в межферменном пространстве. Фермы с пролетами более 30 м получаются слишком тяжелыми, требуется членение их на отдельные блоки с последующей укрупнительной сборкой, что существенно увеличивает стоимость. Очертание поясов и решетки железобетонных ферм зависит от профиля кровли и общей компоновки покрытия (скатного, малоуклонного, плоского). Рисунок 95.1 — Типы железобетонных ферм: а — сегментные с верхним поясом ломаного очертания и раскосной решеткой; б — арочные раскосные с редкой решеткой и верхним поясом криволинейного очертания; в — арочные безраскосные с жесткими узлами (стропильные рамы); г,д — полигональные с параллельными поясами или трапециевидного очертания с малым уклоном верхнего пояса и раскосной решеткой. Наиболее рациональное по статической работе очертание верхнего пояса — сегментное или арочное, приближающееся к кривой давления. У таких ферм усилия в поясах по длине пролета изменяются незначительно, а усилия в элементах решетки невелики. Кроме того, в таких фермах высота на опоре небольшая, что снижает массу фермы и высоту наружных стен. Высоту всех типов ферм принимают равной 1/7...1/9 пролета. Панели верхнего пояса всех типов ферм, за исключением арочных раскосных, проектируют размером 3 м, что обеспечивает передачу нагрузки от плит покрытия в узлы ферм и исключает местный изгиб верхнего пояса. В арочных раскосных фермах расстояния между узлами верхнего пояса достигает 4,5...6 м, в связи с чем возникает местный изгиб. Однако изгибающие моменты Мр от внеузловой вертикальной нагрузки частично компенсируются моментами М обратного знака, возникающими вследствие эксцентриситета продольных сил в верхнем поясе. Такие фермы экономичнее сегментных при пролетах 30 м и более. Решетка ферм может быть закладной, изготовляемой заранее, или чаще цельной, бетонируемой одновременно с поясами. В последнем случае ширина сечения элементов решетки принимается равной ширине поясов. Фермы готовят из высокопрочных бетонов классов B30...B60 с большим содержанием арматуры в поясах. Это позволяет уменьшить размеры сечения элементов и снизить массу фермы. Нижний пояс выполняется предварительно напряженным и армируется стержневой арматурой, высокопрочной проволокой, арматурными канатами К7 или К19 с натяжением на упоры стенда. Чтобы предотвратить появление продольных трещин, которые могут возникнуть по технологическим причинам, напрягаемая арматура окаймляется легкими каркасами из проволоки диаметром 5...6 мм. Длина каркасов принимается не более 2...3 м, чтобы они не препятствовали равномерному обжатию нижнего пояса. Верхний пояс и элементы решетки армируются сварными каркасами из арматуры. Особое внимание уделяется армированию опорных и промежуточных узлов. В опорных узлах устанавливают по расчету по два плоских каркаса с поперечной рабочей арматурой, обеспечивающей прочность по наклонным сечениям, а также дополнительную продольную ненапрягаемую арматуру и сетки косвенного армирования, что обеспечивает надежность анкеровки напрягаемой арматуры. Промежуточные узлы верхнего и нижнего поясов армируют сварными каркасами, состоящими из поперечных стержней диаметром 6-10 мм с шагом 100 мм и окаймляющего цельногнутого стержня диаметром 10...18. Арматуру элементов решетки заводят в узлы с уширениями (вутами), растянутые стержни надежно анкеруют. В узлах железобетонных ферм для надежной передачи усилий от одного элемента к другому создают специальные уширения — вуты, позволяющие лучше разместить и заанкерить арматуру решетки. Узлы армируют окаймляющими цельногнутыми стержнями диаметром 10-18 мм и вертикальными поперечными стержнями диаметром 5-10 мм с шагом 100-200 мм, объединенными в сварные каркасы. Расчет ферм выполняют на действие постоянных (вес покрытия, фермы, фонарей) и временных (снег, подвесной транспорт и т.д.) нагрузок. Нагрузку от покрытия и веса фермы приводят к узловой и прикладывают в узлы верхнего пояса, нагрузку от подвесного транспорта — в узлы верхнего иди нижнего пояса в зависимости от конструкции крепления крановых путей. Учитывается возможное неравномерное загружение фермы снегом около фонарей, в местах перепада высот и по покрытию многопролетных зданий; рассматривают также загружение снегом и подвесным транспортом одной половины фермы, невыгодное для элементов решетки. Расчетную схему фермы с раскосной решеткой допускается принимать в виде стержневой системы с шарнирными узлами, т.е. без учета жесткости узлов. Тогда при действии узловой нагрузки все элементы такой системы испытывают только осевые усилия (сжатие или растяжение). Статический расчет этой системы (определение усилий в ее элементах) можно выполнять любым способом: построением диаграммы Максвелла-Кремоны, вырезанием узлов способом сечений. При наличии внеузловой нагрузки необходимо учитывать изгибающие моменты от местного изгиба, для определения которых верхний пояс рассматривается как многопролетная неразрезная балка с ломаной осью. Расчетная схема безраскосной фермы представляет многократно статически неопределимую замкнутую раму с жесткими узлами, статический расчет которой производится на ЭВМ. Верхний сжатый пояс и решетки армируют ненапрягаемой арматурой в виде сварных каркасов. Нижний растянутый пояс, а также элементы решетки (при значительных в них усилиях) выполняют преднапряженными. Опорные узлы фермы армируют дополнительной продольной ненапрягаемой арматурой и поперечными стержнями, обеспечивающими надежность анкеровки растянутой арматуры нижнего пояса и прочность опорного узла по наклонному сечению. Подстропильные фермы Подстропильные фермы применяют в средних рядах многопролетных зданий для опирания стропильных балок или ферм в тех случаях, когда их шаг составляет 6 м, а шаг колонн средних рядов 12 м. Длина подстропильных ферм равна 12 м, однако в дальнейшем предполагается применение этих конструкций длиной 18 и 24 м. Рисунок 95.1 — Подстропильная ферма Подстропильные фермы используют в покрытиях со стропильными фермами. Подстропильные конструкции устанавливают вдоль здания по верху колонн и скрепляют с ними сваркой закладных деталей. Для опирания стропильных конструкций по концам и по середине подстропильных ферм предусмотрены закладные листы с приваренными к ним анкерными болтами. Стропильные конструкции соединяют с подстропильными анкерными болтами и сваркой. В зданиях с подстропильными конструкциями с целью сохранения унифицированной высоты помещений применяют колонны, укороченные на 700 мм, т.е. на высоту опорной части подстропильных конструкций. Подстропильные конструкции выполняют преднапряженными из бетона классов В30...В40 и армируют канатами, стержневой или проволочной арматурой с натяжением на упоры. Ненапрягаемую арматуру растянутых раскосов подстропильных ферм определяют из расчета прочности и раскрытия трещин. Крепление стропильных ферм к подстропильным конструкциям выполняют монтажной сваркой. Нагрузка от стропильной фермы передается в виде сосредоточенной силы, приложенной в середине пролета к нижнему узлу подстропильной фермы. Подстропильные фермы рассчитывают по прочности и трещиностойкости с учетом жесткости узлов. РАСЧЁТ УЗЛОВ 1.опорный узел Доп. арматура нижнего пояса: Ast (доп ) 0,2 Asp f pd fyd (доп арматура вопринимает 20% усилия) Условие равновесия: Ft Fpt Fst Vsw ctg Vsw s sw 50..150 мм; σ sd f yd Ft Fpt Fst ctg ; Vsw v sw ; v sw an ; σ pd f pd an ;для предварит. напряженной ар ры. bd bpd . Fst ( pt) σ sd(pd) Asd ( pd ) Сумма моментов относительно точки 0. M sd R(lsup , a); M Rd Fst z Fpt z Vsw c / 2; M sd M Rd 2 Промежуточный узел Vsw cos Ft ( an 2 a) / bd As fywd Asw a доп. длина анкеровки за счёт приварки коротышей Ns ; n 2(обычно) Ns 0,04(Ft max 0,5Ft min ) n fyd ssw 41. Арки покрытий ОПЗ. Расчет и конструирование. Рис.1. Железобетонная арка двутаврового сечении с затяжкой Классификация: -трехшарнирные -двухшарнирные -безшарнирные Арками называются рамы, состоящие из криволинейных элементов, горизонтальное смещение опор которых ограничено. Ограничение смещения приводит к возникновению распора в арках и арки работают преимущественно на сжатие. В трехшарнирных арках смещение опор в вертикальном и горизонтальном направлениях практически не сказывается на усилиях. В двухшарнирных арках усилия малочувствительны к вертикальным осадкам и более чувствительны к горизонтальным смещениям. В бесшарнирных арках любое смещение опор вызывает дополнительные значительные усилия и их принимают в тех случаях, когда смещение опор небольшое. Распор воспринимается затяжкой. Если устройство затяжки невозможно или нежелательно, то распор передают на жесткие боковые рамы (контфорсы) или фундаменты. 1- криволинейный элемент 2- шарнир 3- фундамент 4- затяжка 5- рама (контрфорс) При пролете свыше 30 м железобетонные арки становятся экономичнее ферм. Наиболее распространенные арки - двухшарнирные - выполняют пологими со стрелой подъема f=(1/6..l/8)l. В конструктивном отношении выгодно очертание оси арки, близкое к кривой давления. Распор арки передают на фундаменты и грунты основания. При слабых грунтах для восприятия распора арки устраивают затяжку, расположенную ниже уровня пола. Арки рассчитывают на вес покрытия и арки, сплошную и одностороннюю нагрузку от снега и сосредоточенную нагрузку от подвесного транспорта. Большепролетные арки рассчитывают также на усадку и ползучесть бетона, а высокие арки - на ветровую нагрузку. В расчетной схеме очертание пологой двухшарнирной арки принимают по квадратной параболе (рис.2,а), Высоту и ширину сечения арки предварительно принимают h=(1/30…1/40)l; b=(0,4…0,5)h. (4) Площадь сечения арматуры затяжки предварительно подбирают по распору Затяжки обычно устраиваются преднапряженные, так как они работают на растяжение Если арка цельная то это как правило 2-шарнирная Двухшарнирные арки рассчитывают как статически неопределимые системы с учетом влияния перемещений от изгибающих моментов и нормальных сил. Расчет с помощью методов строит. Механики и программными комплексами. Для преднапряженных затяжек в расчете учитываюу приведенную площадь бетона. Предварительное напряжение затяжки, в результате которого деформаций арматуры оказываются выбранными, уменьшает подвижность опор арки и приближает её работу под нагрузкой к работе арок с неподвижными пятами. При этом распор H увеличивается, а изгибающий момент арки уменьшается. Если арка состоит из 3 полуарок , то она относится к 3-шарнирным .Трехшарнирные арки статически не определимы. Если опоры расположены в M одном уровне, то распор арка статически поределима : H bx , M bx балочный f момент в середине пролета арки. Усилия M, Q, N определяют определяют в нескольких сечениях по длине арки (рис. 2,б). В практике проектирования, величину распора арки с постоянным сечением по длине, очертанию по дуге окружности или квадратной параболе определяют следующим образом: k q l2 H 8 f M ax M bx M yax N ax H cos Vbx cos Vax Vbx cos H sin k коэффициент учитывающий упругую податливость здания(принимается 0,9) По найденным значениям распора в сечениях арки и находится M ax , Nax ,Vax , Nbx ,Vbx усилие в том же сечении при расчете простой балки. угол между касательной к оси арки в рассматриваемом сечении к оси горизонта. Усилия в сечениях арки, вычисленные от разных загружений, сводят в таблицу и определяют наиболее невыгодное сочетание нагрузок: - от покрытия - собственный вес -снеговая а всем пролете -снеговая, на половине пролета арки. - сосредоточенная от подвесного транспортного оборудования Подбор размеров осуществляется как для внецентренно сжатого элемента. Для учета влияния продольного изгиба в плоскости кривизны расчетную длину принимают: -для 3хшарнирной арки - 0,58 l -двухшарнирной арки- 0,54 l -бесшарнирной арки- 0,36 l L- длина арки. Затяжку арки рассчитывают на центральное растяжение пренебрегая изгибным моментом от собственной массы затяжки. Арматуру определяют по условию прочности и затем проверяют трещиностойкость. Конструирование арок Выполняется согласно общим требованиям для внецентренно сжатых элементов. Поперечное сечение может быть прямоугольное и двутавровое. Армирование выполняется поперечное двойное, так как в сечении возможны знакопеременный момент. Для уменьшения провисания затяжки через каждые 5-6 м устраивают подвески. Большепролетные высокие арки имеют более сложное очертание оси и поэтому они чаще выполняются 3хшарнирными. 42. Крупноразмерные плиты покрытий 2Т. Плиты беспрогонных покрытий представляют собой крупные ребристые панели размером 3×12 и 3×6 м, которые опираются непосредственно на ригели поперечных рам; плиты 1,5×12 и 1,5×6 м используют как доборные элементы, в местах повышенных снеговых отложений у фонарей, в перепадах профиля покрытия. Плиты другого типа - прогонных покрытий значительно меньших размеров (3×0.5 и 1,5×0,5 м) - опираются на железобетонные прогоны, которые, в свою очередь, опираются на ригели поперечных рам. Беспрогонная система покрытий в наибольшей степени отвечает требованиям укрупнения элементов, уменьшения числа монтажных единиц и является основной в строительстве одноэтажных каркасных зданий. а) – с прогонами вдоль здания; б) – с крупноразмерными панелями; 1 – плиты; 2 – прогоны; 3 – ригели; 4 – крупнопанельные плиты Рис. 14.1. Схема покрытий Железобетонные плиты покрытия подразделяют на П-образные, типа 2-Т и крупноразмерные. Как правило, применяют плиты шириной 3 м, а шириной 1,5 м используют как доборные в местах повышенных снеговых отложений — у фонарей, в перепадах профиля покрытия — а также как более надежные для покрытий зданий с сильно агрессивной средой. Двухконсольные панели типа 2Т размерами 3x12, 3x18 м и 3x24 м имеют продольные ребра, расположенные па расстоянии 1,5 м, и консольные свесы полок (рис. 5.1, б). Плиты пролетом 18 и 24 м , опирающихся на балки пролетом 6м и 12м для скатной и малоуклонной кровли выполняют с ребрами трапециевидного профиля с уклоном верхнего пояса 1:12 и полкой переменной толщины (25... 60 мм). Вследствие наличия консолей изгибающие моменты в полке значительно снижаются, поэтому поперечные ребра в таких плитах не делают. Благодаря уменьшению изгибающих моментов в поперечном направлении ребер не делают, упрощается опалубка и изготовление плит, обеспечивается более равномерное обжатие продольных ребер по длине плиты. К недостаткам этих конструкций относится сложность устройства продольных швов между плитами из-за разных выгибов смежных плит. В плитах 3х12м продольное предварительно напр. Ребра изготавливают заранее, а затем бетонируют полку. Связь ребра создается устройством выпусков арматуры и сцеплением бетона. Раздельное изготовление позволяет снизить класс бетона до С10/15. Плиты 3х6 изг-т как раздельно так и целиком. Продольные предварительно напряженные ребра целесообразно готовить заранее на бетона классов В25... В40, а затем бетонировать полку из бетона классов В12,5-В15. Связь ребер с полкой обеспечивается устройством выпусков поперечной арматуры и сцеплением бетона. В приопорных верхних зонах ребер целесообразно создавать пазы для: образования шпонок после бетонирования полки. Продольная арматура ребер — из высокопрочной стали, полка армируется сетками из проволоки Вр-1. В продольном направлении плиты рассчитывают как свободно опертые однопролетные балки таврового сечения, в поперечном — как двухконсольную однопролетную плиту прямоугольного сеченая. а – монолитная ребристая панель с проволочной арматурой; б – сборномонолитная ребристая панель с предварительно изготовленными ребрами; в – армирование продольных ребер предварительно напрягаемыми стержнями (1), высокопрочной проволокой (2) и канатами (3) 43.Крупноразмерные плиты покрытий под малоуклонные кровли. Плиты беспрогонных покрытий представляют собой крупные ребристые панели размером 2х12 и 3х6 м, которые опираются непосредственно на ригели поперечных рам; плиты 1,5х12 и 1,5х6 м используют как доборные элементы, в местах повышенных снеговых отложений у фонарей, в перепадах профиля покрытия. Плиты другого типа – прогонных покрытий значительно меньших размеров (3х0,5 и 1,5х0,5 м) – опираются на железобетонные прогоны, которые, в свою очередь, опираются на ригели поперечных рам. Беспрогонная система покрытия в наибольшей степени отвечает требованиям укрупнения элементов, уменьшения числа монтажных единиц и является основной в строительстве ОПЗ. Ребристые плиты 3х12 м, принятые в качестве типовых, имеют продольные ребра сечением 100х450 мм, поперечные ребра 40х150 мм, полку толщиной 25 мм, уширения в углах – вуты, которыми обеспечивается надежность работы в условиях систематического воздействия горизонтальных усилий от торможения мостового крана. Продольные ребра армируются напрягаемой арматурой, поперечные ребра и полки – сварными каркасами и сетками. Бетон принимают классов В30, В40(теперь уже С). Плиты ребристые 3х6 м, также приняты в качестве типовых, имеют продольные и поперечные ребра и армируются напрягаемой арматурой. Рис. 9.1 – Ребристая плита покрытия Плиты двухконсольные 2Т размерами 3х12 и 3х6 м имеют продольные ребра, расположенные на расстоянии 1,5 м и консольные свесы полок. Благодаря уменьшению изгибающих моментов в поперечном направлении ребер не делают, форма плиты упрощается. В плитах размером 3х12 м продольные предварительно напряженные ребра изготовляют заранее, а затем бетонируют полку. Связь ребер с полкой создается устройством выпусков арматуры и сцеплением бетона. Раздельное изготовление плиты позволяет снизить класс бетона полок до С15. Плиты 3х6 и изготовляют как раздельно, так и целиком. Технические решения крупноразмерных плит 3х18 и 3х24 м, опирающихся на балки пролетом 6 или 12 м, разработаны для покрытий со скатной и малоуклонной кровлей. Плиты 2Т в этом решении имеют трапецеевидные продольные ребра с уклоном верхнего пояса 1:12 и полку переменной толщины (25-60 мм). Плиты крупноразмерные ж/б сводчатые. УЖС имеют криволинейные продольные ребра с уширениями в нижней и верхней частях, гладкую полку толщиной 40-50 мм в середине пролета, 140-160 мм в торце у опор. Плиты ребристые под малоуклонную кровлю имеют трапецеевидные продольные ребра ребра с уклоном верхнего пояса 1:20, 1:30, поперечные ребра с шагом 1000 мм и полку толщиной 25 мм. Высота панелей перекрытия определяется главными требованиями жесткости. Предварительно высоту панели можно определить по формуле: h cl0 , где с – коэф. для ребристых плит с полкой в сжатой зоне – 30 – 34; Высоту предварительно напряженных плит можно определить: h l0 / 20 При расчете прочности по изгибающему моменту ширина ребра принимается равной сумме ширине всех ребер плиты, а расчетная ширина сжатой полки принимается равной полной ширине панели. Расчет прочности плит сводится к расчету таврового сечения с полкой в сжатой зоне. В большинстве случаев н.о. проходит в пределах толщины сжатой полки, поэтом, определив: A0 M / fcd b f ' h02 Находят по таблице и , проверяют условие x h0 h f Затем находят площадь растянутой арматуры As M / fcd h0 Для случаев, когда x h h f и н.о. пересекает ребро, расчет ведут с учетом сжатия в ребре. Расчетную ширину сечения плиты с ребрами вверх принимают равной суммарной ширине ребер и расчет ведут как для прямоугольного сечения. Поперечную арматуру плиты из условия прочности по наклонному сечению, рассчитывают по расчетной ширине ребра b, равной суммарной ширине всех ребер сечения. Полка панели работает на местный изгиб как частично защемленная на опорах плита пролетом l0 , равным расстоянию в свету между ребрами. В ребристых панелях с ребрами вниз защемление полки создается заливкой бетоном швов, препятствующей повороту ребра. Изгибающий момент M ql02 / 11 В ребристых панели с поперечными промежуточными ребрами изгибающие моменты полки могут определяется как в плите, опертой по контуру и работающей в двух направлениях. По технико-экономическим показателям ребристые малоуклонные плиты немного уступают сводчатым плитам КЖС, однако их преимущество в том, что при малом уклоне покрытия можно широко применять средства механизации в производстве кровельных работ. При криволинейной поверхности сводчатых плит это затруднено 44.Крупноразмерные железобетонные сводчатые панели КЖС. КЖС представляет собой короткую цилиндрическую оболочку с предварительно напряженными ребрами — диафрагмами сегментного очертания . Размеры плит в плане 3x12, 3x18 и 3X24 м. Очертание поверхности оболочки принимают по квадратной параболе Толщина оболочки не должна быть менее 30 мм в середине пролета с утолщением до 140...160 мм у торцов Высоту поперечного сечения плиты в середине пролёта принимают (1/15...1/20) в зависимости от пролета и нагрузки. Для уменьшения массы плиты диафрагмы проектируют минимальной толщины (40 мм) с вертикальными ребрами жесткости. Основную напрягаемую арматуру располагают в нижней части диафрагмы. По концам напрягаемых стержней предусматривают анкерные детали, обеспечивающие падежное закрепление рабочей арматуры в бетоне опорного узла. Эта арматура играет роль затяжки рассматриваемой сводчатой системы. Диафрагму армируют сварными каркасами только в опорных зонах, в вертикальных ребрах устанавливаю: стержни-подвески. Армируют оболочки сварной сеткой, подбираемой по расчету. Сопряжение оболочки с диафрагмой выполняют с помощью пологих вутов. Плиты КЖС проектируют из бетоннов классов В25, В50 в зависимости от пролетов и нагрузок. При расчете плиту рассматривают как цилиндрический свод, работающий совместно с диафрагмами. Полагают, что вдоль направляющей оболочки действует только продольная сила N. поперек — поперечные силы С и изгибающие моменты М . Изгибающий момент в системе «оболочка — диафрагма» (в продольном направлении) воспринимается растянутой арматурой диафрагмы и полкой (оболочкой), работающей на сжатие. Плиты КЖС экономичны, достаточно просты в изготовлении. Наиболее существенный их недостаток — трудоемкость устройства кровли по криволинейной поверхности. Плиты крупноразмерные железобетонные сводчатые КЖС имеют криволинейные продольные ребра с уширениями в нижней и верхней частях, гладкую полку толщиной 40…50 мм в середине пролета, 140…160 мм в торце у опор. Рис. 14.6. Конструкция сводчатой крупноразмерной панели КЖ 45. Расчет и конструирование колонн сплошного сечения ОПЗ. Типы поперечных сечений: сплошные, двухветвевые. По назначению: без мостовых кранов, с мостовыми кранами, с подвесными кранами. Сплошные: -прямоугольные, круглые, кольцевые, двутавровые, х-образные, побразные. Сечение колонны: кр. колонна: 300х300,300х400,400х400,400х500. средняя колонна: 300х300,300х400,400х400,400х500,500х600. Габариты по высоте: 3; 3,6; 4,2; 4,8; 5,4; 6; 7,2; 8,4; 9,6; безкрановые. 10,8; 12; 13,2; 14,4; 15,6; 16,8; 18, крановые. До 14,4 м возможно применять сплошные колонны, больше – двухветвевые. Армирование: для армирования применяют продольную арматуру S400,S500. Поперечная арматура: S400,S500. Применение предварительного напряжения: для уменьшения гибкости (увелич. устойчивости), в других случаях смысла нет. S800, S1200(стержневая). Расчет колонн: 1) Определяем расчетные сочетания нагрузок. 2) Определяем гибкость элемента: ; 3)Определение необходимости учета продольного изгиба: 4)Определение N crit 6,4 Ecm I c 0,11 [ ( ) eIs ] 2 k lt l0 0,1 e p 5) Определение <=2.5 – коэф. увеличения момента; 6)Определение расчетных моментов в сечении: M1 – изгибающий момент у рассматриваемого конца элемента. – где – макс. момент в средн. трети сечения. 7)Определение расчетных эксцентриситетов; 8)Определение момента с учетом продольного изгиба; 9) Подбор площади симметричного армирования; Таким образом отдельно рассчитывается надкрановая и подкрановая ветви. 10)Конструирование. 11)Расчет консоли. При вылете 100-150 мм консоль может не иметь вута и конструироваться прямоугольной. При вылете более 150 мм консоль должна иметь вут с углом наклона величиной 45 о.Ширина консоли должна быть равной ширине колонны. Исключение могут составлять консоли, устраиваемые в широких подколонниках для опирания фундаментных балок. Высота консоли и ее арматура назначаются по расчету. Консоли армируются поперечной и продольной арматурой. Поперечная арматура коротких консолей при сварных и вязаных каркасах колонн конструируется следующим образом: — при h 2,5 a - в виде наклонных хомутов по всей высоте консоли; — при h 2,5 a - в виде отогнутых стержней и горизонтальных хомутов по всей высоте консоли; — при h 3,5 a и Q Rp b h0 - в виде горизонтальных хомутов без отогнутых стержней, которые в этом случае допускается не предусматривать; здесь ho принимается в опорном сечении консолей.Во всех случаях шаг хомутов должен быть не более h/4 и не более 150 мм; диаметр отогнутых стержней должен быть не более 1/15 длины отгиба loтг и не более 25 мм. При этом суммарная площадь сечения наклонных хомутов и отогнутых стержней, пересекающих верхнюю половину линии длиной l, соединяющей точки приложения силы Q и сопряжения нижней грани консоли с гранью колонны, должна быть не менее 0,002∙b∙ho. Поперечную арматуру консолей рекомендуется конструировать в виде сварных сеток с наклонными или горизонтальными поперечными стержнями, если число одинаковых консолей достаточно велико и арматура колонн сварная. Отгибы в коротких консолях рекомендуется направлять из нижнего угла консолей в противоположный верхний угол. При большом вылете или при большой высоте консоли допускается делать отгибы соответственно под углом 30 о или 60 о или размещать отгибы в двух плоскостях, располагая каждую плоскость под углом 45 о. При большом числе прямых и отогнутых стержней верхние и нижние участки отгибаемых стержней допускается размещать во втором ряду. Концы продольной арматуры растянутой зоны односторонней консоли, расположенной в пределах высоты колонны, должны быть заведены за грань колонны на величину lан и в любом случае должны быть доведены до противоположной грани колонны. 46. Расчет двухветвевых колонн. Конструирование Колонны каркасного здания могут быть сплошными прямоугольного сечения или сквозными двухветвевыми. Сквозные колонны имеют в нижней подкрановой части две ветви, соединенные короткими распорками-ригелями. Для средних колонн в нижней подкрановой части допускают смещение оси ветви с оси подкрановой балки. Распорки размещают так, чтобы размер от уровня пола до низа первой надземной распорки составлял не менее 1,8 м и между ветвями обеспечивался удобный проход. Нижнюю распорку располагают ниже уровня пола. Высоту сечения распорки принимают (1,5…2) h, а ширину — равной ширине сечения ветви. Расчет: H зд 14,4 м Привязка всегда 250мм. Статический расчет не отличается от статического расчета для сплошных колонн. Для стат расчета определяется приведенный момент инерции. Подкрановая часть представляет из себя раму, кот разбивается на отдельные рамы. При расчете определяется приведенная гибкость: red где: 1 12 4l02 2S 2 2 C2 hв 2 -гибкость распорок; l0 - расчетная - расстояние между ветвями; S - шаг распорок; h - - гибкость ветвей; высота всей ветви; C высота одной ветви 2 2 Если нужен учет продольного изгиба: e Ncnt M N e0 e ea 1 N N crit Для каждой ветви определяется усилие, приходящееся на каждуюю ветвь: 1 N M 2 C Nв Расчет ведется для наиболее сжатой ветви, а если одна ветвь растянута, то всю поперечную силу передают на одну сжатую ветвь M VS 4 По данному M и N момент M VS 2 определяется армирование(как и для сплошного сечения). Распорка рассчитывается на и работает как изгибаемый элемент(действует только момент). Ар-ра в ветвях принимается симметричная по наиболее загруженной ветви. 47. Расчет и конструирование консолей колонн(см. методу на всякий случай!) Консоли в колоннах устраивают с целью создания необходимой площадки для опирания различных примыкающих к колонне на разных уровнях конструкций (ферм, подкрановых балок, ригелей, прогонов). Консоли могут быть односторонние и двусторонние. Последние следует устраивать в одной плоскости, особенно в сборных колоннах. При вылете 100-150 мм консоль может не иметь вута и конструироваться прямоугольной. При вылете более 150 мм консоль должна иметь вут с углом наклона величиной 45 о. Ширина консоли должна быть равной ширине колонны. Исключение могут составлять консоли, устраиваемые в широких подколонниках для опирания фундаментных балок. Высота консоли и ее арматура назначаются по расчету. Консоли армируются поперечной и продольной арматурой. Поперечная арматура коротких консолей при сварных и вязаных каркасах колонн конструируется следующим образом: — при h 2,5 a - в виде наклонных хомутов по всей высоте консоли; — при h 2,5 a - в виде отогнутых стержней и горизонтальных хомутов по всей высоте консоли; — при h 3,5 a и Q Rp b h0 - в виде горизонтальных хомутов без отогнутых стержней, которые в этом случае допускается не предусматривать; здесь ho принимается в опорном сечении консолей. Во всех случаях шаг хомутов должен быть не более h/4 и не более 150 мм; диаметр отогнутых стержней должен быть не более 1/15 длины отгиба loтг и не более 25 мм. При этом суммарная площадь сечения наклонных хомутов и отогнутых стержней, пересекающих верхнюю половину линии длиной l, соединяющей точки приложения силы Q и сопряжения нижней грани консоли с гранью колонны, должна быть не менее 0,002∙b∙ho. Поперечную арматуру консолей рекомендуется конструировать в виде сварных сеток с наклонными или горизонтальными поперечными стержнями, если число одинаковых консолей достаточно велико и арматура колонн сварная. Отгибы в коротких консолях рекомендуется направлять из нижнего угла консолей в противоположный верхний угол. При большом вылете или при большой высоте консоли допускается делать отгибы соответственно под углом 30 о или 60 о или размещать отгибы в двух плоскостях, располагая каждую плоскость под углом 45 о. При большом числе прямых и отогнутых стержней верхние и нижние участки отгибаемых стержней допускается размещать во втором ряду. Концы продольной арматуры растянутой зоны односторонней консоли, расположенной в пределах высоты колонны, должны быть заведены за грань колонны на величину lан и в любом случае должны быть доведены до противоположной грани колонны. Расчет и сравниваем с Vsd A s, req- площадь продольной арматуры, требуемая по расчету; A s, prov- принятая площадь продольной арматуры. 48,49 Фундаменты ОПЗ. Общие принципы расчета и конструирования Фундамент – это часть здания, расположенного ниже уровня земли и предназначенного для передачи и перераспределения нагрузок на основание. Классификация: А) По способу изготовления: – монолитные; – сборные; – цельно составные. Б) По конструктивным особенностям: – ленточные (под рядами колонн в одном или в двух направлениях); – отдельные (под каждой колонной); – сплошные плитные (под всем сооружением). В) По глубине заложения: – мелкого; – глубокого; – свайные. Внецентренно нагруженные фундаменты проектируются прямоугольными в плане, вытянутыми в направлении действия изгибающего момента и отношения a 0,60, 7. сторон b Тип фундамента выбирают, исходя из их стоимости, расхода материалов и трудоемкости с учетом эксплуатационных и конструктивных требований. Отдельные фундаменты устраивают при относительно небольших нагрузках и достаточно редком расположении колонн. При больших нагрузках и относительно слабых грунтах делают ленточные фундаменты. Ленточные фундаменты особенно целесообразны при неоднородных грунтах и различных нагрузках. Если несущая способность грунтового основания фундаментов недостаточна, устраивают сплошные фундаменты (например, под высотные каркасные здания, сооружения башенного типа и т. п.). Расчет отдельного центрально-нагруженного железобетонного фундамента. Под центрально-нагруженными понимают фундаменты, испытывающие воздействие внешней силы N, приложенной по отношению к центральной оси фундамента с e e 0 a . Центрально-нагруженные фундаменты обычно выполняют эксцентриситетом квадратными в плане, за исключением случаев, когда они могут быть развиты во все стороны из-за близости других подземных сооружений. Расчет фундамента состоит из двух частей: расчета основания (определяют форму и размеры подошвы) и тела фундамента (высоту фундамента, размеры его ступеней и сечения арматуры). Расчет основания фундамента. Определение размеров подошвы фундамента производят при допущении, что реактивное давление на грунт по подошве фундамента распределяется по линейному закону. 50. Расчет фундаментов на продавливание Одним из предельных состояний фундамента является его продавливание колонной. Опытным путем установлено, что разрушение фундамента от продавливания происходит по боковым поверхностям усеченной пирамиды (рис. 48). Рис. 48. Расчетная схема продавливания фундамента: 1 – колонна; 2 – пирамида продавливания Разрушающие внутренние усилия возникают в сечениях железобетонного фундамента под углом к основанию. Так как давление грунта равномерно распределено по всей поверхности подошвы фундамента, а вертикальная нагрузка от колонны в момент продавливания будет передаваться на грунт только через основание пирамиды продавливания, то можно вычислить продавливающую силу, как неуравновешенную часть вертикальной нагрузки , (7.6) где – давление грунта; пирамиды. – площадь фундамента; – площадь основания пирамиды продавливания; – размеры основания Как следует из рисунка 48, размеры основания пирамиды продавливания легко вычисляются колонны. , , (7.7) где – размеры поперечного сечения По боковым граням пирамиды продавливания будут возникать растягивающие напряжения. С учетом этого, можно записать условие прочности фундамента на продавливание (рис. 49) , (7.8) где – расчетное сопротивление бетона растяжению; – площадь боковой поверхности пирамиды продавливания. Рис. 49. Расчетная схема условия прочности на продавливание Площадь боковой поверхности пирамиды продавливания можно вычислить по следующей формуле , (7.9) где продавливания. – длина средней линии боковой поверхности пирамиды После подстановки (7.9) в (7.8) получим 51. Расчет и конструирование стаканной части фундамента 1. Определение размеров подколонника: Для надежной анкеровки продольной арматуры колонны она должна быть заведена в стакан фундамента на длину не менее lbd. As ,req (106.1) lbd 1 2 3 4 lb lb,min , As , prov Где As,req — площадь продольной арматуры, требуемая по расчету; As,prov — принятая площадь продольной арматуры колонны. 1 2 3 4 принимаются по таблице СНБ 5.03.01-02 в зависимости от условий анкеровки, работы арматурных стержней: растянутые или сжатые. lb,min = max(0,6 lb; 15 ; 100 мм) (106.2) lb–величина базовой длины анкеровки lb = По конструктивным соображениям заглубление колонны в стакан фундамента должно быть не менее высоты сечения колонны. Определяем требуемое расстояние от дна стакана до низа подошвы фундамента из условия продавливания колонной фундамента от дна стакана. Расчет внецентренно нагруженных стаканных фундаментов, прямоугольных в плане, производится на действие расчетной продольной силы, действующей в уровне торца колонны Тогда давление грунта на подошву фундамента - Площадь подошвы фундамента Определяем вспомогательный коэффициент Требуемое из условия продавливания значение рабочей высоты определяется по формуле Тогда полная высота фундамента должна быть не менее hf = hg + d + 50 Принимаем полную высоту фундамента кратной 300 мм Назначаем размеры подколонника в плане, принимая их кратными 300мм. в направлении x – hcf = hc + 2 × 75 + 2 × 225 в направлении y – bcf = bc + 2 × 75 + 2 × 225 hc ,bc-размеры сечения колонны в плане Минимальная толщина стенок стакана поверху равна 225 мм. 2. Расчет армирования стаканной части фундамента Проверка прочности бетонных ижелезобетонных подколонников производится по двум сечениям по их высоте: Прямоугольно госечения в уровне плитной части (сечение 1-1); коробчатого сечения стаканной части в уровне заделанного торца колонны (сечение 22). Расчет прямоугольных сечений 1-1 производится на следующие величины расчетных усилий (вычисленных с учетом веса подколонника и нагрузок от опирающихся на него фундаментных балок): продольную силу N, изгибающие моменты Мx и Мy. Расчет коробчатого сечения 2-2 производится на продольную силу N-Nc и изгибающие моменты Мx, Мy (в уровне заделанного торца колонны). Требуемая площадь продольной арматуры определяется по формуле Процент армирования но не менее при этом ρλ принимается не менее 0,10% и не более 0,25% Требуемая площадь поперечной арматуры определяется по формуле Где zi – расстояние от торца колонны до сеток поперечного армирования Поперечное армирование сетками устанавливаем в пределах верхней части стакана по длине Первую сетку устанавливаем на расстоянии 50 мм от верхнего обреза фундамента, вторая сетка – на расстоянии 50 мм от первой, далее сетки с шагом 150мм по высоте. 52. Предпосылки и допущения при определении ширины раскрытия трещин Предпосылки и допущения, принятые в методе определения ширины раскрытия трещин: 1. В общем случае ширина раскрытия трещин принимается равной средним деформациям продольной растянутой арматуры на участке между трещинами, умноженными на среднее расстояние между трещинами. w sm rm . (5.1) 2. Среднее расстояние между трещинами следует определять из условия, по которому разность усилий в растянутой арматуре в сечении с трещиной уравновешивается силами сцепления на этом участке и принимается равной усилию, воспринимаемому растянутым бетоном, или образованием трещин. 3. Деформации растянутой арматуры εst в сечении с трещиной определяются в общем случае из системы расчета уравнений деформационной модели по заданному значению моментов и продольных сил от соответствующей комбинации усилий. 4. Деформации растянутой арматуры допускается определять из упругого расчета. Для сечения с трещиной принимаем условно упругую работу бетона с приведенным модулем упругости и упругую работу арматуры со своим модулем упругости. 5. Для изгибаемых элементов прямоугольного, таврового и двутаврового сечения с арматурой, расположенной у наиболее растянутой и сжатой грани элемента, определение εst в сечении с трещиной допускается производить по упрощенной схеме, рассматривая железобетонный элемент в виде сжатого пояса бетона и растянутого пояса арматуры с равномерно распределенным напряжением по высоте поясов. С учетом принятых предпосылок, расчетная ширина раскрытия трещин определяется по формуле (8.6) СНБ 5.03.01-02: (5.2) wk smrm . По ТКП EN раздел 7.3.4: wk sr,max (sm cm ) , (5.3) Sr,max —максимальное расстояние между трещинами, определяется по формуле: sr,max k 3 c k1 k 2 k 4 где l,eff , l,eff As ; A c,eff (5.4) (5.5) Аs — площадь сечения арматуры, заключенная внутри эффективной площади растянутой зоны бетона; εsm и εcm — средние относительные деформации арматуры и бетона между трещинами. 53. Классификация предварительно напряженных конструкций Предварительно напряженные конструкции могут быть классифицированы по след. Признакам: По методу изготовления: 1) С натяжением на упоры 2) С натяжением арматуры на бетон 3) Самонапряжение 4) Сборно-монолитные( с обетонированными предварительно напряженными сборными элементами) Способы натяжения: 1) Механический 2) Электротермический 3) Комбинированный 4) Физмко-химический По принципу действия напряженного армирования 1) Одноосно предварительно напряженные 2) Двуосно предварительно напряженные 3) Объемно предварительно напряженные По степени предварительного напряжения: 1) полное преднапряжение, если при действии эксплуатационной нагрузки напряжение в бетоне наиболее растянутых волокон сечения (как правило, на уровне напрягаемой арматуры) равны нулю. 2) Если растягивающие напряжения в бетоне не превышают допустимых значений, говорят об ограниченном предварительном напряжении. 54. Усилие, приводящее к образованию трещин в предварительно напряженном элементе (формула) При расчете по предельным состояниям второй группы следует рассматривать следующие нормативные значения усилия предварительного обжатия Pk,sup = rsup Pm,t , (9.32) Pk,inf = rinf Pm,t . (9.33) В формулах (9.32)—(9.33) приняты следующие обозначения: Pm,t среднее значение усилия предварительного напряжения к моменту времени t > t0 Pk,inf нижний предел усилия предварительного напряжения в эксплуатационной стадии Pk,sup верхний предел усилия предварительного напряжения в эксплуатационной стадии Pd — расчетное значение усилия предварительного обжатия; р — частный коэффициент безопасности для усилия предварительного обжатия, принимаемый равным: при благоприятных эффектах, создаваемых предварительным напряжением (например, повышение устойчивости) — 0,9 или 1,0; то же, при неблагоприятных эффектах (например, расчет прочности конструкции в момент передачи усилия обжатия) — 1,2 или 1,0. Допускается принимать р = 1,0; rsup — коэффициент, определяющий верхний предел значения усилия предварительного обжатия при расчетах по предельным состояниям второй группы, принимаемый равным 1,05 — для конструкций с натяжением арматуры на бетон и без сцепления с бетоном, 1,1 — при натяжении на упоры; rinf — коэффициент, определяющий нижний предел значения усилия предварительного обжатия при расчетах по предельным состояниям второй группы, принимаемый равным 0,95 — для конструкций с натяжением арматуры на бетон и без сцепления, 0,9 — при натяжении на упоры. В сечениях предварительно напряженных элементов, в которых на стадии изготовления могут образоваться закрывающиеся либо незакрывающиеся трещины от усилия предварительного обжатия, ширина их раскрытия не должна превышать wlim = 0,2 мм. Все растягивающие усилия в сечении в начальной ситуации должны восприниматься ненапрягаемой арматурой 55. Положительные и отрицательные эффекты преднапряжения С одной стороны он имеет ряд плюсов, с другой стороны имеются и некоторые минусы. Среди основных преимуществ выделяют следующие: Является более экономичным материалом. В среднем на 40-60% сокращается расход стали, которая используется для производства арматуры. Также на изготовление уходит меньше цемента. Уменьшается сечение, следовательно становится меньше вес и объем. Посвышается стойкость к трещинообразованию и ограничивается ширина раскрытия трещин . Как следствие, предохраняет металлическую арматуру от появления коррозии. В особенности это важно для сооружений, находящихся в постоянном взаимодействии с водой (труб, резервуаров, плотин). Увеличивается жесткость конструкции (снижается деформативность, благодаря чему удается перекрывать большие пролеты, возводить сверхвысокие сооружения) Может использоваться для специальных строений, в которых нельзя или нежелательно применять типичные ЖБИ. В том числе благодаря тому, что уменьшается масса и объем, железобетон напряженный легче и проще использовать для стыков сборных частей конструкции. Это могут быть: балки кровельные и подкрановые, плиты для покрытий в помещениях промышленного назначения. Расширяется сфера применения материала. Его можно использовать не только для сборных, но и для монолитно-сборных сооружений. В этом случае его применяют только в тех участках, где наблюдается напряжение конструкции. В остальных же частях используется типичный легкий пенобетон, тяжелый бетон или монолитный железобетон. Увеличивается выносливость к-ций при многократно повторяющихся нагрузках Повышается устойчивость сжатых элементов С течением времени увеличивается сейсмостойкость напряженно-армированых конструкций. Объясняется это тем, что в процессе изготовления используются более легкие материалы для сечения. Помимо достоинств железобетон преднапряженный имеет и свои недостатки. высокую трудоемкость и сложность изготовления. Дело в том, что в процессе производства требуются тщательные расчеты. Важно также предусматривать способ транспортировки, хранения и монтажа конструкции. Если не подумать об этом заранее и не подготовить тщательный проект изготовления, то могут появиться нежелательные растягивающие или сжимающие напряжения. Они в дальнейшем приведут к аварийной ситуации. К примеру, при неравномерном обжатии в торцах конструкции могут появиться трещины, которые значительно снизят несущую способность. Из-за повышенной звуко- и теплопроводности необходимо дополнительно использовать изолирующие материалы для всей конструкции. Имеют более низкую огнестойкость, чем типичные ЖБИ. Хотя также отличается несгораемостью. Вес напряженных ЖБИ гораздо меньше массы обычных железобетонных изделий, но выше массы деревянных и металлических конструкций. 56. График изменение во времени усилия предварительного напряжения в арматуре при натяжении на упоры. РА – потери от деформации анкеров, расположенных в зоне натяжных устройств Рsl - потери, вызванные проскальзыванием напрягаемой арматуры в анкерных устройствах, происходящие на длине зоны проскальзывания х0 Рf - потери, вызванные деформациями стальной формы Рµ(х) - потери, вызванные трением арматуры о стенки каналов или о поверхность бетона конструкции Рir - потери от релаксации напряжений арматуры РТ - потери от температурного перепада, определяемого как разность температур натянутой арматуры в зоне нагрева и устройства, воспринимающего усилие натяжения при прогреве бетона Рс - потери, вызванные упругой деформацией бетона, следует определять для элементов с натяжением напрягаемой арматуры на упоры. В элементах с натяжением арматуры на бетон этот вид потерь следует учитывать только в случае последовательного отпуска напрягаемых стержней. Рt(t) - реологические потери, вызванные ползучестью и усадкой бетона, а также длительной релаксацией напряжений в арматуре 57. График изменение во времени усилия предварительного напряжения в арматуре при натяжении на бетон Рµ(х) - потери, вызванные трением арматуры о стенки каналов или о поверхность бетона конструкции Рsl - потери, вызванные проскальзыванием напрягаемой арматуры в анкерных устройствах, происходящие на длине зоны проскальзывания х0 Рс - потери, вызванные упругой деформацией бетона, следует определять для элементов с натяжением напрягаемой арматуры на упоры. В элементах с натяжением арматуры на бетон этот вид потерь следует учитывать только в случае последовательного отпуска напрягаемых стержней. Рt(t) - реологические потери, вызванные ползучестью и усадкой бетона, а также длительной релаксацией напряжений в арматуре 58.Усилие предварительного обжатия при расчете по предельным состояниям первой и второй группы предельных состояний. Среднее значение усилия предварительного обжатия Pm,t в момент времени t > t0 (с учетом всех потерь) следует определять по формулам: — при натяжении арматуры на упоры Pm,t Pm,0 Pt (t ) ; (9.28) — при натяжении на бетон Pm,t Pm,0 Pt (t ) Psp Pob , (9.29) но принимать не большим, чем это установлено условиями Pm,t 0,65fpk Ap и Pm,t P0 100Ap , (9.30) где Pm,t , P0 — в Н, Ap — в мм2 . Усилие предварительного обжатия Рт,0 к моменту времени t = t0, действующее непосредственно после передачи усилия предварительного обжатия на конструкцию (при натяжении на упоры) или после завершения натяжения (при натяжении на бетон), должно быть не более Pm,0 pm,0 Ap 0,75fpk Ap . (9.21) В формуле (9.21) величину Рт,0 определяют — для элементов с натяжением на упоры Pm,0 P0 Pc Pir P ( x ) PТ PA Pf ; (9.22) — для элементов с натяжением на бетон Pm,0 P0 Pc Pir P ( x ) Psl . Рс - потери, вызванные упругой деформацией бетона, следует определять для элементов с натяжением напрягаемой арматуры на упоры. В элементах с натяжением арматуры на бетон этот вид потерь следует учитывать только в случае последовательного отпуска напрягаемых стержней. Рir - потери от релаксации напряжений арматуры Рµ(х) - потери, вызванные трением арматуры о стенки каналов или о поверхность бетона конструкции РТ - потери от температурного перепада, определяемого как разность температур натянутой арматуры в зоне нагрева и устройства, воспринимающего усилие натяжения при прогреве бетона РА – потери от деформации анкеров, расположенных в зоне натяжных устройств Рsl - потери, вызванные проскальзыванием напрягаемой арматуры в анкерных устройствах, происходящие на длине зоны проскальзывания х0 Рt(t) - реологические потери, вызванные ползучестью и усадкой бетона, а также длительной релаксацией напряжений в арматуре. При расчете предварительно напряженной конструкции по предельным состояниям первой и второй групп следует принимать усилия предварительного обжатия, соответствующие рассматриваемой расчетной ситуации (начальная, постоянная). При расчете по предельным состояниям первой группы Pd = pPm,t . (9.31) При расчете по предельным состояниям второй группы следует рассматривать следующие нормативные значения усилия предварительного обжатия Pk,sup=rsup Pm,t , (9.32) Pk,inf = rinf Pm,t . (9.33) Pd — расчетное значение усилия предварительного обжатия; р — частный коэффициент безопасности для усилия предварительного обжатия, принимаемый равным: при благоприятных эффектах, создаваемых предварительным напряжением (например, повышение устойчивости) — 0,9 или 1,0; то же, при неблагоприятных эффектах (например, расчет прочности конструкции в момент передачи усилия обжатия) — 1,2 или 1,0. Допускается принимать р = 1,0; rsup — коэффициент, определяющий верхний предел значения усилия предварительного обжатия при расчетах по предельным состояниям второй группы, принимаемый равным 1,05 — для конструкций с натяжением арматуры на бетон и без сцепления с бетоном, 1,1 — при натяжении на упоры; rinf — коэффициент, определяющий нижний предел значения усилия предварительного обжатия при расчетах по предельным состояниям второй группы, принимаемый равным 0,95 — для конструкций с натяжением арматуры на бетон и без сцепления, 0,9 — при натяжении на упоры. 59.Формула определения нормальных напряжений в бетоне при его обжатии. 60.Особенности расчета предварительно напряженных конструкций по первой группе предельных состояний. 61. Особенности расчета элементов по предельным состояниям второй группы Расчет предельных состояний второй группы при действии изгибающих моментов и продольных сил необходимо рассматривать в двух стадиях: - стадию декомпрессии ( погашение начальных сжимающих напряжений в бетоне на уровне центра тяжести напрягаемой арматуры, вызванных предварит. напряжением) - стадию трещинообразования ( после погашения начальных сжимающих напряжений в бетоне, вызванных ПН ) Предельные состояния второй группы затрудняют нормальную эксплуатацию конструкций и связаны с ограничением: а) чрезмерных деформаций и перемещений, неблагоприятно воздействующих на внешний вид конструкции, затрудняющих протекание технологических процессов, создающих повреждения отделки и других неконструктивных (декоративных и вспомогательных) элементов; б) недопустимого трещинообразования в бетоне конструкции, неблагоприятно влияющего на ее внешний вид и долговечность; в) вибрационных воздействий, создающих дискомфорт для людей, повреждения зданий или их частей. При расчете по предельным состояниям второй группы проверяется общее условие, согласно которому значения расчетных эффектов, вызванных воздействиями Ск (например, ширина раскрытия трещин или прогибы) не должны превышать допустимых значений, установленных нормативным документом: Ск [Сlim ] где Ск - расчетное значение прогиба или ширины раскрытия трещин, Сlim - допустимое значение прогиба или ширины раскрытия трещин установленное нормативным документом с точки зрения обеспечения нормальных условий эксплуатации конструкции. Трещиностойкость - способность железобетонной конструкции сопротивляться образованию и раскрытию трещин. Трещины в бетоне конструкций образуются уже в процессе формирования структуры в результате развития физико-химических процессов, происходящих при твердении цемента. Образование и чрезмерное раскрытие трещин, помимо того, что снижает жесткость элемента - приводит к возрастанию прогибов, вызывает неудобства эстетического восприятия, но главное оказывает существенное влияние на долговечность конструкций здания или сооружения. Наличие трещин большой ширины раскрытия создает условия, при которых развивается коррозия стальной арматуры. Расчет по раскрытию трещин следует производить из условия: wk wlim , Расчетную ширину раскрытия трещин wk, нормальных к продольной оси, следует определять по формуле: wk =srmsm , где srm - среднее расстояние между трещинами; sm - средние относительные деформации арматуры, определяемые при соответствующем сочетании нагрузок; srm-среднее расстояние между трещинами Общие положения 9.8.1.1 Расчет предварительно напряженных элементов по образованию трещин, нормальных к продольной оси элемента, при действии изгибающих моментов и продольных сил в общем случае следует производить по деформационной модели При расчете по образованию трещин в расчетных уравнениях деформационной модели следует учитывать начальные относительные деформации напрягаемой арматуры, а усилие предварительного обжатия рассматривать как внешнюю силу, приложенную к сечению. 9.8.1.2 Усилие предварительного обжатия следует вводить в расчет с учетом потерь предварительного напряжения 9.8.1.3 Критерием исчерпания трещиностойкости сечения, нормального к продольной оси элемента, следует считать достижение крайним растянутым волокном бетона сечения предельных деформаций растяжения. 9.8.1.4 Расчет трещиностойкости элементов прямоугольного, таврового и двутаврового сечений с арматурой, сосредоточенной у наиболее растянутой и сжатой граней, когда внешние усилия действуют в плоскости оси симметрии сечения, допускается производить исходя из условно упругой модели сечения. 62.Минимальное количество напрягаемых стержней в растянутой зоне требования к их анкеровке. Размещение арматуры в сечении 1 Расстояния в свету между стержнями (при натяжении арматуры на упоры) или оболочками канатов напрягаемых элементов при натяжении на бетон по высоте и ширине сечения должны назначаться с учетом направления, удобства укладки и уплотнения бетонной смеси, степени местного обжатия бетона, габаритов натяжного оборудования, концевых анкеров 2 При стесненных условиях допускается располагать стержни попарно (без зазора между ними). Такая пара стержней при назначении расстояния между парами стержней сi или длины анкеровки должна рассматриваться как условный стержень диаметром red 12 22 (где 1 и 2 — диаметры сближенных попарно стержней, см. рисунок 11.13). В предварительно напряженных констр-х, независимо от способа натяжения арм-ры следует обеспечивать её надежную анкеровку на концевых участках. Полную расчетную длину анкеровки напрягаемой арматуры при ее натяжении на упоры следует определять по формуле lbpd 1,2lpt 2 pd p fbpd , где pd — напряжения в арматуре от действия нагрузок; р — предварительные напряжения в арматуре с учетом всех потерь; lpt — базовая длина зоны передачи напряжений, определяемая по формуле В торцах предварительно напряженных конструкций следует предусматривать установку дополнительной поперечной (напрягаемой или ненапрягаемой) или косвенной арматуры (сетки, каркасы) с учетом следующих требований: дополнительная арматура устанавливается на участке длиной не менее 0,6lbp в к-х из тяжелого бетона; шаг дополнительной арматуры в изделиях из легкого бетона д.б. не более 50 мм, а из тяжелого бетона 50-100 мм ненапрягаемая поперечная арматура должна быть надежно закреплена приваркой к закладным деталям на участке длиной не менее 1/4 высоты торцевого сечения; сечение ненапрягаемой поперечной арматуры определяется из условия восприятия не менее 20 % усилия в продольной напрягаемой арматуре, а для конструкций, рассчитываемых на выносливость, — не менее 30 %; напрягаемая поперечная арматура устанавливается из условия возможности получения усилия обжатия величиной не менее 15 % от усилия обжатия торцевого сечения с продольной напрягаемой арматурой, расположенной у верхней и нижней граней сечения элемента