Документ 624947

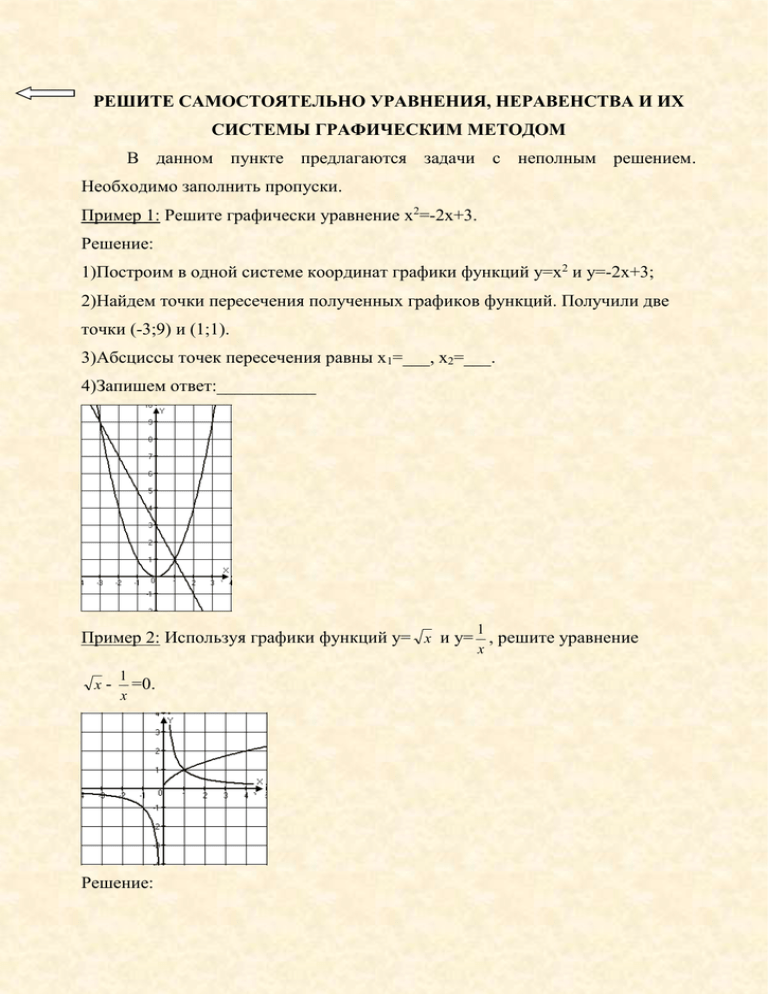
РЕШИТЕ САМОСТОЯТЕЛЬНО УРАВНЕНИЯ, НЕРАВЕНСТВА И ИХ
СИСТЕМЫ ГРАФИЧЕСКИМ МЕТОДОМ
В данном пункте предлагаются задачи с неполным решением.
Необходимо заполнить пропуски.
Пример 1: Решите графически уравнение х2=-2х+3.
Решение:
1)Построим в одной системе координат графики функций у=х2 и у=-2х+3;
2)Найдем точки пересечения полученных графиков функций. Получили две
точки (-3;9) и (1;1).
3)Абсциссы точек пересечения равны х1=___, х2=___.
4)Запишем ответ:___________
1
х
Пример 2: Используя графики функций у= х и у= , решите уравнение
х-
1
=0.
х
Решение:
1
х
1)Используя графики функций у= х и у= , можно заметить, что графики
пересекаются в единственной точке (__;__);
2)Абсцисса точки пересечения равна ___;
3)Запишем ответ:____
Пример 3: Используя график функции у=х2 - 2х, решите неравенство х2 - 2х  0.
Решение:
1)Пользуясь данным графиком, видим, что график
функции у=х2 - 2х лежит выше оси Ох на промежутках
(__;__]  [__;__). Следовательно, х  (__;__]  [__;__);
2)Запишем ответ:______________
Пример 4: Решите неравенство –х2+3х>|x-1| графически.
Решение:
1)Построим графики функций у=–х2+3х и у= |x-1| в одной системе координат;
2)На оси Ох найдем промежутки, на которых график функции у= –х2+3х лежит
________графика функции у=|x-1|. Видим, что х  (__;__);
3)Запишем ответ: ____________
Пример 5: На рисунке изображена парабола и три прямые. Укажите систему
уравнений, которая имеет два решения.
у  1 х2
1) 
х  у  4
;
у  1 х2
2) 
;
х  4  0
у  1 х2
3) 
у  5  0
;
4) Такой системы нет
Решение:
1)Анализируя задание, можно сказать, что графики функций должны
пересекаться в двух точках.
2)Пользуясь рисунком, видно, что в двух точках пересекаются графики
системы №____;
3)Запишем ответ: №____.
Пример 6: На рисунке изображены графики функций у=х2 – 2х – 3 и у=1 – 2х.
 у  х 2  2х  3
.
 у  1  2х
Используя графики, решите систему уравнений 
Решение:
1)Анализируя рисунок, видим, что графики функций пересекаются в двух
точках с координатами (2;-4) и (-2;5). Следовательно, система уравнений имеет
_____ решения.
2)Запишем ответ: ______________
назад