Informatika

И.А. Пахнутов
ИНФОРМАТИКА
с элементами
программирования
Учебное пособие для студентов
младших курсов высших учебных заведений
Калининград
Издательство ФГБОУ ВПО «КГТУ»
2012
2
УДК 519.85:681.3.06(075)
УТВЕРЖДЕНО
Ректором ФГБОУ ВПО
«Калининградский Государственный
Технический университет»
АВТОР - Пахнутов И.А., к. ф.-м. н., доцент кафедры прикладной
математики Калининградского государственного технического
университета
Учебное пособие содержит основной материал для проведения
учебных (как лекционных, так и лабораторных) занятий по курсу
"Информатика", предназначено студентам младших курсов технических вузов и университетов. Материал курса расчитан на два семестра
аудиторной работы и включает некоторые разделы информационных
технологий. Материал пособия предполагает знакомство с базовыми
понятиями предмета в объеме стандартной школьной программы по
информатике.
Учебное пособие рассмотрено и одобрено кафедрой прикладной
математики ФГБОУ ВПО «Калининградский Государственный Технический университет» 20 февраля 2012 г., протокол № 7
Учебное пособие рекомендовано к изданию методическим
советом факультета фундаментальной подготовки 19 марта 2012 г.,
протокол № 8.
РЕЦЕНЗЕНТ - кафедра прикладной математики Калининградского
государственного технического университета
© ФГБОУ ВПО «Калининградский государственный технический университет», 2012 г.
3
Bведение
Интеллектуальный и технический бум конца ХIХ - начала ХХ века
породил массу новых разделов наук, так и новых наук вообще. При
этом резко проявилась тенденция ученых к получению фундаментальных знаний, основ, базиса, попытки найти основные кирпичики знания, на которых строится (уже вследствие логики) все существующее
здание науки. Нарастал информационный бум. И в этом также следовало разобраться. Что такое информация? Это, скорей всего, сообщение об изменениях в окружающей обстановке, т.е. должен быть носитель информации (сообщения), источник, передатчик, приемник информации, канал связи и т.д. Информация меняет наше отношение к окружающей действительности. Важна сравнительная оценка новизны:
если не сообщается ни о каких изменениях (как было, так и есть), то не
передается никакой информации (хотя все этапы передачи работают).
Тем не менее, и в этом случае считается, что отсутствие информации –
также является информацией (сообщением о том, что ничего нового не
произошло).
Логики выяснили, что, в принципе, любую информацию можно
получить, задавая "элементарные" вопросы, на которые достаточно отвечать лишь "да" или "нет". Каждый такой вопрос позволяет получить
минимальный объем информации, называемый битом. Наименьшее
количество элементарных вопросов, позволяющее получить необходимую информацию, определяет объем этой информации в битах. Например, чтобы угадать любое из первых 16 натуральных чисел, достаточно задать лишь четыре элементарных вопроса типа: "будет ли число меньше 9?". Если "нет", то "будет ли число меньше 13?" и т.д. Таким образом, информация о числах в этом диапазоне имеет объем 4
бит. Аналогично можно оценить объем информации о буквах, словах,
цвете, картине, поэтическом произведении и т.д.
Каждый элементарный ответ можно обозначить цифрой 0 или 1 для
"нет" и "да" соответственно. Поэтому произвольную информацию
можно записать последовательностью нулей и единиц, а количество
занятых при этом разрядов определяет количество бит информации.
Всякое целое число также представляется последовательностью нулей
и единиц в соответствии с тем, есть ли в представлении этого числа
необходимая степень двойки. Например, число 27 можно записать в
этих терминах так:
27 = 16 + 8 + 2 + 1 = 124 + 123 + 022 + 121 + 120 ,
4
последовательность коэффициентов этого двоичного представления
есть 11011, что и является представлением числа 27 в системе счисления с основанием 2. Информация о таком числе имеет объем 5 бит.
Общее число символов, используемых в повседневной практике
европейца, обычно не превосходит 256, что имеет объем 8 бит. В силу
этого, либо в силу того, что первоначальные устройства обработки информации работали с восемью разрядами нулей и единиц, этот объем
получил отдельное название байт, так что байт это 8 бит. В дальнейшем объем используемой информации возрастал быстрыми темпами,
так что пришлось пользоваться единицей в 1К=1024 байт = 210 байт
(килобайт), далее, в 1М = 220 (мегабайт), а также десятки, сотни и
тысячи мегабайт (гигабайты).
Итак, каждое число можно заменить последовательностью нулей и единиц. Это дало мощный толчок к исследованию основ арифметических и логических операций, теории алгорифмов. Было показано, что алгоритмически всякое арифметическое действие сводится к
последовательности логических операций над нулями и единицами и
сдвигу регистра (т.е. фиксированного набора нулей и единиц). Пост и
Тьюринг (США и Англия) сконструировали формально-логическую
структуру, выполняющую простейший набор логических операций, в
которой (привлекая теорию алгорифмов и формальных машин) можно
запрограммировать любую арифметическую и логическую операцию
(программы, правда, могли быть довольно длинными). К 30-м годам
20 века технология была развита достаточно для того, чтобы простейшие операции (типа тех, что рассматривали Пост и Тьюринг) можно
было легко реализовать в электронных схемах (ноль соответствует отсутствию потенциала, единица - его наличию). Тем не менее, лишь в
40-х годах были созданы первые электронные вычислительные машины (ЭВМ), которые могли выполнять около тысячи арифметических
операций в секунду. Позже согласились с тем, что поскольку простейшая логическая операция выполняется за один такт генератора частоты ЭВМ, быстродействие машины можно оценивать частотой этого
тактового генератора.
В конце 50-х годов к изготовлению блоков ЭВМ стали привлекать полупроводники, а в конце 60-х и микросхемы. Физический объем ЭВМ значительно уменьшился (при увеличившемся объеме постоянной и оперативной памяти). В начале 80-х годов ЭВМ уже начали
изготавливать на основе целых интегральных блоков – больших интегральных схем (БИС), что позволило создать компактные ЭВМ и персональные ЭВМ. Тактовая частота таких устройств уже превосходила
500 мегагерц (5108 герц). При этом обрабатываемая информационная
плотность  = объем оперативной памяти на 1 см3 вычислительного
устройства росла очень быстро (похоже, экспоненциально), такие же
5
темпы сохраняются и сейчас, так что предсказание очередного этапа
развития компьютерной технологии весьма затруднительно.
С точки зрения программного обеспечения прогресс происходил
не менее быстро. На первых этапах при невысокой производительности ЭВМ нужно было дефицитную память использовать лишь на конкретные нужды потребителя, так что приходилось программировать
решение задач непосредственно в терминах машинных приказов. Постепенно оказалось возможным часть выросшей памяти отдать под
разного рода "благоустройства". Появился язык команд и макрокоманд Ассемблер и Макроассемблер. Появились языки программирования, позволяющие отдавать приказы машине в терминах, близких к
логической структуре решения задачи и к естественному алгоритму
(Фортран, Лисп, Кобол, Алгол, и т.д.), а соответствующие трансляторы, переводя алгоритмы с языка программирования на язык кодов, непосредственно доступных процессору ЭВМ, создавали довольно приличные исполняющие программы, близкие к тому, что могли бы создать программисты непосредственно. Оказалось возможным создать
языки, позволяющие интерпретировать каждый приказ прямо в кодах
ЭВМ (Бейсик и расширения), а также глубоко структурированные
языки, имеющие вначале чисто учебную цель, развитые в дальнейшем
до профессионального уровня (Паскаль), и приспособленные для различных целей системного программирования (Си, Си++ и др.). Появилась тенденция создавать программное обеспечение ЭВМ в части
его взаимодействия с пользователем (интерфейс) так, чтобы от пользователя требовались лишь минимальные знания в области информационной культуры и практически нулевые в области программирования.
При этом всякое нажатие клавиши, щелчок кнопкой "мыши", сопровождается подсказкой, соответствующей строкой меню, звуковым сигналом и т.д., так что в некоторых случаях (к сожалению, многих) умение ориентироваться в этих окнах-подсказках принимается за информационную грамотность. Для повседневного потребителя современных "бытовых" технологий этого вполне достаточно. Для будущих
инженеров, экономистов и специалистов других отраслей знания необходимо больше. Во-первых, никакой набор инструментальных
средств не может быть универсальным, и всегда в практической
деятельности может появиться проблема, которую (пусть с помощью
компьютера) следует решать некоторым специальным образом с
привлечением доступных средств программирования. Во-вторых,
процесс использования алгоритмических языков и других средств
программирования вынуждает человека к творчеству, активизирует
умственную деятельность, "упорядочивает мозги" и с учебной целью
(по крайней мере) обучение программированию весьма полезно.
6
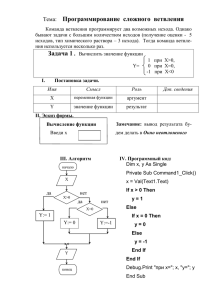
Всякой разумно составленной программе предшествует анализ
проблемы, возможное расчленение ее на более простые части с выяснением взаимосвязей этих частей (специалисты говорят: "понимаю –
значит, могу запрограммировать"). Схематическое представление этих
частей, использующее принятые визуальные и графические средства,
представляет собой блок-схему задачи. Это помогает разобраться в
постановке задачи и выделить основные этапы ее решения. Отдельный
элемент блок-схемы при дальнейшем анализе может быть представлен
своей, более подробной, блок-схемой (детализация), и т.д. до тех пор,
пока каждый отдельный блок при достаточной его очевидности не
сможет быть записан алгоритмически в каком-нибудь языке программирования.
Рассмотрим, например, алгоритм Эвклида нахождения наибольшего общего делителя двух многочленов: многочлен большей
степени (Pn) делим на другой (Qm) и, если остаток от деления равен
нулю, то наибольший делитель найден, в противном случае многочлен-делитель делим на остаток и т.д. Логическую схему решения
задачи можно представить в следующем виде (см. рис. 1):
Исходные
данные: Pn , Qm
ДА
НЕТ
n ≥ m?
U:= Qm
V:= Pn
mn
U:= Pn
V:= Qm
S:= U/V
R – остаток
k – степень
остатка
ДА
НЕТ
k = 0?
НЕТ
R= 0?
ДА
Общ.
делителя нет
Общий
делитель V
Рис. 1
U:= V
V:= R
n:= m
m:= k
7
(здесь прямоугольники содержат последовательность простых арифметических операций, ромбики обозначают разветвление в зависимости от логических условий). Теперь осталось позаботиться о представлении исходной информации и программировании отдельных
блоков, выбрав подходящую среду программирования.
На начальном этапе обучения информатике полезно познакомиться с одним из наиболее простых языков программирования. Здесь
будет взят для этой цели BASIC. Хотя изначально для этой цели предназначался PASCAL, однако, позднее он расширился по сравнению с
оригинальной версией Н. Вирта до весьма структурированного профессионального языка программирования, приспособленного к работе
в современных программных оболочках (Delphi). BASIC ( Beginner’s
All-purpose Symbolic Instruction Code – язык программирования общего назначения для начинающих) структурно проще, тем не менее, он
также имеет Visual – расширение, входит в состав программных оболочек Word, Excel, Acsess, Power Point, Corel Draw и др. Кроме того,
некоторые средства функционального и символьного программирования (MATHCAD, MAPLE и др.) весьма сходны по своей
конструкции с тем, что можно найти в Бейсике и легко усваиваются на
основе последнего. Это и определило тематику предлагаемого курса,
включающую в себя
1) основы алгоритмического языка BASIC;
2) введение в Visual Basic и HTML, программирование приложений;
3) программная среда МATHCAD и введение в численный анализ.
Многие языковые структуры имеют явно просматриваемую параллель в этих трех языках, многие задания решаются совершенно однотипно, поэтому в этом пособии сходные конструкции обсуждаются
параллельно, оговариваются различия и особенности реализации в том
или ином контексте.
BASIC в его исходном варианте (DOS-версия) был предназначен
для реализации непосредственного (с клавиатуры) взаимодействия
пользователя с оперативной памятью компьютера, внешними устэкран
ройствами: консоль ↗
↘вн. память , допускал непосредственный анализ
сигналов консоли (клавиатуры), изменение содержимого конкретных
адресов оперативной памяти, обработку отдельных пикселей экрана
при довольно бедной цветовой палитре, и т.д., отводя немалую роль
"ручному" управлению компьютером.
В настоящее время мощные операционные системы все эти функции берут на себя, отделяя пользователя от его непосредственного
участия в работе компьютера (в некоторых операционных системах
DOS-Basic вообще недопустим). Для решения широкого класса задач
созданы гибкие прикладные пакеты, в которых простой и доступный
8
метаязык позволяет, в основном, справиться с проблемами пользователя. В основном. В сложных ситуациях все-таки используется некоторая модификация подходящего языка программирования, приспособленная для работы в данном пакете, которая позволяет пользователю "общаться" лишь с объектами этого пакета, его структурами
(так назаваемое объектное программирование). Поэтому Visual Basic
различается в указанных выше пакетах на объектном уровне, сохраняя
свое принципиальное ядро от DOS-Basic. Это дает повод рассматривать элементы программирования в параллели Basic – Visual BASIC.
Отметим, что наиболее интенсивно Visual BASIC используется в
офисном пакете EXCEL, так что последний повсюду будет выполнять
роль "носителя" этого языка, конкретную реализацию которого будем
называть VBA (Visual Basic for Applications) в отличие от QB (Quick
Basic) – распространенной DOS-версии языка. По этой причине в
пособии не будут рассматриваться некоторые особенности языка QB,
связанные, прежде всего, с прямым воздействием на оперативную
пямять, на буфер обмена, с использованием команд ассемблера, с
графическим режимом дисплея, использованием стэков, воспроизведением (музыкальных) звуков, сегментированием программ.
MATHCAD (короче, Mcd) является платформой для непосредственных инженерных расчетов, поэтому его средства программирования ограничены лишь самыми необходимыми конструкциями. Например, полностью отсутствуют операторы программируемого ввода с
клавиатуры, вывода на экран, условного и безусловного перехода
внутри программ, разветвления типа селектора, коллекция типов переменных ограничена двумя: длинные действительные числа и строки (в
парных кавычках), все операции над массивами (размерности не
больше трех) и графиками выделены в отдельный интерфейс. Тем не
менее, богатство коллекции встроенных программ, удобство работы с
объектами непосредственно на рабочем листе, удобный и "дружественный" интерфейс делают эту платформу особенно привлекательной для конкретных инженерных расчетов и применения в исследовательской практике.
9
1. Общая часть
1.1. ОСНОВНЫЕ СТРУКТУРЫ
С точки зрения обычной грамматики в языке BASIC естественно выделить следующие структуры (ниже в уголках – название
программной части, в [  ] – необязательная часть).
Структура:
алфавит
слово
предложение
программа
Алфавит:
латинский алфавит
кириллица
десятичные цифры
арифметические знаки
знаки сравнения
разделители
специальные символы
Латинский алфавит, кириллица и десятичные цифры не требуют пояснения. Полезно лишь заметить, что поскольку рассматриваемые программные средства имеют происхождение в англоязычных странах, то
основные языковые структуры описаны в терминах латинского алфавита, использование кириллицы неестественно, в некоторых случаях
даже недопустимо. Арифметические знаки = {+, -, *, \, /, ^}, где "\" знак целочисленного деления, " ^ " - знак возведения в степень. Знаки
сравнения = {<, =, >, =>, <=, <>}. Разделители = {"пробел", "enter –
перевод строки", =, .,",", ;, :, [, ], (, )} и др. (начало строки тоже можно
считать разделителем). Специальные символы = { %, !, #, $, &, @, ?, ',
_} и др. (первые пять символов позволяют явно указать тип переменной). Последовательность символов, не содержащую разделителей,
следует называть словом или лексемой.
10
Слово:
число
строка
имя
служебное слово
метка
оператор
арифметическое выражение
комментарий
Число
целое без знака
знак: -,+
вещественное без знака
Целое без знака есть конечная последовательность цифр (длина последовательности определяется форматом соответствующего типа).
Целое число может иметь предваряющий знак "+" или "-".
Вещественное без знака – целое без знака, либо два целых без знака,
разделенных (десятичной) точкой. Вещественное без знака может
заканчиватьсч масштабным множителем вида EN, где N – целое со
знаком, обозначающим степень десяти. Например, 2.381E-3 представляет вещественное число 2.38110-3 = 0.002381.
Вещественное число может иметь перед собой знак "-".
Строка есть произвольная последовательность символов (кроме
кавычек), заключенная в кавычки.
Имя можно определить как последовательность латинских букв, возможно и цифр, начинающаяся с латинской буквы. Имя может содержать и знак подчеркивания. Никакие другие символы, в том числе
разделители, не допускаются. Имя переменной, константы, функции,
подпрограммы, оператора часто называют идентификатором.
Служебное слово – слово, участвующее в формировании операторов и
управлении вычислительным процессом; смысл служебного слова не
может быть изменен в программе.
Примеры некоторых служебных слов: AND, AS, BEEP, OR, XOR,
NOT, CASE, DO, ELSE, FOR, GET, GO, IF, IN, IS, LIST, NEXT, OPEN,
PUT, RUN, SET, и др.
11
Метка
целое без знака
пробел
идентификатор
:
Метка начинает строку операторов при необходимости обращения к
ней из программы.
Оператор
приказ машине
для исполнения
(
)
служебное слово
разделитель
В качестве разделителя чаще всего используется пробел, двоеточие,
переход на новую строку.
Арифметическое
выражение
вычислимая арифметическая
формула
идентификатор
Поскольку значение логической формулы также заносится в память с
помощью оператора присваивания, то ее также естественно включить
в арифметическое выражение.
Комментарий – произвольная последовательность символов, начинающаяся с апострофа или служебного слова REM, продолжающаяся
до конца текущей строки. Комментарий не рассматривается интерпретатором и не влияет на объем исполняемой программы.
Предложение – последовательность слов и разделителей, логически
связанная последовательность операторов, размещаемая в одной строке.
Программа – последовательность предложений. В рассматриваемых
ниже приложениях программы оформляются различно.
QB: программа записывается текстом на рабочем поле редактора
и запускается выбором пункта "Run" в меню запуска, либо нажатием
клавиши "F5" консоли. Интерпретатор запускает выполнение каждого
приказа с первой строки до последней (при отсутствии ошибок) и останавливается.
VBA: в приложениях программа записывается между служебными словами "SUB ‹имя программы›()" и "END SUB" (блок с операторными скобками) и размещается на кодовой странице приложения,
либо в программном модуле. Запускается программа аналогично QB
либо из меню "Пуск" (команда "Run"), либо нажатием клавиши F5
консоли (предварительно выделив имя программы), либо подходящим
элементом управления.
12
Mcd: программа оформляется на рабочем листе в виде отдельной
процедуры, функции или отдельного блока с указанием возвращаемых
величин. Запустить ее можно, поставив после имени программы или
программного блока знак "=" (с консоли), побуждающий интерпретатор к вычислению.
Нужно при этом иметь в виду следующее: в любом языке программирования (конечно же, и в VBA) любое арифметическое выражение должно быть записано в одну строку с необходимым количеством круглых скобок, регулирующих порядок действий. Одна из
приятных особенностей пакета Mcd заключается в том, что арифметические выражения записываются в привычном для пользователя виде.
Например, выражение R=
1+ sin x +
-
x2
2
1
x2+1
должно быть записано
e + ln(1+|x|)
в QB и VBA строкой:
R = Sqr((1+Sin(x)+Sqr(1/(x^2+1)))/(Exp(-x^2/2)+Log(1+Abs(x)))),
тогда как в Mcd оно записывается в следующем, вполне привычном,
виде:
R:–
–
.
Здесь использованы имена встроенных функций, о которых будет сказано ниже, и операторы присваивания: "=" в QB и VBA, ":––" в Mcd.
Полезно отметить, что при вводе арифметических выражений в
Mcd следует ориентироваться на голубой подчеркивающий уголок,
отмечающий выражение, к которому применяется результат последуюшего ввода. Величина и положение этого уголка регулируется с помощью мыши и клавиши "пробел" (spacebar) консоли. Например, если
(1+x)2+x
необходимо вычислить (при х = 2) выражение 2x-1 , то необходимо
последовательно нажать на консоли клавиши: 1, +, x, "пробел" (для
выделения 1+х), "Shift"+6 (ввести степень), 2, "пробел" (для выделения
(1+х)2), +, х, "пробел" (выделить весь числитель), /, 2, *, х, -, 1
[,"пробел", "пробел", "пробел" – выделение всей дроби], = (на листе
появится результат 3.667).
13
1.2. ОСНОВНЫЕ ТИПЫ
Пользователь должен сообщить интерпретатору его программы,
какое место в памяти следует отводить используемым переменным и
константам и как этой памятью можно распорядиться. Поэтому перед
использованием этих объектов их нужно определить, указав для каждого его (базовый) тип с помощью инструкции:
Dim ‹имя переменной› As ‹тип›.
В одной строке можно определить несколько переменных:
Dim ‹имя1› As ‹тип1›, ‹имя2› As ‹тип2›, ‹имя3› As ‹тип3›, и т.д.
Константы определяются служеным словом Const, например,
Const pi As Double = 3.1415926535895.
Перечислим основные типы с указанием занимаемой памяти, допустимого диапазона, доступности в рассматриваемой среде (табл. 1).
Таблица 1
Тип
Диапазон
Байты
Логические
Целые
Длинные
Веществ.
Двойные
веществ.
С фикс.
точкой
Byte
Boolean
Integer
Long
Single
0…255
True-False
|x| ≤ 215-1
|x| ≤ 231
|x| ≤ 3.41038
|x| ≤ 1.710308
числа
Название
Double
Целая часть до 15
Currency знаков, дробная – до 4
Текстовые
~ 230 символов
String
В зависимости от
Произвольные Variant
содержания
Объекты
Object
Ссылки
память
в байтах QB
VBA Mcd
1
2
2
4
4
+
+
+
+
+
+
+
+
+
-
8
+
+
+
8
-
+
-
10+1 /s
b
+
+
+
≥ 16
-
+
-
4
-
+
-
Таким образом, Mcd по умолчанию использует лишь два типа
данных, остальные при необходимости получаются преобразованием
из этих двух с помощью встроенных функций.
1.2.1. Числа
Основным признаком действительного числа является наличие
десятичного разделителя – точки (не запятой, как в русскоязычной
литературе). В формате с плавающей точкой число может быть записано с масштабным множителем, указывающим степень десяти:
14
-3.92Е+4 есть запись числа -39200, запись
Const eps As Single = 1E-10
вводит константу ε = 0.0000000001. Константы (в отличие от переменных) не допускают изменения значений в программе.
При присваивании значений переменным типы данных преобразуются автоматически, когда не возникает конфликта памяти. Например, если переменная А определена типом Byte, В - типом Integer, C типом Single, D - типом Double, то после присваиваний (двоеточие является разделителем операторов внутри одной строки)
D = 3.14159265358937: C = D: B = C: A = B
получим значения 3 для А и В, 3.141593 для С (выполнено автоматическое округление при переходе к целому типу). Если вначале присвоим переменной D отрицательное значение, то на операторе А = В возникнет ошибка (переполнения).
Аналогично взаимодействуют типы Boolean и Integer. Значение
False логической переменной соответствует нулевому значению целой
переменной, тогда как True соответствует целому значению -1 (все
разряды заняты единицами). С другой стороны, если целочисленная
переменная имеет ненулевое значение, то ее логическое значение есть
True. Например, цепочка присваиваний
Dim B As Boolean, C As Integer, D As Long
C = -123: B = C: D = B
приводит к значениям True для В и -1 для D.
Приведем короткий список встроенных QB-функций, облегчающий конструирование алгебраических выражений (табл. 2).
Таблица 2
функция интерпретация
функция
ABS(x)
|x|
x MOD y
ATN(x)
arctg(x)
RND
COS(x)
EXP(x)
FIX(x)
cos(x)
x
e
SGN(x)
SIN(x)
SQR(x)
INT(x)
Отбрасывает дробную часть
Наибольшее целое, не
превосходящее х
LOG(x)
ln(x)
TAN(x)
интерпретация
Остаток от деления х
на у
Случайное число из
(0, 1)
Знак числа х
sin(x)
x
tg(x)
RANDOMIZE Старт для RND
15
VBA имеет более богатый набор встроенных функций. С полным
их списком можно познакомиться непосредственно в разрабатываемом приложении, введя в программе "vba." (не забудьте точку!).
Mcd позволяет часто используемые элементарные функции и алгебраические операции вводить из меню "Калькулятор" (см. рис. 2). С
полным набором встроенных функций можно ознакомиться в меню
"f(x)" (вставка функций) с раскрывающимся списком разделов и содержанием разделов (рис. 3).
Рис. 2
Рис. 3
Рассмотрим простой пример. Возьмем случайное число из промежутка (1, 5) и найдем произведение его целой и дробной частей. В
VBA задачу можно решить с помощью кода (с комментаниями):
Dim x As Single, a As Integer, b As Single, res As Single
Randomize Timer
'***запускаем прцесс рандомизации
x = 1 + 4*Rnd
'***случайное число
a = Int(x): b = x - a
'***выделение целой и дробной части
res = a * b
В Mcd код выглядит чуть иначе:
x :–– 1 + rnd(4) a :–– trunc(x) b :–– x - a res :–– a∙b = ‹результат›.
Кроме обычных действительных чисел Mcd допускает использование комплексных чисел с введением мнимой единицы.
1.2.2. Строки
Строкой назовем конкретное значение переменной или константы
типа String (заключенное в кавычки). Этот тип предполагает динамическое распределение памяти, поскольку произвольная строка может
содержать до 230 символов. Это несколько замедляет работу процессора. Можно определять строки фиксированной длины с помощью инструкции:
16
Dim ‹имя переменной› As String*‹количество символов›,
при этом, если переменной присваивается строка более длинная, чем
указано, то лишние символы отбрасываются (теряются), если строка
имеет меньший размер, то недостающие символы заменяются пробелами. Приведем неполный перечень функций и операторов обработки
строк в QB и VBA:
+ или "пробел"&"пробел" – последовательное сложение (объединение,
конкатенация) двух строк,
ASC(∙) возвращает значение кода одного символа в кодировке ASCII,
CHR(∙) возвращает символ с указанным ASCII-кодом,
HEX(∙) возвращает строку 16-чного представления числа,
INSTR([i],x,y) возвращает номер позиции, где впервые строка у входит
в состав строки х (выявление подстроки), начиная с позиции i (нумерация начинается с единицы),
LEFT(x,i) возвращает i левых символов строки х,
RIGHT(x,i) возвращает i правых символов строки х,
LEN(x) возвращает длину строки х (количество символов),
MID(x,i,j) возвращает подстроку в строке х длиной j символов, начиная с i-ой позиции (если аргумент j отсутствует, то выделяются
все символы строки х, начиная с i-го). Функция позволяет в заданное место одной строки вставлять другую строку (это единственный случай, когда имя функции может стоять слева от оператора присваивания).
FORMAT(∙), STR(∙) преобразуют число в текстовый формат (вторая
функция в отличие от первой добавляет пробел в начало строки),
STRING(n, z) возвращает строку из n символов z (или символов с
ASCII-кодом z).
TRIM(∙) убирает начальные и конечные пробелы в строке.
UCASE(∙), LCASE(∙) преобразуют элементы строки к верхнему и нижнему регистрам.
VAL(x) преобразует строку х в соответствующий числовой формат
(если это невозможно, функция возвращает ноль).
Mcd использует другие названия функций для сходных операций:
concat(∙) возвращает конкатенацию (объединение) строк-аргументов,
IsString(S) возвращает 1, если S – строка, иначе возвращает 0,
num2str(∙) переводит число в текстовый формат,
strlen(∙) возвращает длину (количество символов) строки,
str2num(∙) преобразует текстовое выражение в числовой формат,
str2vec(∙) преобразует текстовое выражение в последовательность
ASCII-кодов,
17
substr(S,m,n) действует, как Mid(S,m,n) VBA (но нумерация по умолчанию начинается с нуля),
vec2str(v) возвращает строку символов с ASCII-кодами v.
Преобразование строк полезно использовать для подготовки данных к выводу на печать или для сохранения в текстовом файле, также
в тех случаях, когда нужно обрабатывать часть числа.
Пример. Пусть дано целое четырехзначное число N. Требуется
переставить в нем циклически цифры четыре раза, все полученные числа сложить и результат поделить на сумму цифр числа N.
Рассмотрим решение задачи в VBA в терминах целых чисел. Определим четыре целых числа для результатов перестановок цифр и для
суммы цифр числа N:
Dim N1 As Integer, N2 As Integer, N3 As Integer, S As Integer
Dim k As Integer, res As Integer.
Сумму цифр получим последовательностью операций:
k = N: S = k Mod 10: k = k \10 '***целочисленное деление
S = S + k Mod 10: k = k \ 10: S = S + k Mod 10 + k \ 10.
Выполним перестановку цифр:
N1 = (N Mod 10)*1000 + N \ 10: N2 = (N1 Mod 10)*1000 + N1 \ 10
N3 = (N2 Mod 10)*1000 + N2 \ 10.
Теперь получим результат:
res = (N + N1 + N2 + N3) \ S.
В Mcd те же операции из-за отсутствия целого типа выглядят
несколько иначе (функция trunc возвращает целую часть числа):
k :–– n s :–– mod(k, 10) k :–– trunc(0.1∙k) s :–– s + mod(k, 10)
k :–– trunc(0.1∙k) s :–– s + mod(k, 10) + trunc(0.1∙k)
n1 :–
– 1000∙mod(n, 10) + trunc(0.1∙n)
n2 :–
– 1000∙mod(n1, 10) + trunc(0.1∙n1)
n+n1+n2+n3
n3 :–
– 1000∙mod(n2, 10) + trunc(0.1∙n2) res :––
s
.
Используя преобразования типов число ⇔ строка, можно решение организовать по-другому.
В VBA: введем дополнительно четыре текстовые переменные
Dim t As String, t1 As String, t2 As String, t3 As String.
Далее,
t = Format(N)
k = Val(Left(t,1)) + Val(Mid(t,2,1)) + Val(Mid(t,3,1)) + Val(Right(t,1))
t1 = Right(t,1) & Left(t,3): t2 = Right(t1,1) & Left(t1,3)
18
t3 = Right(t2,1) & Left(t2,3)
res = (Val(t) + Val(t1) + Val(t2) + Val(t3)) \ k .
В Mcd выглядит все совершенно аналогично, если в соответствии
с предыдущим всюду функцию Val заменить на str2num, Left(), Mid()
и Right() заменить функцией substr() с соответствующими параметрами (учитывая индексацию с нуля).
Приведем таблицу кодов основных символов ASCII.
Таблица 3. Основная таблица кодов
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
♦
23
24
tab 25
26
♂ 27
28
29
♫ 30 31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
!
"
#
$
%
&
'
(
)
*
+
,
.
/
0
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
1
2
3
4
5
6
7
8
9
:
;
<
=
>
?
@
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
Q
R
S
T
U
V
W
X
Y
Z
[
\
]
^
_
`
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
p
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
q
r
s
t
u
v
w
x
y
z
{
|
}
~
•
Таблица 4. Дополнительная (расширенная) таблица кодов
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
Ђ
Ѓ
‚
ѓ
„
…
†
‡
€
‰
Љ
‹
Њ
Ќ
Ћ
Џ
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
ђ
‘
’
“
”
•
–
—
˜
™
љ
›
њ
ќ
ћ
џ
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
Ў 177
ў 178
Ј 179
¤ 180
Ґ 181
¦ 182
§ 183
Ё 184
© 185
Є 186
« 187
¬ 188
­ 189
® 190
Ї 191
°
±
І
і
ґ
µ
¶
∙
ё
№
є
»
ј
Ѕ
ѕ
ї
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
а
б
в
г
д
е
ж
з
и
й
к
л
м
н
о
п
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
р
с
т
у
ф
х
ц
ч
ш
щ
ъ
ы
ь
э
ю
я
19
Коды 1, 12, 31 – служебные, 9 – код табуляции, коды 10 и 13 вызывают при выводе переход на другую строку (их полезно использовать
при выводе информации в несколько строк, принудительный "возврат
каретки"), 32 – код "пробела", остальные – коды псевдографики, цифры, латинница, арифметические знаки, скобки и коды некоторых
клавиш консоли. Дополнительная таблица содержит знаки кириллицы
и часто используемые типографские знаки.
С типами Variant и Object приходится сталкиваться в отдельных
особых случаях. Эти типы будут оговорены в подходящих для этого
местах. По поводу типа Variant полезно отметить следующее: если
объект не определен соответствующей инструкцией Dim, то по умолчанию он считается принадлежащим типу Variant. Это некорректно с
точки зрения программирования и в конфликтных ситуациях может
приводить к скрытым, трудно определяемым ошибкам. Поэтому все
переменные, константы и другие объекты должны быть определены с
указанием их типов.
1.3. ОПЕРАТОРЫ ВВОДА И ВЫВОДА
Выше уже отмечена тенденция отделять пользователя от непосредственного участия в управлении компьютером. В Mcd все вычисления проводятся автоматически непосредственно на рабочем листе,
поэтому там отпадает необходимость в специальных операторах ввода-вывода (за исключением операций с файлами, но об этом позже).
В QB (при прямой работе в DOS – дисковой операционной системе) ввод с клавиатуры осуществлялся с помощью оператора INPUT,
после которого следовал список переменных ввода. Этот же оператор
использовался при вводе информации из файла (см. ниже). Оператор
вывода PRINT, также со списком переменных (объектов вывода), использовался как для непосредственного вывода на экран дисплея, так и
для вывода в файл.
VBA сохранил эти операторы, в основном для работы с файлами.
В различных приложениях ввод информации организуется специальным для этого приложения способом (например, в таблицы, надписи,
ячейки диалоговых окон, и т.д., о некоторых из них будет идти речь
позже). В случае простого обмена (диалога) можно воспользоваться
специальной функцией ввода InputBox() с необязательными аргументами Prompt – текст подсказки, Title – текст заголовка, Default – вводимое по умолчанию значение, и др. Функция вводит информацию с
клавиатуры только в текстовом виде. Если необходимо ввести число, к
функции следует применить функцию-преобразователь Val.
Ситуация с выводом в сущности такая же: каждое приложение
имеет свои специфические формы вывода. Общим является диалоговое окно, вызываемое оператором MsgBox. Поскольку это оператор, а
20
не функция, т.е. он должен производить действие, а не возвращать значение, его (необязательные) аргументы указываются далее без скобок:
Prompt – выводимый текст, дополнительные кнопки на диалоговой
панели, Title – заголовок, и др. Так же, как и при вводе, если необходимо вывести в диалоговое окно числовое значение, то его полезно предварительно преобразовать в строковый формат.
Пример. Организуем диалог с компьютером (Комп – Студ):
Комп: "Доброе утро!"
Студ: "Доброе утро!"
Комп: "Как Ваше имя?"
Студ: "Сергей"
Комп: "Привет, Сергей! Сколько тебе лет?"
Студ: "19"
Комп: "Ну-у, тебе еще жить, да жить. А я, вот, с прошлого века..."
Студ: "Мне очень жаль. Сколько же тебе лет?"
Комп: "Да побольше, чем 20."
в виде кода:
Sub Dialog()
Dim txt as string, n As Byte
txt = InputBox("Доброе утро!", "", "")
'***здоровается
txt = InputBox("Как Ваше имя?", "", "") '***студент вводит имя
'***прибавляется имя к приветствию, переход на новую строку
n = Val(InputBox("Привет, " & txt & "!" & Chr(13) & _
"Сколько тебе лет?", "","0"))
'***ввод возраста
txt = InputBox("Ну-у, тебе еще жить, да жить." & Сhr(13) & _
"А я, вот, с прошлого века...", "", "")
' ***вводится реакция студента
MsgBox "Да побольше, чем " & Format(20), vbExclamation, ""
End Sub .
Здесь использован комментарий '***... и способ непрерывного продолжения строки на следующей: "пробел" и знак подчеркивания,
константа vbExclamation добавляет в диалоговое окно восклицательный знак.
Во многих приложениях (например, Excel, Word, и др.) пользователь может вводить специальную форму, которая является контейнером для различных элементов управления и дополнительных окон
ввода и вывода информации. Visual Basic, как самостоятельный язык
для создания приложений, имеет возможность непосредственного
текстового вывода в форму с помощью оператора Form.Print. Форма
при этом позволяет изменять тип, размер, цвет шрифта, стартовую позицию печати, выводить некоторые графические элементы, так что она
вполне заменяет (на уровне окон) взаимодействие QB – экран.
21
1.4. ФУНКЦИИ И ПОДПРОГРАММЫ
Функция – это отдельная самостоятельная программа, возвращающая результат в виде значения определенного типа. Поэтому имя
функции может содержаться в любом арифмерическом операторе и
операторе присваивания наравне с любыми другими переменными и
константами. В VBA функция определяется заголовком
Function ‹имя›([аргументы]) As ‹возвращаемый тип›,
после чего следует программный код – тело функции, и обязательная
завершающая часть
End Function.
Таким образом, рабочая часть (тело функции) должна быть заключена
между "операторными скобками" Function - End Function. Аргументы
функции (если они есть) должны быть указаны вместе со своим типом
(в противном случае они будут иметь тип Variant), тип возвращаемого
значения тоже должен быть указан. В теле функции (т.е. в ее программной части) должно быть хоть одно присваивание переменной с именем функции, иначе она будет возвращать нулевое значение.
При описании функции имена аргументов – формальные, при использовании функции они заменяются фактическими. Здесь возможны
два способа замены формальных параметров фактическими. Первый –
вместо формальных параметров подставляются копии значений фактических параметров, так что любые их изменения внутри функции не
отражаются на фактических параметрах. Второй – формальным параметрам ставится в соответствие ссылка на фактические параметры, так
что изменение значений параметров внутри функции изменит значения и фактических параметров. Поэтому полезно в первом случае указывать при определении функции параметры со служебными словами
ByVal (по значению), во втором случае – ByRef (по ссылке). По
умолчанию (если явно не указано) имеется в виду второй способ –
ссылка на фактические параметры (ByRef).
Пример. Как известно, наибольшее значение чисел х и у можно
вычислить по формуле: max(x, y) = 0.5∙(x + y + |x - y|). Рассмотрим следующий код:
Dim a As Single, b As Single
'*** определение функции
Function Max(x As Single, y As Single) As Single
y = 0.5*(x + y + Abs(x - y)) '*** изменение второго аргумента
Max = y
End Function
'*** ввод чисел а и b
а = Val(InputBox("введите значение а", "", 0))
22
b = Val(InputBox("введите значение b", "", 0))
'*** вывод Max(a, b), a, b
MsgBox "max=" & Format(Max(a, b)) & ", a=" & Format(a) _
& ", b=" & Format(b) .
Введя a = 15, b = 7, получим результат:
max=15, a=15, b=15.
Значение b изменилось, так как оно было введено по ссылке (умолчание). Если бы в определении функции явно сослались на значение аргумента
Function Max(ByVal x As Single, ByVal y As Single) As Single,
то получили бы результат: max=15, a=15, b=7 (заметим, что в действительности в теле функции можно было бы сразу выполнить присваивание Max = 0.5*(x + y + Abs(x - y)), приведенный вариант имеет чисто
демонстрационное значение).
Переменные, определенные вне функции, являются определенными и внутри функции (если они не переопределены), определенные внутри функции оказываются недоступны вне ее (локальное определение). Здесь применяется правило наследования: "что снаружи, то
и внутри", но не наоборот. Если желательно сделать переменные (или
функции) доступными всюду, то их необходимо сделать как можно
более "внешними" и вместо инструкции Dim использовать инструкцию Public. Принудительный выход из функции – Exit Function.
Mcd не требует определения типов (их всего два и они легко различаются: строка всегда заключена в кавычки). Кроме того, функции
могут возвращать любой вычислимый объект, будь то число, вектор,
матрица, и т.д. Имени функции не нужно присваивать возвращаемое
выражение, оно обычно указывается самостоятельно в конце блока определения функции, либо после служебного слова "return". Параметры функции вводятся (по умолчанию) как значения фактических параметров (т.е. ByVal), а сама функция определяется с помощью оператора присваивания. Функцию последнего примера в Mcd можно определить совсем просто:
Max(x,y) :–– 0.5∙(x + y + |x - y|).
Подпрограмма не допускает присваивания ее имени какого-либо
значения, она ничего не возвращают, она является методом реализации какого-то процесса. В отличие от функции она определяется "операторными скобками" Sub ‹имя› ([параметры]) ... End Sub.
Запускать подпрограмму самостоятельно можно так же, как любую программу (Run, F5, и т.д.). Внутри другой программы ее можно
вызвать, указав ее имя и параметры (в VBA – без скобок). Подпрограммы без параметров (но со скобками) иногда называются макросами.
23
Принудительный выход из подпрограммы – инструкция Exit Sub.
Подпрограммы, как правило, изменяют значения своих параметров или внешних переменных, что, собственно, и является результатом их работы. В Mcd большинство подпрограмм реализованы в виде
функций, поэтому там нет необходимости в таком разделении свойств.
1.5. РАЗВЕТВЛЕНИЕ И АЛЬТЕРНАТИВА
1.5.1. Безусловный выбор
Обычное разветвление программы осуществляется с помощью
оператора GoTo ‹метка›, либо оператором перехода с выбором:
On ‹арифм. выражение› GoTo ‹метка1›, ‹метка2›, ...
При этом арифметическое выражение округляется до целого значения
n и выполняется переход к n-й метке списка. Например, найти все корни квадратного уравнения можно было бы программой:
Sub Roots(a As single, b As Single, c As single)
Dim i As Integer, d As Single
d = b*b – 4*a*c: i = 2 + Sgn(d)
On i GoTo Zero, One, Two
Ex:
MsgBox "Задача решена": End
Zero: MsgBox "Действительных корней нет": End
One: MsgBox "Один корень х=" & Format(-0.5*b/a): GoTo Ex
Two: d = Sqr(d)
MsgBox "Два корня: " & Format(0.5*(d-b)/a) & _
"и " & Format(-0.5*(d+b)/a): GoTo Ex
End Sub .
Полезно отметить, что безусловный переход не популярен в программировании, это своего рода анахронизм. В Mcd он вообще отсутствует.
1.5.2. Условный выбор
В VBA используются три вида операторов.
1) Простое условие реализуется оператором
If ‹условие› Then ‹оператор1›.
Оператор1 выполняется, если указанное условие удовлетворено, в
противном случае программа переходит к выполнению следующей за
условным оператором строки.
2) Условие с альтернативой реализуется оператором
If ‹условие› Then ‹оператор1› Else ‹оператор2›,
24
при этом оператор1 и (или) оператор2 сами могут быть условными
операторами. Здесь условие должно быть логическим выражением,
возможно с использованием логических связок: Or = "или", And = "и",
Xor = "разделенное или", Not = "не" в соответствии со следующей
таблицей истинности (см. табл. 5):
Таблица 5
x
True
True
False
False
y
True
False
True
False
x Or y
True
True
True
False
x Xor y
False
True
True
False
x And y
True
False
False
False
Любые другие логические формулы получаются из приведенных в
таблице. При логических сравнениях используются символы: =, <, >.
Сравнения ≤, ≥, ≠ записываются соответственно как <=, >=, <>.
В качестве условия может быть использована также функция
MsgBox с диалоговым окном, содержащим кнопки выбора: "Yes",
"No", "Cancel", и другие. Например, код:
If MsgBox("Продолжить вычисления?", vbYesNo, "АЛЬТЕРНАТИВА") _
= vbNo Then End
заканчивает работу программы, если на панели окна выбрана кнопка
"No", в противном случае работа продолжается.
Пусть требуется при заданных значениях х и у вычислить
0 при x = y,
выражение
f
1 + x + y
 2 6 при х≠ у и х+2 ≠ у,
=  1+ 2
x-y
1 при y = x+ 2,
-1 в ост. случаях.
Запишем условный
оператор (присвоение должно быть при каждом условии):
If x = y Then f = 0 Else If (x<>y) And (y<>x+2) Then _
f = (1 + x/2 + y/6) / (1 + 2/(x – y)) Else If y = x+2 Then f = 1 _
Else f = -1
(внимание! Условный оператор должен быть записан в одной строке,
здесь использовано продолжение строки: пробел + подчеркивание).
В Mcd есть специальная функция, возвращающая значение с
условием (ее можно найти в общем списке функций, см рис. 3) вида
if(▪, ▪, ▪), в которой на первом месте стоит условие, на втором –
арифметический оператор1, на третьем – арифметический оператор2.
Функция допускает многократные вложения, так, предыдущий пример
можно записать в Mcd следующим образом:
25
.
Как показывает пример, Mcd использует иные обозначения для записи логических условий: неравенство записывается привычным знаком,
сравнение записыается "утолщенным" знаком
равенства, связка And записывается как "∧",
Or – как "∨", Xor – как "⊕", Not – как "−"
(см. рис. 4).
|
3) Условный блок записывается в форме:
If ‹условие› Then
‹блок операторов›
Else
‹блок операторов›
End If.
Рис. 4
При этом блок Else (который может отсутствовать, если нет альтернативы) может сам обрабатывать условие в виде блока
ElseIf ‹условие› Then
‹блок операторов›.
В этом случае (в отличие от простого или альтернативного условия)
каждый элемент условного оператора (т.е. If – Then, ElseIf - Then,
Else, End If) должен быть записан в отдельной строке.
В Mcd блок операторов всегда вводится с помощью вертикальной
черты, и в каждой строке записывается по одному оператору.
Вертикальную черту, как и другие операторы
программирования, можно ввести из меню программирования, щелкнув мышкой по иконке
и выбрав из раскрывающегося меню (рис. 5)
необходимый оператор. Здесь "Add Line" –
вставка вертикальной черты, "If" – условный
оператор (исполняемая часть стоит перед If,
условие – после), альтернативе Else соответРис. 5
ствует оператор "otherwise". Присваивание в
программах и блоках всегда записывается левой стрелкой. Оператор
"return" возвращает указанное значение.
26
Разберем в качестве примера рассмотренную выше задачу (см. п.
1.5.1): выяснить все возможные случаи наличия или отсутствия действительных корней квадратного трехчлена ax2 + bx + c в зависимости
от значений его коэффициентов. Здесь возможно следующее.
1. Коэффициент а = 0.
2. Если при этом и b = 0, то приходим к равенству с = 0, которое
невозможно при с≠0
3. Но если и с = 0, то трехчлен тождественно равен нулю
при любом значении аргумента х.
4. Если же b≠0 (при а = 0), то решение очевидно: единственный
действительный корень x = - c , конец задачи.
b
5. Если а≠0, то можно вычислить дискриминант d = b2 - 4ac.
6. Если он отрицательный, то действительных корней нет,
задача закончена.
7. В противном случае вычисляем корень из дискриминанта,
полагая d :–– d.
8. Если значение d мало по абсолютной величине, то его
можно считать равным нулю и указать действительный
b
корень x = - , решение закончено.
2a
-b-d
d-b
9. Иначе указываем два корня 2a и 2a . Анализ закончен.
Упражнение. Постройте блок-схему приведенного анализа.
Здесь почти каждое условие имеет свою альтернативу If – Then –
Else и обработка некоторых условий требует больше одного оператора. Поэтому код программы следует организовать в виде условного
блока. В VBA реализуем его в виде подпрограммы:
Sub TrinomRoots(a As Single, b As single, c As Single)
Dim d As Single, x1 As Single, x2 As Single
Const eps As Single = 1E-6 '*** константа для разделения корней
If a = 0 Then
If b = 0 Then
If c = 0 Then MsgBox "корень – любое число" _
Else MsgBox "корней нет"
Else
MsgBox "корень= " & Format(-c/b)
End If
Else
d = b^2 – 4*a*c
If d < 0 Then
MsgBox "действительных корней нет"
Else
d = Sqr(d)
If d < eps Then
27
MsgBox "один корень= " & Format(-b/(2*a))
Else
x1 = -(b + d)/(2*a): x2 = (d – b)/(2*a)
MsgBox "два корня: " & Format(x1) & "и " & Format(x2)
End If
End If
End If
End Sub .
Отметьте, пожалуйста, для себя стиль записи программ: начало и
конец соответствующего блока следует записывать с одинаковых позиций в строке (по вертикали в этой позиции больше ничего не должно
быть), вложенные блоки сдвигаются вправо (например, с помощью
клавиши "Tab" консоли). Это делает структуру более понятной, в ней
легко найти возможные ошибки и логические несоответствия. Полезно
с самого начала приучать себя к "культуре" записи кодов.
В Mcd пример можно реализовать в виде функции:
TrinomRoots(a, b, c) :––
ε ← 0.000001
if a = 0
if b = 0
return "любое число" if c = 0
return "нет корней" otherwise
-c
return
otherwise
b
otherwise
d ← b2 – 4∙a∙c
return "действительных корней нет" if d < 0
otherwise
-b
return
if d < ε
2∙a
-b-d
2∙a
return d-b otherwise
2∙a






Записав теперь TrinomRoots(3, 2, -1) = 2.333, получим значения корней трехчлена 3х2 + 2х - 1. Для вывода значений обоих корней (последняя строка функции) можно, щелкнув мышкой по иконке
меню,
вызвать меню матричных
операторов (рис. 6), щелчок
по иконке матрицы вызывает меню вставки матрицы,
где можно выбрать нужный
размер (в нашем случае две
строки и один столбец). Это
Рис. 6
можно сделать и с клавиатуры, набрав Ctr +"M".
-3
28
Сравнивая эти две программы, легко заметить почти полную их
идентичность: конструкция If – Then – Else VBA однозначно соответствует паре if – otherwise Mcd, MsgBox ⇒ return, а блок операторов наглядно представлен вертикальной чертой. Кроме того, если операторы вводить из соответствующего меню, то они вставляются вместе с указанием мест (в виде черных квадратиков) для помещения объектов действия. Например, условный оператор вводится как ▪ if ▪ - в
место левого квадратика вводится оператор, в место правого – условие.
Если необходимо построить условный блок, то в позицию левого
квадратика вводится "Add Line". Аналогично, альтернатива вводится
как ▪ otherwise, вывод – как return ▪, и т.д., так что все становится достаточно прозрачным.
1.5.3. Альтернативный выбор
Это – выбор по значению. Он реализуется блоком Select Case, который имеет структуру:
Select Case ‹идентификатор›
Case ‹выражение›
'***конкретное значение
‹блок операторов›
Case ‹выр.›, ‹выр.› Is ‹сравнение› ‹выражение› '***сравнение
‹блок операторов›
Case ‹выр.› To ‹выр.›
'***перечисление
‹блок операторов›
Case Else
'***все остальное
End Select
(Select Case – End Select – своеобразные "операторные скобки").
Этот оператор, очевидно, имеет более широкие возможности, чем условный блок, и записывается короче, хотя, конечно же, можно вполне
обойтись и без него – в Mcd этот оператор отсутствует.
Пусть, например, необходимо знать, есть ли в предлагаемом тексте цифры, буквы латинского алфавита, буквы кириллицы. Это можно
сделать с помощью программы:
Sub Analysis(txt As String)
Dim n As Integer, i As Integer, s As String*1, Cyf As Byte, Lat As Byte
Dim Cir As Byte, Rest As Integer
n = Len(txt): txt = LCase(txt)
'***перевод в нижний регистр
Start: i = i + 1: t = Mid(txt, i, 1)
Select Case t
Case "0" To "9": Cyf = Cyf + 1 '***считаем цифры
Case "a" To "z": Lat = Lat + 1 '***считаем буквы латинницы
Case "а" To "я": Cir = Cir + 1 '***считаем буквы кириллицы
Case Else: Rest = Rest + 1
'***считаем все остальное
End select
If i < n Then GoTo Start
29
MsgBox "В данном тексте:" & Chr(13) & _ '***переход на новую строку
"цифр -" & Format(Cyf) & Chr(13) & _
"латинских букв -" & Format(Lat) & Chr(13) & _
"букв кириллицы -" & Format(Cir) & Chr(13) & _
"прочих символов -" & Format(Rest)
End Sub .
Участок программы Start – GoTo Start лучше выполнять с помощью конструкции цикла (см. следующий пункт).
1.6. ЦИКЛЫ
Циклы предназначены для программирования регулярных повторяющихся действий. Они значительно упрощают и сокращают рутинную работу.
Цикл
заголовок
цикла
конец
цикла
тело цикла
группа операторов
Заголовок цикла и конец цикла образуют своеобразные "операторные
скобки", которые, собственно, и определяют тип цикла. В VBA используются, в основном, следующие типы циклов.
1) Безусловный цикл: заголовок
DO
конец
LOOP
2) Цикл пересчета имеет сложный заголовок.
Заголовок:
стартовое
конечное
For ‹счетчик› =  значение  To  значение 





шаг изменения
Step 

счетчика 


Конец:
NEXT
3) Цикл с предусловием
заголовок While ‹ усл. › Do While ‹ усл. ›
конец
Wend
Loop
Do
Loop While ‹ усл. ›
4) Цикл с постусловием
заголовок
Do Until ‹ усл.›
Do
30
конец
Loop
Loop Until ‹ усл. ›
Выход из цикла можно осуществить с помощью оператора Exit
с указателем типа цикла, т.е. Exit Do или Exit For.
В Mcd применяются лишь два типа циклов: цикл пересчета For ...
(без возможности выбора шага) и цикл с предусловием While ..., остальное – дело пользователя и его изворотливости. Во многих простых
задачах можно обойтись каким-нибудь одним типом "на все случаи
жизни", смысл и логика задачи, тем не менее, определяют наиболее
подходящий тип.
Пример 1. Рассмотрим в качестве примера следующую простую
задачу: найти наименьшее натуральное значение аргумента х, синус
которого по абсолютной величине не превосходит 0.0001, т.е. найти
min{x∈ℕ: |sin(x)| < 0.0001}. Здесь достаточно перебирать последовательно все натуральные числа и остановить перебор, когда выполнится требуемое условие. Для этой цели подойдет любой тип цикла. Посмотрим, как это будет выглядеть в VBA.
Безусловный цикл:
Dim n As Integer
Do: n = n + 1
If Abs(Sin(n)) < 0.0001 Then Exit Do
Loop
Цикл пересчета:
Dim n As Long
For n = 1 To 1000000000
If Abs(Sin(n)) < 0.0001 Then Exit For
Next
Цикл с предусловием:
Dim n As integer
n=1
While Abs(Sin(n)) >= 0.0001
n=n+1
Wend
или
Do While Abs(Sin(n)) >= 0.0001
n=n+1
Loop
Цикл с постусловием:
Dim n As Integer
Do: n = n + 1
Loop Until Abs(Sin(n)) < 0.0001
Необходимо заметить, что цикл пересчета не выполняется, когда текущее значение счетчика превосходит его конечное значение
(при прямом проходе). В циклах с предусловием сначала проверяется
условие, затем решается вопрос о необходимости выполнения цикла.
Циклы с постусловием всегда выполняются хоть один раз.
31
В Mcd этот пример целесообразно решить в виде кода:
n←1
= 355
while |sin(n)| ≥ 0.0001
n←n+1
n
Здесь нет необходимости создавать функцию (для одноразового вычисления). Приведенный блок содержит в конце одну переменную, n,
значение которой необходимо сообщить в результате вычисления
(знак равенства после блока "высвечивает" значение n = 355), можно
было бы использовать также оператор return n.
Пример 2. Пусть требуется вычислить значение непрерывной
1
дроби d = 2 +
, образуемой двумя последовательностями
2
3+
4 + ..
. 9
+ 11
чисел: {2, 3, 4, ..., 11} и {1, 2, 3, ..., 9}. Вычисление следует проводить
"с хвоста": взять число 11, затем 9 поделить на 11 и прибавить 10,
затем 8 поделить на результат и прибавить 9, и т.д. Таким образом,
алгоритм вычисления выстраивается в следующий цикл пересчета в
обратном порядке (т.е. с шагом -1):
Dim n As Integer, d As Single
d = 11
For n = 10 To 2 Step -1
d = n + (n - 1) / d
Next
В Mcd цикл пересчета вводится из меню (см. рис. 5) в виде
for
▪
▪ ∈ ▪ , где в первой строке указаны места для счетчика и диапа-
зона его изменения, нижний квадратик – для тела цикла (в это место
можно вставить вертикальную черту –"Add Line"). Диапазон изменения счетчика можно указать явным перечислением его значений
или с помощью операции "ранжирования", используя оператор ".."
(клавиша ";" на латинской клавиатуре или меню матричных операций,
см. рис 6 слева)
d ← 11
for n ∈ 10..2
n-1
d←n+
d
d
= 2.291
32
В циклах пересчета Mcd прямой и обратный ход записываются одинаково. Это таит в себе некоторую опасность: в Mcd цикл пересчета выполняется всегда.
Пример 3. Построим функцию, которая каждому натуральному n
3
(k-1) 
k-1
ставит в соответствие min {ak = k + 1 + sin k+1 , ak > 0}. Очевидно,
1≤k≤n
все ak < 2, так что с самого начала значения чисел нужно сравнивать с
числом 2. В VBA код будет иметь вид:
Function Choice(n As Integer) As Double
Dim min As Double, a As Double, r As Double, k As Integer
min = 2
For k = 2 To n: r = (k – 1) / (k + 1)
a = r + sin(r * (k – 1)^2)
If a > 0 And a < min Then min = a
Next: Choice = min
End Function .
В Mcd:
Choice(n) : = min ← 2
for k ∈ 2 .. n
k-1
r←
k+1
a ← k + sin(r∙(k - 1)2)
min ← a if a > 0 ∧ a < min
min
Циклы с условием позволяют организовать паузу заданной длительности, используя функцию Timer, возвращающую текущее время
процессора в секундах. Например, паузу в пять секунд можно создать,
вставив в программу код (цикл с пустым телом):
t = Timer + 5: While Timer <t: Wend.
Пример 4. Рассмотрим более сложную задачу. Известно, что значение тангенса угла х (угол дан в радианах) можно с восемью верными
(x2 - 105)∙x2 + 945
знаками вычислить по простой формуле: tg(x) = x∙
,
(15∙x2 - 420)∙x2 + 945
π
π
если |x| < 4 . С другой стороны, угол всегда можно изменить на 4 , ис1+ tg(x)
π
пользуя равенство tg(x + 4) =
. Построим алгоритм вычисле1- tg(x)
ния тангенса любого угла, используя приведенные формулы. Очевидно, знак угла не играет роли. Нужно определить, сколько раз содерπ
жится число 4 в заданном угле и найти оставшуюся часть. Если оставшаяся часть близка к нулю (с заданной точностью, будем называть это
33
"вырождением"), то tg(x) может принимать значения 0, ±1 или ∞, в
противном случае можно воспользоваться приведенными формулами
π
столько раз, сколько раз 4 содержится в аргументе х. Алгоритм можно
оформить в виде функции Tg(x). Окончательно имеем:
Sub Tg(x As Single) As Single
Dim p4 As Single, y As Single, z As Single, t As Single, k As Integer, n As Byte
Const pi As Double = 3.141592653586
'***ввод константы π
Const eps As Double = 0.0000000001
'***константа ε
p4 = pi / 4: y = Abs(x): k = Int(y / p4): t = y - k * p4 '***выделение остатка
If Abs(t) < eps Then
'***анализ на вырождение
n = k Mod 4
Select Case n
Case 0: t = 0
Case 2: t = 1E+35
Case Else: t = (-1) ^ n * Sgn(x)
End Select
Else
'***невырожденный случай, используем формулы
z = t ^ 2: t = t * ((z - 105) * z + 945) / ((15 * z - 420) * z + 945)
For n = 1 To k
t = (1 + t) / (1 - t)
'***пересчет тангенса
Next
End If: Tg = t*Sgn(x)
'***учет знака аргумента
End Sub .
В Mcd имеется встроенная константа π, есть также символ "∞",
который обозначает наибольшее действительное число, используемое
в вычислениях. Кроме того, конструкцию "Select Case ... End Select"
можно реализовать многократным вложением функции if. Наконец,
поскольку вырожденный и регулярный случай различаются по-существу, можно в первом случае просто прервать дальнейшие вычисления.
Tg(x) : =
ε ← 10-10
π
p4 ←
4
y ← |x|
k ← trunc
y
p4
t ← y – k∙p4
if |t| < ε
n ← mod(k, 4)
n
return if [n = 2, ∞, if [n = 0, 0, (-1) ∙sign(x)]]
break
z ← t2
(z - 105)∙z + 945 
t←t
(15∙z - 420)∙z + 945
for n ∈ 1 .. k
1+t
t←
1-t
t∙sign(x)
34
(функция sign(∙) возвращает знак аргумента).
Пример 5. Рассмотрим алгоритм перевода десятичного числа в
число системы счисления с основанием q. Если q > 10, то недостающие цифры заменяются буквами латинского алфавита (в 16-чной системе счисления цифры суть 0, 1, ..., 9, A, B, C, D, E, F). Так как латинский алфавит содержит 26 букв, то в нашем примере q ≤ 36. Если десятичное число N натуральное, то соответствующее его q-представление получается из цепочки равенств
N = N1q + R1 (N1 – частное от деления N на q, R1 – остаток)
= (N2q + R2)q + R1 = ... + R3q2 + R2q + R1,
поэтому достаточно делить последовательно число N на q до нуля и
выписывать все остатки. Если положительное число N < 1, то цифры
Rk нового представления получаются как Rk = [Nk-1q], Nk = {Nk-1q} – целая и дробная часть произведения Nk-1q, N0 = N. Знак числа можно
учесть при выводе результата. Построим функцию, возвращающую
представление десятичного числа а в системе счисления с основанием
q с числом знаков дробной части не более десяти. Полезно в функциях
предусмотреть "нештатную" ситуацию. Будем считать выбор основания q "незаконным", если q < 2 или q > 36. В Mcd при отсутствии
определения типов следует еще позаботиться о целочисленном q. В
VBA такая необходимость отсутствует. Результат должен быть текстовым выражением.
Function Transform(ByVal a As Double, q As Byte) As String
Dim u As Long, v As Double, z As integer, r A Byte, s As String
Const B As String = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
If q < 2 Or q > 36 Then
MsgBox "Illegal Basis", vbExclamation, "ERROR": Exit Function
End If
If a = 0 Then
Transform = "0": Exit Function
End If
z = Sgn(a): a = Abs(a): u = Int(a): v = a – u '***отделение целой и дробной частей
While u > 0
'***преобразование целой части
r = u Mod q
'***получение остатка
u=u\q
s = s & Mid(B, r+1, 1)
'***добавление очередного знака
Wend
If v > 0 Then
'***преобразование дробной части
s = s & "."
For u = 1 to 10
v = v*q: r = Int(v): v = v - r: s = s & Mid(B, r+1, 1)
Next
End If
If z < 0 Then s = "-" & s
Transform = s
End Function .
35
Соответствующий Mcd-вариант функции имеет вид:
Transform(a, q) : = B ←"0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
if q < 2 ∨ q > 36 ∨ q ≠ trunc(q)
return "Illegal arguments"
break
return "0" if a = 0
otherwise
z ← sign(a)
a ← |a|
u ← trunc(a)
v←a–u
s ← ""
while u > 0
r ← mod(u, q)
u
u ← trunc  
q
s ← concat(substr(B, r, 1), s)
if v > 0
s ← concat(s, ".")
for u∈0 .. 9
v ← v∙q
r ← trunc(v)
v←v–r
s ← concat(s, substr(B, r, 1))
s ← concat("-", s) if z < 0
s
Циклы, как и условные операторы, легко вкладываются друг в
друга, причем вложенные циклы должны различаться параметрами и
во внутреннем цикле (равно и в теле цикла) не следует менять параметры (внешнего) цикла.
Пример 6. Есть следующе "простое" правило сокращения простых дробей – зачеркивание одинаковых цифр числителя и знамена20
∖
∖
64 4
= 2,
= = 4 (все правильно!). Найти все дроби с
10
∖
1∖
6 1
двузначными числителями и знаменателями, для которых это правило
применимо (исключая равные числители и знаменатели, а также сокращение на ноль). Задачу легко решить с помощью VBA-кода:
теля, например,
Dim m As Byte, n As Byte, a As Byte, b As Byte, c As Byte, d As Byte, q As Single
For m = 10 To 99
For n = m + 1 To 99
a = m \ 10: b = m Mod 10
c = n \ 10: d = n Mod 10
If b <> 0 Then
If a = c Then
q=d/b
ElseIf a = d Then
q=c/b
36
ElseIf b = c Then
q=d/a
ElseIf b = d Then
q=c/a
Else
q=0
End If
End If
If q = n / m Then MsgBox Format(n) & "/" & Format(m)
Next
Next .
64 95 65
98
, ,
и
. Обсуждение этой
16 19 26
49
программы в Mcd отложим до будущего.
Упражнение 1. Какими цифрами следует заменить буквы в идеограмме СУК × СУК = БАРСУК, чтобы результат был верен?
Пример 7. Найти все трехзначные числа (числа Армстронга),
которые равны сумме кубов своих цифр. Здесь придется вложить друг
в друга три цикла:
В результате будут выданы дроби:
Dim i As Integer, j As Integer, k As Integer
For i = 1 To 9
For j = 1 To 9
For k = 1 To 9
If i^3 + j^3 + k^3 = (10 * i + j) * 10 + k Then _
MsgBox Format((10 * i + j) * 10 + k)
Next k
Next j
Next i
(бывает полезно для контроля после "Next" через пробел указывать
имя счетчика цикла, как выше; необходимости, однако, в этом нет).
В вычислительной практике циклы весьма успешно применяются
при анализе текстов, при нахождении значений бесконечных сумм,
произведений, предельных результатов итерационных и рекурсивных
алгоритмов, и т.д.
Пример 8. Построим функцию для вычисления биномиальных
0, если m < n
1 при m = n или n = 0,
n
m
коэффициентов Cm =  n  =  m!
Конечно, можно бы
n!(m - n)! в ост. сл.
в циклах пересчета вычислять факториалы. Но легко заметить, что факториалы можно определить рекурсивно (через самих себя) по форму1 при m = 0,
ле m! = 
Это уже подразумевает наличие пересчета.
(m-1)!∙m иначе.
Аналогично можно поступить и с биномиальными коэффициентами,
37
0, если m < n
1 при m = n или n = 0,
n
m
определив их следующим образом: Cm =  n  =  m n
m-n Cm-1 в ост. сл.
Таким образом, функцию можно оформить кодом:
Function C(m As Integer, n As Integer) As Integer
Dim i As Integer, r As Integer
Select Case m
Case Is < n: r = 0
Case n: r = 1
Case Else: r = 1
For i = n + 1 To m: r = r * i / (i - n): Next
End Select: C = r
End Function .
VBA и Mcd позволяют решить задачу еще проще – в обоих системах допускается рекурсивное определение функции и подпрограммы
"через себя" – внутри тела функция или подпрограмма вызывает себя с
другими параметрами (глубина рекурсии определяется допустимой памятью стека). В VBA соответствующий код примет вид:
Function C(m As Integer, n As Integer) As Integer
Dim i As Integer, r As Integer
Select Case m
Case Is < n: r = 0
Case n: r = 1
Case Else: r = С(m – 1, n) * m / (m – n)
'***рекурсия
End Select: C = r
End Function .
В Mcd определение функции выглядит еще проще:
C(m, n) : = if m < n, 0, if m = n, 1, C(m - 1, n)∙


m 
.
m - n
Пример 9. Рассмотрим алгоритм Эйлера для нахождения наибольшего общего делителя GCD двух натуральных чисел m и n: если
n делится на m, то DCD = m, иначе следует получить остаток r от деления m на n и искать наибольший общий делитель чисел n и r. Приведем соответствующие коды функций в VBA и Mcd:
VBA:
Mcd:
Function GCD(m As Integer, n As Integer) As Integer
If n Mod m = 0 Then GCD = m Else GCD = GCD(n Mod m, m)
End Function,
GCD(m,n) : = if(mod(n,m) = 0, m,GCD(mod(n,m), m)).
При достаточно глубокой рекурсии внутренние переменные определяются многократно, поэтому для определения этих переменных
целесообразно использовать инструкцию Static вместо Dim. Таким
38
образом определенные переменные сохраняются до конца работы
функции (подпрограммы) и, следовательно, отпадает необходимость
их переопределения. Рекурсии, несмотря на их внешнюю привлекательность и безусловное удобство, содержат скрытые опасности (поскольку определяющие их циклы не выписаны явно). Одна из них –
слишком глубокая (бесконечная) рекурсия, полностью "ломающая"
программу. Тем не менее, встречаются ситуации, в которых без рекурсий обойтись трудно и нет нужды пренебрегать ими без особых на
то причин.
Упражнение 2. Записать определение функции
2
x при x ≤ 0.1,
f(x) = 
с помощью рекурсии и без нее (цик2x
f(x-1) - f 2 иначе
x +
лом с условием).
Пример 10. Текст (строковое выражение) содержит целое число,
цифры которого перемешаны с другими символами. Найти квадрат
этого числа. Задача решается VBA-кодом:
Function AnalTxt(txt As String) As Variant
Dim s As String*1, i as integer, m As Integer, n As Long
m = 1: n = 0
For i = 1 To Len(txt): s = Mid(txt, i, 1)
Select Case s
Case "0" To "9": n = 10*n + VAL(s)
'***формирование числа
Case "-": If (m > 0) And (n = 0) Then m = -1
End Select
'***знак числа
Next
If n = 0 Then AnalTxt = "Чисел нет." Else AnalTxt = n*n
End Function,
или Mcd-кодом:
AnalTxt(txt) : =
m←1
n←0
for i ∈ 1 .. strlen(txt)
t ← substr(txt,i – 1, 1)
n ← 10∙n + str2num(t) if search("0123456789",t,0) ≥ 0
m ← -1 if t = "-" ∧ m = 1 ∧ n = 0 othetwise
if(n = 0, "no numbers", n2)
Так, например, при txt = "ква 7+ числа-5-то" функция возвратит результат 5625.
В этом примере впервые встретилось использование в VBA типа
Variant. Объекты этого типа могут содержать информацию произвольного базового типа. В данном случае этот тип позволяет функции
возвращать как текстовую, так и числовую информацию. В Mcd вид
39
возвращаемого результата определяется самой задачей и специально
не оговаривается.
Если бы потребовалось из текстовой информации извлечь последовательность целых чисел, разделенных произвольными символами, и просуммировать эти числа, то код программы был бы несколько иной. Постройте работающий код в качестве упражнения.
Как уже отмечалось, с помощью циклов удобно вычислять всевозможные суммы и произведения, особенно когда вычисления следует проводить с заданной точностью. При этом полезно сначала
провести предварительный анализ, выяснить алгоритм изменения слагаемых (сомножителей), затем использовать этот алгоритм при программировании решения конкретного задания.
Пример 11. Вычислить приближенное значение cos(x) с помощью
∞
x2n
степенного ряда cos(x) = n = 0 (-1)n
с погрешностью не более 
(2n)!
∞
= 0.00001. Здесь первые несколько слагаемых ряда  n = 0 qn можно
x2 x4 x6
x2n
записать в виде: 1 - + - + … Очевидно, qn = (-1)n
и qn-1 раз2 4! 6!
(2n)!
- x2
личаются лишь множителем (2n - 1) 2n , поэтому каждое новое слагаемое получается из предыдущего умножением на дробь указанного
вида. Задачу, таким образом, можно решить кодом в VBA:
Function Cos_x(x As Double) As Double
Din n As Integer , sum As Double, p As Double, q As Double
Const eps As Double = 0.0000001
sum = 1 : p = - x * x: q = 1
'***задано первое слагаемое и начальное значение суммы
Do
n = n + 2 : q = p * q / ( n * ( n - 1)) : sum = sum + q
Loop Until Abs(q) < eps
Cos_x = sum
End Function.
И кодом Mcd:
Cos_x(x) : =
sum ← 1
ε ← 0.0000001
q←1
n←0
while |q| > ε
n←n+2
-x2∙q
q←
n∙(n - 1)
sum ← sum + q
sum
40
Пример 12. Тот же косинус может быть представлен произведе∞
нием cos(x) =
4x
1 . При отсутствии сомножителей произП

2
n=1 
π (2n - 1)2
2
ведение по умолчанию считается равным единице. Далее, как и выше,
следует вычислять в цикле каждый сомножитель и домножать на него
предыдущий результат до тех пор, пока этот сомножитель не будет отличаться от единицы меньше допустимой погрешности. Приведем без
пояснений коды соответствующих функций в VBA и Mcd.
Function CosProd(x As Double) As Double
CosProd(x) : =
n←0
Dim prod As Double, r As Double
prod ← 1
Dim n As Integer, q As Double
r←
Const pi As Double = 3.141592653589
prod = 1: r = 4*x^2 / pi^2
Do: n = n + 1: q = 1 - r / (2*n - 1)^2
prod = prod * q
Loop Until Abs(q – 1) < 0.000001
CosProd = prod
End Function
q←0
while |q – 1| > 10-6
n←n+1
q ← 1 - r∙(2∙n - 1)-2
prod ← prod∙q
prod
4∙x2
π2
Пример 13. Рассмотрим более сложный случай. Требуется вычислять значения функции, представленной бесконечным рядом
∞
∑n=0
[ n]
(-1)
2n+1
n! x
, где [ ∙ ] обозначает целую часть чи2
3n 3 - 3 + ... + 3
сла, в знаменателе – ровно n вложенных (слагаемых) корней. Здесь
2n+1
pn
x
n!
каждое слагаемое qn есть дробь вида
, где pn =
, а rn =
n2
3 - rn
3
f(x) =
3+
3 + ... 3 (n вложенных корней, r0 = 0). Можно заметить, что
x2 n
pn = pn-1 m , где m1 = 3 и mn = 9∙mn-1. На каждом этапе, конечно же, нуn
жно вычислять dn = n и ее целую часть для определения знака слагаемого. Теперь все готово. Код функции в VBA примет следующий вид.
Function f(x As Double) As Double
Dim n As Integer, p As Double, q As Double, r As Double
Dim m As Long, sum As Double, d As Double, k As Integer
Const eps As Double = 0.000001
m = 3: p = x: sum = x / Sqr(3)
Do: n = n + 1: d = Sqr(n)
If (Int(d) Mod 2) > 0 Then k = -1 Else k = 1
p = p*d*x*x / m: r = Sqr(3 + r): q = k*p / Sqr(3 - r)
m = 9*m: sum = sum + q
Loop Until Abs(q) < eps
End Function .
41
Код в Mcd несущественно отличается от приведенного выше:
f(x) : =
ε ← 0.000001
n←0
m←3
p←x
sum ←
p
3
r←0
q←1
while |q| > ε
n←n+1
d← n
k ← if(mod(trunc(d),2) > 0, -1, 1)
p∙d∙x2
p←
m
r← 3+r
k∙p
q←
3-r
m ← 9∙m
sum ← sum + q
sum
(здесь из-за невозможности использовать цикл с постусловием пришлось ввести фиктивное значение первого слагаемого q = 1 для запуска цикла). Заметим, что запись кода сильно растянута.
Циклы с условием успешно используются для организации итерационных вычислительных процессов.
Пример 14. Пусть требуется найти с заданной точностью все
корни кубического многочлена p(x) = a0x3 + a1x2 + a2x + a3 (a0 ≠ 0). Один
действительный корень, во всяком случае, всегда существует. Поделим сначала все коэффициенты на а0, приведя многочлен к виду p(x) =
x3 + a1x2 + a2x + a3. Тогда, если а3 > 0, то существует отрицательный корень, в противном случае корень больше или равен нулю. Так что можно с возрастающим шагом двигаться вдоль числовой оси в нужном
направлении, пока многочлен не сменит знак, после чего шаг поиска
уменьшить и сменить направление движения. Процесс продолжается
до тех пор, пока шаг перемещения не будет достаточно мал. Найдя
приближенное значение корня x = x̂, можно поделить p(x) на x - x̂,
получив в результате квадратный трехчлен, корни которого мы уже
находить умеем (см. п. 1.5.2). Построим программу отыскания одного
действительного корня кубического многочлена, заданного своими
коэффициентами, результатом которой будет приближенное значение
корня и коэффициенты "оставшегося" квадратного трехчлена.
В VBA это будет не функция, а программа (поскольку возвращается не одно значение, а четыре), в Mcd – это функция. VBA – код:
42
Sub Poly3( ByRef a0 As Single, ByRef a1 As Single, _
ByRef a2 As Single, ByRef a3 As Single)
Dim x As Double, h As Double, s As Double, r As Double
Const eps As Double = 1E-10
a3 = a3 / a0: a2 = a2 / a0: a1 = a1 / a0: a0 = 1
x = 0: s = a3
If Abs(s) < eps Then Exit Sub
h = Sgn(-s)
While Abs(h) > eps
x = x + h: r = ((x + a1)*x + a2)*x + a3
If r*s ≥ 0 Then
h = 1.2*h
'***знак не меняется – увеличиваем шаг
Else
s = Sgn(r): h = -0.2*h
'***смена знака – область корня
End If
Wend
'***корень найден, делим многочлен на (х-корень)
'***пересчитываем коэффициенты:
a1 = a1 + x: a2 = a1*x + a2: a3 = x
End Sub .
Приведем Mcd-вариант программы (здесь для компактности в одной
строке записано несколько операторов присваивания, для исполнения
программу следует переписать по правилам, например, строка операторов
a3 ←
a3
a2
a1
, a2 ← , a1 ← , a0 ← 1
a0
a0
a0
должна быть записана как блок:
Poly3(a0, a1, a2, a3) : =
a3
a0
a2
a2 ←
a0
a1
a1 ←
a0
a0 ← 1
a3 ←
).
ε ← 10-10
a3
a2
a1
a3 ← , a2 ← , a1 ← , a0 ← 1
a0
a0
a0
x ← 0 , s ← a3 , (break) if |s| < ε, h ← sign(-s)
while |h| > ε
x ← x + h, r ← [(x ≠ a1)∙x + a2]∙x + a3
h ← 1.2∙h if r∙s ≥ 0
otherwise
s ← sign(r), h ← -0.2∙h
a1 ← a1 + x, a2 ← a1∙x + a2, a3 ← x
a0
a1
a2
a3
 
 
 
 1 
-1.5
Например, Poly3(2, -9, 10, -3) = 0.5 , т.е. для многочлена p(x) = 2x3  
 3 
9x2 + 10x – 3 найден корень х = 3 и "оставшийся" квадратный трехчлен
x2 -1.5x + 0.5 (с корнями х1 = 1, х2 = 0.5).
43
Пример 15. Система уравнений
y(x - 1) = 1,
 2
2
x = y + 1
имеет два действи-
тельных решения: в первом и третьем квадранте координатной плоскости. Полагая, например, х0 = 2, рассмотрим итерационный процесс
2
y
 n = xn - 1,

1 (n = 0, 1, 2, ...). Через 20 итераций (можно показать, что при
x
=
1
+
n+1
yn

выбранном начальном значении итерации сходятся к точному решению) три десятичных знака дробной части перестают меняться, процесс можно остановить: х ≈ 1.7166, у ≈ 1.2953. Если из уравнений исключить у, то получим (х3 + 1)(х - 2) + х = 0. Для этого уравнения итеx
рации xn+1 = 2 - x 3 +n 1 , x0 = 2, сходятся значительно быстрее – уже на
n
шестой итерации получается тот же результат. Приведем Mcd-код
программы, решающей последнее уравнение и возвращающей приближенное решение и число итераций (напишите соответствующий VBAкод самостоятельно).
1.716
ε ← 0.0001, n ← 0, x ← 2 = 
6 
y←x+1
while |x - y| ≥ ε
n ← n + 1, y ← x
x ← 2 - 3x
x +1
x 
n
Циклы удобно использовать для вычисления различных пределов.
Если аргумент f(x) стремится к некоторому конечному значению α, то
достаточно взять какое-нибудь допустимое значение х = а и полагать
a-α
xn = α + 2n , n = 0, 1, ... , точнее, можно выбрать шаг h = a - α и реализовать цикл
VBA:
Mcd:
x = a: h = a - alf: y = f(x)
Do: z = y: h = h/2: y = f(alf + h)
Loop Until Abs(y - z) < eps
x ← a, h ← a - α, y ← f(x), z ← y + 1
while |y - z| > ε
z ← y, h ← 0.5∙h, y ← f(α + h)
y
1+x
Пример 16. Вычислим lim 2 + x
x→ 1
1+x
f(x) = 2 + x
1- x
1-x
1- x
1-x
. Обозначим функцию
, положим х = 0, h = -1, ε = 0.00001 и, воспользовав-
шись приведенным алгоритмом, получим 0.816 (≈
2
).
3
44
Пределы в бесконечности, в принципе, считаются аналогично с
той лишь разницей, что выбранный шаг нужно не дробить (деля на
два, например), а увеличивать, умножая на какое-то число, например,
на два или больше.
2
х
х2 + 1
- 1 x
Пример 17. Вычислим lim x2 + 1
x→ ∞
. Обозначим функцию f(x) =
2
2
х - 1
x2 + 1


х +1
x
, положим х = 2, h = 10 и в цикле будем удваивать h:
Do: z = y: h = 2*h: y = f(h)
Loop Until Abs(y - z) < eps.
В результате получим единицу, как и следовало ожидать.
Упражнение 3. Вычислите все "замечательные" пределы.
Пример 18. Реализация этого примера существенно различается в
VBA и Mcd. Требуется найти наименьшее четырехзначное число n, для
которого n = m5, где m – количество единиц в двоичном представлении числа n. Здесь достаточно было бы для каждого n выяснять, есть
ли единица в соответствующем разряде, сравнивая его с соответствующей степенью двойки (с помощью связки And). Код решения задачи в
VBA выглядит достаточно прозрачно:
Dim n As Integer, m As Integer, k As Integer, i As Integer
For n = 1000 To 9999
m=0
'***счетчик единиц
For i = 1 To 15
If i = 1 Then k = 1 Else k = 2*k
'***сдвиг разряда влево
If n And k Then m = m + 1
'***совпадение разрядов
Next
If m^5 = n Then
MsgBox "n = " & Format(n) & ", m = " & Format(m)
Exit For
End If
Next .
В результате работы программы получено число 7776 с шестью единицами в двоичном представлении. Заметим, что в подсчете двоичных
единиц условие записано упрощенно: If n And k Then m = m + 1. Как
уже отмечено выше, логическое значение ячейки есть False, если она
пуста, в противном случае ее логическое значение есть True. Логические связки Or, And, Xor и отрицание Not действуют поразрядно, поэтому выражение n And k истинно (= True), если хоть в одном разряде у n и k одновременно стоят единицы, в противном случае значение
ложно.
45
Mcd, в общем, не приспособлен для простого анализа разрядов
чисел (в нем логические условия обрабатываются иначе). Здесь потребуется некоторая изворотливость с использованием операций над текстом. Во-первых, полезно будет создать функцию, возвращающую
двоичное представление десятичного целого числа (в виде текстового
выражения):
B(n) : = s ← ""
while n > 0
d ← mod(n,2), n ← trunc(0.5∙n)
s ← concat(if(d = 0,"0","1"), s)
s
Во-вторых, полезно создать функцию, возвращающую число единиц в
строке двоичного представления числа:
Num(n) : = s ← B(n), m ← 0
for i ∈ 0 .. strlen(s) – 1
m ← m + 1 if substr(s, i, 1) = "1"
m
Ну, а теперь сама программа будет выглядеть уже просто:
for n ∈ 1000 .. 9999
7.776×103
= 

6
s ← B(n), m ← Num(n)
if n = m5
n
return  
m
break
"nothing"
Напомним еще раз, что в Mcd-блоках несколько операторов, разделенных запятыми, в одной строке записаны лишь для компактности, в тексте рабочего листа каждый оператор должен записываться в отдельной строке.
1.7. МАССИВЫ
Массивы - группы однотипных данных с произвольным доступом в оперативной памяти (во внешней памяти соответствующие
группы данных называются файлами). По сути это таблицы с одним
или несколькими входами (одно или многомерные массивы) в соответствии с указанными индексами (т.е. с заданной нумерацией). В
VBA массивы определяются оператором Dim с указанием количества и диапазона изменения индексов (индексация по умолчанию начинается с нуля). При этом используются инструкции:
Dim ‹имя массива1›(n1) As ‹тип›, ‹имя массива2›(m2, n2) As ‹тип›
46
для одномерного и двумерного массивов: в первом массиве индексы
(т.е. номера элементов) изменяются от 0 до n1, второй массив
двухмерный, первый индекс меняется в пределах 0 - m2, второй 0 – n2.
Одномерный массив – это последовательность однотипных данных.
Двухмерный массив – плоская таблица, первый индекс – номер строки, второй – номер столбца элемента в таблице. Индексы указываются
в круглых скобках. По желанию индексацию можно начинать с
произвольного натурального числа, тогда инструкция определения
массива выглядит иначе:
Dim ‹имя массива›(m To n) As ‹тип›, ...
Здесь индекс может меняться в пределах от m до n.
Если размер массива заранее не известен и будет определен в программе в дальнейшем, то массив определяется вначале формально, без
указания размеров:
Dim ‹имя массива›() As ‹тип›,
затем перед его фактическим использованием можно указать его реальный размер инструкцией Redim ‹имя массива›(размер) (этот
оператор позволяет в процессе вычислений обнулять существующий
массив). В программе определение массива всегда должно располагаться до его фактического использования. Выборка элемента массива
осуществляется указанием его имени и индексов (в круглых скобках):
первый индекс – номер строки, второй – номер столбца, третий (если
есть) – номер "слоя", и т.д.. VBA позволяет использовать размерность
массивов до шестнадцати, хотя трудно представить себе реальную
размерность больше трех.
В Excel рабочий лист представляет собой плоскую таблицу с
более чем 2500000 ячеек с индексацией, по умолчанию начинающейся
с единицы. Эта стандартная таблица-массив имеет стандартное же имя
Cells(), ячейка в левом верхнем углу – Cells(1, 1), соседняя справа –
Cells(1, 2), и т.д. Второй ряд начинается с ячейки Cells(2, 1), далее
вправо Cells(2, 2), затем Cells(2, 3), ... . По умолчанию ячейки рабочего
листа имеют тип Variant, т.е. они могут содержать как числовую, так
и текстовую информацию. Поскольку ячейки – видимая часть
рабочего листа, в них можно вводить информацию непосредственно с
клавиатуры, а также выводить в них информацию в процессе работы
программы просто с помощью оператора присваивания. Например,
работая с конкретным рабочим листом (активный лист) оператор
присваивания Cells(1, 3) = "Вывод результата:"
поместит в
указанную ячейку приведенную фразу. А поскольку ячейки листа
имеют много полезных свойств, таких, например, как тип шрифта,
размер символов, цвет, и т.д., то такая таблица является удобным
47
инструментом ввода-вывода. Другие свойства рабочего листа и его
ячеек будут обсуждаться позднее по мере необходимости.
В Mcd массивы определяются указанием индексов (нижняя индексация) без скобок. Присваивание имени массива с максимальным
индексом некоторого значения (например, нуля) уже является определением этого массива. Например, запись A2,5 := 0 определит двумерный массив с тремя строками и шестью столбцами. Эта же запись в
определенном ранее массиве обнулит соответствующее значение.
Массивы фиксированного (не очень большого размера) можно
вводить, щелкнув мышкой по иконке "матрица" (см. рис. 6). Кроме
того, Mcd допускает использование ранжированных переменных (см.
п. 1.6) – одномерных массивов заданного типа, в которых содержимое
меняется по типу арифметической прогрессии с фиксированным
шагом. Например, запись i := 2, 2.5 .. 12 создаст переменную-массив
из 21 числа: 2, 2.5, 3, 3.5, 4, 4.5, ..., 12. Если переменную "ранжируем"
только первым и последним (целым) числом, то получим массив
значений арифметической прогрессии с единичным шагом. Это позволяет определять регулярные массивы произвольных размеров.
Например, определим квадратную матрицу (двумерный массив)
размером 1000×1000, диагональные элементы которой равны четырем,
соседние элементы – единицы, остальные нули:
m : = 1000
i : = 0 .. m - 1
n : = 1000
j : = 0 .. n - 1 Ai, j : = if(i = j, 4, if(|i - j| = 1, 1, 0)).
Для того, чтобы посмотреть созданную матрицу, достаточно набрать
ее имя и поставить после него знак равенства (рис. 7):
Рис. 7
48
Остальную часть массива можно увидеть, воспользовавшись прокруткой, которая появляется после щелчка мышкой по правому нижнему
углу выданной таблицы.
Mcd особенно приспособлен для работы с векторами и матрицами, снабжен для этого богатым набором встроенных операций и функций, таких, например, как транспонирование матриц, матричное и
векторное умножение, определение количества строк и столбцов матриц (функции rows и cols), определение последнего индекса вектора
(функция last), вычисление обратных (и псевдообратных – функция
geninv) матриц, выделение подматрицы (функция submatrix), вычисление определителя (обычнй знак модуля), упорядочение массива по
возрастанию содержимого (функция sort), склеивания соответствующих массивов горизонтально или вертикально (функции augment и
stack), решение линейных систем уравнений (функция lsolve), и много
других. Индексация массивов по умолчанию начинается с нуля, но
Mcd имеет специальную встроенную переменную ORIGIN, которая
позволяет изменить начало индексации, присвоив этой переменной
необходимое значение. В связи со всем этим значительная часть
программирования обработки массивов будет иллюстрироваться в
VBA с параллельными ссылками на сходные конструкции в Mcd.
Пример 1. Переписать содержимое одномерного массива размером 1 : m∙n в двумерный m×n массив. Код VBA:
Sub A_To_B(A() As Single, B() As Single, m As integer, n As Integer)
Dim k As Integer, i As Integer, j As Integer
k=0
For i = 1 To m
For j = 1 TO n
k = k + 1: B(i, j) = A(k)
Next
Next
End Sub .
Код Mcd (индексация начинается с нуля, для переписывания в Mcd
предыдущего кода "один к одному" следует положить ORIGIN : = 1):
A_To_B(A, m, n) : = k ← 0
for i∈ 0 .. m – 1
for j ∈ 0 .. n – 1
Bi, j ← Ak
k←k+1
B
Пример 2. Составить программу умножения двух матриц. Пусть
матрицы заданы массивами A(1 To m, 1 To k), B(1 To k, 1 To n), C(1
To m, 1 To n) и требуется вычислить C = A∙B.
49
Sub MProd(A() As Single, m As Integer, k As Integer, B() As Single, _
n As Integer, C() As Single)
Dim i As Integer, j As Integer, t As Integer, p As Single
For i = 1 To m
For j = 1 To n : p = 0
For t = 1 To k
p = p + A(i, t) * B(t, j) '***вычисление суммы сомножителей
Next: C(i, j) = p
Next
Next
End Sub .
В Mcd это просто C : = A∙B.
Заметим, что в Excel в меню f(x) "вставка функций" имеются
функции МОПРЕД и МУМНОЖ, вычисляющие определитель матрицы, записанной в ячейках рабочего листа, и произведение матриц.
Пример 3. Иногда бывает необходима специальная нумерация
элементов массива. Пусть, например, требуется перенумеровать элементы квадратного массива A(1 To n, 1 To n) параллельно побочной
диагонали, т. е. заполнить массив последовательно натуральными числами в порядке: A(1, 1) = 1, A(2, 1) = 2, A(1, 2) = 3, A(3, 1) = 4,
A(2, 2) = 5 и т. д. Заметим, что сумма индексов параллельно побочной диагонали остается постоянной. Этим и воспользуемся в приведенном ниже VBA-коде:
Sub SpecNum(A() As Integer, n As Integer)
Dim k As Integer, u As Integer, v As Integer, i As Integer, j As Integer, t As Integer
For k = 1 To 2 * n – 1
If k < n Then u = k Else u = n
'***u = min(k, n)
If k < n Then v = 1 Else v = k – n + 1
'***v = max(1, k – n + 1)
For i = u To v Step -1
t = t + 1: j = k + 1 – i: A(i, j) = t
Next
Next
End Sub .
Для n = 5 массив будет заполнен следующим образом:
Таблица 6
1
2
4
7
11
3
5
8
12
16
6
9
13
17
20
10
14
18
21
23
15
19
22
24
25
Соответствующий код в Mcd имеет вид (напомним: индексация
начинается с нуля, если не используется встроенная перемнная
ORIGIN):
50
SpecNum(n) : =
t←0
for k 0 .. 2∙n - 2
u ← min(k, n - 1)
v ← max(0, k - n + 1)
for i ∈ u .. v
t←t+1
Ai, k – i ← t
A
Пример 4. Вернемся к примеру 6 из п. 1.6 (правило сокращения
дробей). Теперь мы можем определить массив результата, который будет формироваться по мере вычислений и возвратится по окончании
расчетов. Код в Mcd выглядит следующим образом:
k←0
=
for m ∈ 10 .. 00
for n ∈ m + 1 .. 100
a ← trunc(0.1∙m), b ← mod(m, 10)
c ← trunc(0.1∙n), d ← mod(n, 10), q ← 0
if b ≠ 0
d
q ← if a = c
b
c
q ← if a = d
b
d
q ← if b = c
a
c
q ← if b = d
a
n
if q =
m
resk, 0 ← n, resk, 1 ← m
k←k+1
res
64
95
65
98
16
19
26
49
(здесь массив res формируется в процессе получения результата).
Пример 5. Для антисимметричной матрицы A с элементами
 2, i = j,

Ai,j =  1
найти сумму всех скалярных произведений столб i - j , i ≠ j
n-1
цов по формуле S =  i =1 
n
j=i+1
A‹ i ›  A‹ j ›, где n количество строк
(столбцов) матрицы А, верхний индекс указывает номер столбца матрицы. В VBA следующая программа решает задачу.
Function Scalar(n As Integer) As Single
Dim A() As Single, i As Integer, j As Integer, s As Single, k As Integer
Redim A(1 To n, 1 To n)
'***формирование матрицы
51
For i = 1 To n
For j = 1 To n
If i = j Then A(i, j) = 2 Else A(i , j) = 1 / (i - j)
Next
Next : s = 0
For i = 1 To n - 1
For j = i + 1 To n
For k = 1 To n
s = s + A(k, i) *A(k, j)
Next
Next
Next: Scalar = s
End Function .
В Mcd все можно записать значительно проще:
Scalar(n) : = for i ∈ 0 .. n - 1
for j ∈ 0 .. n – 1
Ai, j ← if i = j, 2,

n-2
∑
i=0
n-1
‹i›
(A
j=i+1
∑
‹j›
∙A
1 
i - j
)
Здесь использован символ суммирования, который
выбирается в меню анализа (см. рис. 8), вызываемом щелчком мышью по иконке
.
Как уже отмечалось (и это заметно по приводимым примерам), что в Mcd особенно удобно работать с векторами и матрицами. Пусть, например,
необходимо вычислять экспоненту матрицы с поA
∞
1
Рис. 8
n
мощью ряда exp(A) = e = ∑ n = 0 n! A . В VBA пришлось бы создавать
подпрограммы умножения матриц (см. пример 2), сложения матриц,
оценки максимального по модулю элемента (нормы матрицы), деления матрицы на число. Mcd справляется с этим совсем просто:
Exp(A) : =
ε ← 0.00001, n ← 0
q ← identity(cols(A)), S ← q
→
while max |q| > ε
n←n+1
q ← n-1∙q∙A
S←S+q
S
( )
Помимо уже использованных ранее встроенных функций здесь участвует функция identity(), возвращающая единичную матрицу указанно→
го (в качестве аргумента) размера, и операция векторизации (f(M), см.
52
рис. 6, - функция f применяется к каждому элементу массива М).
Функция max() возвращает наибольший элемент из списка аргумен 2 -1 0 
тов. В частности, для матрицы A=  -1 3 -2  функция вычислит зна 0 -2 1 
 15.096 -23.829 12.071 
чение Exp(A) =  -23.829 63.066 -35.588 .
 12.829 -35.588 21.443 
Упражнение. Создайте соответствующую программу в VBA.
Пример 6. Рассмотрим еще пример, где использование массивов
играет вспомогательную роль. Пусть для заданного набора n натуральных чисел a1, a2, … , an требуется вычислить сумму
a1
S= ∑
j1= 0
a2
an
1
∑ … ∑ 1+ j + j +… + j .
1
2
n
j2= 0
jn= 0
Каждая отдельная сумма, естественно, вычисляется с помощью цикла
For … Next, но количество таких циклов заранее неизвестно. Можно
создать вектор счетчиков и с его помощью выполнить суммирование.
Приведем пример программы (функция Ubound() возвращает верхнюю границу одномерного массива) в VBA.
Function Summarize(a() As Integer) As Single
Dim n As Integer, p() As Integer, sum As Single
Dim r As integer, i As Integer, j As Integer
n = Ubound(a): Redim p(n): sum = 1
'***подготовка информации
Do: r = 0
For i = n To 0 Step -1
If p(i) < a(i) Then
p(i) = p(i) + 1
'***заполнение массива
For j = 0 To n: If j > i Then p(j) = 0
r = r + p(j)
'***суммирование знаменателя
Next
sum = sum + 1 / (r + 1): Exit For
'***прерывание цикла
End If
Next
Loop Until r = 0: Summarize = sum
End Function .
В Mcd, как уже отмечалось выше, средства циклических вычислений
весьма упрощены. Предусловие (по своему смыслу) требует предварительной подготовки условия для запуска цикла, конструкция Do ...
Loop отсутствует полностью, прерывание цикла (вместо Exit For) выполняет оператор break. В результате программа в Mcd выглядит несколько иначе (напомним еще раз, что на рабочем листе Mcd разрешается записывать лишь один оператор в строке, здесь это правило
нарушается в целях компактности и экономии места):
53
:
Summarize(a) : = n ← last(a), pn ← 0, sum ← 1
r←1
while r > 0
r←0
for i ∈ n .. 0
if pi < ai
pi ← pi + 1
for j ∈ 0 .. n
pj ← 0 if j > i
r ← r + pj
1
sum ← sum +
r+1
break
sum
1.7.1. Программные стэки
В программе можно организовать неизменяемый стэк данных,
используемых локально в данном месте. В DOS-версии Бейсика для
этой цели использовалась инструкция DATA, за которой следовал
произвольный набор данных. Данные можно было прочитать с помощью оператора READ по порядку слева направо (счетчик стэка можно
восстановить с помощью инструкции RESTORE). В VBA эти служебные слова несут другую нагрузку, поэтому такая удобная конструкция
упразднена. Использование типа Variant позволяет организовать аналогичную службу с более широкими возможностями. В переменную
типа Variant можно поместить информацию любого основного типа с
помощью оператора присваивания и "функции" Array, параметрами
которой являются элементы информации, разделенные запятыми.
Ссылка на них осуществляется так же, как на элементы массива, индексированного с нуля (можно изменить начало индексации инструкцией Option Base 1). Функция Ubound() возвращает верхний индекс этого массива. При использовании его в программе можно не знать объем
содержимого, при этом допускается следующий вид цикла пересчета:
For Each ‹переменная› In ‹массив› ... Next,
в этом случае будут выбираться все элементы массива по порядку.
Пример. Пусть, например, квадратный массив n×n заполнен
случайными целыми числами. Элемент массива будет называться
"горкой", если его значение больше всех значений его ближайших соседей. Нужно посчитать количество горок. Будем индексировать все
массивы с нуля. Заметим, что индексы ближайших соседей различаются лишь на единицу. Для элемента Ai, j его ближайшими соседями
будут Ai, j+1, Ai+1, j+1, Ai+1, j, Ai+1, j-1, Ai, j-1, Ai-1,j-1, Ai-1, j, Ai-1, j+1. Поэтому
54
можно завести массив изменения индексов Ind = Array("Инкремент",
0, 1, 1, 1, 1, 0, 1, -1, 0, -1, -1, -1, -1, 0, -1, 1) и с его помощью сравнивать
содержимое соседних ячеек. Приведем код VBA.
Function Hills(n As Integer) As Integer
Dim A() As Integer, i As Integer, j As Integer, k As Integer, b As Boolean
Dim ii As Integer, jj As Integer, s As Integer, Ind As Variant
Ind = Array("increment",0,1,1,1,1,0,1,-1,0,-1,-1,-1,-1,0,-1,1)
Redim A(n - 1, n - 1): Randomize Timer '***подготовка генерации сл. чисел
For i = 0 To n - 1
For j = 0 To n - 1
A(i, j) = Int(100*Rnd – 50)
'***создан массив случайных чисел
Next
Next
For i = 0 To n - 1
For j = 0 To n - 1
b = True
For s = 1 To 8
ii = Ind(2*s - 1): jj = Ind(2*s)
'***выбор индексов
If i+ii >=0 And i+ii < n And j+jj >=0 And j+jj < n Then
If A(i, j) <= A(i+ii, j+jj) Then
'***проверка на горку
b = False: Exit For
'***это – не горка
End If
End If
Next: If b Then k = k + 1
'***а это – горка
Next
Next: Hills = k
End Function .
Как уже указывалось, в Mcd массивы также имеют (по умолчанию)
тип Variant, но отсутствует логический тип, так что код выглядит
несколько иначе:
Hills(n) : = Ind ← ("Increment" 0 1 1 1 1 0 1 -1 0 -1 -1 -1 -1 0 -1 1)T
for i ∈ 0 .. n – 1
for j ∈ 0 .. n – 1
Ai, j ← trunc(rnd(100) – 50)
k←0
for i ∈ 0 .. n – 1
for j ∈ 0 .. n – 1
b←1
for s ∈ 1 .. 8
ii ← Ind2∙s – 1, jj ← Ind2∙s
if Ai, j ≤ Ai + ii, j + jj if i+ii ≥ 0 ∧ i+ii < n ∧ j+jj ≥ 0 ∧ j+jj < n
b ← 0, break
k ← k + 1 if b > 0
k
Замечательно, что в отличие от стэков DATA содержимое массивов
Array можно произвольно менять в программе.
55
1.7.2. Тип пользователя
Пользователь имеет право определить свой тип, обладающий
свойствами некоторых стандартных типов или типов, определенных
пользователем ранее. Свойства типа (они называются "полями") указываются внутри "скобок" Type ‹имя типа› ... End Type, а сам тип должен быть определен в отдельном модуле для того, чтобы компилятор
создал соответствующую конструкцию. При обращении к переменной
пользовательского типа название конкретного свойства (или поля)
отделяется от имени типа переменной точкой. Рассмотрим
Пример. Пусть имеется 10 фамилий некоторых лиц, о которых
следует хранить такую информацию: фамилия, возраст, пол, номер телефона. В отдельном модуле определим тип Person следующим образом:
Type Person
Name As String*10
Aged As Byte
Sex As Boolean
Telef As Long
End Type .
'***фамилия (не более 10 символов)
'***возраст
'***пол (муж.): истина - ложь
'***длинное целое число
Теперь можно создать массив в 10 персон стандартным образом,
например, Dim Staff(9) As Person (этот тип уже определен). Организуем ввод необходимой информации в цикле:
For i = 0 To 9
Staff(i). Name = InputBox("Введите фамилию", "","")
Staff(i). Aged = Val(InputBox("Введите возраст", "", ""))
Staff(i). Sex = InputBox("Введите пол: True (муж.), False (жен.)", "", "")
Staff(i). Telef = Val(InputBox("Введите номер телефона", "", ""))
Next .
Аналогичным образом можно и выводить информацию. Для сокращения записи можно использовать конструкцию With ‹имя› ... End With,
внутри которой указываются лишь обрабатываемые поля, предваренные точкой. Таким образом, предыдущий код может быть записан несколько короче:
For i = 0 To 9
With Staff(i)
.Name = InputBox("Введите фамилию", "","")
.Aged = Val(InputBox("Введите возраст", "", ""))
.Sex = InputBox("Введите пол: True (муж.), False (жен.)", "", "")
.Telef = Val(InputBox("Введите номер телефона", "", ""))
End With
Next .
Предположим теперь, что из всех данных нужно выбрать лишь мужчин старше 50 лет:
56
For i = 0 To Ubound(Staff)
With Staff(i)
If .Sex And .Aged > 50 Then _
MsgBox .Name & ", Aged " & Format(.Aged)
End With
Next .
Теперь предположим, что одно из свойств нашего типа тоже
пользовательское. Пусть это тип Student с полями: факультет, курс,
наличие стипендии (да, нет). Определим типы:
Type Student
Department As String
Course As Byte
Scholarship As Boolean
End Type
Type Person
Name As String*10
Aged As Byte
Sex As Boolean
Business As Student
Telef As Long
End Type .
и переменную Dim Casanova As Person. Теперь поле Business само
имеет тип пользователя и свои собственные поля. Для того, чтобы отметить факт получения стипендии, следует выполнить присваивание
Casanova.Business.Scholarship = True,
а чтобы заполнить все поля, можно использовать вложенные конструкции With ... End With:
With Casanova
.Name = ...
.Aged = ...
.Sex = ...
With .Business
.Department = ...
.Course = ...
.Scholarship = ...
End With
End With .
Отметим, что цикл For Each ... In ... Next с пользовательской
переменной не работает, он используется лишь с типом Variant.
57
1.7.3. Сортировка массивов
В практике обработки массивов часто требуется (для облегчения
поиска, например), чтобы информация содержалась в массиве в определенном порядке (числовая, например, в порядке возрастания значений, текстовая – в алфавитном порядке, и т.д.). Сортировка – довольно
распространенная операция над массивами, поэтому в Excel, например, она включена в стандартное меню, а Mcd имеет функции sort() –
сортировка одномерного массива (вектора) в порядке возрастания,
csort() – сортировка матрицы по заданному столбцу, rsort() – сортировка матрицы по данной строке.
Существует довольно много алгоритмов сортировки, поясним
лишь два самых простых, применимых к массивам произвольной размерности. Один – с выбором главного элемента, второй – метод "пузырька".
А. Выбор главного элемента. Будем упорядочивать массив по
возрастанию элементов: просматривается весь (одномерный) ряд значений, выбирается наименьшее из них и ставится на первое место,
затем среди оставшихся выбирается наименьшее и ставится на второе
место, и т.д. Для одномерного числового массива А(n) в VBA алгоритм
имеет вид:
For i = 0 To n: p = A(i): k = i
For j = i + 1 To n: q = A(j)
If q < p Then
p = q: k = j
End If
Next
q = A(i): A(i) = A(k): A(k) = q
Next .
'***выбор минимального элемента
'***перестановка элементов
Если бы требовалось упорядочить массив по убыванию, то следовало
бы знак неравенства в третьей строке заменить на противоположный.
Если массив двумерный, например, А(m, n) и его следует отсортировать по столбцу с номером s, то пришлось бы ввести дополнительный
цикл:
For i = 0 To m: p = A(i, s): k = i
For j = i + 1 To m: q = A(j, s)
If q < p Then
'***выбор минимального элемента
p = q: k = j
End If
Next
For j = 0 To n
q = A(i, j): A(i, j) = A(k, j): A(k, j) = q '***перестановка элементов
Next
Next .
Б. Метод "пузырька". В предыдущей ситуации в одномерном
массиве просматриваются все соседние пары. Если в какой-нибудь па-
58
ре нарушается условие порядка, то элементы этой пары меняются местами. После такого просмотра самый большой элемент переместится в
конец массива (бегущий "пузырек"). Далее просматривается массив с
начала до предпоследнего элемента и выполняется та же процедура
проверки. Затем до предпредпоследнего, и т.д. Приведем соответствующий код для одномерного массива A(n).
For i = n To 1 Step -1
For j = 0 To i – 1
If A(j) > A(j + 1) Then
q = A(j): A(j) = A(j + 1): A(j + 1) = A(j)
End If
Next
Next .
Аналогично предыдущему, если необходимо упорядочить двумерный массив А(m, n) по столбцу с номером s, то следует поступить в
соответствии с кодом:
For i = m To 1 Step -1
For j = 0 To i – 1
If A(j, s) > A(j + 1, s) Then
For k = 0 To n
q = A(j, k): A(j, k) = A(j + 1, k): A(j + 1, k) = A(j, k)
Next
End If
Next
Next .
По трудоемкости эти алгоритмы одинаковы, так что выбор определяется лишь личным предпочтением. В Mcd, как уже отмечено, сортировка входит в список встроенных функций и там нет необходимости в
выборе алгоритма.
Сложнее дело обстоит в случае создания упорядоченного массива. Это бывает полезно, когда поступает произвольная информация, но
хранить ее нужно в упорядоченном виде для дальнейшего использования. Как и выше, будем полагать, что нас интересует порядок по возрастанию значений (или алфавитный порядок). Тут возникает вопрос
вставки нового значения в существующий массив без нарушения порядка.
Рассмотрим популярный алгоритм двоичного выбора: выбранный
диапазон индексов массива делится пополам и выясняется, в какую
половину следует вводить данные, выбранная половина снова делится
пополам, и т.д. до тех пор, пока окончательный участок не будет содержать единственный элемент, сравнение с которым очевидно. Например, в список (-2, 0, 1.5, 7, 7.2, 11) нужно ввести число 8.6.
Очевидно, (так как 8.6 > 1.5) нужно выбрать вторую половину списка
(7, 7.2, 11). В ней в середине стоит число 7.2 < 8.6, значит, число
59
помещается между 7.2 и 11. Осталось передвинуть последнее число в
следующую позицию (возможно, увеличив размер массива), а в освободившееся место поместить 8.6. Таким образом, процесс вставки в
массив состоит из двух операций: первая – поиск места вставки, вторая – освобождение места для новой информации.
Запишем первую операцию – поиск места, т.е. индекса элемента
массива, после которого нужно вставлять новый. Идея алгоритма допускает рекурсивный поиск (см. п. 1.4). Запишем его в виде функции.
Function Index(a() As ‹тип›, b As ‹тип›, p As Integer, q As Integer) As Integer
Dim res As Integer, k As Integer
If b < a(p) Then
res = p – 1
ElseIf b > a(q) Then
res = q
ElseIf q – p = 1 Then
res = p
Else
k = (p + q) \ 2
'***целочисленное деление
If b < a(k) Then res = Index(a(), b, p, k) Else res = Index(a(), b, k, q)
End If: Index = res
End Function .
Вторая операция – вставка – реализуется проще: если возвращаемый предыдущей функцией индекс отрицательный (при индексации с
нуля), то все элементы массива нужно сдвинуть и в первую позицию
вставить новую информацию, иначе это нужно сделать с указанного
индекса (предполагается, что размер массива это позволяет):
Sub Insert(ByRef a() As ‹тип›, b As ‹тип›, n As Integer)
Dim i As Integer, m As Integer
m = Index(a(), b, 0, n)
If m < 0 Then
For i = n To 0 Step -1
a(i + 1) = a(i)
Next: a(0) = b
ElseIf m = n Then
a(n + 1) = b
Else
For i = n To m + 1 Step -1
a(i + 1) = a(i)
Next: a(m + 1) = b
End If
End Sub .
Текстовые массивы (списки) сортируются точно также, поскольку знаки "<", ">" сравнивают коды символов (лексикографически). Если сортируются массивы пользовательского типа, то в сравнении указывается то поле, по которому выполняется сортировка. Например, если необходимо организовать массив данных типа Person (пример п. 1.7.2) в
алфавитном порядке (по фамилиям), то в функции
60
Index(a() As Person, b As Person, p As Integer, q As Integer)
следует записывать сравнения в виде
If b.Name < a(p).Name Then
...
В Mcd, в целом, функции выглядят проще. Кроме того, встроенная
функция stack(▪, ▪, ▪) (объединение массивов по вертикали) позволяет
автоматически увеличивать массив данных до необходимых размеров.
Index(a, b, p, q) : =
res ← p - 1 if b < ap
otherwise
res ← q if b > aq
otherwise
res ← p if q - p = 1
otherwise
p+q
k ← trunc 
 2 
res ← if(b < ak, Index(a, b, p, k), Index(a, b, k, p)
res
Insert(a, b) : = a ← stack(a, (0)), n ← last(a), m ← Index(a, b, 0, n - 1)
if m < 0
for i ∈ n - 1 .. 0
ai + 1 ← ai
a0 ← b
an ← b if m = n – 1
otherwise
for i ∈ n - 1 .. m + 1
ai + 1 ← ai
am + 1 ← b
a
На первый взгляд, кажется проще простого набрать данные, как
попало, а потом отсортировать нужным образом (по крайней мере,
сортировка готового массива выглядит проще). Но если (например, в
базах данных, где размеры массивов превышают сотни и тысячи) информация постоянно пополняется и регулярно используется, то вопрос
о выборе алгоритма решается не столь однозначно.
Упражнение 1. Попробуйте создать массив из десяти случайных
чисел, равномерно распределенных на заданном отрезке и упорядоченных по возрастанию.
Рассмотрим пример, в котором выбор порядка играет определяющую роль. Это решение систем линейных уравнений методом Гаусса.
Суть метода в том, что выбираются последовательно диагональные
61
элементы матрицы системы, делятся соответствующие уравнения на
эти элементы (вместе с правой частью) и, далее, эти уравнения (теперь
уже с единичным элементом на диагонали) вычитаются из других уравнений с тем, чтобы в соответствующих столбцах получились нули. В
результате матрица системы уравнений становится единичной, а правая часть содержит решение. Алгоритм в таком простейшем виде содержит два "подводных камня". Первый – на диагонали в результате
преобразований может оказаться нуль, и алгоритм "сломается". Второй – на диагонали может оказаться довольно маленький, но отличный
от нуля, элемент, деление на который может привести к большим
ошибкам результата (т.н. неустойчивость). В практической реализации
алгоритма Гаусса поступают так: при выборе очередного столбца в
нем находится максимальный по абсолютной величине элемент. Он и
его строка становятся "ведущими" и переставляются со строкой, в которой берется диагональный элемент. Это снимает оба "камня": если
ведущий элемент ноль, то система уравнений вырождена и решать нечего, и, поскольку ведущий элемент максимальный, то возможная
ошибка минимизируется. Вот и все – в чистом виде алгоритм А: "выбор главного элемента". Приведем алгоритм с учетом указанных поправок в Mcd. Здесь удобно переставлять столбцы матриц (индексированные в верхних угловых скобках, см. рис. 6), поэтому расширенную
матрицу системы (с присоединенной с помощью функции augment
правой частью) полезно представить в транспонированном виде.
Gauss(A, b) : = A ← (augment(A, b))T, n ← cols(A) - 1
for i ∈ 0 .. n
p ← 0, m ← -1
for j∈ i .. n
q ← |Ai, j|
if q > p
p ← q, m ← j
if m < 0
return "degenerate", break
p ← (Ai, m)-1, b ← A‹i›, A‹i› ← A‹m›∙p
‹ ›
A m ← b if m > i
for j ∈ 0 .. n
A‹j› ← A‹j› - Ai, j∙A‹i› if j ≠ i
‹ n + 1›
(AT)
(помните, что каждый оператор следует писать в отдельной строке).
Упражнение 2. Запишите соответствующий код в VBA.
Упражнение 3. С помощью приведенного алгоритма Гаусса запишите программу вычисления определителя квадратной матрицы.
Заметим, что в Mcd системы линейных уравнений с матрицей А и
правой частью b можно решать с помощью встроенной функции
62
lsolve (A, b). Матрица может при этом не быть квадратной (для переопределенных систем уравнений реализован метод наименьших квадратов или псевдообратной матрицы, которую можно получить также с
помощью функции geninv). Определитель матрицы A вычисляется с
помощью прямых скобок |A| (для числа это абсолютная величина, для
вектора – длина).
1.8. ФАЙЛЫ
Файл - это последовательность записей на внешнем носителе информации. Обычно каждая информационная система организует файлы своим специальным образом, присоединяя к имени файла отличительную "типовую" добавку - расширение. Например, файлы в DOS
часто имеют расширение .com, .sys, .exe и др., файлы в WORD имеют
расширение .doc, . rtf, .htm и др., в EXCEL - расширение .xls, в PAINT
-.bmp, в MULTIMEDIA -.avi, .wav, и т.д. В Бейсике, в основном, создаются текстовые и двоичные файлы - без расширения (или с расширением, определяемым пользователем), либо файлы программ с расширением .bas. Visual Basic позволяет компилировать программы в файлы с расширением .exe, но в приложениях они остаются в формате
приложения. Mcd позволяет сохранять данные с расширением .prn,
.txt, а также обрабатывать некоторые графические и медиафайлы.
1.8.1 Файлы в VBA
По типу доступа в VBA организуются файлы последовательные
(включая бинарные) и файлы прямого доступа.
В последовательных файлах записи могут иметь произвольную длину и разделены на носителе специальным признаком конца.
Каждое обращение к такому файлу либо добавляет запись к уже существующим, либо считывает записи по очереди, начиная с первой. При
работе с такими файлами используются операторы открытия, работы,
закрытия файла.
Открытие файла осуществляется строкой
Open "устройство: \ имя" For ‹ действие › As # N,
 input 
где действие =  output  , т.е. ввод (считывание из файла), вывод
 append
(запись в файл), добавление (к записям в файле), N -номер, присвоенный файлу в программе. Если файла для вывода не существовало, то
оператор Open создает указанный файл.
Работа с файлами:
Input # N,‹ имя переменной › - считывание записи из файла N,
63
Print # N,‹ имя переменной › - запись в файл с номером N.
Иногда употребляются также операторы Write #N (записи разделяются запятыми, текстовая информация оформляется в кавычки - это
удобно, когда текст содержит знаки препинания) и LineInput # N для
чтения информации, записанной оператором Write.
Функции Loc и Lof возвращают номер записи и длину файла в
байтах. Логическая функция Eof(N) возвращает значение True, если
обработана последняя запись файла с номером N, иначе - значение
False.
Закрытие файла:
Close # N - закрывает файл с номером N. Если номер файла не
указан, то этот оператор закрывает все файлы.
Обмен с файлами происходит через буфер, в котором после работы может остаться информация, поэтому полезно в конце работы закрывать все файлы, чтобы не оставлять информацию в буфере обмена.
Оператор End заканчивает программу, закрывая все открытые файлы.
Оператор Kill # N уничтожает (закрытый) файл с номером N (освобождает его место в памяти, убирает его имя из каталога).
Пример 1. В последовательном файле My_inf требуется остаe -z + 1
вить только числа z, удовлетворяющие условию: z  (0, ), sin(z) < 2.
Откроем временный файл с именем Tempo в папке C:\Temp одновременно для записи и чтения, затем его уничтожим:
Sub Cons_File_Test()
Dim z A Single
Const pi As Single = 3.1415926
Open "C: \ Temp \ My_Inf" For Input As #1
Open "C: \ Temp \ Tempo" For Output As #2
Open "C: \ Temp \ Tempo" For Input As #3
Do: Input #1, z
If (z > 0) And (z < pi) And ((Exp( - z) + 1) / Sin(z) < 2) Then Print #2, z
Loop Until Eof(1)
Close #1: Open "C: \ Temp \ My_inf" For Output As #1
Do
Input #3, z: Print #1, z
Loop Until Eof(3)
Close: Kill #2, #3
End Sub .
В бинарных (двоичных) файлах обмен осуществляется по байтам
и, следовательно, необходимо аккуратно отслеживать объем обмениваемой информации. С другой стороны, эти файлы позволяют более
свободно распоряжаться структурой данных.
64
В файлах прямого доступа хранится только текстовая информация (так что можно создавать файл с расширением .txt), при этом
каждая запись имеет фиксированную длину, определяемую полем записи в буфере.
Открытие файла:
Open " устройство : \ имя" For Random As # N Len = M,
где N - номер, присвоенный файлу в программе, М - длина записи в
байтах. Закрывается файл стандартно оператором Close.
В Dos-Бейсике пользователь должен был сам определять структуру и размер буфера с помощью директивы
Field # N,‹ поле 1› AS ‹ имя 1›, ‹ поле 2› AS ‹ имя 2›, и т.д.,
где N -номер файла, ‹ поле i › - размер памяти в байтах, отводимой буферной переменной ‹ имя i ›, i = 1,2,..., сумма полей равна М.
В VBA эта директива отменена, и пользователь создает переменную типа String необходимого размера, либо указывает соответствующий пользовательский тип.
Работа:
Get # N, m, A -считывание записи с номером m из файла с номером N в переменную А (либо в буфер).
Put # N, m, A - запись значения переменной А (или содержимого
буфера обмена) в файл (m –я запись) с номером N.
Так как здесь обменивается информация только в символьном виде, то
числовую информацию полезно предварительно переводить в символьную, а при считывании снова переводить в числовую форму. Если
информация обменивается в пользовательском формате, то эти преобразования выполняются автоматически с помощью встроенных функций, в противном случае это нужно делать самостоятельно.
Пример 2. Пусть нас интересует информация (фамилия, возраст,
пол, телефон) о некоторых конкретных людях. Определим (в дополнительном модуле) пользовательский тип (см. п. 1.7.2)
Type Person
Name As String * 10
Age As Byte
Sex As Boolean
Tel ef As Long
End Type
65
и организуем ввод данных в файл прямого доступа с именем Test.txt в
папке C:\Temp.
Sub Create_File()
Dim friends As Person, m As Integer, s As String
Open "C:\Temp\test.txt" For Random As #1 Len = Len(friends)
With friends
Do: s = InputBox("input a name", "", "")
If s = "" Then Exit Do
.Name = s
.Age = Val(InputBox("input age", "", 0))
.Sex = InputBox("input sex: true as male", "", True)
.Telef = Val(InputBox("telefon", "", 0)): i = i + 1
Put #1, i, friends
Loop
End With
Close
End Sub .
Введем такую информацию: Николаев, 23, True, 648297, Спинстер, 16,
False, 909581, Трафф, 35, False, 635014, Васин, 27, True, 810071, Лимонов, 81, True, 375573. В результате получим файл следующего содержания:
Николаев яяiд
Спинстер б
Трафф # †° Васин яяW\♀ Лимонов Qяя»
- вся информация, кроме текстовой, нечитабельна, выполнена конвертация числовых данных в текстовый формат. При чтении все, тем не
менее, становится на свои места. Если же последнюю строчку цикла в
предыдущей программе заменить на
s = s & ", " & Format(.Age) & ", "
If .Sex Then s = s & "муж." Else s = s & "жен."
s = s & ", " & Format(.Telef)
Put #1, i, s
(преобразование к текстовому формату), и длину записи указать не
меньше 26, то содержание файла будет вполне информативным:
__Николаев, 23, муж., 648297__Спинстер, 16, жен., 909581__Трафф,
35, жен., 635014_____Васин, 27, муж., 810071_____Лимонов, 81,
муж., 375573 .
В отдельных приложениях есть свои особенности работы с файлами, о них будет сказано в своем месте.
1.8.2. Файлы в Mcd
Для обмена числовой и текстовой информацией в Mcd имеются
лишь три функции: WRITEPRN("путь к файлу"), которая помещается
слева от знака присваивания (справа – объект для записи), и функция
66
READPRN("путь к файлу"), которая записывается справа от знака
присваивания. Информация записывается, как правило, в том же виде,
в каком она представлена на рабочем листе (кроме ранжированных
переменных). Каждая запись производится в отдельный файл (после
очистки от предыдущей информации). Если необходимо дополнить
данные в файле информацией такого же формата, то можно использовать функцию APPENDPRN("путь к файлу"), стоящую слева от
знака присваивания. Например, в рабочем листе Mcd записана инфор"test"
1 2 3 4
мация: b := (-6 8 3 0) c :=  13  d :=  4 3 2 1 , то присваивание
 2 
3 4 1 2
WRITEPRN("C:\Temp\Test.txt") := b
поместит в файл Test.txt запись: -6 8 3 0 . Присваивание
WRITEPRN("C:\Temp\Test.txt") : = с
поместит в файл Test.txt запись:
// Datafile written by Mathcad
// 12/14/11 20:07:05
.MATRIX 0 0 3 1
"test" 13
2
Наконец, присваивание WRITEPRN("C:\Temp\Test.txt") : = d
поместит в файл Test.txt запись:
1
2
3
4
4
3
2
1
3
4
1
2
Таким образом, запись числовой информации сохраняет в файле структуру данных рабочего листа. Если же массив содержит разнородную
информацию, то файл оформляется "шапкой", оговаривающей структуру даннах. Чтение из файлов данных выполняется просто операцией
присваивания (таким образом сразу создается рабочий объект). Например, присваивание А : = READPRN("C:\Temp\Test.txt") создает объект со структурой данных файла, т.е. число, текст, вектор, матрица.
67
1.9. РАБОТА С ГРАФИЧЕСКОЙ ИНФОРМАЦИЕЙ
Dos-версии Бейсика (да, собственно, и других языков программирования) с возможностью непосредственного управления экраном
дисплея позволяли устанавливать специальный графический режим
отображения информации. В Бейсике это оператор Screen N, где N –
номер режима, определяющий возможность цветного отображения и
плотности (число пикселей по ширине и высоте экрана). Некоторые
специальные дополнительные операторы позволяли изображать на экране определенный класс линий. Перечислим некоторые из них.
Cls – очищает экран.
Circle(x,y),R[,c[,,[,S]]] - изображает окружность (или дугу) с центром в точке (х, у) (счет точек начинается слева направо и сверху
вниз) радиуса R цветом с кодом с,  и  - угловые меры начала
и конца дуги (если изображается не вся окружность), S степень
сжатия (если изображается эллипс или его дуга).
Сolor [b[,f]] - выбор цвета фона и палитры.
Draw"‹текстовая информация›"- изображение произвольной ломаной в соответствии со строкой информации, где указываются
команды:
Un - движение вверх на n позиций,
Dn - движение вниз на n позиций,
L,R,E,F,G,H соответственно указывают на движение влево, вправо на северо-восток, юго-восток, юго-запад, северо-запад.
Mx,y - команда перехода к точке с координатами (х, у).
Префикс В команд движения указывает на перемещение без изображения линии (просто "перенос пера"), префикс N указывает на движение с возвратом в исходную точку.
An - разрешает поворот фигуры на n прямых углов,
TAn - разрешает поворот на n градусов (против хода часов),
Сn - устанавливает код n цвета линии,
Pn,m - закрашивает область цветом с кодом n вплоть до границы цвета с кодом m,
Sn - введение масштабного коэффициента n.
Line(a, b) - (c, d) [,c[,B[F]]] - изображение прямой, соединяющей точки (a, b) и (c, d), цветом с кодом с. Признак В означает изображение прямоугольника с вершинами (a, b), (c, d), признак F (вместе с В) закрашивает прямоугольник указанным цветом. Если
предыдущая точка предполагается фиксированной (оператором
Line или Pset), то первый операнд можно опустить, оператор
Line принимает сокращенную форму: Line - (c,d) [,c[,B[F]]].
Get (a,b) - (c,d), A - пересылает экранное содержимое прямоугольника
68
с вершинами (a,b), (c,d) в ранее определенный массив А.
Put (x,y), A [,характер] - пересылает графическую информацию из
массива А на экран, начиная с точки (х,у). Характер указывает
взаимодействие информации с экраном : Pset, Preset, Xor, Or,
And.
Paint(x,y),c1,c2 - окрашивает область экрана, содержащую точку
(х,у), цветом с кодом с1 до границы цвета с кодом с2.
Pset(x,y),c - изображается на экране точка (х,у) цветом кода с.
Preset(x,y) - убирает точку (х,у) с экрана.
Point(x,y) - возвращает атрибут цвета точки (х,у).
Visual Basic оставил лишь некоторые из традиционных операторов, такие как Circle, Cls, Line, Pset, добавив к ним возможность масштабирования (оператор Scale) и установку толщины линии (Draw
Width). На специальных элементах управления (Form, Picture, Image)
можно помещать прямоугольники, эллипсы, круги (элементы Shape),
рамки (Frame), совмещать изображения (PaintPicture), печатать текст
(Print) с выбором шрифта, размера и цвета текста.
В приложениях, как правило, имеется возможность внедрения любого графического объекта (в том числе и объекта другого приложения). Кроме того, разрешается использование художественного текста
(панель меню WordArt) и изображение разнообразных автофигур (панель меню Рисование). В Excel, например, имеется возможность автоматического построения
всевозможных графиков
и диаграмм. В меню "мастер диаграмм" (иконка )
представлен богатый выбор графических изображений функциональных
зависимостей (см. рис. 9).
Допускается также использование графических
возможностей других пакетов (StatGraf, MatLab,
Mcd, и др.). Word и другие офисные приложения
разрешают использовать
графические возможности
Рис. 9
Excel, а также имеют свою
панель рисования. Все это значительно расширяет графические возможности приложений и в значительной степени снижает необходимость
69
программирования изображений. Некоторые особенности графики в
Excel и Word, тем не менее, будут оговорены позже.
Mcd не имеет своей собственной панели рисования, но позволяет
загружать произвольные рисунки из файлов, внедрять элементы Paint,
Excel, Word, и др. К собственной панели "графика" можно добраться,
щелкнув мышкой по иконке
. В результате появится меню графических возможностей (рис. 10). В этом меню (по порядку слева направо): построение плоских графиков,
масштабирование (лупа) выбранного участка диаграммы, оцифрование отдельных точек графика, график в полярной системе координат, график поверхности (3D), линии уровня, столбчатая диаграмма,
построение пространственных кривых и векторного поля. Ко всему прочему, Mcd имеет несколько
Рис. 10
встроенных функций обработки изображений таких,
например, как загрузка массива цветовой палитры файла изображения,
построение полиэдра, чтение и запись цветовых оттенков изображения, и т.д. Это позволяет в рамках Mcd выполнять анализ, фильтрацию, преобразование некоторых распространенных типов графических файлов (см. также п. 6.1).
1.10. ОТЛАДКА И ТРАССИРОВКА
Основная проверка синтаксиса VBA происходит в процессе компиляции программы, окончательная – при запуске. Синтаксически
правильный программный продукт может содержать алгоритмические
и другие ошибки, не видимые невооруженным глазом. Редактор VBA
(меню Debug, см. рис. 11) позволяет установить в проблемных местах точки остановки (Toggle Breakpoint, F9) и выполнить участок программы по шагам (F8).
В этом режиме при наведении курсора на
переменную высвечивается ее текущее
значение, что позволяет отслеживать процесс вычисления. Кроме того, в меню
View (см. рис. 12) можно открыть дополнительное окно (Watch Window) для текущего просмотра значений различных
объектов (их можно туда поместить, выбрав пункт Add Watch в меню Debug).
Рис. 11
Нажатие клавиш Shift + F8 позволяет избежать пошаговой трассировки при ссыл-
70
ках на функции и подпрограммы. Вернуться к нормальному режиму
можно, нажав клавишу F5. Непосредственные вычисления можно провести в окне прямых расчетов (Immediate Window, см. рис. 12), используя DOS-овский оператор Print. Например, если нас интересует
ASCII-код символа "#" клавиатуры, в этом окне можно набрать код:
print "Код # = ";ASC("#")
и нажать "Enter", получим
Код # = 35.
В некоторых случаях избежать сложной ситуации позволяет техника "захвата
ошибки" с помощью оператора
On Error GoTo ‹метка›.
При возникновении конфликта компилятор передает управление указанной метке, где пользователь сможет на нее прореагировать. Если реагировать на ситуацию
не нужно, можно использовать оператор
Resume Next.
Пусть, например, в программе требуРис. 12
ется считывание информации из файла, который может отсутствовать. Если файла нет, программа может использовать значения по умолчанию и продолжать работать.
...
On Error GoTo Check '***переход к метке Check при аварийной ситуации
Open ‹путь к файлу› For Input As #n
...
Exit Sub
Check: MsgBox "Файл не найден," & Chr(13) & _
"используются данные по умолчанию.", vbExclamation, "Error!"
... ‹восстанавливаются умолчания›
Resume Next
End Sub .
(такой обработчик ошибок следует помещать в конце программы, перед ним можно поставить выход из программы, чтобы предотвратить
обработку несуществующей ошибки в конце работы).
В Mcd, начиная с версии 13, также имеются средства отладки и
трассировки программ. В период компиляции или вычислений проблемное выражение или имя функции отмечается красным цветом, обозначая ошибку. Например, при попытке вычислить значение функции
71
30
f(x) =
∑
n=0
trunc(ln(n))
2∙n-1
∙ n!∙x
(-1)
n2
n
3 ∙ П (1 + k∙x)
k=0
при х = 1 Mcd сообщает, что фунМеню
кция неопределена. Щелчок пратрассировки
вой кнопкой мыши по "покраснеошибки
вшему" изображению откроет меню выявления ошибки (рис. 13).
Выбор в нем "Trace Error" вызывает подменю выбора ошибки
Рис. 13
(рис. 14). Щелчок мышкой по
п. "First" высвечивает красным цветом n под знаком логарифма (логарифм нуля недопустим) с комментарием:
Рис. 14
"This function is undefined".
Установив начало суммирования с единицы, снова пытаемся вычислить значение f(1). Снова проблема с комментарием: "Encountered a
floating point error" – переполнение, компилятор создал "плохую"
программу. Запишем свою программу для вычисления бесконечной
суммы (по аналогии с примером 13 из п. 1.6):
f(x) : = ε ← 0.00001, x2 ← x2, n ← 1, mn← 3
x
q←
, sum ← q
3∙(1 + x)
while |q| > ε
n ← n + 1, mn← 9∙mn
q∙x2∙ n
q←
mn∙(1 + n∙x)
k ← if(mod(trunc(ln(n)), 2) = 0, 1, -1)
sum ← sum + k∙q
sum
Программа легко справляется с задачей. Несложно представить эту
функцию графически (меню "плоский график", рис. 15).
Рис. 15
72
В приведенной программе индексированная переменная – не элемент
массива, здесь индекс – это "подпись", которая вводится нажатием точки после имени переменной, т.е. mn в данном случае единый символ
одной переменной. К сожалению, визуального различия между индексом и "подписью" нет. Это иногда приводит к незаметным ошибкам.
Кроме указанных возможностей Mcd имеет окно трассировки
(Trace Window в меню View) и панель инструментов отладки (Debug
в меню Tools, см. рис. 16), а также
встроенные функции trace и pause.
Аргументы этих функций позволяют выводить промежуточные значения в окно трассировки. Аналогично VBA имеется также оператор
on error (на панели программирования, см. рис. 5). При вставке в программу он принимает вид:
▪ on error ▪,
где левый квадратик предполаРис. 16
гает сообщение
об ошибке, правый содержит выражение с возможной ошибкой.
1.11. ОБЪЕКТНО-ОРИЕНТИРОВАННАЯ ИДЕОЛОГИЯ
С возрастанием сложности программных пакетов появилась потребность внедрения т.н. структурной методологии, в которой всякий
проект есть совокупность иерархических абстрактных уровней, которые позволяют четко структурировать программу, улучшая ее корректность и понимание. Основные ее принципы следующие:
1. принцип абстракции, умение до определенного уровня игнорировать детали,
2. принцип формальности – строгого методического подхода, подчинения правилам, определенной дисциплины,
3. принцип "разделяй и властвуй" – разбиение сложной проблемы
на совокупность мелких, легко решаемых, с понятными взаимосвязями, каждая может быть реализована в виде отдельного модуля со
своей структурой и поведением,
4. принцип иерархического упорядочения – связан с предыдущим,
определяет уровни независимости и подчиненности модулей.
Со временем оказалось возможным некоторые модули наделить
дополнительными свойствами, превратив их в самостоятельный объект программирования.
73
Объект характеризуется совокупностью свойств, событий, происходящих при взаимодействии с ним, методов, которыми объект
воздействует на окружающую среду (объединение в одном объекте
таких качеств называют инкапсуляцией).
И структурная, и объектно-ориентированная методологии преследуют цель построения иерархического дерева взаимодействий объектов, при этом непременно отражается наследование родительских
свойств (вышележащих объектов) дочерними (нижележащими) объектами. Многообразие форм проявления однотипных действий разными
объектами называют полиморфизмом. Excel – прекрасный пример
объектно-ориентированной методологии.
Объекты в Excel – это то, чем можно программно управлять, и с
помощью чего можно управлять. Приложения в Ms Excel создаются
путем объединения объектов с помощью VBA.
Самый верхний объект в иерархии – Application (приложение),
который включает в себя Workbooks (Workbook – рабочая книга), а
также связь с объектами Windows. Рабочая книга включает в себя
Worksheets (Worksheet, рабочий лист, их может быть много). Рабочий
лист содержит основные "кирпичики" конструкции приложения: Cells
(ячейки), Range (диапазон ячеек), Chart (диаграммы), Shape (геометрические формы), CommandBars (элементы управления), и т.д.
Каждый подчиненный объект можно отнести к свойствам родительского объекта. При ссылке или установлении свойств можно выписывать всю иерархию, отделяя дочерние объекты, свойства и методы от родительского точкой. Например, можно занести значение 1 в
ячейку А1 первого рабочего листа в первой рабочей книге открытого
приложения командой
Application.Workbooks(1).Worksheets(1).Range("A1").Value = 1
(здесь выписана вся иерархия – все родственники до последнего колена, каждый от другого отделен точкой – это признак подчинения). Можно поступить иначе: если предполагается работа с конкретным рабочим листом, то определить переменную типа Object инструкцией
Dim ‹имя› As Object,
присвоить переменной всех "родственников", после чего можно работать только с этой переменной, не нося за собой всю "родословную".
Нужно при этом помнить, что присваивание объектов выполняется с
помощью служебного слова Set. В данном примере:
Dim W As Object
Set W = Application.Workbooks(1).Worksheets(1)
W.Range("A1").Value = 1 .
74
Аналогичным образом можно менять свойства объектов. Например,
можно рабочему листу присвоить имя:
Worksheets(1).Name = "Graphics"
(теперь к рабочему листу можно обращаться по имени, это свойство
наследуется и его подчиненными объектами, т.е. их тоже можно именовать).
Разумеется, если к объекту Excel обращаются внутри этого Excel,
то ссылка на Application необязательна. Если в проекте только одна
книга, то и в ссылке на Workbooks нет необходимости. Если программа имеет дело с одним активным рабочим листом, то и на него ссылаться необязательно. Если в одном рабочем листе требуются данные из
другого листа (или книги), то ссылки на них необходимы.
Метод объекта является некоторой подпрограммой, часто с параметрами, поэтому и вызывается метод, как и всякая подпрограмма – по
имени, за которым следуют фактические параметры (без скобок). Если
в методе используются не все параметры (или с нарушением порядка),
то ссылка на параметр должна состоять из трех элементов: имени параметра, знака присваивания ": =", значения параметра. Например, требуется закрыть рабочую книгу с именем "Книга-1", сохранив изменения в ней, и сохранить ее в памяти под именем "TestBook". Строка соответствующего кода может выглядеть так:
Workbooks("Книга-1.xls").Close SaveChanges :
FileName :
= True,
_
= "C:\Temp\TestBook.xls", RouteWorkbook : = False
(пробел и подчеркивание – признак продолжения строки).
В конце этого пункта, в табл. 7, приведен краткий список некоторых свойств и методов базовых объектов изложенной иерархии.
Со всяким объектом, внедренным на рабочий лист, может быть
связана запускаемая программа (макрос). Например, внедрив (с помощью панели "Рисование") на рабочий лист круг с надписью "Пуск",
щелкнем по нему правой кнопкой
мыши. В появившемся меню (рис.
17) выберем пункт "Назначить макрос". В открывшемся диалоговом
говом окне (см. рис. 18) выберем
пункт "Создать" (изменив, если необходимо, имя макроса). В результате в новом модуле появится заготовка кода макроса (в данном
случае):
Рис. 17
75
Sub Овал1_Щелкнуть()
End Sub .
В теле этой подпрограммы может быть помещен произвольный код
работы с приложением, вызов любых подпрограмм и функций.
Рис. 18
Таким образом легко решается вопрос о запуске различных программ
с рабочего листа, доступ к редактору VBA, и пр. Готовые макросы можно запускать и прямо из меню: (разработчик) ⇒ макросы ⇒ макрос
(выбор) ⇒ запуск, или в редакторе VBA, выделив его имя курсором и
выбрав в меню команду Run (клавиша F5). Удобнее всего, конечно же,
использовать специальные элементы управления. Но о них – в следующем разделе.
Поскольку произвольные события рабочего листа могут управляться программно, Excel (и другие пакеты, использующие VBA) имеет
возможность автоматического создания макросов. Для этого достаточно войти в меню "Макросы", выбрать подменю "Начать запись" и,
нажав кнопку "запись", выполнять необходимые действия. По окончании щелкнуть кнопку "остановить запись". Во вновь созданном модуле будет записана готовая программа, реализующая все действия. В
общем, программа вполне работоспособная. Но, как всякий автоматический продукт, она может быть упрощена и улучшена. Во всяком
случае, на ее основе можно (научиться) создавать вполне приличные
рабочие приложения.
76
Таблица 7
Range
Worksheet Workbook Application
Объект
Свойства
Caption – надпись в заголовке,
Path – путь к каталогу Excel,
WindowState – состояние окна
(нормальное, свернутое, развернутое)
Методы
Calculate – вычисление всех
формул,
Help – вывод справки,
Quit – закрывает Excel,
Run – запускает
подпрограммы.
Name – имя рабочей книги,
Path – путь к файлу книги,
Saved – сохранение изменений (да,
нет)
Activate – активизация,
Close – закрывает книгу,
Protect – защищает книгу,
Save – сохраняет книгу,
SaveCopyAs – сохраняет в
новом файле.
Activate – активизация,
Calculate – вычисление всех
формул,
Dilete – удаляет лист,
Protect – защищает лист (аргумент password).
Index – номер листа,
Name – имя листа,
UsedRange – ссылка на дипазон
ячеек,
Visible – отображение – скрытие.
NumOfCells – количество ячеек,
Dependents – диапазон зависимых
ячеек,
Name – имя диапазона,
Value – значение в ячейках,
Formula – строка формул,
Text – форматированный текст значений.
Calculate – вычисление всех
формул,
ClearContents – очищает
содержимое,
Copy – копирует значения в
другой диапазон.
1.12. КЛАССЫ
Класс – это некоторая таксономическая единица, характеризующая объекты с общими свойствами и поведением. Например, класс
Кошачьих не определяет ни одну конкретную кошку, но характеризует всех их в общем, определяя их отличительные черты и поведение.
Определив класс, мы можем далее создавать и использовать объекты с
однотипными свойствами. Таким образом, класс удовлетворяет всем
основополагающим принципам объектно-ориентированной идеологии.
Как и любой объект, класс описывает свойства объектов, события, методы.
События – это способы управления классом, его реакцией на
внешние воздействия. Отметим два специальных события, присущие
всем классам: Initialize – возникает в момент создания нового объекта
класса, Terminate – возникает в момент уничтожения объекта.
77
Методы класса – это функциональные "обязанности" объектов.
Практически они представляют собой различные процедуры (Sub) и
функции (Function) для "внутреннего" пользования, скрытые (определенные как Private) и (или) открытые (определенные как Public),
образующие интерфейс класса.
По сути дела, пользовательский тип можно упрощенно рассматривать как (урезанный) пример класса. Класс элементов управления
CommandBars имеет свойства: Visible, Controls, Position, и др., поддерживает методы: Add, Delete, ShowPopUp, Reset, OnAction, и др.
Если, например, нужно добавить кнопки в новую панель, запускающие какие-то процедуры, можно воспользоваться кодом:
With Application.CommandBars.Add("Новая панель",False, True)
.Visible = True: .Position = msoBarleft
With .Controls
With .Add(msoControlButton)
.Caption = "Кнопка1"
.OnAction = "‹имя процедуры›"
End With
End With
End With .
1.12.1. Собственные классы
Для создания собственного класса нужно добавить в проект модуль класса: редактор VBA ⇒ Insert ⇒ Class Module ⇒ Properties
Window (или клавиша F4). В раскрывшейся панели можно изменить
его имя (по умолчанию) Class1 на рабочее имя класса. В открывшемся
листе редактора можно ввести все свойства класса (так же, как в типе
пользователя) затем события и методы в виде подпрограмм и функций, в которых свойства обрабатываются без имени класса (и без точек).
Пример 1. Создадим класс автомобилей с именем Auto. В поле
кода класса введем следующие свойства:
Public Num As Byte
Public Model As String
Public Age As Byte
Public PetName As String
Public Price As Integer
Public Run As Single
Public Velocity As Byte
'***номер по порядку
'***модель автомобиля
'***возраст
'***кличка
'***цена в тыс. евро
'***пробег (км.)
'***скорость км./ч.
Запишем событие инициализации (создания по умолчанию) объекта
класса:
Public Sub Init()
Age = 30 * Rnd + 1: Velocity = 0
Model = "": PetName = "": Num = 0
78
Run = 100000 * Rnd: Price = 500 * Rnd
End Sub,
метод, возвращающий полную информацию об автомобиле:
Public Function Info() As String
Info = Format(Num) & ". " & Model & " - " & PetName & ": возраст " & _
Format(Age) & ", пробег " & Format(Run) & " км., цена " _
& Format(Price) & " тыс. евро"
End Function.
Добавим также возможность изменять скорость конкретного автомобиля (если скорость превысит некоторую величину, автомобиль сломается):
Public Sub SpeedUp()
Randomize Timer
Velocity = Velocity + 10
'***увеличение скорости
If Velocity > 240 * Rnd Then
Velocity = 0: Model = ""
End If
End Sub .
Поместим на рабочий лист три надписи: "Добавить", "Показать" и
"Поехали!". С каждй надписью свяжем одноименный запускаемый ей
макрос (в модуле1).
Public n As Byte, k As Byte, AutoList(10) As Auto, a As Auto
Sub Добавить()
Randomize Timer
n = n + 1: Set a = New Auto: a.Init
'***создание объекта
With a
.Model = InputBox("Название модели", "", "") '***ввод данных
.PetName = InputBox("Прозвище", "", "")
.Num = n
'***присвоение номера
End With
Set AutoList(n) = a
'***занесение в массив
Cells(n, 1) = a.Info
'***и на рабочий лист
End Sub
Sub Показать()
k = Val(InputBox("Выберите номер автомобиля", "", 1))
If k > n Then
MsgBox "Слишком большой номер", vbCritical, ""
Exit Sub
End If
Set a = AutoList(k): MsgBox "Вы выбрали" & Chr(13) & a.Info
End Sub
Sub Поехали()
Dim i As Byte
With a
'***вывод скорости
.SpeedUp: Cells(11, 1) = "Скорость": Cells(11, 2) = .Velocity
If .Velocity = 0 Then
MsgBox "Ваш " & .PetName & " кончился!", vbExclamation
Set AutoList(k) = Nothing
'***уничтожение объекта
79
For i = 1 To 10
'***обновление информации
If i < k Then
Cells(i, 1) = AutoList(i).Info
ElseIf i < n Then
Cells(i, 1) = AutoList(i + 1).Info
Else
Cells(i, 1) = ""
End If
Next
End If
End With
End Sub .
Теперь, несколько раз щелкнув по надписи "Добавить", введем информацию: Ferrary, Jack, Volvo, Gerta, Jaguar, Kiddy, BMW, Satyr. В ячейках С(1, 1) – С(4, 1) появится (например) текст:
1. Ferrary - Jack: возраст 4, пробег 60036,43 км., цена 338 тыс. евро
2. Volvo - Gerta: возраст 17, пробег 97644,75 км., цена 219 тыс. евро
3. Jaguar - Kiddy: возраст 26, пробег 57455,11 км., цена 241 тыс. евро
4. BMW - Satyr: возраст 30, пробег 35054,38 км., цена 132 тыс. евро
Щелкнув по надписи "Показать", выберем номер 3 из списка. Щелкая
по надписи "Поехали!", будем увеличивать скорость авто. После скорости 50 появится сообщение "Ваш Kiddy кончился!".
Отметим для дальнейшего, что здесь большая часть переменных
определена вне макросов. Эти переменные, таким образом, являются
глобальными для этого модуля и сохраняют свои значения, пока не закончится работа модуля (в данном случае, проекта). Для принудительного сброса их значений в меню редактора VBA следует выбрать пункт Reset (квадратик).
Класс, как подпрограмма или функция, допускает рекурсивное
определение свойств. Это позволяет организовать динамическое распределение памяти явно, т. е. строить объекты, которые занимают
память в зависимости от поступающей информации (напоминает конструкцию, аналогичную указателям в языке Pascal). Таким образом,
при определении класса позволено указывать неявную ссылку на
создаваемый объект (т. е. делается ссылка не на сам объект, которого
еще нет, а на место в памяти, где этот объект будет находиться). При
поступлении информации неявная ссылка делается явной и память,
занимаемая объектами, динамически изменяется.
Пример 2. Пусть некоторое число человек, пересчитавшись по
порядку, встали в круг (за последним идет снова первый) и, как в детской “считалке”, требуется удалить из круга каждого k-го по счету.
Создадим пользовательский класс Circ (т.е. введем модуль класса и
дадим ему имя Circ) со свойствами:
80
Option Explicit
Public Num As Long
Public Pre As Circ
Public Nxt As Circ
'***требование явного определения свойств
'***номер по порядку
' ***ссылка на предыдущего в круге
'***ссылка на следующего в круге.
На листе Excel поместим три надписи: “Initia” – инициализация
класса переменных, “Add” – добавление в круг нового человека,
“Delete” – удаление из круга очередного k-го по счету, и создадим в
модуле1 одноименные макросы. с кодами:
Option Explicit
Dim first As New Circ
Dim last As New Circ
Dim cur As Circ
Dim count As Long
Dim k As Integer
'*** первый в круге
'***последний в круге
'***текущий объект “считалки”
'***счетчик – количество участников
'***модуль пересчета
Private Initia()
'***инициализация
k = Val(InputBox("Какого по счету выбирать?", "", 2))
Set first.Nxt = last : first.Num = 1
Set first.Pre = last ; count = 2
'***формирование “круга”
Set last.Pre = first : last.Num = 2
'***из двух человек
Set last.Nxt = first
Cells(1, 1) = "Содержание круга": Cells(2, 1) = ""
Set cur = Nothing
'***пустой объект
End Sub
Private Sub Add()
'***добавление в круг
Dim ncell As New Circ
If count < 2 Then
MsgBox "Начните с инициализации!"
End If
count = count + 1
ncell.Num = last.Num : last.Num = count
Set ncell.Pre = last.Pre: Set ncell.Nxt = last
Set last.Pre.Nxt = ncell : Set last.Pre = ncell
Display
'***вывод информации в ячейку А2
End Sub
Private Sub Delete()
'***удаление из круга k-го по счету
Dim m As Long, i As Long
If k < 2 Then Exit Sub
If count = 1 then
MsgBox “Счет закончен” : Exit Sub
End If
For i = 1 To k
If cur Is Nothing And i = 1 Then
Set cur = first
Else
Set cur = cur.Nxt : m = cur.Num
'***переход по ссылке
End if
Next : MsgBox “Выбрали” & Format(m) & “-го”
Set cur.Pre.Nxt = cur.Nxt
Set cur.Nxt.Pre = cur.Pre
'***изменение ссылки
81
Count = count – 1 : Display
End Sub
'***вывод
Private Sub Display()
'***вывод информации в ячейку А2
Dim cell As Circ, txt As String, i As long
If cur Is Nothing Then Set cell = first Else Set cell = cur.Nxt
txt = Format(cell.Num)
For i = 1 To count – 1 : Set cell = cell.Nxt 'переход к следующему в очереди
txt = txt & ", " & Format(cell.Num)
Next
Cells(2, 1) = txt
End Sub .
Щелчок по надписи "Initia" создает простейший круг из двух человек.
По надписи "Add" - добавляет в круг еще одного человека со следующим номером. Номера участников "считалки" (подпрограммий
Display) выводятся в ячейку А2 (cells(2, 1)) рабочего листа. Размер
круга ограничивается форматом Long целых чисел. В диалоговом окне
процедуры Initia вводится модуль пересчета k. Щелчок по надписи
"Delete" удаляет из круга k-го участника, считая от последнего удаления (или от первого, если удалений еще не было). Схему ссылок в этом
примере можно представить наглядно в следующем виде (рис. 19):
Num(1)
Num(i)
Num(i+1)
∙ Pre ∙∙∙ ∙ Pre
Nxt ∙
Nxt ∙
∙ Pre
Nxt ∙
Num(n)
∙∙∙ ∙ Pre
Nxt ∙
Рис. 19
Этот пример досаточно простой для того, чтобы использовать
конструирование собственного класса. Частично его можно реализовать в Mcd. Например, если круг участников "считалки" (массив Q)
создан, то удалить из него k-го участника можно функцией
Del(Q, k) : =
n ← last(Q)
m ← mod(k – 1, n + 1)
for i ∈ 0 .. n – 1
k ← mod(m + i + 1, n + 1)
Ri ← Qk
R
Так, например, удалив из круга участников (1, 2, ..., 10) седьмого,
функция возвратит значения (8, 9, 10, 1, 2, 3, 4, 5, 6).
Замечательно, что ссылок может быть сколько угодно, поэтому
такие конструкции удобны для организации работы с очередями, деревьями, базами данных. Например, при построении дерева ссылок (что
может использоваться для организации базы данных, упорядочения
82
вводимой информации в скрытой форме и др.) каждый элемент (ячейка, или узел дерева) должен иметь один “вход” (ссылку) и несколько
выход 1

"выходов" (тоже ссылки): 
узел
. Кроме того, каждый
вход

выход 2
узел должен нести какую-то смысловую информацию и информацию,
характеризующую этот узел. Так, при обходе дерева полезно знать,
посещался ли этот узел (логическое поле), номер этого узла (поле
целого типа), отношение к предыдущему узлу и т. д. Пусть в простейшем варианте двоичное дерево (один вход и не более двух выходов)
предназначено для анализа числовой информации. Можно ввести модуль класса BTree (в свойствах класса установим имя класса BTree):
Option Explicit
Public Bul As Boolean
Public Ind As Integer
Public Num As Long
Public Value As Single
Public Pre As BTree
Public Le As Btree
Public Ri As BTree
'*** признак посещения узла
'*** отношение с предыдущим узлом
'*** номер узла по порядку (счетчик)
'*** значение (информационное поле)
'*** cсылка на предыдущий узел
'*** ссылка на первый (левый) выход
'*** ссылка на второй (правый) выход.
Далее определим метод класса, устанавливающий для элемента класса
значение и порядковый номер, очищая остальные поля:
Public Sub Init(a As Single, i As Long)
Num = i : Value = a : Bul = True : Ind = 0
Set Pre = Nothing : Set Le = Nothing
Set Ri = Nothing
End Sub .
Ссылки Pre, Le, Ri являются в определении класса формальными. Они
становятся реальными при формировании объекта с помощью оператора New BTree в общем разделе определений (раздел Dim ). Для
того, чтобы передвигаться по дереву от корня (первого узла) к какойнибудь вершине, выбирая левую или правую ветвь, можно рабочему
объекту (Current) присвоить значение первого узла (пусть его имя
First): Set Current = First, а затем переходить на левую (правую)
ветвь: Set Current = Current.Le (или Set Current = Current.Ri) до тех
пор, пока не придем в вершину, т. е. когда Current.Le Is Nothing или
Current.Ri Is Nothing. Присваивание осуществляется со всеми
фактическими связями. Таким образом, если необходимо в нужном
месте сделать изменения в построенном дереве, можно использовать
рабочую ячейку для необходимой ссылки. Например, если рабочая
ячейка оказалась левой ветвью (это можно узнать по ее индексу –
свойство Ind), то изменить свойство Bul соответствующего узла
дерева можно с помощью двойной ссылки: Current.Pre.Le.Bul =
False, так как ссылки здесь уже фактические.
83
1.12.2. Коллекции
Коллекции – это набор объектов, объединенных общим именем,
не обязательно одного класса, со следующими общими свойствами и
методами:
свойство Count – возвращает общее число объектов в коллекции,
свойство Item – возвращает объект из коллекции,
метод Add – добавляет объект в коллекцию,
метод Remove – удаляет объект из коллекции.
Для объявления пользовательской коллекции применяется тип данных Collection (с предваряющим служебным словом New, всякий новый объект создается с этим служебным словом). Присваивание значения объекту выполняется после служебного слова Set. Уничтожить
(или обнулить) объект можно присваиванием ему значения Nothing.
Для организации цикла (пересчета) с элементами коллекции служит
конструкция: For Each ... Next (как с массивами типа Variant).
Пример. Пусть нужно создать небольшой занумерованный список фамилий с телефонами. Определим модуль класса DataList со
свойствами:
Option Explicit
Public Num As Integer
Public Fam As string
Public Tel As long
'***порядковый номер в списке
'***имя представителя
'***номер телефона.
Определим событие (очистка информации)
Public Sub Clr()
Num = 0: Tel = 0: Fam = ""
End Sub
и метод (возвращает информацию об объекте)
Public function Inf() As String
Inf = Format(Num) & ". " & Fam & ", тел. " & Format(Tel)
End Function .
Поместим на рабочем листе две надписи "Добавить" и "Показать" и
назначим им макросы с такими же именами. Определим переменные
типа
Dim i As Integer
Dim NList As DataList
Dim Check As New Collection
'***счетчик в коллекции
'***объект созданного типа
'***коллекция объектов типа
и оформим содержание макросов:
Private Sub Добавить()
'***вводятся элементы коллекции
Set NList = New Datalist
'***создается объект
i = i+1
With NList
'***ввод данных
.Num = i : Fam = InputBox(“Введите имя”)
.Tel = Val(InputBox(“Введите номер телефона”))
84
End With
Check.Add NList
End Sub
'***добавление элемента коллекции
Private Sub Показать()
'*** “показывает” объект
i = Val(InputBox(“Введите номер элемента в списке”))
Set NList = Check.Item(i)
'***выбор элемента коллекции
MsgBox NList.Inf
'***метод Inf выдает содержимое объекта
End Sub .
Теперь при нажатии кнопки “Добавить” появляются окна ввода
фамилии и телефона и автоматически присваивается номер в коллекции. При нажатии кнопки “Показать” и вводе номера в коллекции на
экране появится информация об указанном объекте.
Коллекции замечательны тем, что они "собирают" объекты любой
природы. Это могут быть не только новые конструкции пользователя,
но также элементы управления, интерфейса, и др.
2. Элементы Excel
Кое-что об этом офисном пакете уже было сказано. Приведем
некоторый краткий ретроспективный обзор.
Немного истории.
1978 г. – VisiCalc (Dan Briclin, Bob Frankston) для Apple II,
1980 г. – SuperCalc для IBM PC, Lotus 1-2-3, Windows-3,
1985 г. – Multiplan для Makintosh,
1987 г. – Excel с использованием VBA и XLM,
1990-1994 гг. Каждый год – новая версия,
1995 г. – Excel-7 (макросы на VBA) совместимый с Windows-95,
1997 г. – Excel-97 (v/8) – прочно основан на VBA,
2000 г. и дальше Excel – интегрированная часть Office на основе VBA.
Excel, как инструмент, представляет собой
средства проведения презентаций,
средство ввода данных (с клавиатуры и из файла),
средство создания подходящей вычислительной среды,
генератор различных бланков,
текстовый процессор,
платформа простых игр.
Свойства и назначение Excel можно (кратко) свести к пунктам:
1. Файловая структура (листы собраны в рабочую книгу).
2. Использование VBA для управления и макросов.
85
3.
4.
5.
6.
7.
8.
Наличие настраиваемых элементов управления.
Использование диалоговых окон.
Настраиваемые меню и панели инструментов.
Наличие функций анализа данных.
Создание Data Access объектов, язык запросов.
Создание надстроек.
Иерархия объектов: все объекты Excel помимо собственных свойств
сохраняют наследственные по иерархии свойства. Иерархию кратко
можно представить следующим образом:
1. Приложение Excel – Application.
2. Рабочая книга – Workbooks("...").
3. Рабочий лист – Worksheets("...").
4. Диапазон ячеек – Range("... : ...") или Range(Cells(.,.), Cells(.,.)).
5. Ячейка – Cells(row, col).
6. Лист диаграммы – Chart.
7. Диаграмма.
8. Элементы форм – Shape.
9. VBProject.
10. Элементы управления – CommandBars.
11. Стили – Styles (Borders, Font, Interior).
12. Windows (панели – Panes).
Ссылки на конкретные объекты:
1. На функции рабочего листа: Application.WorksheetFunction.имя
функции.
2. В программе список функций VBA: x = Vba. (точка вызовет
раскрывающийся список встроенных функций).
3. Ссылка на Range:
а) свойство Range объекта Worksheet,
б) свойство Cells объекта Worksheet,
в) свойство Offset объекта Range,
например, Range("A1:D10").Cells(5) = 2000, Range("B2").Offset(a, b).
4. Текущие объекты: ActiveCell.Offset(.,.), ThisWorksheet, и т.д.
5. Консольный ввод данных: функция InputBox(запрос, заголовок,
по умолчанию, Xpos, Ypos,...) As String.
6. Вывод в диалоговое окно: MsgBox "текст", ... Можно выводить
много строк с помощью vbCrLf или vbNewLine (имитация возврата
каретки).
7. Функция MsgBox(запрос, кнопки, заголовок,...) позволяет реагировать на кнопки в условных операторах.
8. Одинаковые объекты автоматически формируют коллекцию.
9. Воспринимаются файлы с расширениями .xls, .wk4 (Lotus), .wq1,
.wq2, .wb1, .wb2 (Quattro Pro), .dbf (базы данных).
86
Excel допускает вставки:
1. Лист, строка (таблицы), столбец, ячейка, символ, диаграмма.
2. Функции рабочего листа (не VBA).
3. Имя диапазона или ячейки.
4. Рисунок (из файла, автофигуры, WordArt, и др.), схематическая
диаграмма.
5. Структура (часть листа может быть скрыта по желанию).
6. Объекты:
а) графические объекты (Bitmap, Photoshop, и др.),
б) Mcd-документ со всеми свойствами,
в) Microsoft Equation3 (вставка формул),
г) редактор VBA (со всеми формами и элементами управления),
д) документ MS Word (и все его свойства),
е) презентация MS Power Point и отдельные слайды,
ж) Windows Media Player,
з) календарь, и др.
Доступны надстройки, расширяющие возможности Excel:
1. Функции VBA для обработки данных (Analysis Tool Pack – VBA).
2. Мастер подстановок (формулы для поиска в списках).
3. Мастер суммирования (суммирование выбранных данных).
4. Пакет анализа (функции и интерфейс для обработки научных и
финансовых данных).
5. Пересчет в евро.
6. Поиск решения (инструмент для решения уравнений, систем, задач оптимизации).
7. Помощник по Интернету.
2.1. РАБОЧИЙ ЛИСТ
Рабочий лист представляет собой основную расчетную платформу рабочей книги. Настраиваемое меню позволяет получить вид листа,
удобный пользователю. Щелчок правой кнопкой мыши по ярлычку
листа вызывает меню (рис. 20), в
соответствии с которым можно
дать имя листу, удалить его, изменить цвет ярлычка, перейти в поле
кода этого листа редактора VBA.
В этом поле можно можно записать макрос
Sub WorkSheet_Activate()
...
End Sub,
Рис. 20
87
в котором заранее определяются какие-то установки рабочего листа.
Например, пользователю хотелось бы, чтобы прямоугольная область
A1:Q32 была синего цвета с красными линиями сетки. Для этого в макрос WorkSheet_Activate() достаточно вставить код:
With Range("A1:Q32")
.Interior.Color = vbBlue
.Cells.Borders.Color = vbRed
End With
(аналогичный макрос с шапкой Sub Workbook_Open позволяет выполнить необходимые действия и настройки при открытии Excel-проекта, событие BeforeClose подготавливает проект к закрытию, и т.д.).
Перетаскивание курсором границ столбцов (строк) сетки позволяет легко изменять их размер. Любая прямоугольная область листа
может быть объединена в одну ячейку (метод Merge объекта Range) с
именем верхней левой ячейки (или разъединена на исходную совокупность ячеек -Unmerge). Это бывает полезно, например, при необходимости использования шрифта большого формата или больших формул. В заданную ячейку (при выбранном формате) можно поместить
текстовую информацию, развернув ее произвольным образом (формат

шрифт

 текст 
ячеек
выравнивать
надпись), причем, если текст не помещается
в указанной ячейке, его изображение появляется и на "территории"
сосе-дних (справа) незанятых ячеек. Выбранную область можно залить
ка-ким-либо цветом, изменить в ней цвет, форму и стиль границ ячеек,
или вообще убрать сетку.
В разделе меню "Данные" (подраздел "группировка и струтура")
выбор пункта "Группировать" позволяет по желанию скрывать или открывать выделенную область строк или столбцов, демонстрируя суть
или подробности рабочего листа.
Меню "Вставка"
"Фигуры" (панель рисования) позволяет помещать на рабочий лист довольно широкий класс графических объектов
с возможностью различных стилей заливки и группировки изображений. Все это позволяет рабочий лист сделать привлекательным и наглядным. Приведем пример объявления, сделанного в рабочем листе
Excel (рис. 21, 22).
Рис. 21
88
Рис. 22
Здесь использована группировка (скрытие) столбцов A-J (кнопочка "+"
на рис. 21, нажатие ее открывает скрытые столбцы с рисунком и текстом объявления – рис. 22).
2.2. ЯЧЕЙКИ
В иерархии объектов ячейка Cells() рабочего листа является подобъектом объекта WorkSheet и свойством объекта Range того же рабочего листа. Стандартно ячейка представляет собой, как правило,
двухиндексный объект Cells(m, n), где m - номер строки листа, n – номер столбца, имеет много свойств и методов. Допускается также
нумерация по номерам строк и столбцов (стиль R1C1). Часто используемые свойства (наследство объекта Range): Value (значение), Name
(имя), Interior (внутренность) и др. Из методов выделим Activate,
Select - выбор конкретной ячейки. К выбранной ячейке можно уже
обращаться как к объекту ActiveCell или просто Selection, который
обладает свойствами иметь размер (высоту, ширину), имя, цвет,
шрифт, стиль заполнения и т. д. С некоторыми свойствами объектов
можно познакомиться, выбрав в меню редактора список объектов и их
свойств (Object Brouser, рис. 23).
Группа ячеек в Excel обычно описывается
как объект Range( ), - в скобках указывается диапазон. Например, Range("A3:C17") - прямоугольная группа ячеек от А3 (в левом верхнем углу)
до С17 (в правом нижнем углу), либо по индекРис. 23
89
сам: Range(Cells(3, 1), Cells(17, 3)). Объект Range может содержать
всего одну ячейку (в этом случае он отождествляется с Cells). Если
свойства ячейки не меняются (используются по умолчанию), ссылка
на "родителя" Range не обзательна.
Кроме свойств, присущих Cells, объект Range имеет свойства
Count (количество ячеек в объекте), Value (может принимать массив),
Borders (фиксирует границу области), Font (шрифт), ColumnWidth
(ширина столбца) и др. Из методов следует отметить Merge (объединение в одну ячейку по названию левой верхней), Unmerge (разъединение в первоначальное состояние), ClearContents (очистка),
Calculate (пересчет содержимого при изменении данных).
Пример 1. Пусть необходимо выделить ячейки с С3 по F20, объединить их, окаймляя границей, изменить в них цвет, шрифт и т. д.
Можно воспользоваться кодом:
Dim x As Variant, ARB As Variant
'***массив vb-констант
Dim RCells As Range
'***выбор объекта
ARB = Array(xlEdgeLeft, xlEdgeRight, xlEdgeTop, xlEdgeBottom) 'константы
Set RCells= Range("C3 : F20")
With RCells
.Select: .Merge: .Name = "Оплата"
With .Font:
'***Выбор свойств шрифта
.Name = "Arial": .Size = 14
.Shadow = True: .Underline = xlSingle
.Color = RGB(a, b, c) '***смесь цветов красного, зеленого, синего
End With
For Each x In ARB
With .Borders(x):
'***Выбор границы окаймления
.LineStyle = xlContinuous
.Weight = xlThick
.ColorIndex = 17
End With
Next
End With
(здесь RGB(a, b, c) - функция выбора цвета, a, b, c - целые числа от 0
до 255, соответственно доля красного, зеленого, синего цветов в смеси).
Пример 2. Пусть массив ячеек от А1 до Н20 заполнен числами
(например, случайными). Нужно выбрать те ячейки, значения в которых больше значений своих ближайших соседей (см. пример из п.
1.7.1), выделить эти ячейки цветом и шрифтом.
Sub Hills()
Dim m As byte, n As Byte, x As Integer, y As Integer, Check As Boolean
Dim A as variant, i As Byte, j As Byte, k As Byte, ii As Integer, jj As Integer
Randomize Timer
'*** массив изменений координат ячейки:
A = Array(-1,-1, -1, 0, -1, 1, 0, 1, 1, 1, 1, 0, 1, -1, 0, -1)
90
m = 20 : n = 8
For i = 1 To m: For j = 1 To n
Cells(i, j) = Int(100*Rnd - 50)
Next: Next
'***засеивание случайными числами
For i = 1 To m: For j = 1 To n
x = Cells(i, j).Value : Check = True
For k = 0 To 14 Step 2
ii = i + A(k) : jj = j + A(k + 1)
'***cравнение с 8 соседями
If ii > 0 And ii <= m And jj > 0 And jj <= n Then
y = Cells(ii, jj). Value
If y >= x Then
Check = False: Exit For
End If
End If
Next
If Check Then
Cells(i, j). Select
With Selection
.Font.Size = 14 : .Font.Bold = True 'Изменение шрифта
.Interior.ColorIndex = 3:
'***Красный цвет
End With
End If
Next : Next
End Sub .
Ячейка является одновременно окном ввода-вывода. В нее стандартно вводится форматированный текст, числа, даты, формулы. Поскольку Excel является зарубежным продуктом, возникает проблема
выбора разделителя целой и дробной части числа (в России для этой
цели используется запятая, в остальных странах – точка), которая легко решается в меню настройки. Поэтому, если возникают проблемы с
вводом дробных чисел, следут проверить настройки и формат ячеек. В
некоторых случаях при выводе чисел в ячейку последняя заполняется
символами "#". Это означает недостаток места для данного формата,
достаточно раздвинуть границы соответствующего столбца.
Ячейка является местом выполнения вычислений. В любую ячейку можно ввести произвольную (допустимую) формулу обработки
других ячеек, части данного (активного) или другого листа. Формула
вводится либо с помощью предваряющего символа "=", либо с помощью меню "f(x)" (вставка функций). Ссылки на другие ячейки, участвующие в вычислениях, реализуются либо выделением их курсором
мыши, либо непосредственным указанием этих ячеек в координатной
сетке рабочего листа. Ссылки могут быть абсолютными и относительными. Например, если в ячейке "А2" (ее адрес (2, 1) – вторая строка и
первый столбец) имеется ссылка на "F8" (ее адрес (8, 6)), то такая
ссылка считается относительной, поскольку при перемещении содержимого А2 (выделив и потащив мышью за границу области), например, в С9, ссылка изменится с F8 на H15 – перемещение ячейки перемещает и ее ссылки. Однако, если необходимо при перемещении со-
91
хранять столбец и (или) строку ссылки, то перед символом столбца
(номером строки) следует поставить знак "$". Так что если в предыдущем примере указать в А2 ссылку на "$F8", то при перемещении А2
в С9 ссылка изменится на F15, а если в А2 укажем ссылку на "$F$8",
то при любом перемещении ячейки А2 ссылка не изменится.
Среди стандартных операций над ячейками следует отметить
операцию "автозаполнения", позволяющую автоматически создавать
арифметическую прогрессию. Для этого в двух подряд идущих (вертикально) ячейках указываются два соседних члена арифметической
прогрессии, например, -1 и -0.8, выделяются курсором обе ячейки и рамка выделения за правый нижний уголок (курсор при этом принимает вид крестика – см. рис. 24) тянется вниз до необходимого
значения (в данном случае получится последовательность -1, -0.8, -0.6, -0.4, ...).
Если имеется ряд значений в идущих подряд
Рис. 24
ячейках и функциональная ссылка на первую из них,
то при "протягивании" этой функциональной ссылки можно получить
все последовательные значения вычисленной функции. Например, если ячейки А1:А21 заполнены числами 0, 0.15, 0.3, 0.45, ..., 3, а в ячейку
В1 вставлена формула "= SIN(A1)", то при протягивании В1 вниз до
В21 получим последовательность значений синуса: Sin(0), Sin(0.15),
Sin(0.3), ..., Sin(3) (влияние относительной ссылки).
Полезна также стандартная (встроенная) операция сортировки,
позволяющая по выбору сортировать группу ячеек (по возрастанию
или убыванию) и все связанные с ними ячейки.
2.3. ЭЛЕМЕНТЫ УПРАВЛЕНИЯ
Элементы управления практически используются для придания
листу функциональных возможностей. Элементы управления могут
быть различными по сложности, начиная от простых кнопок (Command
Button) до элементов управления мультимедиа. Excel позволяет
использовать как встроенные элементы управления, так и пользовательские. Это элементы ActiveX (ActiveX controls). Некоторое подмножество элементов управления является общим для всех приложений
Ms Office. В Excel панель элементов управления можно вызвать из
меню "Сервис"
VBA (версия не старше 2003 г.), либо "Разработчик" "Вставить элементы управления" (версия 2007 г. и старше, см.
рис. 25). При размещении элементов управления на рабочем листе
активизируется "Конструктор" (с пиктограммой "треугольниккарандаш"). В режиме крнструктора щелчок правой кнопкой мыши по
втавленому элементу вызывает меню, выбрав в котором пункт
92
исходный
текст
поле
флажок
переключатель
кнопка
полоса
прокрутки
список
поле со
списком
выключатель
счетчик
рисунок
другие
элементы
надпись
Рис. 25
"исходный текст", получим заготовку программы в VBA, запускаемой
этим элементом. Пользователь заполняет тело программы нужным ему
кодом. Программу можно запустить из рабочего листа, лишь отключив конструктор (для редактирования элемента управления конструктор должен быть включен).
Щелкнув мышкой на элементе управления панели и перенеся курсор на рабочий лист, увидим, что курсор преобразуется в крестик, которым можно определить на листе место для выбранного элемента
управления. Щелкнув правой кнопкой мыши на выбранном поле,
получим меню, где можно выбрать просмотр свойств элемента или
заготовку кода. Свойства элемента можно получить и непосредственно из панели инструментов (пиктограмма "свойства").
Еще раз заметим, что включенный конструктор позволяет изменять установленные на лист элементы управления, выключение конструктора приводит их в рабочее состояние.
Перечислим общие свойства элементов управления:
1. Name - имя (текст),
2. Autosize - установка наименьшего размера (True, False),
3. Enabled - доступность (True, False),
4. Font (шрифт),
5. Left, Top, Width, Height - положение на экране и размеры,
6. Locked - защита от редактирования (True, False),
7. Visible - визуализация (True, False),
8. PrintObject - печатание при печати листа (True, False).
93
Общие события (реакция на щелчок мыши, ввод кода):
1. Click - щелчок мышкой по (объекту),
2. DblClick - двойной щелчок мышкой,
3. KeyPress - нажатие клавиши на клавиатуре, если элемент активизирован (имеет "фокус"),
4. Got Focus - приобретение "фокуса",
5. Lost Focus - потеря "фокуса",
6. Mouse Down 
-"- Move  - реакция на действие мыши ,
-"Up 
7. Before DragOver 
- реакция на перетаскивание элемента .
-"- DropOrPaste 
Некоторые специфические свойства и методы.
Флажок (CheckBox) представляет возможность выбора.
Свойства: Caption - заголовок, текст рядом с флажком,
Value = True, если флажок установлен, False, если флажок
снят, Null - флажок неопределен (если свойство
TripleState = True),
LinkedCell - связанная сo свойством Value ячейка.
Событие: Click - отклик на изменение состояния флажка (запускает соответствующий код).
Кнопка (CommandButton) - обычно используется для запуска подпрограмм.
Свойства: Caption - текст на кнопке,
Picture - графическое изображение на кнопке (иконка),
TakeFocusOnClick - свойство брать "активность на себя"
(True, False). Желательно устанавливать False.
События: Click - ответ на нажатие кнопки (запуск кода).
Список (ListBox) позволяет выделить один или несколько элементов
списка, в зависимости от выделения запускает тот или иной код
(по типу Select Case). Можно добавить полосу прокрутки.
Свойства: List - массив строк списка,
ListCount - количество элементов в списке,
ListFillRange - диапазон листа с элементами списка,
ListIndex - индекс выбранного элемента списка,
Value - текст, выбранный в списке,
LinkedCell - ячейка рабочего листа, где появляется значение .Value,
Selected - массив булевских значений True, False в соответствии с выбранным элементом списка, и др.
События: Click – ответ на щелчок мышью, Change – реакция на
94
изменение списка, и др.
Выключатель (ToggleButton) по свойствам и событиям мало отличается от кнопки.
Поле (TextBox) - позволяет вводить текст в заданную область (и менять его программно).
Свойства: Text - устанавливает и возвращает текст,
Multiline - допускает многострочный текст(True, False),
MaxLenght - наибольшая длина текста (целое число),
LinkedCell - ячейка рабочего листа,содержащая отображаемый текст.
PassWordChar – символ, отображаемый при вводе пароля,
ScrollBars – наличие полосы прокрутки,
WordWrap – разрешение переноса на другую строку.
События: Change – реакция на изменение текста,
GotFocus – при фокусе на текстовом поле,
KeyPress – реакция на введенный символ, и др.
Переключатель (OptionButton) - по свойствам и событиям мало отличается от кнопки.
Поле со списком (ComboBox):
Свойства: как у списка (ListBox), и еще
ListRows - количество элементов в раскрывающемся списке.
Надпись (Label) - отображение надписей, нечто среднее между элементами поле и кнопка и имеет сходные с ними свойства и события. Существенная разница в том, что в поле надписи нельзя
вводить информацию с клавиатуры, вывод осуществляется в ее
свойстве "Caption".
Важным элементом управления для создания интерфейса и диалоговых окон является пользовательская форма (UserForm). Она
помещается на рабочий лист в меню редактора VBA: Insert
UserForm. Форма является контейнером для своих элементов управления, которые, в общем, повторяют элементы ActiveX, но имеют и
некоторые специфические, как, например, рамка (Frame), альтернативный список (TabStrip), и др. Кроме общих для всех форм свойств
следует отметить важное свойство ShowModal (по умолчанию True).
Это свойство запрещает какие-либо действия вне "сферы влияния"
формы, пока она открыта, т.е. находится на рабочем листе. Установив
значение ShowModal = False, можно от этого ограничения избавиться.
Форма появляется на рабочем листе лишь после выполнения команды
UserForm1.Show (если это только одна форма), вставленной, например, в код кнопки (CommandButton). Можно заставить форму появляться автоматически при активизации нужного рабочего листа. Для
этого в кодовой странице листа следует записать код:
95
Sub WorkSheet_Activate()
UserForm1.Show
End Sub .
В этой же подпрограмме можно установить все необходимые свойства
формы.
Пример 1. Создадим простейший арифмометр. Введем пользовательскую форму (UserForm1) со свойством ShowModal = False. Поместим на нее надписи: Label1 с текстом (Caption) "X = ", Label2 – "Y
=", Label3 – "Res:", Label4 – "Mem:", Label5 и Label6 с пустым
заголовком для вывода результата и содержимого "памяти". Рядом с
Label1 и Label2 разместим два текстовых окна TextBox1, TextBox2 для
ввода значений х и у (во всех случаях выберем шрифт – Font – так,
чтобы надписи были достаточно выразителтными). Справа от этих
элементов поместим список арифметических операций ListBox1,
выбрав подходящий шрифт, стиль окна (ListStyle = 1 –
fmListStyleOption), область заполнения (собственно список операций)
RowSource z1: z8 (за пределами видимости). В ячейки z1: z8 рабочего листа введем имена арифметических операций (пусть это будут: x +
y, x – y, x * y, x / y, sqr(x), x <-> y, Res <-> Mem, Mem -> x). Теперь,
дважды щелкнув мышкой по списку, получим в редактое VBA
заготовку кода: Private Sub ListBox1_Click() ... End Sub. Осталось
только заполнить его (щелчок мышкой по элементу списка возвращает
интекс выбранного элемента, индексация начинается с нуля):
Private Sub ListBox1_Click()
Dim x As Double, y As Double, z As Double
Const max As Double = 1E+35
x = Val(TextBox1.Text): y = Val(TextBox2.Text) 'считывание из текстовых окон
Select Case ListBox1.ListIndex
'***индекс выбранной операции
Case 0: z = x + y
Case 1: z = x - y
Case 2: z = x * y
Case 3
If Abs(x) > Abs(y) * max Then '***проверка возможности деления
Label5.Caption = "Деление на ноль": Exit Sub
End If
z=x/y
Case 4
If x = 0 Then
'***возможность извлечения корня
z=0
ElseIf x < 0 Then
Label5.Caption = "Отрицательное выражение"
Exit Sub
Else
z = Sqr(x)
End If
96
Case 5: z = x: x = y: y = z
TextBox1.Text = Str(x)
'***преобразование числа в текст
TextBox2.Text = Str(y)
Case 6: Label6.Caption = Label5.Caption
Case 7: TextBox1.Text = Label6.Caption
End Select
Label5.Caption = Str(z)
End Sub .
Таким образом, введя в текстовые поля значения х и у и выбрав мышкой в списке необходимую арифметическую операцию, в нижнем окне
получим необходимый результат. Вид формы калькулятора на рабочем листе представлен на рис. 26.
Рис. 26
Пример 2. Пример формирования и выбора меню (в кафе
автозаправочной станции). Поместим на рабочем листе кнопку
(CommandButton1) с надписью "Заказ" для вызова формы заявок и
формирования итоговой таблицы. Дадим ей имя Order. В ячейке Z1 (за
пределами видимости) будем хранить количество заказанных блюд, в
начале листа (левый верхний угол) будет сформирована таблица заказанных блюд с общей стоимостью. Введем, далее, рабочую форму
(UserForm1), на которой разместим надписи "Your choice" (выбор),
"Meals", "Drinks", кнопку (CommandButton1, это кнопка формы, не
листа) для завершения заказа с надписью "O'KEY!", и серию флажков
(CheckBox) с наименованиями соответствующих блюд (рис. 27).
Кнопка "Order" подготавливает
рабочий лист для оформления окончательной таблицы заказа и соответствующих цен. Кнопка пользовательской формы CommandButton завершает оформление заказа и закрывает
форму, оставляя на листе только таблицу-счет.
Рис. 27
97
Private Sub Order_Click()
Dim n As Byte, i As Byte, s As Single
'***подготовка таблицы
Range("a1:k5").ClearContents
'***очистка области рабочего листа
Range("z1").Value = n
'***счетчик заказанных блюд
Range("a1").Value = "ITEMS:"
'***заголовок: выбрано
Range("a2").Value = "ORDERED:"
'***объем заказа
Range("a3").Value = "SUMM:"
'***заказ на сумму
UserForm1.Show: s = 0
'***отображение формы заказа
n = Range("z1").Value
'***проверка количества заказанного
If n = 0 Then Exit Sub
'***выход, если заказ пустой
For i = 2 To n + 1: s = s + Cells(3, i).Value: Next
'***подсчет суммы к оплате
Cells(4, n).Value = "TOTAL:": Cells(4, n + 1).Value = s
Range(Cells(1, 1), Cells(4, n + 1)).Select
End Sub .
Приведем код обработки лишь одного флажка (CheckBox7 – заказ пива), остальные программируются аналогично.
Private Sub CheckBox7_Click()
Dim w As Integer, n As Byte
If CheckBox7.Value = True Then
w = Val(InputBox("Сколько бутылок Вас удовлетворит?", , 0))
If w = 0 Then
CheckBox7.Value = False: Exit Sub
End If:
With ActiveWorksheet
'***занесение заказа в таблицу-счет
n = .Range("z1").Value + 1
.Cells(1, n + 1).Value = " Beer"
.Cells(2, n + 1).Value = w
If w > 5 Then MsgBox "Туалет направо!", vbExclamation
.Cells(3, n + 1).Value = 60 * w
.Range("z1").Value = n
End With
End If
End Sub .
Кнопка на форме закрывает заказ:
Private Sub CommandButton1_Click()
CheckBox1.Value = False: CheckBox2.Value = False
CheckBox3.Value = False: CheckBox4.Value = False
CheckBox5.Value = False: CheckBox6.Value = False
CheckBox7.Value = False: CheckBox8.Value = False
Me.Hide
'***закрывает форму
End Sub .
'***сбрасывает флажки
Таблица-счет принимает вид (табл. 8):
Таблица 8
ITEMS:
ORDERED:
SUMM:
Pizza
4
600
Fish
3
240
Steak
Coffee
1
90
4
200
TOTAL:
Beer
8
480
1610
98
Заметим, что все элементы формы суть ее "дочерние" элементы, и
в этой ситуации закрытие формы может выглядеть, как команда
Me.Hide ("закрой меня") вместо UserForm1.Hide.
Использование других элементов управления в значительной степени следует технике приведенных примеров с учетом, разумеется,
индивидуальных особенностей элементов. Например, если на форме
размещена группа переключателей (OptionButton), то во всей группе
может быть выбран лишь один (в отличие от флажков – их можно
выбирать сколько угодно), который становится активным (все остальные сбрасываются). Если же часть переключателей разместить на форме внутри рамки (Frame – это своеобразный контейнер элементов управления), то пара выбор-сбрасывание будет "работать" либо внутри
рамки, либо вне ее. Таких рамок может быть сколько угодно. Другими
такими контейнерами являются элементы TabStrip и MultiPage.
2.4. ГРАФИЧЕСКИЕ СРЕДСТВА
Панель "Word Art" меню и возможность вставки произвольных
автофигур, естественно, расширяет изобразительные средства Excel.
Кроме того, как уже омечалось, Excel допускает вставку произвольных
графических объектов и имеет втроенную систему графического представления данных (см. п. 1.9 рис. 9).
Строить графики в Excel возможно, как минимум, четырьмя способами:
1. Использование Автофигур (меню: "Вид" → "Панели инструментов" → "Рисование" или "Вставка" → "Автофигуры"), меню которых содержит богатый набор инструментов, начиная от кривых
Безье (плоская кривая с заданными направлениями на концах) и
сплайнов (гладких полиномиальных кривых) до сложных шаблонов
инженерной графики. Меню позволяет легко редактировать (в режиме изменения узлов) уже построенные линии, выбирать их толщину, цвет, угол наклона и т. д.
2. Стандартное использование меню “Вставка диаграммы”. Курсором выбирается область листа для отображения графика, устанавливается формат и подписи к графикам. Графики могут быть реализованы как в общем тексте, так и на отдельной странице.
3. Вставка диаграммы из другого приложения (графический объект).
4. Построение графиков с помощью макросов. Здесь полезно заметить, что каждый графический объект листа это элемент объекта
SHAPES, являющегося подобъектом SHEET, поэтому всякая команда построения линии в Excel должна быть методом объекта
ActiveSheet.Shapes. Например, чтобы провести горизонтальную
99
стрелку, можно использовать код:
ActiveSheet.Shapes .AddLine(a, b, c, d) .Select
'*** (a, b) и (c, d) – координаты
With Selection .ShapeRange .Line
'*** начала и конца стрелки
.EndArrowheadStyle = msoArrowheadTriangle
.EndArrowheadLenght = msoArrowheadLenghtMedium
.EndArrowheadWidth = msoArrowheadWidthMedium
End With .
Для построения кривой по заданным координатам (x i, y i), i = 0…n,
можно использовать код (метод BuildFreeform – создание линии):
With ActiveSheet .Shapes .BuildFreeform(msoEditingAuto, x(0), y(0)) '***начало
For i = 1 To n
'***добавление узлов линии
.AddNodes msoSegmentCurve, msoEditingAuto, x(i), y(i)
Next
.ConvertToShape .Select '***оформление линии как графического объекта
End With .
Далее можно выбрать свойства кривой графика, например,
With Selection .ShapeRange .Line
.Weight = 3
'***толщина линии 3 пункта
.Style = msoLineSingle
'***однократная линия
.ForeColor.SchemeColor = 10
'***линия красного цвета
.Visible = msoTrue '***этот пункт обязателен, чтобы линия была видимой
End With .
В отличие от QBasic, где через точки с заданными координатами
проводится ломаная линия, здесь автоматически строится плавная
кривая.
Диаграмма, построенная стандартным способом через меню "Диаграмма" имеет много удобных для пользователя свойств (несколько
различных типов, выявление тренда, разброса точек и т. д.), помещается в отдельной панели диаграммы, которую можно закрепить в конкретном месте листа или поместить на отдельный лист и т. д. Рисованная кривая или график, построенный с помощью макроса может использовать богатые возможности панели "Рисование", допускает более
гибкий выбор формы, типа, цвета и художественного оформления.
Кроме того, такая диаграмма может быть помещена непосредственно в
текстовом поле листа и служить, например, фоном или элементом
оформления.
Рассмотрим каждый из указанных способов.
1. Построение с помощью автофигур. Рассмотроим функцию из п.
∞
[ln(n)]
2n - 1
(-1)
n! x
1.10: f(x) = ∑
. Запишем (вставив модуль) текст проn
2
n = 1 3n П (1 + kx)
k=1
граммы функции:
100
Function f(x As Single) As Single
Dim x2 As Double, n As Integer, mn As Long, q As Double
Dim k As Integer, sum As Double
Const eps As Double = 0.00001
x2 = x * x: n = 1: mn = 3: q = x / (3 * (1 + x)): sum = q
While Abs(q) >= eps
n = n + 1: mn = 9 * mn: q = q * x2 * Sqr(n) / (mn * (1 + n * x))
If Int(Log(n)) And 1 Then k = -1 Else k = 1
sum = sum + k * q
Wend: f = sum
End Function
(правильность вычислений можно проверить, вызвав в меню View редактора VBA окно Immediate Window). Заполним ячейки А1:А11 числами 0, 1, ..., 10, а в ячейку В1 введем функцию f: меню "Вставка
функций"
(полный список)
f с аргументом А1 (Enter). Затем за
правый нижний уголог прогягиваем значения ячеек до В11. Теперь по
этим данным можно построить рисунок графика: справа от таблицы с
помощью меню автофигур изображаем стрелки осей координат и в нужные места помещаем надписи с буквами Х и Y (для того, чтобы надписи выглядели как элементы текста, в меню "Формат надписи" →
"Цвета и линии" следует выбрать "нет заливки" и "нет линий"). Далее,
в меню "линии" (панель рисования) следует выбрать "кривую" и, пока
произвольным образом отмечая мышкой точки на линии, прорисовываем кривую. Щелчок правой кнопкой мыши по линии вызовет меню (рис.
28), в котором пункт "Начать изменение
узлов" активизирует отмеченные мышкой
точки на кривой. Эти точки можно "выправить", передвигая их нужным образом.
Наконец, в меню настройки объема применим стиль 4 ко всем линиям (можно изменить также цвет и толщину линий). В
результате получим рабочий лист в виде
рис. 29. Такой способ (не очень точный)
позволяет художественное оформление
Рис.28
графика.
Рис. 29
101
2. Меню "Вставка диаграммы" имеет богатый выбор возможностей.
В нашем частном случае следует выделить прямоугольную таблицу
значений аргументов и функции и в меню Диаграммы выбрать пункт
"Точечная диаграмма" (не "График", который используется для равномерной сетки аргумента), далее диалоговое меню проведет по всем
этапам построения графика (см. рис. 9).
3. Из других приложений вставка выполняется обычным образом
через буфер обмена: выделение → копирование (Ctr+C) → вставка
(Ctr+V). Например, если нам необходимо вставить в документ график
эллиптической спирали x(t) = 2 cos(t) + 0.2t, y(t) = 10 sin(t), то можно в
Mcd, например, ввести функции x(t) := 2∙cos(t) + 0.2∙t y(t) := 10∙sin(t)
и обратиться к меню "плоский график" (иконка ), выбрав диаграмму
без изображения осей, внизу диаграммы записав x(t), слева от поля диаграммы y(t). Результат (рис. 30) можно скопировать в буфер обмена и поместить на рабочий лист Excel.
4. Построим теперь график функции, изображенной выше с помощью автофигур, используя макросы. Пусть нам нужен гафик на весь
Рис. 30
рабочий лист. В меню выберем запись макроса с именем Graph. Изобразим (вставка автофигур) в нужном месте координатные оси и произвольную кривую (как в
первом случае) и остановим запись. В новом модуле текст макроса
имеет вид:
Sub Graph()
'
' Graph Макрос
' Макрос записан ‹дата›
'
'
ActiveSheet.Shapes.AddLine(47.4, 291, 594.6, 291.6).Select
Selection.ShapeRange.Line.EndArrowheadStyle = msoArrowheadTriangle
Selection.ShapeRange.Line.EndArrowheadLength = msoArrowheadLengthMedium
Selection.ShapeRange.Line.EndArrowheadWidth = msoArrowheadWidthMedium
Selection.ShapeRange.Flip msoFlipVertical
ActiveSheet.Shapes.AddLine(46.8, 9.6, 48#, 291.6).Select
Selection.ShapeRange.Line.EndArrowheadStyle = msoArrowheadTriangle
Selection.ShapeRange.Line.EndArrowheadLength = msoArrowheadLengthMedium
Selection.ShapeRange.Line.EndArrowheadWidth = msoArrowheadWidthMedium
Selection.ShapeRange.Flip msoFlipVertical
With ActiveSheet.Shapes.BuildFreeform(msoEditingAuto, 48#, 290.4)
.AddNodes msoSegmentCurve, msoEditingAuto, 61.8, 252#
.AddNodes msoSegmentCurve, msoEditingAuto, 92.4, 223.8
.AddNodes msoSegmentCurve, msoEditingAuto, 146.4, 205.8
.AddNodes msoSegmentCurve, msoEditingAuto, 258.6, 198#
.AddNodes msoSegmentCurve, msoEditingAuto, 408.6, 180#
102
.AddNodes msoSegmentCurve, msoEditingAuto, 574.2, 13.8
.ConvertToShape.Select
End With
End Sub .
В нем, очевидно, много лишнего. После "очистки" тело макроса будет
короче (сравните!):
ActiveSheet.Shapes.AddLine(47, 291, 595, 291).Select
With Selection.ShapeRange.Line
'***ось абсцисс
.EndArrowheadStyle = msoArrowheadTriangle
.EndArrowheadLength = msoArrowheadLengthMedium
.EndArrowheadWidth = msoArrowheadWidthMedium
End With
ActiveSheet.Shapes.AddLine(47, 291, 47, 9).Select
With Selection.ShapeRange.Line
'***ось ординат
.EndArrowheadStyle = msoArrowheadTriangle
.EndArrowheadLength = msoArrowheadLengthMedium
.EndArrowheadWidth = msoArrowheadWidthMedium
End With
With ActiveSheet.Shapes.BuildFreeform(msoEditingAuto, 48, 291)
' *** ... добавление узлов линии
.AddNodes msoSegmentCurve, msoEditingAuto, 574.2, 13.8
.ConvertToShape.Select
End With .
Таким образом, диапазон изменения аргумента 47 ... 595, функции
291 ... 9, следовательно, можно ввести масштаб (595-47)/10 = 54.8 для
х и (291-9)/0.38 ≈ 742.1 – для у (f(0) = 0, f(10) ≈ 0.38). Поэтому заполним тело макроса следующим кодом:
Sub Graph()
Dim x As Single, y As Single, h As Single, i As Integer
Const mx As Single = 54.8
Const my As Single = 742.1
ActiveSheet.Shapes.AddLine(47, 291, 595, 291).Select
With Selection.ShapeRange.Line
'***горизонтальная стрелка
.EndArrowheadStyle = msoArrowheadTriangle
.EndArrowheadLength = msoArrowheadLengthMedium
.EndArrowheadWidth = msoArrowheadWidthMedium
End With
ActiveSheet.Shapes.AddLine(47, 291, 47, 9).Select
With Selection.ShapeRange.Line
'***вертикальная стрелка
.EndArrowheadStyle = msoArrowheadTriangle
.EndArrowheadLength = msoArrowheadLengthMedium
.EndArrowheadWidth = msoArrowheadWidthMedium
End With: h = 0.1
'***рисование линии:
With ActiveSheet.Shapes.BuildFreeform(msoEditingAuto, 47, 291)
For i = 1 To 100: x = i * h: y = f(x)
x = 47 + mx * x: y = 291 - my * y
.AddNodes msoSegmentCurve, msoEditingAuto, x, y
Next
.ConvertToShape.Select
End With
103
'***форматирование линии
With Selection.ShapeRange.Line
.Weight = 3
.ForeColor.SchemeColor = 10
.Visible = msoTrue
End With
End Sub .
Запустить макрос можно из меню "Макросы", либо вставив надпись с
формулой и назначив ей макрос Graph. В результате получим график
рис. 31.
∞
f(x) =
∑
n=1
[ln(n)]
(-1)
n2
n! x
2n - 1
n
3 kП
(1 + kx)
=1
Рис. 31
2.5. ВЫЧИСЛЕНИЯ
Excel хорошо приспособлен для расчетов в таблицах (это табличный процессор). Он имеет богатый набор встроенных функций (см.
рис. 32), вызываемых из меню "Вставка функций" (иконка f(x)). В программе, как правило, используются стандартные встроенные функции
VBA, но есть возможность вызывать любую функцию рабочего листа с
помощью (свойство иерархии объектов) обращения к свойству
Application.WorksheetFunction. Например, если в программе необходимо вычислить среднее значение чисел 37, -11, 0, 2.15, 9, то можно
обратиться к функции Average (среднее значение) командой
Application.WorksheetFunction.Average(37, -11, 0, 2.15, 9).
Используя свойства ячеек рабочего листа, их массивов и набор встроенных функций, можно непосредственно в пределах каждого рабочего
листа выполнять довольно сложные расчеты. Кроме того, меню дополнительных надстроек позволяет использовать пакет анализа данных,
программы поиска решений в задачах подбора параметров, оптимизации, и т.д. В задачу пособия не входит подробный анализ всех
104
Рис. 32
свойств и возможностей пакета Excel, поэтому ограничимся лишь некоторыми демонстрационными примерами.
Пример 1. Найдем параметры линейной регрессии y = a + bx прямым вычислением и с использованием встроенных статистических
функций. Заполним ячейки А2:А21 значениями: ‹А2› = СЛЧИС() (случайное число из промежутка (0, 1) – аналог VBA-функции Rnd), далее,
А2 = А1 + СЛЧИС(), и т.д. В ячейку В2 вставим формулу "= Sin(A2/6)"
и протянем (за правый нижний угол) до В21, подучив таким образом
таблицу значений исследуемой функции. Параметры регрессии вычи−
x∙y - −
x ∙−
y
− . Поэтому в ячейку С2 вводим
сляются так: b =
, a =−
y - b∙x
2
−
2 −
x -x
формулу "= А2*А2" и протягиваем формулу вниз до С21, в D2 –
формулу "= А2*В2" и аналогично протягиваем вниз. Теперь нужно
вычислить средние значения: в ячейку А22 вводим формулу
"=СРЗНАЧ(A2:A21)" и протягиваем ее вправо до D22, получив таким
− . Теперь в ячейку Е23 вводим
образом средние значения −
x, −
y , x−2 и x∙y
формулу вычисления параметра b: "=(D22-A22*B22)/(C22-A22^2)", а в
С23 – формулу "=B22-E23*A22" – значения параметров получены. Для
сравнения прямой линии с исходными данными вычислим значения
регрессии a + bx: в ячейку Е2 введем формулу "=C$23+E$23*A2" и
протянем ее вниз до Е21 (здесь при протягивании ссылки на ячейки
С23 и Е23 – значения параметров а и b – должны быть абсолютными,
следовательно, "закреплены" символом "$"). В соседнем столбце F вычислим разность у - а - bx = e (отклонения). Выделив, наконец, область
А2:F21, обратимся к построению диаграммы (точечная диаграмма, см.
рис. 33). Чтобы убедиться в правильности вычислений и использова-
105
Рис. 33
ния формул, введем в ячейки H22:I22 формулу, возвращающую параметры линейной регрессии "=ЛИНЕЙН(B2:B21;A2:A21)". В диалоговом меню укажем область ячеек, содержащих х и у, и нажмем сочетание клавиш "Ctr+Shift+Enter" (это необходимо, если результатом
операции является не отдельное значение, а массив). В результате
получатся значения, совпадающие с вычисленными непосредственно
(см. рис. 33, H22:I22).
Пример 2. Создадим две последовательности случайных чисел xk,
yk ∈(-1, 1), k = 1, 2, ..., 20. Назовем рангом числа в последовательности
его номер после упорядочения этой последовательности (например,
среди чисел 22, -3, 17, 1 первое число будет иметь ранг 4, второе –
ранг 1, третье 3, четвертое 2, поскольку в порядке возрастания они расположатся, как -3, 1, 17, 27). Пусть rxk, ryk – ранги членов этих последовательностей (в порядке возрастания). Положим dk = rxk – ryk, k, и
ρ
вычислим S = ∑k (rxk – ryk)2, свертку ρ = ∑kxk∙y21-k и отношение ζ = S .
Запишем в ячейку А2 формулу "2*СЛЧИС()-1", протянем ее вправо на
одну позицию и вниз до строки 21 (х = ‹А2:А21›, у = ‹В2:В21›). Теперь
в ячейку С2 введем (из меню "вставка функции") формулу
"=РАНГ(A2;$A$2:$A$21;1)-РАНГ(B2;$B$2:$B$21;1)"
(ранг значения А2 в последовательности А2:А21 минус ранг В2 в последовательности В2:В21, ссылка на диапазон ячеек должна быть
абсолютной, единица в конце означает порядок по возрастанию) и протянем ее до С21. В С22 получим сумму квадратов содержимого
С2:С21 (формула "=СУММКВ(C2:C21)"). Свертка вычисляется чуть
хитрее: можно использовать формулу
"=A2*СМЕЩ(B$22;-СТРОКА(A1);0)",
106
по которой номер строки В$22 (фиксированный) изменяется (здесь –
уменьшается) на номер строки А1 (который при протягивании будет
увеличиваться). Введем эту формулу в D2 и протянем до D21, получив
тем самым последовательность xk∙y21-k, а в ячейке D22 посчитаем
свертку. Результат получается вставкой формулы "=D22/C22" в какуюнибудь ячейку.
Эти примеры показывают, как гибко и даже изящно позволяет
Excel обрабатывать информацию рабочего листа. Приведем еще
несколько примеров конкретных вычислений с использованием
надстроек "Подбор параметра" или "Поиск решения".
Пример 3. Пусть требуется решить кубическое уравнение
3
а3х +а2х2+а1х+а0=0. Оно имеет по меньшей мере один действительный
корень. Возьмем конкретно а = (2.2, 3, -22.4, 7.3)Т. Запишем эти числа
(в обратном порядке) в ячейки A5:D5, а в Е5 запишем текущее значение аргумента х = 0. В Е6 будем вычислять значение многочлена по
формуле "=((A5*E5+B5)*E5+C5)*E5+D5". Теперь обратимся к надстройке "подбор параметра", указав
изменяемую ячейку Е5 с результатом Е6, который должен быть равен нулю (рис. 34). Нажав "ОК", получим ‹Е5› = -0.24592, а в ячейке
Е6 значение многочлена -0.00097.
Если в Е5 сначала поместим х = 1,
то получим другой корень многочРис. 34
лена х = 0.424126. При начальном
значении х = 5 получим корень х = 2.890227. В Mcd встроенная
-0.246
функция polyroots(a) возвратит все три корня  0.424 .
 2.89 
Системы алгебраических уравнений удобнее решать с помощью
надстройки "Поиск решения".
Пример 4. Пусть нужно найти решение простой системы уравне2
2
x + y - 4 = 0,

ний  x∙y 1
В ячейки А1:В1 рабочего листа запишем единицы
x + y = 2 .
(начальные значения для поиска решения), в С1 введем формулу
"=А1*А1+В1*В1-4", в С2 – формулу "А1*В1/(А1+В1)-0.5". Вызовем
"Поиск решения", установив в целевой ячейке $C$1 значение 0 при
условии $C$2 = 0. После пуска в ячейках А1:В1 получим значения
1.88045 и 0.6811 соответственно. Выбрав другие начальные значения,
можно получить другие решения системы. Если система уравнений не
имеет точного действительного решения, можно в меню поиска мини-
107
мизировать сумму квадратов разностей левых и правых частей уравнений системы (см. следующий пример).
Пример 5 (более сложный). Пусть дана некоторая матрица С =
1
4
3
1
2
2
-3
2
3
-1
0
1
-2
2
3
2
1
-1
2
0
-2
4
1
-2
3
0
3
1
, записанная в ячейках G4:J10 рабочего листа. По-
строим матрицу А = СТС в ячейках K4:N8 по формуле (используя
функции транспонирования и умножения матриц)
"=МУМНОЖ(ТРАНСП(G4:J10);G4:J10)".
Найдем квадратный корень Х из матрицы А, решая уравнение Х2 = А.
Запишем в ячейки K9:N12 единичную матрицу (для начала поиска решения), в ячейки O4:R7 - квадрат матрицы Х по формуле
"=МУМНОЖ(K9:N12;K9:N12)",
в ячейках O9:R12 вычислим разность Δ =А-Х2 и в Р14 – сумму квадратов Δ: "=СУММКВ(O9:R12)". Будем изменять значения Х так, чтобы
минимизировать Δ, а матрица Х оставалась симметричной (это следует
указать в списке ограничений, см. рис. 35). Установив значение ячейки Р14 минимальным и
указав ссылки на изменяемые ячейки K9:N12
(здесь все ссылки должны быть абсолютными),
Рис. 35
запускаем процесс поиска решения. В результате получим матрицу
Х=
5.174964
-0.78936
4.022383
0.645791
-0.78936
3.98235
2.405643
0.854759
4.022383
2.405643
0.962722
0.326426
0.645791
0.854759
0.326426
6.224612
,
квадрат которой отличается от матрицы А лишь в пятом знаке после
запятой.
Пример 6. Решим следующую задачу линейного программирования: найти min x - y при условиях x – 4y ≤ -4, x – 2y ≤ 1, 5x – 2y ≤ 10,
10x – y ≥ 10,x + 2y = 10, x ≥ 0, y ≥ 0. Запишем в ячейки А1:В1 нули (в
качестве начальных значений х и у, в ‹С1› =А1-В1, в ячейки А2:Е2 –
108
значения левых частей ограничений, в А3:Е3 – правые части ограничений. Вызвав диалоговое окно "Поиск решений", определим в целевой
ячейке С1 минимальное значение, изменяя ячейки А1:В1. Внесем все
ограничения в виде А2≤A3, B2≤B3, C2≤C3, D2≥D3, E2=E3, A1≥0,
B1≥0. Программа находит решение х = 1.42857, у = 4.285715, минимум
равен -2.85714, первые три неравенства выполняются строго, последние два – равенства.
Аналогичным образом можно решать и транспортную, и другие
более сложные задачи.
Полезно отметить, что "Подбор параметра" является методом
Seek объекта Range() и может использоваться в программных модулях.
"Поиск решения" является надстройкой и работает лишь в диалоговом
режиме.
3. Работа в WORD
Среди большого числа существующих текстовых редакторов
(например, Open Office Word, Dolphin Text Editor, EuropeoSoft Alpine
Word, Ovis Pdf-Office, TEX, и др.) Word в системе Ms Office остается
достаточно популярным, поддерживая основные свойства и характеристики остальных редакторов. Ему уделяется достаточно внимания в
базовом курсе информатики, поэтому элементарные и общеизвестные
методы работы в Word упоминаются здесь достаточно конспективно.
Элементарная работа с текстом обеспечивается настраиваемым
меню, возможностью масштабирования, наличием горизонтальной и
вертикальной линеек, полосы прокрутки, строки состояния, выбором
режима из набора:
1) режим разметки (вид для печати),
2) обычный (для просмотра и редактирования),
3) режим структуры (отслеживание иерархии),
4) схема документа (со всеми заголовками),
5) Web-документ,
6) во весь экран,
7) многостраничный режим.
3.1. ОБЩЕЕ РЕДАКТИРОВАНИЕ
Общий вид документа существенно зависит от параметров
страницы (вид страницы, размер полей, и т.д.). Верхняя линейка позволяет автоматически устанавливать абзац, отступ, выступ как слева,
так и справа, а также разбивать документ на две части, допускающие
одновременное и независимое редактирование (см. рис. 36).
109
Кнопка
отступов
и выступов
Отступ первой строки
Отступ справа
Отступ слева
Кнопкаразделитель
Рис. 36. Верхняя линейка
Word допускает вставку произвольных символов из доступного списка
шрифтов размером от 8 до 72 пунктов (1pt = 0.352 mm), выделение
символов и текста как цветом, так и рамками. Возможна вставка
художественного текста (меню WordArt) и буквицы. Сам шрифт
может быть жирный, наклонный, зачеркнутый, подчеркнутый, надстрочный, подстрочный, и т.д., высоту и ширину знаков можно менять
независимо от выбранного шрифта. Отдельные части текста (с абзацем) могут быть маркированы (см. библиотеку маркеров) и (или) автоматически пронумерованы, разрешая многоуровневую структуру
списков. Например, в пределах одного и того же шрифта (Arial) можно
создать текст:
В н
я
ет
л
и
ст,
уходит
и
н
лето,
е е р т
ей с р б и ся…
и более сложный.
3.2. ВСТАВКИ
Здесь имеется в виду внедрение в текстовый документ "посторонних" объектов так, чтобы они стали "своими". Вставки обыкновенно
могут быть реализованы двумя способами: непосредственным внедрением в документ (например, изображения – в графический слой активного листа) и с помощью ссылки на содержащий объект источник. В
последнем случае это может быть ссылка на другую часть документа
(перекрестная ссылка) или на файл-источник (гиперссылка). В таком
случае объекты вставки могут редактироваться независимо от документа, кроме того, сам документ имеет меньший объем.
3.2.1. Графические объекты
Частым объектом вставки является надпись, которая помещается
в графический слой листа и не является элементом текста, но сама
предназначена для хранения текста, позволяет форматирование и
прочие действия с текстом, как элемент листа (но не допускает вставку
других графических объектов). Среди свойств надписи можно назвать
настройку границы, способы заливки, степень прозрачности, взаимодействие с окружающим текстом и с другими надписями. Надпись
хорошо совмещается с элементами графики (меню "Автофигуры",
110
"Группировка") и потому служит удобным элементои оформления
документа.
Элементы графики из меню "Рисование" ("Вставка" → "Фигуры") помещаются в графический слой листа просто выбором мышью
из соответствующего меню. Здесь есть надписи, стандартные геометрические фигуры, стрелки, линии, набор кривых линий (полиномиальные, Безье, произвольно рисованные, и т.д.), фигурные стрелки,
блок-схемы, выноски, звезды, и др. Рисунок, построенный из разнородных элементов графики может быть сгруппирован (стрелка
"выделение" → "группировать") в единый объект, который может
быть настроен, как любой другой внедренный элемент текста. Это делается совершенно аналогично тому, как описано в Excel.
Вставка математических символов и формул осуществляется преобразованием текстовых символов в графические объекты с помощью
специальных программ. По традиции Ms Office для этой цели снабжался надстройкой Ms Equation3. Для этой же цели можно использовать более современные пакеты, например, SciWriter, MathType
(см. рис. 37), и др (в Ms Office 2007 и старше это элемент меню).
Рис. 37. Меню программы MathType
Заметим, что вставленная таким образом формула является графическим элементом, а не элементом текста.
3.2.2. Поля и ключи
Этот раздел выходит за рамки программирования в каком-либо
языке и практически не представлен в учебной литературе, но важен в
плане информационных технологий. Инструмент полей и ключей
позволяет полнее и увереннее использовать богатые возможности
редактора Word. Ключи являются управляющими символами вспомогательных полей, которые используются в документах для хранения
изменяемых данных. В разной степени используются несколько
категорий полей, таких как Нумерация, Дата и Время, Связи и
Ссылки, Указатели, Формулы и др. Бóльшая часть полей –
своеобразные макрокоманды преобразования текста документа. Некоторые поля (такие как Нумерация, Ссылки и др.) фактически используются в меню "Параметры" настройки документа, другие можно
вводить явно для облегчения работы с документом. Здесь кратко коснемся категории полей Formula, включающая поля Symbol, Advance и
Eq. Поле вводится в фигурных скобках (меню "Вставка" → "Поле",
111
или комбинацией клавиш "Ctr+F9", фигурные скобки вводятся автоматически, не вручную), вначале указывается тип поля, затем (через
пробел) вводятся управляющие ключи (признак ключа – знак целого
деления "\"). Посмотреть на результат действия поля можно, нажав F9
или комбинацию "Shift+F9".
Поле Symbol используется для вставки символа в коде ANSI.
Его ключи:
\а – код рассматривается как знак ANSI,
\f "шрифт" – вставляет имя используемого шрифта,
\h – вставляется символ без изменения межстрочного интервала,
\sN – устанавливается размер знака в N пунктов,
\u – используется кодировка Unicod.
Пример 1. Поле {Symbol \83 \f "Symbol"\s40} помещает в текст
знак суммы (83 - ее код в шрифте "Symbol") высотой в 40 пунктов
(≈ 12 мм).
Поле Advance сдвигает следующую часть строки относительно
текущей позиции или в заданную абсолютную позицию. Ключи поля
\uN, \dN, \lN, \rN сдвигают текст на N позиций соответственно вверх,
вниз, влево и вправо относительно исходного положения. Ключ \xN
помещает текст на N пунктов от левого края, \yN сдвигает текст в
N-ю позицию вверх относительно текущей строки. Это поле бывает
полезно для выравнивания строк при вставке формул.
Поле Eq – аналог пакета Equation для вставки формул в текст.
Это поле имеет богатый набор ключей, позволяющий вставить в текст
практически любую формулу. Перечислим основные ключи.
\а( ) – вставляет в текст "матрицу" (прямоугольную таблицу), элементы которой, разделенные точкой с запятой, записываются
после ключа в круглых скобках. Есть добавочные ключи:
\al, \ac, \ar – выравнивание элементов матрицы по левому краю,
по центру или по правому краю,
\coN – матрица имеет N столбцов (по умолчанию – один),
\vsN – устанавливает интервал между строками N пунктов,
\hsN – устанавливает интервал между столбцами N пунктов.
\b( ) – помещает следующую в круглых скобках информацию в
скобки (круглые, квадратные, фигурные, прямые), при этом
величина скобок "подстраивается" под формулу. Подключи:
\lc\s – s символ левой скобки,
\rc\s - s символ правой скобки,
\bc\s – скобки s ставятся слева и справа.
\f(числитель; знаменатель) – вставка дроби.
\i(a; b; f) – вставляет знак определенного интеграла с пределами
a и b от функционального выражения f. Дополнительно:
\su – вместо интеграла вводится знак суммы,
112
\pr - вместо интеграла вводится знак произведения,
\in – пределы интегрирования помещаются справа от знака
интеграла (суммы),
\fc\s – вместо знака интеграла, суммы или произведения можно использовать произвольный символ s.
\l(список) – рассматривает список как один элемент.
\о(эл.1; эл.2) – размещает один элемент поверх другого. Ключи
\al, \ac, \ar выравнивают элементы по левому краю, по центру
или по правому краю соответственно.
\r(степ.; выр.) – записывает корень указанной степени из выражения (если степень не указана, корень квадратный).
\s( ) – выражение записывается как верхний или нижний индекс
(без изменения размера). Дополнительные ключи:
\upN, \doN – смещают следующий в скобках текст на N пунктов вверх или вниз,
\aiN, \diN – увеличивают интервал над или под строкой на N
пунктов.
\x( ) – помещает следующее в скобках выражение в рамку. Ключи
\to, \bo, \le, \ri – рисуют границу рамки сверху, снизу, слева
или справа соответственно.
Поля могут быть вложены друг в друга, ключи сохраняют шрифт
и размер символов, так что в формулах могут использоваться все прелести форматирования. Главное – не забывать о соответствии открывающих и закрывающих круглых скобок. Приведем несколько примеров использования полей разной сложности.
a b
Пример 2. Определитель  c d  можно создать с помощью поля


{eq \b\bc\|(\a\ac\co2\hs4(a;b;c;d))}, а систему уравнений
 ax2 + 2xy = y3
 3
можно записать с помощью поля
2
 x - (a + 1)(y - x) + 5 = 0
{eq \b\lc\{( \a\al(ax2 + 2xy = y3;x3 - (a2 + 1)(y - x) + 5 = 0))}.
n
Пример 3. Выражение
 u∙sin pi 
p  можно ввести с помощью

cos p∙i

U Si v +
i=1
поля:
{eq \s\up30(\i\fc\U (i = 1;n; \s\do26(\s\do6(Si )\b\bc\((\f(u∙sin pi;v + \f(p;cos
p∙i))))))}.
113
n+1
Пример 4. Выражение
2+
n
2+…+
2

можно ввести с по-
n корней
мощью поля { eq \x\to\le\bo\ri(\o(\r(n + 1;2 + \r(n;2 + … + \r(2)));\s\do10
(\o( ; \s\do8( n корней)))))}.
Пример 5. Этот довольно экзотический пример многократного
O
∞
наложения символов
∏
xn
xn +1
n=1
можно построить с помощью подходя-
щего подбора шрифтов и размеров, используя, например, поле
O
{eq \s\do20(\o\ac(
\o\ac(
∏
;\s\up18(\o\ac(\s\up4(\a\ac\vs30(∞;n = 1));
;\s\up4(\f(xn;xn +1)))))))}.
Еще одной особенностью полей является то, что в указанную позицию поля можно вставить не только элемент произвольного шрифта, но и произвольный рисунок. Это позволяет конструировать достаточно сложные комбинации формул и схем, что существенно расширяет возможности этого инструмента. Каждый созданный таким образом продукт является элементом текста документа, легко редактируется и подчиняется всем основным методам форматирования.
Отметим, что в практике обработки документов можно использовать более семидесяти различных полей (с ними можно ознакомиться
по мере необходимости). Среди оставшихся обратим внимание еще на
три. Это поле Hyperlink, в котором в кавычках указывается адрес
ссылки на текстовый или графический источник (ключи \l – элемент
документа для перехода, \m – добавляются координаты в схему сервера, \n – открывается конечный документ в новом окне и др.). Поле
XE "текст" [ключи], которое определяет текст и номер страницы для
вкючения в предметный указатель (ключи \b – указывает жирный
шрифт, \i – страницы записываются курсивом, \r – указывается диапазон страниц по закладке \t "текст"- вместо страниц указывается текст).
Поле Macrobutton позволяет щелчком мыши по выбранному тексту
запускать макрос. Структура поля такова: {Macrobutton имя (макро-
114
са) сообщение} (разделителями являются пробелы), где сообщением
является либо текст, остающийся на месте поля (в одной строке), либо
картинка-иконка. Это очень полезное поле для программируемого
изменения в документе.
Пример 6. Пусть в документе на щелчок мышкой по тексту "ТукТук!" появляется окно с налписью "Кто там?". Дадим макросу имя Rr.
Через меню "Разработчик" → "Макросы" → Имя "Rr" → "Создать"
заходим в VBA и записываем в тело макроса всего одну крманду:
MsgBox "Кто там?", vbQuestion,"". В документ вводим поле
{Macrobutton Rr Тук-тук!}, нажатие клавиши F9 возврашает нас в
текстовый режим – поле скрывается и в тексте остается только фраза
"Тук-тук!". Щелчок мышкой по ней запустит макрос и на экране
появится вопрос "Кто там?".
3.2.3. Закладки
Специфическим элементом вставки является закладка (меню
"Вставка" → "Ссылки" → "Закладка", в диалоговом окне вводится
имя и положение закладки). Закладка помечает место в документе, позволяет при необходимости легко отыскивать помеченные места, изменять текст в соответствии с какими-то условиями.
Пример. Рассмотрим следующий текст.
И наступит день…
Уважаемый г-н, настоящим сообщаю, что в ближайшее время Вас
ожидают замечательные и интересные события. Во-первых, Вы
почувствуете в себе необычайный душевный подъем, стремление
сделать как можно больше и как можно лучше. Во-вторых, пройдет
совсем небольшое время (может быть 2 месяца) и Вы сможете
насладиться увлекательным путешествием в свое прошлое и будущее.
Великолепные горизонты откроются перед Вами, и многие будут
восхищаться Вами и даже завидовать Вам.
Настроим текст в соответствии с вводимой информацией. Заголовку
"И наступит день..." назначим макрос Profet, вставив поле
{Macrobutton Profet И наступит день...}. Выделим часть слова
"Уважа" и пометим ее меткой "one", выделив слово "месяца", пометим
его меткой "two". Далее, через меню "Разработчик" → "Макросы" →
Имя "Profet" → "Создать" заходим в VBA и записываем в тело макроса
код:
Sub Profet()
′макрос, изменяющий текст, ориентируясь на закладки
′
Dim t As String, s As String * 1, r As Byte
Randomize Timer
t = InputBox("Введите свою фамилию", "Информация к тексту", "")
If t = "" Then Exit Sub
'***ничего не меняется, если ввод пустой
115
'***анализ последней буквы фамилии и выбор случайного числа
s = Right(t, 1): r = 1 + 50 * Rnd
Selection.GoTo what:=wdGoToBookmark, Name:="one" '***переход к первой метке
With ActiveDocument.Bookmarks
'***метка найдена
.DefaultSorting = wdSortByName
.ShowHidden = True
With Selection
If (s = "а") Or (s = "я") Then
'***если фамилия кончается на а-я (женская)
.MoveRight unit:=wdCharacter, Count:=3
'***сдвиг на 3 позиции вправо
.Delete unit:=wdCharacter, Count:=2
'***удаляем два символа
.TypeText Text:="ая"
'***вставляем текст: ая
.MoveRight unit:=wdCharacter, Count:=3
'***сдвиг вправо на 3 позиции
.Delete unit:=wdCharacter, Count:=1
'***удаляем один символ
.TypeText Text:="жа " & t
'***вводим текст: жа и фамилию
Else
.MoveRight unit:=wdCharacter, Count:=9
'***пропускаем 9 позиций
.TypeText Text:=" " & t
'***и вставляем фамилию (мужскую)
End If
End With
End With
Selection.GoTo what:=wdGoToBookmark, Name:="two" '***переход ко второй метке
With ActiveDocument.Bookmarks
'***метка найдена
.DefaultSorting = wdSortByName
.ShowHidden = True
With Selection
.MoveLeft unit:=wdCharacter, Count:=2
'***сдвиг влево на 2 позиции,
.TypeBackspace
'***со стиранием символов
.TypeText Text:=Format(r)
'***вставка случайного числа
End With
End With
End Sub .
Пусть (после щелчка по заголовку) введена фамилия "Суркова". Запущенный макрос изменит текст следующим образом.
Уважаемая г-жа Суркова, настоящим сообщаю, что в ближайшее
время Вас ожидают замечательные и интересные события. Во-первых,
Вы почувствуете в себе необычайный душевный подъем, стремление
сделать как можно больше и как можно лучше. Во-вторых, пройдет
совсем небольшое время (может быть 4 месяца) и Вы сможете
насладиться увлекательным путешествием в свое прошлое и будущее.
Великолепные горизонты откроются перед Вами, и многие будут
восхищаться Вами и даже завидовать Вам.
3.3. ТАБЛИЦЫ
Таблицы в документ вставляются, в основном, двумя способами:
рисованием и по шаблону (меню "Вставка" → "Таблица"). Возможно
копирование таблиц Excel. В каждой ячейке таблицы текст может
быть форматирован независимо от остальных. Щелкнув мышкой (правой кнопкой) по левому верхнему углу таблицы (курсор принимает
116
вид крестика), или в меню "Макет", можно вызвать меню различных
преобразований таблицы (вставка и удаление строк, столбцов, разбиение или объединение ячеек, вставка подтаблиц, и т.д.). Выбрав в
нем "Свойства таблицы", можно, далее, выбрать стиль оформления
таблицы, настроить границы ее и отдельных ячеек, организовать
заливку выбранным цветом, настроить ее положение по отношению к
окружающему тексту.
Таблица, как элемент рабочего листа, может играть роль контейнера внедренных элементов (например, рисунков, формул, и др.), а
также помогает в оформлении текстовых элементов документа.
Например, если желательно текст страницы оформить в виде четырех
(приблизительно) одинаковых кусков в два ряда (выравнивание в этом
случае весьма непросто), то можно вставить таблицу из двух строк и
двух столбцов, вписать в нее необходимый текст, а затем в свойствах
таблицы ("Границы и линии" или меню "Конструктор") убрать все
границы. В каждой ячейке можно выполнить необходимое выравнивание. В результате получим требуемое оформление текста без дополнительных усилий.
Ячейки таблицы допускают вставку формул для простейшего автоматического расчета: "Вставка" → "Формула" или "Работа с таблицами" → "Макет"→ "Данные" → "Формула fx". Набор возможных функций можно найти в диалоговом окне вставки (см. рис. 38).
Функции обрабатывают содержимое
вышележащих ячеек таблицы (аргумент функции Above) или расположенных левее (аргумент Left). При
изменении табличных данных поля
формул следует обновлять.
Пример 1. В табл. 9 введем в последней строке формулы: во втором
Рис. 38
столбце Sum(Above), в 2, 4, 5 Average(Above). В последний столбец введем формулы , Product(Left),
Product(Left) и Sum(Above). Результат вычислений – в табл. 9.
Таблица 9
Наим.
товара
Пальто
Сапоги
Всего
Кол-во
цена
4
9
13
6800
4200
5500
Скидка
поставщика
0,9
0,75
0,83
Наценка
продажи
1,8
2,1
1,95
Сумма
44064
59535
103599
117
Более надежная (хотя, возможно, не более простая) обработка
табличных данных может быть выполнена программным способом (с
помощью макросов).
Пример 2. Модель авторынка. Построим таблицу для пяти марок
автомобилей шести возрастных категорий с указанием цены нового
автомобиля. Будем считать, что с возрастом х лет цена изменяется в
1  3x2  ax3
k(x) = 1 + sin
раз (a = 0.0003). Количество автомоби2 35+2x3 1+ax3
лей на базе случайно, но не более 10 штук каждой марки. Следует
посчитать суммарную стоимость авто каждой марки. Построим
таблицу 15×7, заполним вторую строку и первый столбец таблицы.
Для указания года выпуска объединим две соседние ячейки в одну.
Заголовку таблицы "Авторынок" назначим макрос Auto: {Macrobutton
Auto Авторынок}. Код макроса запишем в виде (комментарии помогут разобраться в логике программы, ссылка на ячейку таблицы –
Cell(i, j), индексация начинается с единицы):
Sub Auto()
' Auto Macros
Dim i As Byte, j As Byte, k As Single, x As Single, p As Integer
Dim price() As Integer
'***массив цен
Const m As Byte = 15
'***общее число строк в таблице
Const n As Byte = 7
'***число столбцов таблицы
Const a As Single = 0.0003
ReDim price(3 To n)
'***нумерация ячеек цен начинаеися с 3
Randomize Timer
'***подготовка генерации случайных чисел
With ActiveDocument.Tables(1)
'***следует указывать номер рабочей таблицы
For j = 3 To n
'***перебор строк
.Cell(2, j - 1).Select
'***выбор ячейки: во второй строке на 1 ячейку меньше
price(j) = Val(Selection.Text)
'***считывание цен из таблицы
Next
For i = 3 To m - 1
'***подготовка информации по строкам
If i And 1 Then
.Cell(i, 1).Select '***выбор ячейки: при оъединении остается первый индекс
p = Val(Selection.Text)
'***считывание года выпуска
End If
For j = 3 To n
.Cell(i, j).Select
'***выбор ячейки для записи информации
With Selection
.Cut
'***очистка содержимого (это не делается автоматически!)
If i And 1 Then
.InsertAfter Str(Int(11 * Rnd))
'***случайное число в нечетную ячейку
Else
x = 2012 - p: k = x ^ 3
'***вычисление множителя к(х)
k = 1 + 0.5 * Sin(3 * x ^ 2 / (35 + 2 * k)) - a * k / (1 + a * k)
.InsertAfter Str(k * price(j))
'***запись цены в четную ячейку
End If
End With
Next
Next
118
For j = 3 To n
k=0
'***подсчет окончательной суммы (по столбцам)
For i = 3 To m - 1 Step 2
.Cell(i, j).Select
'***выбор ячейки
p = Val(Selection.Text)
'***считывание содержимого
.Cell(i + 1, j).Select
x = Val(Selection.Text)
'***считывание цены
k=k+p*x
'***суммирование
Next
.Cell(m, j - 1).Select
'***выор ячейки для записи суммы
With Selection
.Cut: .InsertAfter Str(k)
'***очистка и запись результата
End With
Next: .Cell(1, 1).Select
End With
End Sub .
Окончательный результат – см. табл. 10.
Таблица 10. Авторынок
Марка
автомобиля
Цена за новую
(тыс. руб.)
Шт.
2010
Цена
Шт.
2005
Цена
Шт.
2000
Цена
Шт.
1995
Цена
Шт.
1990
Цена
Шт.
1980
Цена
ИТОГО
...
...
...
....
...
500
1250
399
1800
880
4
557.0851
1
503.9687
10
360.1518
8
224.0623
9
136.2109
10
57.87456
9930.97
2
1392.713
8
1259.922
4
900.3795
8
560.1556
5
340.5273
0
144.6864
22650.2
9
444.5539
2
402.167
6
287.4011
0
178.8017
9
108.6963
8
46.1839
7877.464
2
2005.506
1
1814.287
10
1296.547
10
806.6241
9
490.3593
3
208.3484
31895.29
1
980.4698
0
886.9849
5
633.8672
9
394.3495
9
239.7312
10
101.8592
10875.12
В общем, обращение с ячейками таблицы Word, как носителями
информации, мало чем отличается от ячеек Excel. Прежде всего,
ячейка (Cell) в Word – это дочерний элемент таблицы (Tables),
которая, в свою очередь, является дочерним элементом документа
(ActiveDocument) – эта иерархия должна учитываться при программировании. Далее, все изменения возможны только в активной ячейке
(поэтому ее следует выбирать – Select). Наконец, при записи в ячейку
(текстовой информации) прежнее содержание не исчезает автоматически, его можно убрать (Cut) или к нему добавить текст (TypeText,
InsertBefore или InsertAfter). Содержимое ячейки возвращается
свойством Text. Кроме того, русификация приложения имеет свою
отрицательную сторону: при преобразовании типов число
строка
функция Format не преобразует десятичную точку в запятую (и
119
наоборот), что нарушает вычисления, в этой ситуации лучше использовать функцию Str (это замечание относится и к Excel). При работе с
большими таблицами использование макросов для автоматических
расчетов, безусловно, предпочтительнее вставки формул.
В ячейки таблицы можно вставлять поля формул непосредственно
в кодах макроса. Например, для вставки в выбранную ячейку таблицы
поля {eq \...} достаточно набрать код
With Selection
.Fields.Add Range := Selection.Range, Type := wdFieldEmpty, _
PreserveFormatting := False
'***ввод фигурных скобок поля
.Delete Unit := wdCharacter, Count := 1
.TypeBackspace
'***удаление лишних пробелов
.TypeText "eq \..."
'***ввод формулы
.Fields.Update
'***преобразование к формату текста
End With .
Если в формуле (или любом вводимом тексте) встречается символ, отсутствующий в раскладке клавиатуры, его можно вставить в текст,
указав код в функции Chrw(код). Код можно узнать в таблице символов меню "Вставка" →"Символ". Свойства шрифта, такие как верхний
или нижний индексы, наклон,подчеркивание, и др., включаются прямым указанием свойства (через точку) и (если необходимо) присваиванием встроенной константы wdToggle (включить). Например, такой
текст "log 2x-1 x2+3" в выбранную ячейку можно ввести кодом:
With Selection
.TypeText "log"
.Font.Subscript = wdToggle
.TypeText " 2x-1 "
.Font.Subscript = wdToggle
.TypeText "x"
.Font.Superscript = wdToggle
.TypeText "2"
.Font.Superscript = wdToggle
.TypeText "+3"
End With .
'***включен нижний индекс
'***выключен нижний индекс
'***включен верхний индекс
'***выключен верхний индекс
Пример 3. Пусть щелчком мыши по заголовку таблицы "Тест" в
первой ячейке таблицы случайным образом появляется неравенство
для решения (решение предлагается записать в другую ячейку) из заx2-3x+2
данного набора формул:
> 0, sin(2x)tg(x) > 1, 4log2x-1x < x,
x-3
x2-1
< 0 . В поле Macrobutton назначим заголовку таблицы
x3-4x2+2x+1
макрос Test, в котором вырабатывается целое случайное число k: 0 < k
< 5. В блоке:
120
With selection
Select Case k
Case 1: ‹вставка первой формулы›
...
Case 4: ‹вставка четвертой формулы›
End Select
End With
в зависимости от выбранного числа в ячейку таблицы вставляется то
или иное неравенство для решения.
Все это может выглядеть достаточно утомительным, если не
учитывать, что, во-первых, во всех этих кодах просматривается очень
простая логика, во-вторых, как отмечено выше, каждый пакет Ms
Office допускает автоматическую запись макроса, который легко
можно приспособить под свою конкретную задачу.
3.4. ГРАФИКА
Графика реализуется в Word так же, как в Excel, за тем исключением, что выбор типа диаграммы, в общем, затруднителен. Этот
выбор, в сущности, определяется несколько урезанными возможностями Excel, но обогащен возможностями SmartArt.
С помощью автофигур (меню "Рисование", "Автофигуры") изображение графиков значительно проще. Выполняется это так же, как в
Excel. Программирование графики осуществляется теми же кодами,
что и в Excel, заменяя объект ActiveSheet объектом ActiveDocument, и
выбор цвета линии реализуется методом .ForeColor.RGB =
RGB(a,b,c), где a, b, c – целые числа из промежутка [0, 255],
указывающие на степень присутствия красного, зеленого, синего в
результирующем цвете.
Для построения графиков в Word используется та же техника, что
и в Excel. Подготовить таблицу данных для графического представления несложно описанными выше способами. Можно сделать это и с
помощью кода (например, для таблицы 2×12):
ActiveDocument.Tables.Add Range:=Selection.Range, NumRows:=2, _
NumColumns:= 12, DefaultTableBehavior:=wdWord9TableBehavior, _
AutoFitBehavior:= wdAutoFitWindow
With Selection.Tables(1)
If .Style <> "Сетка таблицы" Then
.Style = "Сетка таблицы"
End If
.ApplyStyleHeadingRows = True
.ApplyStyleLastRow = True
.ApplyStyleFirstColumn = True
.ApplyStyleLastColumn = True
End With .
121
Приведем для сравнения пример построения графика функции f(x) =
∞
[ln(n)]
2n - 1
(-1)
n! x
∑ 2n
, разобранный в п. 2.4, с помощью макроса. В реn = 1 3n П (1 + kx)
k=1
дакторе VBA вставим модуль, в который введем код вычисления
функции:
Function f(x As Single) As Single
Dim x2 As Double, n As Integer, mn As Long, q As Double
Dim k As Integer, sum As Double
Const eps As Double = 0.00001
x2 = x * x: n = 1: mn = 3: q = x / (3 * (1 + x)): sum = q
While Abs(q) >= eps
n = n + 1: mn = 9 * mn: q = q * x2 * Sqr(n) / (mn * (1 + n * x))
If Int(Log(n)) And 1 Then k = -1 Else k = 1
sum = sum + k * q
Wend: f = sum
End Function .
Используя предыдущий код, построим макрос создания и заполнения
таблицы значений функции:
Sub T()
Dim i As Byte, x As Single, y As Single
ActiveDocument.Tables.Add Range:=Selection.Range, NumRows:=2, _
NumColumns:=12, DefaultTableBehavior:=wdWord9TableBehavior, _
AutoFitBehavior:=wdAutoFitWindow
With Selection.Tables(1)
If .Style <> "Сетка таблицы" Then
.Style = "Сетка таблицы"
End If
'***рисование таблицы
.ApplyStyleHeadingRows = True
.ApplyStyleLastRow = True
.ApplyStyleFirstColumn = True
.ApplyStyleLastColumn = True
.Cell(1, 1).Select
With Selection
.Cut: .InsertAfter "X:"
End With
.Cell(2, 1).Select
With Selection
.Cut: .InsertAfter "Y:"
End With
For i=2 to 12 '***вычисление значений функции и заполнение таблицы
x = i – 2: y = f(x)
.Cell(1, i).Select
With Selection
.Cut: .InsertAfter Str(x)
End With
.Cell(2, i).Select
With Selection
.Cut: .InsertAfter Str(y)
End With
Next
122
End With
End Sub .
Далее, создадим макрос построения графика:
Sub Graph()
Dim i As Integer, m As Integer, n As Integer, j As Integer
Dim a As Single, b As Single, h As Single, x() As Single
Dim y() As Single, xm As Single, ym As Single, z As Single
Const eps = 0.01
n = 10: ReDim x(n), y(n)
With ActiveDocument.Tables(1)
'***чтение из таблицы
For i = 0 To n
.Cell(1, i+2).Select: x(i) = Val(Selection.Text)
'***значения х
.Cell(2, i+2).Select: y(i) = Val(Selection.Text)
'***значения у
If y(i) > ym Then ym = y(i) '***максимальное значение функции
Next
End With
a = 0: b = 10: h = (b - a) / n
xm = 300 / (b - a): ym = 200 / ym
'***масштаб по х и по у
'**** Рисование стрелок (осей координат) ****
With ActiveDocument.Shapes
.AddLine(150, 650, 480, 650).Select
'***горизонтальная линия
With Selection.ShapeRange
.Line.EndArrowheadStyle = msoArrowheadTriangle '***стрелка
.Line.EndArrowheadLength = msoArrowheadLengthMedium
End With
.AddLine(150, 650, 150, 430).Select
'***вертикальная линия
With Selection.ShapeRange
.Line.EndArrowheadStyle = msoArrowheadTriangle '***стрелка
.Line.EndArrowheadLength = msoArrowheadLengthMedium
End With
'**** Рисование линии графика ****
a = 150: b = 650 - ym * y(0): h = x(0)
With .BuildFreeform(msoEditingAuto, a, b)
'***начальная точка
For i = 1 To n: a = 150 + xm * (x(i) - h): b = 650 - ym * y(i)
.AddNodes msoSegmentCurve, msoEditingAuto, a, b
Next
.ConvertToShape.Select
'***линия построена
End With
End With
With Selection.ShapeRange.Line
.Weight = 2.5
'***толщина линии
.Style = msoLineSingle
'***стиль – одинарная линия
.ForeColor.SchemeColor = RGB(255,0,0)
'***красный цвет
.Visible = msoTrue
End With
End Sub .
В результате получим график, совпадающий (по форме) с графиком на
рис. 31.
123
Как уже отмечено выше, Word допускает вставку графических
объектов почти любой природы, так что проблем с воспроизведением
разного рода фигур и диаграмм не возникает.
4. Базы данных
Несмотря на то, что Visul Basic хорошо приспособлен для работы
с массивами разнородных данных, имеется много других средств для
квалифицированного выполнения такой работы. Совокупность данных, связанных многосторонними отношениями, называется базой
данных (БД). Если эта база отражает специфику какой-то части интеллектуальной деятельности человека, то иногда эту базу называют базой знаний (БЗ). Приведем краткий обзор сведений по этой теме.
1. Определение:
БД - структурированная система тематически связанных сведений
(данных).
2. Структура БД :
а) иерархическая (определена степень подчиненности, например,
библиотечный каталог, файловая система),
б) реляционная (определен уровень отношений между элементами
БД, например, совокупность знаний с системой межпредметных
связей),
в) смешанная (существует и иерархия, и связь, как, например, в генеалогии).
3. Средства работы с БД:
а) MS EXCEL, б) Visual BASIC, в) MS ACSESS.
На рис. 39 показан пример иерархической организации БД.
Рис. 39. Иерархическая структура БД
124
Реляционную базу данных можно представить системой отношений
(см. рис. 40).
Рис. 40. Пример реляционной структуры БД
Технологически всякая база данных представляет собой совокупность
взаимосвязанных объектов, таких как
1. таблицы данных, их свойств и отношений.
2. запросы, необходимые для извлечения данных из таблиц и предоставления их пользователю в удобном виде.
3. формы – удобное средство для ввода данных, заполнения полей
таблиц, бланков, контейнеры для различных элементов управления.
4. отчеты, в которых реализуется специальная выборка из БД и организация выборки (вместе с необходимой служебной информацией) в надлежащем виде.
5. страницы, осуществляющие связь Web-страниц пользователя с
БД, остающейся на сервере.
6. модули и макросы, создаваемые средствами VBA для реализации
функций управления БД.
4. Средства создания БД:
1. Ручные – разработка объектов в режиме конструктора (напр. таблицы, запросы)
2. Автоматизированные – разработка с помощью программ- мастеров (напр. формы, отчеты)
3. Автоматические – средства ускоренной разработки простейших
объектов (шаблоны).
125
В Excel возможность устанавливать связи между ячейками и группами ячеек (с помощью меню "Hyperlink") позволяет создавать несложные базы данных. Эффективное использование VBA помогает осуществлять управление БД непосредственно в Excel. На рис. 41 приведен
пример конструкции генеалогического дерева в рабочем листе.
Рис. 41
Аналогичная структура, созданная в Visual Basic, безусловно, более
привлекательна и удобна (см. рис. 42).
Рис. 42
126
Для профессионального создания БД и работы с ними можно
использовать пакет Access, входящий в состав Ms Office. Этот пакет
имеет удобный интерфейс, подробную систему подсказок и мастерокон, позволяющую пользователю быстро овладеть навыками работы
с БД. На рис. 43 приведен пример учебной БД в пакете Access.
Рис. 43
Ms Access используется в качестве:
1. инструмента для создания БД,
2. платформы создания настольных приложений и приложений
клиент/сервер уровня подразделения или предприятия,
3. автономной системы управления базами данных (СУБД) для
настольных систем,
4. СУБД для файлового сервера,
5. интерфейсного клиента для связи с серверными СУБД (например,
с MS SQL Server, который не является составной частью MS
Office и устанавливается отдельно).
Работа с таблицами в Ms Access:
1. Создание таблиц.
2. Определение ключевых полей. Это могут быть
а) последовательные числа (как при автозаполнении),
б) числа, вводимые пользователем,
в) коды (сочетания чисел и букв, вводимые пользователем).
3. Создание информационных полей типа
а) text (для хранения символьной информации),
б) memo (для больших текстовых материалов),
в) number (для числовой информации),
г) счетчик (Long Integer),
127
д) логический (типа ДА/НЕТ),
е) объект (внедренные рисунки, файлы, и т.д.)
ж) гиперссылка (для работы в сети).
4. Создание межтабличных связей типа
а) один к одному,
б) один ко многим,
в) многие к одному,
г) многие ко многим.
(связь осуществляется по схеме: "перенести - и – оставить").
Технически:
1. Создание таблиц удобно выполнять в режиме конструктора.
2. Выделить ключевое поле можно правым щелчком мыши
(выбрав соответствующий пункт всплывающего меню).
3. Тип информационного поля выбирается из раскрывающегося
списка справа.
4. Межтабличные связи создаются по цепочке: Сервис
Схема
данных
вставка таблицы (для связи с выбранной)
перетаскивание (левой) мышью связи из поля одной таблицы к
полю другой (“перенести - и - оставить”).
Работа с запросами (язык SQL)
1. Упорядочение записей в результирующей таблице.
2. Управление отображением данных.
3. Использование условий отбора.
4. Запросы на выборку.
5. Запросы с параметром.
6. Запросы на изменение.
7. Перекрестные запросы.
8. Специфические SQL-запросы к серверу БД.
Технически:
1. Запросы удобно создавать с помощью конструктора, добавляя
по необходимости интересующие данные таблиц (таблицы и
поля).
2. Условия отбора данных определяются по вычислимым полям
таблиц с возможным использованием арифметических операций
и символов сравнения. Можно в соответствующую строку в квадратных скобках ввести текстовую информацию о выборе данного параметра (например, [укажите максимальное значение]).
Можно также использовать оператор LIKE.
3. В меню ВИД можно выбрать команду Групповые операции,
помогающие в анализе всех данных выбранной категории.
4. Используя схему данных (связи таблиц) можно создавать
128
многотабличные запросы.
5. В режиме конструктора для облегчения обработки запросов
полезно индексировать некоторые поля, вызвав соответствующее меню правым щелчком мыши в верхней части таблицы.
6. После создания запроса следует запустить обработку (RUN).
Работа с формами (мастер!) сводится, в основном, к выбору структуры формы, ее дизайна и используемых элементов управления.
Упражнение. Создайте в качестве базы данных свое генеалогическое дерево.
5. Гипертекстовая разметка
Вся оформительская "кухня" докуметнов Word остается, так сказать "за кадром" – готовый документ в DOS просмотреть и отредактировать невозможно. Такие документы не воспринимаются в Intrnet.
Для формирования Web-документов используется так называемый
язык гипертекстовой разметки HTML (HyperText Markup Language).
Созданный с помощью этого языка документ (он имеет формат с расширением .htm) представляет собой ASCI I-файл, доступный для просмотра и редактирования в любом редакторе текстов. В принципе
пользователю и не обязательно знать HTML, так как аналогично Word
есть и другие редакторы (например, Web-Page, Front-Page), позволяющие с помощью достаточно подробного меню создать вполне сносный
Web-документ. Тем не менее, знание помогает использовать многие
скрытые возможности HTML-форматирования.
Язык HTML достаточно простой. Он построен по принципу
"операторных скобок", снабженных некоторыми дополнительными атрибутами: почти всякая операция является "открывающей скобкой"
участка документа и имеет свою пару – "закрывающую скобку". Такие
операторы называются тэгами (tag – ярлык, бирка) и оформляются
всегда в угловых скобках. Например, пара тэгов < Html> </ Html> (закрывающий тэг всегда начинается с косой черты) ограничивает область документа. Парный тэг <Title> </Title> определяет название
документа, а пара <Body> </ Body> ограничивает тело (содержимое)
документа. Этот тэг имеет атрибут BGColor (цвет фона). Например,
пара <Body BGColor=Pink> </ Body> организует розовый фон
документа. Дальше будет указываться лишь "открывающий" тэг с пометкой "парный", если есть соответствующий "закрывающий".
129
5.1. ОСНОВНЫЕ ТЭГИ HTML
Перечислим базовые тэги языка с коротими комментариями.
<P> (парный) определяет параграф (текст с новой строки). Закрывающий тэг добавляет пустую строку. Имеет атрибут выравнивания Align = Left, Center или Right. Существует и парный тэг
<Center> для выравнивания текста.
<Hn> (парный) определяет заголовок порядка n = 1 … 6. Заголовок
порядка 1 записывается самым крупным шрифтом, порядка 6 –
самым мелким.
<Font> (парный) устанавливает шрифт текста. Имеет атрибуты Face =
"название шрифта", Color = цвет, Size = размер (высота в пунктах).
<BR> - принудительное прерывание текста (переход на новую строку).
<Pre> (парный) определяет текст в исходном формате (т. е. со всеми
знаками форматирования, типом и размером шрифта и т. д.).
Некоторые символы, являющиеся знаками HTML, должны
быть заменены, например, символы <, >, & следует заменять
на &lt, &gt, &amp соответственно. Парные тэги < B>, <I>,
<U>, <Sub>, <Sup> выделяют текст жирным шрифтом, наклонным, подчеркнутым, надстрочным и подстрочным соответственно.
Непарный тэг <!- - комментарий--> вводит комментарий.
Для создания списков используются тэги:
<UL> (парный) организует простой список, каждый элемент списка
предваряется (непарным) тэгом <LI>,
<OL> (парный) организует нумерованный список вместе с тэгом <LI>,
<DL> (парный) организует список с определениями (каждый пункт
списка подкрепляется определяющей строкой), каждый элемент
списка предваряется непарным тэгом <DT>, а каждый элемент
определений (пояснений) – непарным тэгом <DD>.
Непарный тэг <HR> с атрибутами size = размер, width = ширина, align = выравнивание, color = цвет (не везде, правда, эти атрибуты
реализованы) определяет полосу-разделитель в документе.
Графические элементы могут быть вставлены в текст тэгом
<Image SRC = "адрес источника"> с атрибутами Align = Top, Middle
или Bottom (относительно предыдущего текста). Можно также
указывать размер рисунка: width = ширина, height = высота в
пикселях или в процентах от соответствующего размера экрана.
Адрес источника должен соответствовать серверу ресурсов, т.
е. если это Web-адрес (URL), то ссылка должна иметь вид
"http: //www. …", если это файл из местного каталога, то ссылка
130
"file:///C:/ ...‹полный путь›".
Вообще же ссылка на произвольный адрес (рисунка, текста,
мультимедиа и т. д.) осуществляется тэгом <a Href="адрес ссылки">
в паре с тэгом </a>. Между ними располагается текст, или рисунок,
или какой-нибудь другой элемент документа. При просмотре документа этот элемент выделен цветом (шрифта или границы) и щелчок
мышкой по нему реализует указанную ссылку. В некоторых случаях
ссылка является атрибутом тэга. Например, если необходимо рисунок,
расположенный в местном каталоге по адресу C:/Temp/Logos.jpg, сделать фоном документа, то ссылку на него можно включить в тэг
<body background="file: /// c:/temp/Logos.jpg" bgpropertiex="fixed">.
Заметим еще, что HTML "не любит" кириллицу и в большинстве
случаев заменяет ее знаки символами вставки: &#n, где n – код соответствующего символа в таблице используемого шрифта.
5.2. ФОРМАТИРОВАНИЕ ТАБЛИЦ
Таблицы создаются парным тэгом <table>, который имеет много
организационных атрибутов. Перечислим некоторые.
Align= Left, Center, Right выравнивает таблицу.
Border=n определяет границу в n пунктов. Если этот атрибут не
указан, либо n = 0, граница таблицы при просмотре отсутствует.
Width=n определяет ширину таблицы в пикселях, если n натуральное число, либо как доля ширины экрана, если n – в процентах.
Указывать размеры в процентах бывает удобнее при различной
настройке экрана (относительные размеры сохраняются).
Cellspacing=n определяет расстояние между ячейками таблицы (по
умолчанию n = 1 пикселу).
BGColor= цвет фона таблицы, BorderColor= цвет границы.
Граница таблицы может выглядеть объемной благодаря различной раскраске "светлой" и "темной" частей границы.
Таблица может иметь заголовок, определяемый парным тэгом
<caption> ("контейнер заголовка"). Конструкция
<caption> текст заголовка </caption>
должна располагаться между <table> и </table>.
Кадый ряд (строка) таблицы описывается парным тэгом <TR>.
Пару <TR> … </TR> нужно указывать столько раз, сколько строк в
таблице. Внутри этой пары перечисляются все ячейки ряда парными
тэгами <TD> …</TD>. Основные атрибуты ячеек: Width (ширина) и
Height (высота). Каждая ячейка может иметь свой цвет фона, свой
шрифт и т. д. Более того, поскольку определяющие тэги суть просто
операторные скобки, то между ними можно вставить любую мысли-
131
мую конструкцию, определяемую аналогичными скобками. Таким образом, содержимым ячейки таблицы может быть произвольный текст,
рисунок, ссылка на другой документ, другая таблица и т. д.
Внутри пары <TR> …</TR> можно поместить заголовок ряда:
<TH> текст заголовка </TH>. Как и в Word конструирование таблицы
помогает аккуратнее расположить и оформить текст, особенно если он
включает нетекстовые элементы (например, рисунки, графику).
Пример. Web-страничку (рис. 44), содержащую заголовки, различные шрифты, таблицу и рисунок,
Рис. 44
можно создать следующим HTML-кодом (рисунок и текст вопроса
вставлены в отдельную таблицу):
<html>
<head>
<meta http-equiv="Content-Type" content="text/html; charset=windows1252">
<title>ОПРЕДЕЛЕН&#
1048;Я</title>
<style type=text/css>
body {text-color:blue;background:#FFFF99}
h1 {color:red}
dt {color:blue;text-decoration:underline}
caption {color:brown}
th {color:brown}
</style>
</head>
<body>
<h1
align=left><u>ОПРЕДЕЛЕ&
#1053;ИЯ</u></h1>
132
<dl compact>
<dt>ТАКСОНОМИ&#10
71;</dt>
<dd>принцип
систематиз&
#1072;ции</dd>
<dt>ПРИМИТИВ</dt>
<dd>система
взглядов
без должной
детализаци&
#1080;</dd>
</dl>
<table width=75% align=center bgcolor=#CCFF99 border=4 rules=all>
<caption
align=center><b>ДРЕВНЯЯ
ТАКСОНОМИЯ<
/b></caption>
<tr>
<th>Звери</th>
<td>Плотоядны&#10
77;</td>
<td>Травоядны&#10
77;</td>
<td>Морские</td>
</tr>
<tr>
<th>Птицы</th>
<td>Летающие</td>
<td>Бегающие</td>
<td>Плавающие</td
>
</tr>
<tr>
<th>Рыбы</th><td>Наст&#
1086;ящие</td><td>Кост&
#1080;стые</td><td>Двоя
кодышашие</td>
</tr>
<tr>
<th>Гады</th>
<td>Крокодилы</td
>
<td>Черепахи</td>
<td>Змеи</td>
</tr>
</table>
<table width=80% height=30%>
<tr height=30%>
<td width=40%><img src=BIGBIRD.BMP align=right></td>
<td width=40%><font size="18" color=#FF0066>А
это кто повашему?</font></td>
</tr>
</table>
</body>
</html>
Здесь вся кириллица заменена кодами.
133
5.3. ФРЕЙМЫ
Язык HTML позволяет создать еще одну отличительную конструкцию: объединить в одном документе несколько документов, сохранив
при этом возможность их совместного и раздельного просмотра, включая взаимные и перекрестные ссылки. Фрейм (frame – рамка) – это
способ разбиения просматриваемой страницы на прямоугольные части. Способ задается парным тэгом <FrameSet>, который имеет атрибут Cols="m, n" (где m и n - ширина каждой из двух вертикальных
частей экрана) или Rows="m, n" (если экран разбивается на две горизонтальные части). Полезно иметь в виду, что сумма m + n должна
быть равна соответствующему размеру экрана, поэтому эти размеры
лучше указывать в процентах. Можно указать атрибут, например,
Cols="25%,*,2*", который означает, что экран разбивается на три части: первая занимает 25% экрана, вторая и третья – остальные 75%,
причем третья занимает в два раза больше места, чем вторая. Атрибуты Border=n и BorderColor=цвет (или шестнадцатеричный код цвета) определяют толщину (в пунктах) и цвет границы между областями.
Непарный тэг <frame> "открывает" информацию части экрана (по порядку: слева направо и сверху вниз): можно вводить произвольные
тексты, таблицы, картинки и т. д., таким образом, каждая часть экрана
оформляется как отдельный документ. Каждый из построенных документов может быть связан с остальными. Для построения этой связи
полезно использовать атрибут name="…" тэга <frame> и тогда необходимую засылку в нужную часть можно выполнить тэгом <A> с
атрибутом target="имя части". Если есть необходимость заполнить
фрейм некоторым готовым HTML-документом, то следует использовать тэг <frame> с атрибутами src="адрес вводимого документа" и
target="имя фрейма". Рассмотрим следующий пример.
Пример. Построим Htm – документ с использованием фреймов.
Тема документа – моя семья. Разобьем экран сначала на две равные
вертикальные части. Вторую обозначим "frC", первую разобьем на две
равные горизонтальные части, обозначив верхнюю "frA", нижнюю –
"frB". Заготовим документ "Part_С.htm", который будет загружен во
фрейм "frС", содержащий полезные общие сведения о семье. Общую
схему кода этого документа можно представить следующим образом:
<html>
<!- - необходимая часть, заполняемая редактором -->
<head> <title> Part_С </title> </head>
<body>
<h2 align=center>
<!- - красный заголовок -->
<font color=red> Как мы живем </font>
</h2>
<!- - далее произвольная информационная часть - ->
134
...
</body>
</html>
(в угловых скобках <! - - комментарий - -> не воспроизводится браузером).
Далее, заготовим файлы фотографий членов семьи, например, в
формате .jpg (или .gif, .tiff, .xbm) и на каждого члена семьи небольшой
документ для загрузки фотографии. Возьмем для примера отца и назовем документ father.htm:
<html>
… <! - - заголовки - ->
<body>
<h2 align=center> Портрет отца </h2>
<image align=bottom src="(адрес файла)....jpg">
</body>
</html> .
Пусть наша семья состоит из родителей и троих детей (два брата
и сестра). Подготовим документ, загружаемый во фрейм "frA":
<html>
<head > <title> Part_A </title> </head>
<body>
<!- - подчеркнутый заголовок - ->
<h2> <u> <center> Моя семья </center> </u> </h2>
<UL> <!- - список - ->
<Li> <b> <i> Родители </i> <b> <!- - жирный курсив - ->
<UL> <!- - подсписок - ->
<Li> <a href="father.htm" target="frB">
Отец </a>
<!- - загрузка фотографии при щелчке мышкой по слову "Отец" - ->
<Li> <a href="mother.htm" terget="frB">
Мать </a>
<!- - загрузка фотографии при щелчке мышкой по слову "Мать" - ->
</UL>
<Li> <b> <i> Дети </i> <b>
<UL>
<Li> <!- - подсписок детей - >
</UL>
</UL>
</body>
</html> .
Наконец, соберем все в едином документе "Main.htm" с кодом:
<html>
<head> <title> Main </title> </head>
<!- - разбиение экрана на две вертикальные рамки - ->
<frameset cols="50%,50%">
<!- - разбиение первой части на две горизонтальные
половины - ->
<frameset rows="50%,50%">
<frame src="Part_A.htm" name="frA">
135
<frame src="Part_B.htm" name="frB">
<!- - документы в окна загружены - ->
</frameset>
<frame src="Part_C.htm" name="frC">
</frameset>
</html>
(здесь документ Part_B.htm содержит один заголовак "Фото"; эту
строчку можно опустить). Созданный таким образом документ состоит из трех связанных частей (фреймов): в левой верхней части – список членов семейства, в правой – все, что хотелось сообщить о семье.
При щелчке мышкой по какому-нибудь элементу списка в левом нижнем фрейме появляется соответствующая фотография с подходящей
надписью.
HTML-документы позволяют использовать так называемые "плавающие" фреймы. Они остаются на той же странице просмотра, занимая место наподобие поля вставленного рисунка в Word. Плавающий
фрейм определяется парным тэгом <IFrame> с атрибутами align=
выравнивание (left, center, right), height= высота в пунктах или
процентах от общего экрана, width= ширина фрейма, src="адрес
загружаемого документа". Содержимое плавающего фрейма можно
менять в зависимости от состояния основного документа (документ в
документе). Если загружаемый документ не помещается в поле
фрейма, то последний снабжается полосой прокрутки.
Безусловно, некоторые текстовые редакторы имеют, как уже отмечалось выше, достаточно подробное меню, набор шаблонов для автоматизации создания Web-документов. Базовые знания HTML существенно упрощают и облегчают эту работу. Кроме того, HTML допускает использование Visual Basic (в слегка урезанном варианте – так
называемый VBScript, а также JavaScript), а вместе с ним уже известные элементы управления, подпрограммы и макросы. Все это позволяет превратить Web-документ в очень "живое" Internet-приложение.
136
6. Элементы вычислений в Mсd
В целом мы уже знакомы с некоторыми основными приемами работы в Mcd. Соберем теперь разрозненную информацию воедино.
6.1. КРАТКИЙ ОБЗОР
Переменные – типа Double, String, Complex.
Окончания "b", "o", "h" обозначают число в двоичном, восьмеричном или шестнадцатеричном виде (например, A2Ch обозначает
16-чное число 12+2∙16+10∙256, т.е. 2604).
307
-3
Константы: ∞ = 10 , tol = 10 (точность числ. методов),
ORIGIN = 0 (начало индексации, можно менять!), % = 0.01, i (или
j) = -1.
Операторы: 1) присваивание ":=" (на рабочем листе, клавиша
Shift "ж"), "←" (в блоках, клавиша "{"),
2) вычисление (вывод значения) "=" (на рабочем листе, "="),
"→" (в символьных вычислениях, клавиша Ctr "."),
3) обработка условия (клавиша "}")
, альтернатива
оператор
условие
вводится оператором "Otherwise" (клавиша Ctr "}"), не путать
с функцией if (■, ■, ■), возвращающей результат действия, где
на первом месте стоит условие, на втором – оператор, выполняемый при этом условии, на третьем – альтернативный оператор.
4) логическое "=" (толстое) вводится клавишей Ctr "=",
5) многоточие (знак ранжированных значений, кл. ";" ) "..",
6) верхний индекс (степень) – Shift "6",
7) нижний индекс – клавиша "[" (не путать с "подписью" – кл. ".":
например, после ввода "a[10" и "a.10" на рабочем листе в обоих
случаях появится выражение a10, но в первом случае это элемент массива, во втором – отдельная переменная),
‹■›
8) верхний индекс в угловых скобках (кл. Ctr "6") M определяет
номер столбца матрицы (в данном случае матрицы М),
9) знак транспонирования (это не степень!) вводится клавишей Ctr
+ "1",
10) цикл пересчета "for ■ ■..■" (клавиша Ctr+Shift "Э") допускает
прямой и обратный ход (отсутствует форма "Step"), а также вариант "for ■ ", где а – произвольный вектор-строка.
11) цикл с предусловием "While ■ (условие)" – других циклов нет,
137
12) блок операторов
■
■
вводится из меню "Add Line" или клавишей
"]" (правая квадратная скобка), для добавления блока в оператор
(или увеличения блока) достаточно выбрать мышкой место
(или определить законченную область) и щелкнуть "Add Line"
(или нажать "]" на клавиатуре), например, условный оператор
■ if ■ после выделения левого "места" и нажатия "]" превращаif ■
■
ется в
,
■
13) "Break" (кл. Ctr "{") выполняет "принудительный" выход из
циклов,
14) греческие буквы вводятся как соответствующие латинские
с последующим нажатием Ctr "g" (либо из меню).
Функции: 1) встроенные (калькулятор или Меню вставка f(x)),
2) пользовательские, определяются следующим образом:
 ариф. выр. 
_
имя (аргументы – не обязательно) : −  функция , переменблок прогр.
ные справа от знака присваивания должны входить в число аргументов (слева) или быть определенными ранее (т.е. левее и
(или) выше). Например, функция f(x) x+sin(ω∙x+c) не определена, если переменные ω и с не были определены ранее (вычислены или приняли значения), х – фиктивная (свободная)
переменная (ее определять не обязательно). Переменные, определенные внутри функции, не доступны вне ее.
Mсd допускает рекурсивное определение функции (через ранее
вычисленные значения).
1 при |x| < 0.0001,
Примеры. 1) Вычислим функцию f(x) =  x
с помощью
x
f( /2) cos( /2) иначе
_ if (|x| < 0.0001, 1, f(0.5∙x)∙cos(0.5∙x)).
кода f(x) : −
2) Функцию, вычисляющую n-ое число Фибоначчи fn = fn-1 + fn-2,
_ if(n < 2, 1, f(n-1) + f(n-2)).
f0 = f1 = 1, легко определить кодом f(n) : −
Индексированные объекты (векторы, матрицы, тензоры) определяются двояко:
1) меню "матрицы" (клавиша Ctr "m") позволяет ввести требуемый шаблон для заполнения,
2) при известных функциональных свойствах объекта можно
определить границы массива (например, m ..., n ...) и задать ранжированные индексные переменные, полагая в этом
случае (при ORIGIN = 0) i 0..m-1, j 0..n-1, после чего мо-
138
жно задавать значения объекта присваиванием: Obi, j
...
Например, пусть необходимо определить матрицу А, имеющую 100 строк и
столбцов, диагональные элементы которой равны 4, соседние 1, остальные нули. Положим m 100 n 100 i 0..m-1 j 0..n-1
A i, j if(i = j, 4, if(|i – j| = 1, 1, 0)). Результат можно проверить, вставив
знак "=" после имени матрицы А.
Графики (см. рис. 45).
I. 2-мерный график:
а) декартов (X-Y график),
б) полярный график.
II. 3-мерный график.
а) график поверхности,
б) график линий уровня,
в) 3-мерная гистограмма,
г) 3-мерное множество точек,
д) векторное поле.
Рис. 45
Начиная с 12-й версии, Mсd допускает плоские графики с двумя
осями ординат с независимой шкалой. На осях указываются соответствующие пары аргумент-функция (от указанного аргумента) или пары множеств {x}-{y}. На одном графике можно изобразить несколько
функциональных зависимостей.
Пример 1. Плоский график функции x(t) =
(t-1)2
t3-2t+2
, y(t) =
, заданной
t
2t
параметрически, вместе с асимптотами 0.5 (t+2)2-2 и t+1 представлен одним изображением
парами
{x(t), y(t)}, {t, 0.5(t+2)2-2} и
{t, t+1} (по оси ординат ввод
следующего графического
объекта выполняется после запятой, как и по оси абсцисс,
см. рис. 46).
Пример2. Полярный график функции
 1 
expsin(πt)-1


r(t) =
1+0.2t
(трилистник) изображен на
рис. 47.
Рис. 46
139
Форматирование графика
(щелчок правой мышью по
графику выбор "Формат")
позволяет менять тип, толщину, цвет линий графика, количество и масштаб элементов сетки, фон, и т.д.
Пример 3. Быстрое построение
графика поверхности: определяется функция двух переменных (см.
рис. 48), вставляется панель графика поверхности, в место (черный
квадратик) внизу рамки вставляется имя функции (в данном случае f).
Можно определить значения функции на прямоугольной равномерной сетке значений аргументов (с постоянным
шагом) в виде матрицы (прямоугольной
таблицы), тогда в нижней части рамки
графика следует поставить имя этой матрицы. Можно, наконец, использовать
встроенную функцию CreateMesh, которая сама формирует необходимые матрицы для изображения графика в нужном диапазоне данных (с заданной подробностью). Так, если было бы желательно посмотреть на графике поведение
данной f(x,y) в области x [-2,2], y [0,3],
можно определить комплект матриц M
CreateMesh(f,-2, 2, 0, 3, 20, 30) с 20
значениями по х и 30 значениями по у.
В результате получили бы следующий
рисунок (см. рис. 49).
Рис. 47
Рис. 48
Пример 4. Если поверхность задана параметрически, то ее следует оформить в виде вектора с тремя координатами (x, y, z). Построим график тора с большим радиусом R=10 и
маленьким r = 4, лежащего в горизонтальной
плоскости. Введем параметры: u∈ [0, 2π] –
угол поворота в плоскости тора, v∈ [0, 2π] –
угол поворота в вертикальной плоскости. То-
Рис. 49
140
гда абсцисса точки поверхности будет представлена функцией x = (R+r cos(v)) cos(u), ордината - функцией y = (R+r cos(v)) sin(u), аппликата
z = r sin(v). В функции CreateMesh возьмем по
50 точек в области изменения каждого параметра. В результате получим следующий рисунок
(см. рис. 50).
Аналогично получаются линии
уровня функции f (см. рис. 51) и 3-D
распределение точек тора (рис. 52).
Рис. 51
Рис. 52
Пример 5. Для построения графика (распределения) плоского векторного поля полезно определить две матрицы: одна – матрица абсцисс
векторов, другая – ординат. Пару этих матриц
(в скобках) следует поместить внизу рамки поля графика. Так, например, для векторного по2 2
T
 x -y

ля F(x, y) = x2+y2, y cos(x-y) в области [-2, 2]


×[-3, 2] положим: n := 10, hx := 0.4, hy := 0.5, i :=
0..n, j := 0..n, Zi,j := F(i∙hx-2, j∙hy-3), Mi,j := (Zi,j)0,
Ni,j := (Zi,j)1. Выбрав в меню (см. рис. 45) график векторного поля и указав внизу пару матриц (M, N), получим рис. 53.
Рис. 50
Рис. 53
Символьная математика:
а) символьные преобразования,
б) символьные вычисления.
Меню символьных преобразований вызывается
выбором "шапочки" в меню "Математика" (рис. 54).
Рассмотрим использование некоторых ключевых слов
из этого меню (результат получается после ввода праРис. 54
вой стрелки "→" – Ctr ".").
■ float, n позволяет вывести результат с n десятичными знаками (с
плавающей запятой), например, π float, 12 → 1.77245385091.
141
■ rectangular позволяет записать комплексное число в прямоугольln(5)
ных координатах, например, ln(1-2∙i) rectangular →
- atan(2)∙i
2
(разделение действительной и мнимой части при условии, что i = -1).
■ solve [, имя переменной] находит возможные решения уравнения,
при этом ключевым словом assume можно задать область поиска решения, например, если требуется найти действительные решения уравнения (x3-1)(x2-2) = 0, то записав это равенство, следует ввести ключевое слово solve, затем assume, после которого записать x = real, и выйти мышкой за пределы формулы:

solve
(x – 1)∙(x – 2) = 0 assume, x = real → 

3
1 
2 .
- 2
2
■ simplify позволяет упростить алгебраическое или функциональное
выражение, например,
2
2
2
2
(x+y)2-y4
x +xy-2y +10(x-y) x +3xy+2y -2(x+y)
+ x2+2xy-y2(x-1)-y3  ∙ (x-y)∙(x+4y)+4∙(x+y) simplify → 2.
 x2-y2+xy2-y3


■ substitute, ■ = ■ выполнить подстановку в функциональном выражении (замену переменной) с последующим преобразованием полученного выражения.
■ factor разлагает выражение на сомножители, например,
16936 factor → 23∙29∙73.
■ expand позволяет раскрыть скобки в алгебраическом выражении,
привести подобные члены или записать его в виде более простых функций, например,
expand
8∙sin(x)∙cos(4∙x)3 simplify → 3∙sin(5∙x) - 3∙sin(3∙x) – sin(11∙x) + sin(13∙x).
■ coeffs выписывает коэффициенты многочлена (относительно
данного выражения) в порядке возрастания, например,
2
2
2
2
3∙x ∙y+5∙x ∙y +7∙x∙y +x∙y
 02 
coeffs, x →  7∙y +y  .
5∙y2+3∙y
■ collect, ■ приводит подобные члены относительно выбранной
переменной, например,
3∙x2∙y+5∙x2∙y2+7∙x∙y2+x∙y collect, y → (5∙x2+7∙x)∙y2 + (3∙x2+x)∙y.
■ series позволяет получить разложение функционального выражения
в ряд по степеням выбранной переменной, например, найдем разложение 8∙sin(x)∙cos(4∙x)3 в ряд по степеням х до четвертой степени:
142
series
580∙x3
8∙sin(x)∙cos(4∙x)3 x, 4 → 8∙x .

3
■ parfrac помогает (в некоторых случаях, особенно, когда известны
корни знаменателя) разложить дробь на сумму простейших, например,
4∙x2-3∙x+1
4
3
- 2 .
parfrac
→
3
2
x +x +x+1
x+1 x +1
■ confrac конструирует непрерывную дробь, например,
x3+x2+x+1 confrac
4∙x2-3∙x+1 x
или 1 + 1



→



1
1
4
-16
9
-27
44
121
144
48
11


x
,
x

x

0
x
x
x
x
4 + -16
x
+
9 -27
x
44 + 121 x
44 + 48
11
Рис. 55
В символьных вычислениях могут участвовать многие встроенные функции и операторы (если задача предполагает наличие символьного результата). Чаще всего при этом имеются в виду операторы и
функции анализа (см. рис. 55). При этом последующий знак равенства
предполагает числовой результат, правая стрелка – символьный.
16∙t+1
b
Например, пусть a := 0, b := 4, f(t) := t2+t+1 , тогда ∫ f(t) dt = 17.429, но в
a
7∙π∙ 3 14∙ 3∙atan(3∙ 3)
. Это
9
3
a
касается и всех остальных функций и операторов.
b
тех же условиях ∫ f(t) dt → 8∙ln(21) +
143
Задачи оптимизации
Большая и важная часть задач, решаемых в MathCad, составляет
задачи оптимизации, т.е. задачи отыскания минимума или максимума
числовой функции. Так как max f(x) всегда можно записать как - min
(-f(x)), то можно вести речь именно о минимизации.
Mсd имеет несколько встроенных функций для этой цели: Min(...),
Max(...), находящие минимум (соотв. максимум) на заданном (в виде
чисел, векторов, матриц) конечном мнoжестве числовых значений,
функции Minimize(f, x, ...), Maximize(f, x,...), Minerr(x,...).
Безусловный минимум (максимум) легко найти из
условий Ферма: grad f = 0. Оптимизировать функцию при наличии условий целесообразно в блоке
Given
условия (равенства, неравенства) , где Given – слуMinimize(f,...) =
Рис. 56
жебное слово (вводится с клавиатуры), условия используют операторы
сравнений из логического меню (см. рис. 56), оптимизирующая функция вводится из меню "вставка функций". При численном решении задачи перед блоком необходимо задать подходящие начальные значения параметров задачи (от их выбора может зависеть результат).
Пример 6. Пусть требуется найти наименьшее
x2 y2
расстояние между точками эллипса 9 + 25 = 1 и тоx y
чками прямой 6 - 8 = 1. Определим функции f(x,y)
x2 y2
x y
:= 9 + 25 , g(x,y):= 6 - 8 , φ(x,y,u,v):= (x-u)2+(y-v)2.
Из геометрических соображений следует, что решение должно быть в четвертом квадранте, поэтому
положим x:= 0, y:= -1, u:= 2, v:= -3. Запишем блок
Given
решения: f(x,y) = 1 g(u,v) = 1
. Далее, запишем R
R Minimize(φ,x,y,u,v)
и знак равенства (вывод результата), получим
RТ = (1.874 -3.905 2.64 -4.48), (R0, R1) – координаты
точки на эллипсе, (R2,R3) – соответствующие координаты на прямой (см. рис. 57).
Рис. 57
Об использовании функции Minerr в задачах оптимизации и при
решении уравнений речь пойдет позже.
144
Алгебраические уравнения и системы
В общем случае можно использовать аналогично предыдущему
Given
блок уравнения , функция Find вводится из меню "вставка функFind(...)
ций" (функция может применяться и для символьного решения, если
такое возможно). При численном решении необходимо до блока задать
начальные значения поиска решения.
Пример 7. Найдем все решения системы уравнений
1+xy = 18xy
x+y
.

208(xy)2
2
1+(xy) = x2+y2
Введем блок с условиями
и с последующей символьной операцией
Find(x,y) simplify →, в результате которой получим:
все решения системы.
Такой результат не всегда возможен. Для численного решения
3.732
положим, например, х:=10, у:=0, тогда получим Find(x,y) = 0.072.


Полиномиальное алгебраическое уравнение вида a0 + a1x + a2x2
+...+ anxn = 0 можно решать с помощью встроенной функции
polyroots(a), в скобках – вектор коэффициентов полинома. Например,
2
-4
для уравнения 2- 4х+3х3 = 0 с коэффициентами многочлена а = 0
 
3
имеем:
- найдены все корни.
145
Векторы, матрицы, СЛАУ
Решение СЛАУ (систем линейных алгебраических уравнений)
опирается, в основном, на правила векторной и матричной алгебры.
Прежде всего, это:
сложение,
умножение на число,
скалярное умножение,
транспонирование,
векторное умножение (a×b = a∙bT),
матричное умножение,
векторизация:
sin(x0)
x0
→ 



x
sin(x
если x =  1, то sin(x)= 
1) , или, например,

x2
sin(x2)
→
 1  4  4 
 3 ∙4 = 12.
    
-2 3  -6 
Вычисление определителя |A| матрицы А,
Вычисление обратной матрицы А-1 и произвольной целой ее степени.
Имеется также много встроенных функций для работы с векторами и матрицами:
rank(A) вычисляет ранг матрицы А,
sort(P) (также rsort(∙), csort(∙)) сортирует вектор Р (матрицу по строке
или столбцу) в порядке возрастания,
identity(n) возвращает единичную n×n матрицу,
last(x) возвращает индекс последнего элемента вектора х,
cols(A), rows(A) возвращают количество столбцов или строк матрицы,
submatrix(А,iн,iк,jн,jк) возвращает подматрицу матрицы А с элементами
Ai,j, i∈ [iн,iк], j∈ [jн,jк] (н – "начало", к – "конец"),
augment(A,B) приписывает матрицу В к матрице А справа,
stack(A,B) приписывает матрицу В к матрице А снизу,
eigenvals(A) возвращает собственные значения матрицы А,
eigenvecs(A) возвращает собственные векторы матрицы А.
В зависимости от выбранной векторной нормы || ∙ || вычисляются
различные нормы матрицы: ||A|| = sup ||Ax||.
||x|| = 1
lsolve(A,b) возвращает решение СЛАУ Ax = b с квадратной невырожденной матрицей А,
+
geninv(A) возвращает обобщенную обратную матрицу A = (ATA)-1AT,
если rank(A) = cols(A) (строк не меньше, чем столбцов, ранг равен
числу столбцов). Эта матрица возникает при необходимости найти
приближенное решение переопределенной СЛАУ с матрицей полного
ранга, наилучшее в смысле наименьших квадратов (т.е. минимизиру-
146
ется величина (Ax – b)T(Ax – b) – сумма квадратов отклонений).
И много других функций.
Практически СЛАУ в MathCad решаются, в основном, двумя
способами:
а) методом обратной матрицы,
б) модификациями метода Гаусса с помощью функции lsolve.
Переопределенные системы "решаются" приближенно методом
обобщенной обратной матрицы geninv.
Пример 8. нужно найти наилучшие значения
x2x+-yy==11
(х, у), из системы равенств x - 2y = 1. Составим маx - y = 1
 12 -11 
11
трицу А =  1 -2  и правую часть b = 1. Тогда ис 1 -1 
1
0.697
комые значения суть geninv(A)∙b =  -0.03  (на рис. 58
Рис. 58
приведены графики линий, определяемых уравнениями, и точка-псевдорешение).
Неопределенные СЛАУ имеют бесконечно много решений, из которых можно, например, выбрать ближайшее к нулю. Тогда на помощь
приходит функция minimize.
Пример 9. Найдем вектор наименьшей длины, удовлетворяющий системе
x0 - x1 - x2 + x3 = 4
уравнений:  x + 2x + 3x = 6 (т.е. выберем решение, ближайшее к нулю).

1
2
3
 1 -1 -1 1 
4
Положим n:= 4, i:= 0..n-1, xi := 0, A:=  0 1 2 3 , b := 6, f(x):= x∙x (или f(x) :=
1
Given
-0.571

A∙x = b
|x|), введем блок
и получим х = -0.143  . Эту задачу можно
x := minimize(f,x)
 2.286 
решить также аналогично предыдущему примеру, используя другой вид псевдообратной матрицы (соответствующей функции в Mсd нет): x := AT(A∙AT)-1∙b с тем
же результатом. Начиная с версии Mсd13 все это реализовано в функции lsolve.
4
Пример 10. Возьмем произвольную матрицу B :=  -2
3
0
2 3
0
1
2
4
 33 -2 -12
матрицу М := B ∙B, M =  -2 30 12
 -12 12 10
T




-1
-2
1 , построим
0
2

. Матрица M положительно определена


147
 33 -2 
(т.к. 33>0,  -2 30 >0 и |M| = 1364 > 0) и из нее можно извлечь квадратный
корень, т.е. найти матрицу Х: Х2 = M. Положим сначала Х := identity(3), затем
создадим блок "given - find", записав: Given XT = X X2 = M X := Find(X). В
 5.529 0,049 -1.558
результате получим X =  0.049 5.232 1.619
 -1.558 1.619 2.225

.


Пример 11. Определим тип кривой, заданной уравнением 3х2 - 4ху + 4у2 =1, и
построим ее график. Левая часть уравнения представляет собой квадратичную
x
 3 -2 
форму (x, y)Ay с матрицей A=  -2 4 . Найдем ее
собственные векторы, полагая λ:= eigenvals(A), λ =
1.438
5.562 – таким образом, данная кривая эллипс (с
центром в нуле). Найдем собственные векторы в виде матрицы H := eigenvecs(A). Убедимся, что собст‹0› ‹1›
венные векторы ортогональны: H ∙H = 0. Запишем
параметрическое уравнение эллипса в собственном
H ∙cos(t) H0,1∙sin(t)
базисе: x(t) := 0,0
+
,
Рис. 59
λ0
λ1
H1,0∙cos(t) H1,1∙sin(t)
y(t) :=
+
и построим график вместе с собственными осями
λ0
λ1
координат (см. рис. 59, красная линия – данная кривая, синие прямые – новые оси
координат в собственном базисе).
Обыкновенные дифференциальные уравнения
(ОДУ) и системы
Задача Коши (с начальными условиями)
Для одного уравнения y(n)(x) = f(x,y,y',...,y(n-1)) c условиями x = x0, y(x0)
Given
(n-1)
= y0,..., y (x0) = yn-1 можно использовать блок уравнение и условия ,
s Odesolve(x,T)
где x∈ [0, T], уравнение записывается с использованием символов
меню анализа (или введением нужного числа штрихов с помощью Ctr
+F7 с обязательным указанием аргумента).
Пример 12. Рассмотрим нелинейный осциллятор (модель колебаний),
заданный уравнением ω2y''(t) +βy'(t) + y(t)(1+γy'(t)) = 0 при ω = 0.5, β = 0.2, γ = 1, y(0)
= 0, y'(0) = 2. Положим ω := 0.5, β := 0.2, γ := 1, Т := 20. Запишем блок
Given
ω2∙y''(t)+β∙y'(y)+y(t)∙(1+γ∙y(t)) = 0
d
и обозначим z(t) := y(t). Зависимость решения
y(0) = 0 y'(0) = 2
dt
y := Odesolve(t, T)
от t и фазовая картина (зависимость z(t) от y(t)) представлены на рис. 60.
148
Рис. 60
В старших версиях MathCad функция Odesolve может применяться и для решения системы ОДУ (в этом случае первый аргумент
функции содержит вектор имен искомых функций), а также для решения несложных краевых задач.
Пример 13. Система уравнений:
y'(t) - 2y(t)z(t) + 2 = 0

z'(t) + z(t) - 3y(t) + t =
0 с краевыми условиями
y(0) = 0, z(2) = -3 может быть решена, как показано на рис. 61.
Такие ситуации довольно редки. Чаще
всего дифференциальные уравнения и системы с начальными условиями решаются
приближенно численными методами, реализованными в функциях:
rkfixed(y0,t0,t1,N,D) - метод Рунге-Кутты с постоянным шагом интегрирования,
Rkadapt(y0,t0,t1,N,D) – то же, с переменным шагом,
Bulstoer(y0,t0,t1,N,D) – метод БурлишаШтера. Здесь у0 – вектор начальных зна-
Рис. 61
чений задачи Коши, t∈[t0, t1], N – число точек, в которых метод находит решение, D(t, y) – правая часть системы уравнений, записанной в
нормальной форме системы первого порядка, разрешенной относительно производных искомых функций.
Пример 14. Запишем уравнение нелинейного осциллятора, рассмотренное
выше, в виде нормальной системы уравнений, полагая y0(t) = y(t), y1(t) = y'(t),
0 y0' = y1
вектор начальных условий y = 2: y ' = - ω-2(βy + y (1+γy )) , т.е. в виде век 1
1
0
0
торного уравнения y(t) = D(t,y), где функция D имеет вид D(t,y) =
y1


-ω-2∙(β∙y1 + y0∙(1 + γ∙y0)). Используем rkfixed, взяв на промежутке [0, T] N = 200
точек решения. Функция R := rkfixed(y,0,T,D) возвращает матрицу с N+1
строками и n+1 столбцами, где n – порядок уравнения или системы (в данном
149
‹0›
случае n = 2). Первый столбец матрицы R содержит моменты времени резуль‹1›
тата (индексация начинается по умолчанию с нуля), второй R - значения реше‹2›
ния в эти моменты времени, третий R - значения производных в этих точках.
‹2›
‹1›
Если теперь построить плоский график R в отношении R , то получим правую
часть рис. 60.
Для жестких систем ОДУ (в которых скорость изменения искомых переменных может сильно различаться) эти методы могут давать
ложный результат (либо вообще не работать). Здесь полезно использовать функции:
radau(y0,t0,t1,N,D,k,s) – метод RADAUS,
stiffb(y0,t0,t1,N,D,J) – метод Бурлиш-Штера,
stiffr(y0,t0,t1,N,D,J) – метод Розенброка.
Здесь первые пять параметров имеют тот же смысл, что и выше, J –
матрица Якоби (условно "якобиан") правой части D системы уравнений.
Пример 15. Запишем уравнение Ван дер Поля y'' = μ(1-y2)y' - y, μ = 2000, с
начальными условиями y(0) = 0.001, y'(0) = 0, в виде нормальной системы уравнеy1


ний с правой частью D(t,y) := μ(1-y 2)y -y , "якобиан" правой части (производная
0
1 0
0
1
0

по t и у) имеет вид J(t,y) =  0 -2μy y -1 μ(1-y 2) . На промежутке [0, 2.6] найдем
0 1
0
решение с N=200 точками методами Рунге-Кутты и Розенброка. Сравнительные
графики решений приведены в листинге рис. 62.
Рис. 62
150
Краевые задачи ОДУ
Для этой цели используется отдельный набор функций, реализующих, в основном, варианты метода "пристрелки":
Sbval(y,t0,t1,D,load,score) - для поиска недостающих начальных
условий в двухточечной краевой задаче.
Bvalfit(y1,y2,t0,t1,tf,D,load1,load2,score) - для поиска недостающих
начальных условий в краевой задаче с внутренней точкой.
Здесь y (или у1, у2) – вектор начальных условий с предположением о недостающих условиях, t1, t1 – границы интервала переменной
интегрирования, D(t,y) – вектор правой части нормальной системы
уравнений, load(t0,v) – вектор вводимых начальных условий с учетом
предположений, score(t1,y) – условия, принимающие нулевые значения при выполнении краевых условий.
x' = x-(4x+y-3)y
Пример 16. Рассмотрим задачу: y' = (3y-2)x-y при t∈[0,3], x(0)=3, y(3)=1.

x0 - (4∙x0 + x1 - 3)∙x1
Запишем D(t,x):=  (3∙x - 2)∙x - x , a:= 0, b:= 3, c:= 3, d:= 1, v0:= 1 (предпола1
0
1
гаемое недостающее начальное значение)
c
load(a,v) := v , score(b,x) := x1 – d, I :=
0
sbval(v,a,b,D,load,score). В результате получим I = (4.604) – подобранное недостающее
начальное условие. Далее, для N = 350 и наc
чальных условий x := I  используем функ0
цию rkfixed, полагая R := rkfixed(x,a,b,N,D)
Рис. 63
(см. листинг на рис. 63).
Обработка данных
Для обработки данных имеется много различных встроенных
функций интерполяции, фильтрации, прогноза, и т.д., их полезно обсуждать при изучении соответствующего курса. Здесь отметим один (достаточно универсальный) метод оценки параметров подходящей аналитической модели дискретных данных – метод наименьших квадраn
тов (МНК). Суть его в следующем: набор данных {yk} k=0 возможно
соответствует некоторой функциональной зависимости f(β, t) с неизвестными параметрами β, так, что, по-видимому, выполняется соотношение yk = f(β, k) + εk, k = 0,...,n, с погрешностями εк, удовлетворяющими некоторым требованиям нормальности и независимости. Тогда параметры β желательно выбрать так, чтобы сумма квадратов этих погрешностей была минимальна (отсюда и название метода). Встроенная
функция Minerr решает в указанном смысле уравнения yk = f(β, k)
151
n
( k). Чаще рассматривают функцию φ(β) = ∑k=0(f(β, k) - yk)2 и приравнивают ее к нулю в блоке given - minerr. Рассмотрим
Пример 17. Значения некоторой величины, измеренные через равные промежутки времени, имеют вид y := (72 70 62 52 100 92 80 60 90 80 68 50 64 58
48 30)T. Данные носят колебательный характер. Выясним общую тенденцию изменения данных, подобрав параболу f(a, b, c, t) := a + b∙t + c∙t2, наиболее подходящую в смысле МНК: положим n := 15, i := 0..n, определим a := 0, b := 0, c := 0 и
введем блок
Given
a
 a 63.559


2
b
∑(f(a,b,c,i) - yi) = 0   := Minerr(a,b,c) b =  5.789  .
i
 c
 c  -0.513 
Получим коэффициенты наилучшей параболы. Вычтем ее из исходных данных,
полагая zi := (c∙i + b)∙i +a, ri := yi - zi. В результате останется чисто колебательный
процесс с переменной амплитудой. Попробуем этот процесс представить функs∙t
цией φ(A, s, ω, τ, t) =A∙e ∙sin(ω∙t + τ). Возьмем для начала A:= 10, s := -0.5, ω :=
1.5, τ := 1 и введем блок
Given
A
A
18.252





s
s
-0.043 
2
∑(φ(A,s,ω,τ,i) - ri) = 0 ω  := Minerr
ω  =  1.5  .
i
τ
 τ   2.16 
Используя полученные данные, построим
окончательную модель y(t) = a + bt + ct2 +
st
+Ae sin(ωt + τ). Вычислим значения gi :=
st
(c∙i + b)∙i + a + A∙e ∙sin(ω∙t + τ) и сравним на
графике значения yi, zi, gi (см. рис. 64).
В случае несовместной системы
уравнений Minerr возвращает значение, наиболее удовлетворяющее системе (для линейных систем действие
аналогично использованию обобщенной обратной матрицы).
Рис. 64
Работа с файлами
Текстовые файлы (файлы данных)
Функции (записываются через знак присваивания, расширение файла
"prn"):
readprn("путь к файлу") – чтение данных в матрицу из текстового
файла,
writeprn("путь к файлу") – запись данных в текстовый файл,
appendprn("путь к файлу") – дополнение текстового файла.
152
 19
Пример 18. Запишем в текущий каталог матрицу С =  6
3
3 -5 0
4 2 2
-1 4 0  командой
3 -7 1 
writeprn("data.prn"):= C, прочитаем D:= readprn("data.prn"), добавим в файл матрицы строку k := (3 7 2 1) командой appendprn("data.prn"):= k.
Графические файлы
readrgb("путь к файлу") – чтение цветного изображения,
readbmp("путь к файлу") – чтение изображения в оттенках серого.
Аналогичны функции для записи изображений. MathCad позволяет
редактировать графические файлы, выполнять фильтрацию.
Пример 19. Файл "Ecoinfo.bmp", находящийся в папке "Temp" диска F, содержит текстовую информацию в графическом виде. Часть этого файла представлена
рисунком 65 (слева). Прочитаем содержимое файла в массив А командой A :=
READBMP ("F:\Temp\Ecoinfo.bmp"). Элементы матрицы суть натуральные числа
из [0, 255] (0 соответствует черному цвету, 255 белому). Попрбуем сделать изображение более четким. Положим i:= 0 .. rows(A)-1, j:= 0 .. cols(A)-1, и Bi, j := if(Ai, j <
140, 0, 255). Ниже на рис. 65 приведено исходное изображение (слева) и исправленное (справа), соответствующее в результате такой "фильтрации" матрице В.
Рис. 65
Звуковые файлы (с расширением "wav")
readwav("путь к файлу") – чтение звукового файла в матрицу,
writewav("путь к файлу",s,b) – запись в звуковой файл (s – скорость
сэмплов, b – разрешение звука в битах),
getwavinfo("путь к файлу") – создает вектор с информацией о звуковом файле.
В поздних версиях Mcd (13 и далее) имеется встроенный "мастер
импорта данных", помогающий в работе с файлами.
153
Программная среда Mсd дает возможность пользователю работать в трех основных режимах:
1. В режиме непосредственного вычисления.
2. В режиме аналитических преобразований.
3. В режиме численного моделирования и программирования.
По поводу непосредственных вычислений сказано достаточно. Режим
аналитических преобразований по сути своей не может быть универсален, поэтому так или иначе приходится прибегать к численному моделированию. К этому побуждает и то, что многие встроенные программы и функции имеют ограниченную "связь с внешним миром". Поясним это на примерах.
3
2
Пример 20. Для функции f(x) = (x0 - 2)4 +∑k=1(xk - x k-1)2 при начальном значении xk = k, k = 0, ..., 3, попытка найти минимум (очевидно, равный нулю при х = (2,
4, 16, 256)Т) с помощью встроенной функции minimize приводит к результату х =
minimize(f,x) = (1.409 1.844 3.362 11.296)T – ничего похожего. Воспользуемся теоремой Ферма и попробуем при тех же условиях найти решение уравнения f '(x) = 0,
используя оператор градиента х и блок поска решений Given – Find. Проблема
с поиском – решение не найдено. Вычислим, наконец, производную (градиент) непосредственно, вернее, приближенно, кодом:
Df(x) : = ε ← 0.0000001, p ← f(x)
for i 0 .. last(x)
y ← x, yi ← xi + ε
di ← (f(y) - p) −: ε
d
Теперь блок Given Df(x) = 0 Find(x)T= (1.918 3.679 13.534 183.172) возвращает
результат, намного более точный. Вычисление второй производной (т.е. матрицы
Гессе в данном случае) аналитически затруднительно. Но легко воспользоваться
приведенным выше кодом, слегка изменив его:
D2f(x) : = ε ← 0.0000001, p ← Df(x)
for i 0 .. last(x)
y ← x, yi ← xi + ε
‹i›
d ← (Df(y) – p) −: ε
d
Если теперь в найденой точке экстремума вычислить A:= D2f(x) и, полагая k:=0..4,
вычислить все главные определители матрицы А, получим:
|submatrix(A,0,k,0,k)| =
29.515
3.196∙103
4.618∙106
1.863
154
т.е. все эти определители положительны, по критерию Сильвестра матрица А положительно определена, следовательно, найденная точка – точка минимума.
Здесь снова в целях компактности записи нарушается правило
для операторов в Mcd: каждый оператор должен быть записан в отдельной строке (запятые для разделения операторов недопустимы!). В
качестве знака деления (с той же целью) использован (допустимый!)
символ " −: ", верхний индекс в угловых скобках обозначает столбец
матрицы, функция last() возвращает индекс последнего элемента аргумента, функция submatrix(A,i,j,p,q) возвращает подматрицу матрицы
А с элементами Au,v, i ≤ u ≤ j, p ≤ v ≤ q, вертикальные скобки возвращают модуль числа, длину вектора или определитель матрицы.
Пример 21. Бесконечные суммы и произведения, в общем, аналитически не
вычисляются, несмотря на наличие в Mcd соответствующих операторов. В таких
ситуациях требуется программирование (см. примеры 11-13 п. 1.6 и примеры следующих разделов).
6.2. НЕКОТОРЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МОДЕЛИ
Здесь будут рассмотрены некоторые простейшие методы приближенного решения популярных задач в системе Mcd, преследуя две
цели:
1) на конкретных примерах научиться программированию;
2) заглянуть в "кухню" алгоритмов, используемых в пакете
Mcd, чтобы пользоваться ими сознательно.
6.2.1. Системы уравнений
В общем, в простейшей ситуации здесь можно воспользоваться
кнопкой "Solve", блоками Given ... Find, Given ... Minerr, а также
функциями Root, Polyroot (для многочленов), Lsolve (для линейных
систем уравнений), обратной матрицей, обобщенной обратной матрицей (Geninv), а в случае двух переменных функциями Slope, Intercept.
6.2.1.1. Системы линейных уравнений
В этом пункте будет обсуждаться задача решения системы линейных уравнений вида Ax = b, где А – прямоугольная (чаще всего квадратная) матрица, х – искомый вектор, b – вектор (или матрица) правой части. Если А – квадратная невырожденная матрица, а b – вектор,
то задача легко решается либо использованием обратной матрицы (x =
A-1b), либо применением встроенной функции lsolve(A, b), возвращающей вектор решения. В противном случае следует использовать
специальные методы, выбирающие решение специальным образом.
155
А. Обыкновенная квадратная хорошо обусловленная (определитель матрицы А не слишком мал по сравнению с ее элементами) система уравнений. Ее можно легко решить методом Крамера и методом
исключения Гаусса. Программирование метода Крамера довольно очевидно:
-1
Cramer(A, b) := d  |A|
for k  0 .. last(b)
‹k›
C  A, C  b
x k  |C| ∙ d
x
Приведем также простейший вариант метода Гаусса с выбором диагональных элементов (который используется крайне редко):
Gauss(A,b) : = A ← augment(A,b)T, n ← last(b)
for i∈0 .. n
‹i›
‹i›
A ← (Ai,i)-1∙A
for j∈0 .. n
‹j›
‹j›
‹i›
A ← A - Ai,j ∙A if i ≠ j
submatrix(A,n+1,n+1,0,n)T
(сравните с текстом кода в п. 1.7.3 с выбором максимального элемента).
Пример 1. Проверьте, что исключения Гаусса по диагонали не ра1 2 3
ботают для системы уравнений с матрицей A=  1 2 4  , det(A) = 5.
4 3 2
Б. Переопределенные системы линейных уравнений полного
ранга (ранг матрицы системы равен размерности пространства аргументов) легко решаются методом псевдообратной матрицы (вариант
метода наименьших квадратов) с помощью встроенной функции
geninv(). В старших версиях Mcd этот метод включен в функцию
lsolve, возвращающую как решение, так и псевдорешение системы линейных уравнениы (см. п. 6.1, Векторы, матрицы, СЛАУ).
Если система неполного ранга, решение (или псевдорешение)
следует выбирать , исходя из каких-то дополнительных условий. Часто
это - требование минимальной нормы решения (близость к началу координат). В этом случае в основу поиска решения кладется комбинация метода исключения Гаусса с выбором главного элемента (см. п.
1.7.3) и метода псевдообратной матрицы: сначала выбирается подсистема полного ранга, далее, если ее ранг равен рангу исходной системы,
то находится решение методом исключения, иначе если подсистема
переопределена, то находится псевдорешение (geninv), в противном
случае – решение с минимальной нормой (см. п. 6.1, СЛАУ).
156
Пример 2. Для системы уравнений Aх = b с прямоугольной мат1 5
1
2 4
3
рицей A = 3 3 и правой частью b = 2 функция lsolve(A,b) воз 
 
4 2
-2
-0.2
вращает псевдорешение  0.5  . Но с транспонированной матрицей А


1 2 3 4
3
=  5 4 3 2  и правой частью b = 1 lsolve(A,b) уже не справляется.


 
Минимальное по (евклидовой) норме решение можно получить, вычи-0.233
-1
 0.033 
слив (вручную) псевдообратную матрицу: AT∙(A∙AT) ∙b = 0.3 .


 0.567 
B. В более сложных ситуациях необходимы специальные приемы. В самом деле, как правило Крамера, так и метод Гаусса для решения системы уравнений с n неизвестными требуют порядка n3 арифметических операций. Для больших систем уравнений это довольно
пессимистичная оценка (в задачах экономики решаются системы уравнений с сотнями и тысячами неизвестных). Кроме того, не всегда требуется предельная точность результата. В таких случаях может быть
полезен метод итерационного уточнения решения.
Пример 3. Рассмотрим систему линейных уравнений Ax=b с
доминирующей главной диагональю, т. е. с матрицей А такой, что

 0 при i = j
|Ai, i | >  |A i, j|. Введем матрицу Т i, j = 
i≠j

A i, j / A
i, i
,i≠j
и вектор s i = b i /
A i,i. Тогда систему уравнений можно записать в виде x = s - Tx .
Введем в пространстве аргумнтов норму ||x|| = max |xk|. Согласованная
k
с ней норма матрицы имеет вид: ||A|| = max ∑ j |Ak,j|. Легко проверить,
k
что в данном случае ||T|| ≤ δ < 1, так что итерационный процесс уточнения решения x (n + 1) = s - Tx (n), x (0) = s, n = 0, 1, ... , будет сходиться к
точному решению исходной задачи (метод простых итераций).
Действительно, если рассмотреть соответствующую последовательность отклонений ε(k) = x(k+1) – x(k) (∀k), то она получается вследствии
итерационного поцесса: ε(n+1) = T∙ε(n) (∀n). Переходя к нормам, отсюда
имеем: ||ε(n+1)|| ≤ ||T||∙||ε(n)|| ≤ δ||ε(n)|| ≤ δn||ε(1)|| → 0 (т.е. отклонения
(n→∞)
убывают со скоростью геометрической прогрессии, итерации быстро
сходятся к точному решению). На каждой итерации требуется лишь
порядка n2 вычислений, так что процесс достаточно экономный. Итерации можно оформить в виде функции:
157
ITER(A, b, e) := n  last (b)
for i  0 . . n
r  (A i, i ) -1, x i  b i ∙ r
si  xi, yi  0
for j  0 . . n
T i, j  if (i = j, 0, A i, j ∙ r)
while |x - y| > e
y  x, x  s - Ty
x
Г. Во многих задачах матрицы линейных систем уравнений оказываются сильно разреженными (бóльшая часть элементов – нули).
Эту специфику также можно "употребить во благо". Например, в случае 3-диагональных систем уравнений (А i,j = 0 при |i - j| > 1) с
доминирующей диагональю (|Ai,i| > |Ai,j+1|+|Ai,j-1|) очень эффективен метод "прогонки", использующий лишь эти три диагонали (если условие доминирования нарушено, метод может привести к большим
вычислительным погрешностям). Будем считать, что система линейных уравнений имеет вид:
 a0,1x0 + a0,2x1 = b0 ,

 ai,0xi-1 + ai,1xi + ai,2xi+1 = bi , 1  i  n - 1,
 a x + a x = b .
n,0 n-1
n,1 n
n
a0,2
b
Положим u0 = a 0 , v0 = a . Тогда из первого уравнения имеем:
0,1
0,1
x 1 = u 0 - v 0 x 1 . Если уже найдено представление (прямой ход)
xi-1 = ui-1 - vi-1 x i
(∀i ≥ 1),
(1)
то из уравнения ai,0 (ui-1 - vi-1 xi ) + ai,1 xi + a i,2 xi+1 = b i получаем
xi = ui - vi xi+1, где теперь
ui =
bi - a i,0 ui-1
ai,2
, vi =
(i = 1, 2, ...) .
ai,1 - ai,0 vi-1
ai,1 - ai,0 vi-1
(2)
Тогда из последнего уравнения xn = un, и по формуле (1) получаем x i
для всех i = n - 1, n - 2, ... , 1, 0 (обратный ход прогонки). Очевидно,
что для хранения значений ui, vi можно использовать измененные xi ,
bi . Поэтому программа, реализующая процесс прогонки, может быть
записана достаточно компактно и просто. С вычислительной точки
зрения метод прогонки имеет много очевидных преимуществ перед
методом итераций (прямой и обратный ход решают задачу полностью;
например, программа легко справляется с системой уравнений с более
чем 10000 неизвестных). В Mcd метод можно оформить в виде следующей функции:
158
Prog(A, b) := n  Last(b)
x 0  b 0 (A 0, 1) -1, b 0  A 0, 2 (A 0, 1) -1
for i  1 .. n
p  (A i, 1 - A i, 0 b i - 1) -1
x i  (b i - A i, 0 x i - 1)  p, b i  A i, 2  p
for i  n - 1 .. 0
xi  xi - bi xi+1
x
Пример 4. Найдем приближенное решение линейной краевой
задачи x(3x2+1)y''(x) + 2y'(x) – 6xy(x) = 4-12x2 на отрезке [1, 2] с условиями у(1) = у(2) = 0. Здесь нетрудно найти точное решение f(x) = 2x 1
-0.75(x2+1) - . Разобьем отрезок [1, 2] на n равных частей с шагом h =
2x
1
и заменим производные в точках деления приближенными равенстn
y -y
i
вами: y'(xi) ≈ i+12h i-1, y''(xi) ≈ (yi+1 - 2yi + yi-1)h-2, где yi = y(xi), xi =1+ n , ∀i.
После приведения подобных членов дифференциальное уравнение
превращается в линейную трехдиагональную систему алгебраических
уравнений:
(n2xi(3xi2+1)-n) yi-1 - (2n2xi(3xi2+1)-6xi) yi + (n2xi(3xi2+1)+n) yi+1 = 4-12xi2,
i = 1, ..., n - 1, y0 = yn = 0. Несложно проверить, что диагональ матрицы
системы доминирующая, поэтому удобно применить метод прогонки.
6.2.1.2. Нелинейные уравнения и системы
А. Для одного уравнения на числовой прямой простые итерации
типа xn+1 = f(x n) (n = 0, 1, ... , x 0 – начальное приближение) приводят
при n  ∞ к решению уравнения x = f(x), если выполнено (достаточное) условие |f ′(x)|  M < 1 в некоторой окрестности точного
решения.
Уравнение f(x) = 0 всегда можно привести к указанному виду,
записав его как x = x + k f(x) (k – параметр релаксации). Тогда итерации xn+1 = xn + kf(xn) (n = 0, 1, 2, …) будут сходиться при условии
|1+ kf ′(x)|  M < 1 (условие можно выполнить, если в окрестности
решения f ′(x) ≠ 0). Можно потребовать на каждом шаге выполнения
равенства 1+ kf ′(x n) = 0, откуда k = - (f ′(xn)) -1 - это метод Ньютона:
m
xn+1 = xn - (f ′(xn))-1 f(xn). Например, a получается как решение уравнения xm - a = 0 и метод Ньютона здесь приводит к итерациям xn+1 =
(m-1)x n + ax n1 - m
, х 0 = 1 (например), которые быстро сходятся к точному
m
решению для произвольного m > 1.
159
В сложных случаях производную можно заменить секущей, полаxn-1 - xn
гая k =
= - (f ′()) -1 для некоторого : (xn - )( - xn-1) > 0,
f(xn ) - f(xn-1)
что приводит к методу (секущих, квазиньютона):
xn+1 =
f(xn)xn-1 - f(xn-1)xn
(n = 1, 2, ... ).
f(xn) - f(xn-1)
Методы легко программируются. Можно записать реализацию
методов релаксации (Relax) и секущих (QuaNew) в виде функций,
возвращающих приближенное решение, значение функции на решении и число итераций (точность обоих методов одинакова).
Relax(f, x, k) := n ← 0, t ← x + 1, ε ← 0.000001
while |t - x| > 
t ← x, n ← n + 1
x ← t + kf(t)
x
 
f(x)
 n 
QuaNew(f, x) := n ← 0, z ← x + 1, ε ← 0.000001
y ← x + 100, fx ← f(x), fy ← f(y)
while |z - x| > 
z ← (fyx - fxy)(fy - fx) -1
x ← y, y ← z, fx ← fy
fy ← f(z), n ← n + 1
 z 
f(z)
 n
Пример 1. Сравним оба метода при поиске решения уравнения
ln(x) = (1 + x2) -1, или (1 + x2)ln(x) - 1 = 0, т. е. f(x) = 0, где f(x) = (1 +
x2)ln(x) – 1, и с результатом работы блока Given ... Find. Поиск
начинается всюду с точки х = 2. Обе программы дают приближенное
решение х =1.4013215 и х =1.4013216 со значением функции в
первом случае -2.610 -7, во втором 2.1410 -12. Релаксация требует при
k = - 0.1, -0.3, -0.5 n = 27, 7 и 18 итераций. Метод секущих (QuaNew)
достигает результата за семь итераций. Встроенный блок Given ... Find
находит значение х = 1.4013212 со значением функции - 1.16910 -6.
160
Б. Для нелинейных систем уравнений F(x) = 0 (F: ℝ n  ℝ n ),
используя метод Ньютона, аналогично предыдущему получим:
x (n + 1) = x (n) - [DF(x (n))] -1 F(x (n)) , n = 0, 1, ... ,
где DF(x(n)) - матрица частных производных F в точке x (n). Здесь на
каждой итерации нужно решать линейную систему уравнений
DF(x(n)) (x(n + 1) – x(n)) = - F(x(n))
относительно вектора s = x(n + 1) – x(n) . Тогда процесс уточнения решения принимает вид (здесь D(f, х) = Df(х)):
Zero(F, D, x, ) := d ← 1
while d > 
s ← Lsolve(D(f,x), f(x))
x← x–s
d ← |s|
x


 f(x)
Например, для двух функций с двумя переменными имеем:
f1(x, y) 
F(x, y) = f2(x, y) ,
 ∂f1(x,y)
∂x
DF(x, y) =  ∂f2(x,y)
 ∂x
∂f1(x,y)
∂y 
∂f2(x,y) .
∂y 
Здесть можно использовать меню Анализа (см. рис. 55). При большой
размерности пространства проще использовать собственную программу дифференцирования (см. конец п. 6.1).
Пример 2. Рассмотрим систему трех уравнений с тремя неиз2
2
 9y - 16x = 7,
вестными  4z2 - 9y2 = 5,
с отправной точкой x = y = z = 2.
 xy + xz + yz = 1
Положим n = 3 i := 0 . . n - 1 x i := 2 , введем вектор-функцию
 9(x1) 2- 16(x0)2 - 7 
f(x) :=  4(x2) - 9(x1) - 5 
x0x1 + x0x2 + x1x2 - 1 
2
2
и выполним R := Zero(f, D, x, 10 -6) . Обратим внимание на то, что результат R является вектором, компоненты которого (их нельзя назвать "координаты") также векторы. Поэтому непосредственный вывод
{3; 1}
результата в Mсd выглядит так: R = {3; 1} (каждый элемент – мат

161
рица из трех строк и одного столбца, т. е. вектор). Получим решение
- 13
R0
-2.3610 
-0.25819889
- 13 
 0.94672926 

и значение R 1 функции f: R 0 = 
 , R 1 =  1.0810 
 1.80739223 


0
- практически точно.
В тех случаях, когда точность решения не принципиальна, либо
его вообще не существует, достаточно найти псевдорешение, как результат решения соответствующей задачи оптимизации (например, в
методе наименьших квадратов). При этом можно воспользоваться
блоком Given ‹условия› Minerr.
6.2.2. Определенный интеграл
Различные практические методы интегрирования встроены в
меню Анализа (см. рис. 55). Для знакомства с методами вычисления
определенных интегралов в конечных пределах стандартно используется приближенное представление площади плоской области между
графиком y = f(x), x  [a, b] и осью абсцисс.
На каждом промежутке [t i , t i + 1], t i = a + i 
b-a
(i = 0, ... , n) фунn
кция представляется в каком-нибудь простейшем виде (что, собственно, и определяет метод приближенного интегрирования).
В формуле прямоугольников на каждом отрезке разбиения функb-a
ция считается постоянной, и тогда для h =
имеем:
n
n-1
b
I =  a f(x) dx ≈ h  i = 0 f(a + (i + 0.5)h).
В формуле трапеций на каждом промежутке функция представляется отрезком прямой. В этом случае имеем:
b
I =  a f(x) dx ≈ h∙
n-1
(f(a)+f(b)
+

f(a + ih)).
2
i=1
Вообще же, если позволить выбирать точки 0  x 1 < x 2 < ... < x k  1, то
можно определить формулу
k
1
 0 f(x) dx ≈  i = 1 a i f(x i) ,
k
(3)
где коэффициенты {a i} i = 1 выбираются так, чтобы формула была точна для многочленов наиболее высокой степени. При k = 1, x 1 = 0.5,
a 1 = 1 имеем формулу прямоугольников, при k = 2, x 1 = 0, x 2 = 1, a 1 =
= a 2 = 0.5 получим формулу трапеций и т. д.
Наиболее популярны так называемые формулы Гаусса типа (3)
с оптимальным выбором не только коэффициентов ai , но и узлов {xi }.
Можно показать (это делается в отдельных курсах численных мето-
162
дов), что в качестве {xi} следует брать корни многочленов Гаусса,
ортогональных на [0, 1] (многочлены Pm (x) и Pn (x), m ≠ n, ортого1
нальны на [0, 1], если  0 Pm (x) Pn (x) dx = 0). Например, первые два
такие многочлена суть P1 (x) = 2х – 1, P2 (x) = 6х 2 - 6х + 1. Первый
имеет корень х = 0.5 (так что приведенная формула прямоугольников
является простейшей формулой Гаусса), второй имеет два корня x1,2 =
3± 3
и таким образом формула
6
1
 0 f(x) dx ≈ 1 [f( 3 -6 3 ) + f( 3 +6 3 )]
2
оказывается точной для многочленов 0, 1, 2, 3-й степени. Полагая s =
b-a
= 3 -6 3 , t = 1 - s, h =
, можно теперь записать
n
b
 f(x) dx ≈
a
h n-1
 [f(a + (i + s)h) + f(a + (i + t)h)] .
2 i=0
(4)
Формулы Гаусса - "открытого" типа (не используют значений функции в узлах сетки) и могут применяться к несобственным интегралам и
3
dx
интегралам типа Коши. Например, для  -1 x = ln(3) (=1.0986122…)
при а = -1, b = 3, n = 40 по формуле (4) получим значение с восемью
точными знаками. Аналогично можно построить формулы вида:
∞
 0 f(x) e -x dx ≈ 
2
k
a f(x i)
i=1 i
.
(5)
Например, при k = 3, х 1 = 0.19055415, х 2 = 0.848251867, х 3 =
= 1.799776578, а 1 = 0.44602977, а 2 = 0.396468267, а 3 = 0.043728888 и
для функции f(x) = (2 + x -2)ln(1 + x) -
1
по формуле (5) получаx(x + 1)
ем 0.99991525 при точном значении 1.
В действительности равномерное разбиение промежутка интегрирования (постоянный шаг) не всегда целесообразно и существует много способов адаптировать его к поведению функции (что Mcd и делает). Самый простой (с алгоритмической точки зрения) способ – это
использование рекурсий (см. п. 1.6). Для каждом этапе рекурсии реализуется конкретный метод интегрирования на одном шаге, шаг
(точнее, промежуток) затем делится пополам, и на каждой половине
снова вычисляется интеграл. Если результат вычисления изменился
меньше допустимой погрешности, то он выдается, как окончательный,
иначе дробится далее каждая половинка промежутка и процесс
повторяется (рекурсия). В таком случае выбор разбиения отрезка интегрирования осуществляется автоматически в соответствии с требуемой
точностью. Для метода прямоугольников, например, функция вычи-
163
b
сления интеграла ∫a f(x)dx с (абсолютной) погрешностью ε = 0.0001
выглядит так:
a+b
, h ← b-a
2
r ← h∙f(s), h ← 0.5∙h
a+s
s+b
p ← h∙f , q ← h∙f
 2 
 2 
if (|p+q-r| < ε,p+q,Int(f,a,s)+Int(f,s,b))
Int(f,a,b) := ε ← 0.0001, s ←
Пример. Для функции f(x) =
3
(= 2arctg(
1
вычислим значение интег2-cos(x)
)
3tg(1.5))
по приведенной программе и
0
3
встроенными средствами. Получили: Int(f,0,3) = 1.7665441884, Mcd
возвратил 1.7665491915, "точное" значение 1.7665491915 – требуемая
точность выполнена (с избытком).
рала ∫ f(x)dx
6.2.3. Функции на дискретном множестве
Если функция задана конечным числом своих значений, аналитическое меню Mcd оказывается бесполезным, поскольку классические операции анализа на таких функциях неопределены. Продолжение
таких функций на числовую область называется интерполяцией (восполнением) или аппроксимацией (приближением) в зависимости от
метода и цели задачи. Простейшим инструментом здесь является метод Лагранжа: если функция задана своими значениями y0, y1, ..., yn
в точках соответственно x0, x1, ..., x n, то многочлен (Лагранжа)
n
Ln (t) =  yi
i=0
(t-x0)...(t-xi-1)(t-xi+1)...(t-xn)
(xi - x0)...(xi - x i-1)(xi - xi+1)...(xi - xn)
определен для всех t и Ln (x i) = yi (i = 0, ..., n). В терминах Mcd этот
многочлен можно определить формулой
n
n
i=0
j=0
Ln(t) :=  yi  П if(i = j, 1,
t - xj
).
xi - xj
C помощью аппарата разделенных разностей этот многочлен можно
записать в ином виде.
Более гибким инструментом для решения задач интерполяции
являются сплайны, представляющие собой агрегат, гладко склеенный
из многочленов фиксированной степени (в данном случае три). Встроенные функции lspline, pspline, cspline позволяют найти значения вторых производных сплайнов по данным x ={xi}, y ={yi}, после чего сам
164
процесс интерполяции осуществляется функцией interp: сначала
вычисляется вектор vs := cspline(x, y), например, затем определяется
функция f(t) := interp(vs, x, y, t), интерполирующая массивы данных x,
y кубическим сплайном в точке t.
Пример. Пусть функция задана в точках {xi} = {0, 2, 3.5, 4.5, 7}
значениями {yi} = {0, 0, 1, 0, 1}. Интерполируем ее значения на равномерную сетку {zj = j - 1, j = 0, ..., 9} с помощью многочлена Лагранжа
(функция L(t)), сплайна с параболическими краевыми условиями (функция f(t)) и продифференцируем полученные функции. В результате
получим таблицу:
Таблица 11
z
-1
0
1
2
3
4
5
6
7
8
L(z)
7.426
0
-1.17
0
0.987
0.647
-0.78
-1.67
1
11.61
f(z)
1.288
0
-0.43
0
0.917
0.584
-0.38
-0.26
1
3.406
L′(z)
-12.2
-3.53
0.54
1.385
0.398
-1.04
-1.54
0.273
5.790 16.40
f ′(z)
-1.72
-0.86
0
0.859
0.603
-1.15
-0.46
0.687
1.833 2.979
Можно для той же цели использовать подходящую систему функций { i(t)} и подобрать в представлении R(t) =  i aii(t) коэффициенты ai наилучшим (в требуемом смысле) образом. Это линейная задача и она легко решается методами п. 6.2.1. Если в данном примере
взять r(t) = (t 2 + 1) - 1 и положить  i (t) = r(t - x i) (трансляции функции
r), a коэффициенты a i (i) выбрать из условий интерполяции: R(x i) =
yi (i), то в результате получается аналитическая кривая (см. рис. 66).
Вектор коэффициентов получается из системы линейных уравнений
Aa = y c матрицей A i, j = r(xi - xj ), i, j. Можно положить a = A- 1y (или
a = lsolve(A,y)) и определить R(t) = ar(t - x) (скалярное произведение)
либо указанной выше суммой.
Из приведенного рисунка (см. рис. 66) видно, что многочлен Лагранжа больше остальных агрегатов колеблется относительно предполагаемых значений и, конечно же, не пригоден для анализа поведения
функции (тем более, экстраполяции). Сплайны ведут себя значительно
"спокойнее" (они строятся по условию минимальности изгиба). Теоретические оценки их отклонений позволяют использовать сплайны для
приближенного дифференцирования функций. Для экстраполяции и
они не очень пригодны. Все приведенные агрегаты "безлики", а экстраполяция должна отслеживать суть явления (см., например, п. 6.2.6).
165
Рис. 66
Наконец, на равномерной сетке xi+1 - xi = h (i) можно построить
формулы приближенного дифференцирования в узлах xi вида
k
hs
=  i = 0 aiyi, где yi = y(xi), i. Используя формулу Тэйлора, из
s!
s
k
k
[(i - m)h] j
(s) h
равенств  i = 0 ai  j = 0 y(j)
=
y
+ o(hk+1) нетрудно получить
m
m
j!
s!
y (s)
m
для коэффициентов {a i} линейную систему уравнений
k


1, i = s
aj (j - m) i =  0, i ≠ s (i = 0, ..., k)

j=0

1, i = s
с матрицей A i,j = (j - m)i и правой частью bi =  0, i ≠ s . Отсюда, напри
мер, следуют популярные формулы вычисления второй производной:
y0′′h 2 ≈ 2y0 - 5y1 + 4y2 - y3, yi′′h 2 ≈ yi-1 -2yi + yi+1, yn′′h 2 ≈ 2yn - 5y n-1 +
4yn-2 - yn-3, и др. Приведем таблицу некоторых часто используемых
формул приближенного дифференцирования (табл. 12 – 13).
Таблица 12
Формулы для вычисления ym' h∙k! порядка k
m
k=2
k=3
k=4
0 -3y0 +4y1 –y2
-11y0 +18y1 -9y2 +2y3 2(-25y0+48y1-36y2+16y3-3y4)
1
-y0 +y2
-2y0 -3y1 +6y2 -y3
2(-3y0-10y1+18y2-6y3+y4)
2( y0-8y1 +8y3-y4)
2 y0 –4y1 +3y2
y0 -6y1 +3y2 +2y3
3
-2y0 +9y1 -18y2 +11y3
2(-y0+6y1-18y2+10y3+3y4)
4
2(3y0-16y1+36y2-48y3+25y4)
166
Таблица 13
m
0
1
2
3
4
Формулы для вычисления y''m h2 порядка k
k=2
k=3
k=4
y0-2y1+y2 2y0-5y1+4y2-y3
(35y0-104y1+114y2-56y3+11y4) / 12
y0-2y1+y2
y0-2y1+y2
(11y0-20y1+6y2+4y3-y4) / 12
y0-2y1+y2
y1-2y2+y3
(- y0+16y1-30y2+16y3-y4) / 12
-y0+4y1-5y2+2y3
(-y0+4y1+6y2-20y3+11y4) / 12
(11y0-56y1+114y2-104y3+35y4) / 12
6.2.4. Обыкновенные дифференциальные уравнения
Как известно, всякую задачу Коши для системы обыкновенных
дифференциальных уравнений в нормальном виде можно представить
системой уравнений первого порядка, поэтому ограничимся рассмот
рением задачи  x′(t) = f(t, x). Точное (аналитическое) решение удается

x(0) = x0
найти лишь в исключительных случаях, поэтому широко распространены приближенные (численные) методы. Простейший - способ Эйлера, использующий правую часть уравнения для проведения касательной к решению: если ti = ih (i = 0, 1, ...), то
xi = x(ti) ≈ xi-1 + hf(t i - 1, x i - 1),
что легко реализуется кодом (n задано, h выбрано):
i := 0 . . n t i := ih x i := if(i = 0, x0 , xi-1 + hf(ti-1, xi-1) .
Этот алгоритм плохо сходится даже для "хороших" задач, однако он
легко улучшается, если перемещаться по направлению среднему из направлений в соседних узлах (модифицированный метод), полагая
ki = xi + hf(ti, xi), xi+1 = xi + 0.5h(f(ti, xi) + f(ti+1 , ki)), i = 0, 1, ... .
Рунге и Кутта довели модификацию до логического конца. Приведем
пример метода Рунге - Кутты четвертого порядка (наиболее популярный в вычислительных моделях):
x i := p ← x0 if i = 0
otherwise
k1 ← f(t i - 1, x i - 1)h
k2 ← f(t i - 1+ 0.5h, x i - 1 + 0.5k1)h
k3 ← f(t i - 1 + 0.5h, x i - 1 + 0.5k2)h
k4 ← f(t i - 1 + h, x i - 1 + k3)h
p ← x i - 1 + (k1 + 2 k2 + 2 k3 + k4)6 - 1
p
167
Mсd имеет несколько встроенных функций для решения задачи Коши
различными методами (Bulstoer, Rkadapt, rkfixed, Stiffb и др.), а
также блок Given ... Odesolve для определения функции-решения
(см. п. 6.1). В "штатных" ситуациях нет необходимости вникать в суть
алгоритмов.
3
Пример 1. Найдем решение уравнения y′ = y + x2+ 1 на [0, 5] с
3y
начальным условием у(0) = 1 методом rkfixed с шагом h = 0.25 ( в 20
точках) и блоком Given ... Odesolve и сравним результат с точным ре3
шением y(x) = 3e x - x - 2 (Ctrl + F7 вводит знак производной):
3
F(t, x) := x + t +2 1
3x
D(t, y) := F(t, y 0)
r(t) :=
3
‹0›
y0 = 1 M := rkfixed(y, 0, 5, 20, D) s := M
Given
3
y′(x) = y(x) + x +2 1 y(0) = 1
3  y(x)
‹1›
f := odesolve(x,5)
| r(s) - M | = 4.311  10 - 6
3  et- t - 2
(клавиша "Ctrl+F7")
→
| r(s) - f(s) | = 2.769  10 - 5
Здесь M ‹0› = {ti} - вектор значений аргументов (сетка), M ‹1› = {yi} вектор значений решающей функции, значение функции на векторе
есть вектор соответствующих значений функции, однако результат работы Odesolve требует в этом случае векторизации (знак "→ ").
Блок Given ... Odesolve (начиная с версии 12) позволяет решать
также и системы обыкновенных дифференциальных уравнений. При
использовании различных вычислительных схем решения задачи Коши уравнение (или систему уравнений) полезно привести к системе
уравнений первого порядка, разрешенной относительно производных
искомых функций. К этой (нормальной) системе уравнний уже можно
применить подходящий алгоритм из существующего в библиотеке набора. Тем не менее, условия работы встроенных алгоритмов довольно
ограничены, и нередко приходится выписывать программы "вручную".
Пример 2. Рассмотрим задачу стрельбы в реальной среде (с сопротивлением) по мишени. Будем считать мишень пораженной, если
снаряд разорвался не более, чем в r м. от мишени. Обозначим через v =
x'(t)
v(t) = y'(t) вектор скорости снаряда. На него действует сила земного
тяготения и сопротивление воздуха. При большой скорости движения
силу сопротивления среды можно считать пропорциональной квадрату
скорости. Поэтому движение снаряда сожно описать (векторным) ура0
внением v'(t) = g – λ|v(t)|v(t) с начальными условиями: х(0) = у(0) = 0,
x'(0) = c∙cos(φ), y'(0) = c∙sin(φ), где с – начальная скорость снаряда, φ –
168
угол прицела (по отношению к горизонтали). Запишем уравнение в ви4
де нормальной системы: введем вектор u∈ℝ , полагая u0 = x, u1 = y, u2 =
x', u3 = y'. Очевидно, система уравнений теперь примет вид: u0' = u2, u1'=
u3, u2'= -λu2 u22 + u32, u3' = -λu3 u22 + u32 - g, или u'(t) = D(t,u) с правой
частью
u2


u3

D(t,u) = -λu u 2 + u 2  и
 2 22 23 
-λu3 u2 + u3 -g
начальными условиями
 00 
u = c∙cos(φ).
 c∙sin(φ) 
Здесь невозможно воспользоваться ни одной встроенной функцией,
требующей точного указания времени полета (а его-то и нужно найти!). Поэтому напишем собственный код (в нем z – координаты точки
цели в плоскости полета, r – радиус зоны поражения, h – шаг интегрирования):
Blast(u,z,r,h,D) : = t ← 0
while t ≥ 0
k1 ← D(t,u)∙h
k2 ← D(t+0.5∙h, u+0.5∙k1)∙h
k3 ← D(t+0.5∙h, u+0.5∙k2)∙h
k4 ← D(t+h, u+k3)∙h
x← x+(k1+2∙(k2+k3)+k4)∙6-1
u0
t ← t+h, p ← u 
1
if |p-z| < r
return "цель поражена", break
if u1 < 0
return "промах", break .
Решение краевых задач существенно сложнее и часто сводится к
решению подходящих задач Коши (см. встроенные функции Mcd:
bvalfit, sbval и др.). Блок Given ... Odesolve справляется и с некоторыми краевыми задачами. Многие задачи (особенно линейные) можно
приближенно решить уже известными средствами: на равномерной
сетке {x i} c шагом h производные удобно заменять разностными соотношениями (см. п. 6.2.3) и тогда задача сводится к системе (вообще
говоря нелинейных) алгебраических уравнений, которые можно решать методом Ньютона или (для линейных) прогонки (см. п. 6.2.1.1).
Пример 3. Рассмотрим такую задачу: найти функцию x(t), график которой проходит через точки (0, 2) и (2, 0) и значение выражения
(t2 + 1)x'(t) + tx(t)2 постоянно на [0, 2], т.е следует найти константу С и
функцию x(t),для которых (t2 + 1)x'(t) + tx(t)2 = C, x(0) = 2, x(2) = 0. Это
– "нестандартная" краевая задача, она встроенными средствами не
решается, но можно воспользоваться идеями существующих алгоритмов. Например, функция bvalfit подбирает начальные условия для
задачи Коши так, чтобы решение удовлетворяло краевым условиям
169
(метод "стрльбы"). При заданном С наше уравнение определяет в точке t = 0 производную x'(0) = C (угол стрельбы). Решая для разных С задачу с помощью, например, odesolve, несложно подобрать значение
константы С так, чтобы х(2) ≈ 0. Здесь много "ручной" работы – подбора. Если запрограммировать метод Рунге-Кутты, то подбор можно
z - t∙x
сделать автоматическим. Введем функцию D(t,x,z) = t2 +1 , определяющую x'(t) при С = z. Найдем решение уравнения в точке t = 2 методом
Рунге-Кутты с постоянным шагом в виде функции:
2
f(z) : = n← 200, h← , t← 0, x← 2
n
for i ∈1 .. n
k1← D((i-1)∙h,x,z)∙h
k2← D((i-0.5)∙h,x+0.5∙k1,z)∙h
k3← D((i-0.5)∙h,x+0.5∙k2,z)∙h
k4← D(i∙h,x+k3,z)∙h
x← x+[k1+2∙(k2+k3)+k4] -: 6
x
Далее, положив, например, z = 0, в блоке Given f(z) = 0 C
найдем С = -1.4.
Find(z)
6.2.5. Минимизация функций
В пакете Mathcad есть функции Minimize, Maximize, Minerr.
Если необходимо решать задачу с ограничениями (типа равенств или
неравенств), то последние записываются в блоке Given ... . Функция
Minerr минимизирует среднеквадратичную разницу левой и правой
части уравнения по выбранным
параметрам (специальная минимизация, см. п. 6.1). Указанные
функции реализуют различные
(достаточно эффективные) методы. Правый щелчок мыши по выделенной функции открывает
меню доступных методов и позволяет настроить процесс решеРис. 67
ния задачи (см. рис. 67).
"Кухня" процессов минимизации непроста, познакомимся лишь с
некоторыми простейшими (с точки зрения программирования) ее
аспектами (детали излагаются в соответствующих курсах численных
методов).
6.2.5.1. Функции одной переменной
Если производная функции неизвестна (или не интересует), то
стартуя из заданной точки с выбранным шагом, можно всегда двигать-
170
ся в сторону убывания функции (для задач на минимум), считая такое
движение "удачным". Для ускорения поиска можно увеличивать шаг
при удачном движении и уменьшать шаг, меняя его направление, при
неудачном движении до тех пор, пока шаг не станет достаточно малым. Опыт и здравый смысл показывает, что увеличивать шаг следует
осторожно, например, заменяя h на 1.2h, уменьшать же шаг следует
решительнее, например, заменяя h на - 0.2h. Приведем пример соответствующей программы-функции:
Min1(f, x, h, ) := fx ← f(x), n ← 0
while | h | > 0.2  
a ← x, x ← x + h, n ← n + 1
fa ← fx, fx ← f(x)
h ← if (fx < fa, 1.2  h, - 0.2  h)
x
 
f(x)
 n 
Пример 1. Для функции f(x) =
x4+ 1
x 2 + 1, начиная с точки х = 5 с
шагом h = 1 и  = 10 – 5, получим х = - 0.99999, f′(x) = 7.0097  10 - 6
за 70 вычислений функции (встроенная функция minimize возвращает
точное значение х = 1).
Если известны значения производной функции f′(x) = g(x), то
задача сводится к решению уравнения g(x) = 0 и можно использовать
любой оговоренный выше метод. Можно, однако, найти "удачную"
пару точек х1, х2: f′(x1)f '(x2) < 0, построить в них касательные к графику y = f(x): Y = f(x1) + g(x1)(X - x1) и Y = f(x2) + g(x2)(X - x2) и
точку их пересечения x* =
x2g(x2) - x1g(x1) + f(x1) - f(x2)
можно ввести в
g(x2) - g(x1)
число "удачных", если x*[x1, x2]. Процесс заканчивается, когда изменение g(x) на удачной паре точек станет меньше оговоренного уровня. Приведем пример программ, реализующих поиск минимума f(x)
через решение уравнения g(x) = 0 (Min2) и использующих пересечение касательных (Min3).
Min2(g, x, h, ) := n ← 1, gx ← g(x), h ← - |h|  sign(gx)
while |h| > 0.1  
a ← x, ga ← gx, x ← x + h
gx ← g(x), n ← n + 1
h ← if(gx  ga > 0, 1.2  h, - 0.2  h)
x


g(x)
 n 
171
Min3(f, g, x, h, ) := n ← 1, x2 ← x, g2 ← g(x)
g1 ← g2, h ← - |h|  sign(g2)
while g1  g2 > 0
x1 ← x2, g1 ← g2, h ← 1.2  h
x2 ← x2 + h, g2 ← g(x2), n ← n + 1
y1 ← f(x1), y2 ← f(x2), n ← n + 2
while |g1 - g2| > 0.1  
x ← g2  x2 - g1  x1 + y1 - y2
g2 - g1
x ← 0.5  (x1 + x2) if (x2 - x)  (x - x1)  0
gx ← g(x), n ← n + 2
if g1  g2 > 0
x1 ← x, g1 ← gx, y1 ← f(x)
otherwise
x2 ← x, g2 ← gx, y2 ← f(x)
x


g(x)
 n 
В условиях предыдущего примера получаем:
x4+ 1
x2+ 1
g(x) := d f(x)
dx
1


- 6

Min2(g, x, h, ) = - 2.296  10 


32
f(x) :=
x := 5
h := 1
 := 10 - 5
- 1
Min3(f, g, x, h, ) =  0  .
 46
Заметим, что если в двух соседних точках известны значения функции
и ее производных, то по этой информации можно построить кубический многочлен, минимальное (или максимальное) значение которого
найти совсем просто. Это значение можно взять в качестве отправной
точки для последующих действий (постройте соответствующий алгоритм в качестве упражнения).
6.2.5.2. Функции многих переменных
6.2.5.2.1 Задачи без ограничений. Без использования производных
самыми простыми, по-видимому, являются два метода (и их модификации):
а) покоординатный спуск к точке минимума;
б) случайный поиск.
Спуск по координатам встречается в двух главных модификациях: перебор всех координат с попыткой подвинуться по каждой к точке минимума на некоторый фиксированный шаг, шаг уменьшается, если попытки неудачны по всем координатам, иначе шаг можно увеличить (процесс продолжается, пока длина шага не станет меньше заданного уровня); вторая модификация требует одномерной минимизации
вдоль каждой координаты поочередно. Практика показывает, что с то-
172
чки зрения вычислительных затрат обе эти модификации мало различимы. Обе модификации строят в пространстве последовательность
точек, весьма медленно сходящуюся к точке экстремума, но для гладких унимодальных (т. е. с одним экстремумом) функций приводят к
вполне удовлетворительному результату
Случайный поиск организуется следующим образом: в окрестности исходной точки (старта) выбираются случайные точки, равномерно распределенные в некотором параллелепипеде (часто их количество ограничивают некоторым числом), среди них выбирается точка с
минимальным значением функции и эта точка теперь берется в качестве стартовой. Диаметр параллелепипеда может уменьшаться, если новая точка оказывается ближе к центру параллелепипеда, чем к его границе. Процесс заканчивается, когда диаметр параллелепипеда станет
меньше заданного значения.
С использованием производных можно применить теорему
Ферма, решая систему уравнений DF(x) = 0, или реализовать метод
наискорейшего спуска, метод сопряженных направлений и их различные модификации. Познакомимся кратко с первым. Так как производ∂f
∂f
∂f
ная функции f: ℝn → ℝ определяет вектор Df = ∂x , ∂x , ... , ∂x  как
0
1
n
направление наибольшего возрастания функции, то естественно двигаться к точке минимума в противоположном направлении. Ради экономии вычислений движение в выбранном направлении осуществляется
до тех пор, пока функция не перестанет убывать. Тогда находится новое направление и процесс повторяется пока перемещение больше заданного уровня чувствительности. Если D(x) - вектор частных производных функции f, то процедуру поиска минимума можно оформить в
виде кода:
Min4(D, x, e) := d ← 1, k ← 0
while (d > e)  (k < 500)
y ← x, k ← k + 1
h ← D(x), t ← 0
t ← root(D(x - t  h)  h, t)
x ← x - t  h, d ← |y - x|
x
Производную можно вычислить непосредственно, с помощью оператора градиента (меню анализа), случайным поиском, либо с помощью программы-функции (пример 20 п. 6.1).
6.2.5.2.2. Задачи с ограничениями. При наличии ограничений популярен метод штрафов, в котором к целевой функции добавляется
слагаемое, равное нулю при выполнении ограничений или принимающее большое значение (в задаче минимизации), когда хоть одно ограничение не выполняется (это – штраф). Например, при ограничении
173
P(x) = 0 эта добавка имеет вид λP(x)2, а при ограничениях Q(x) ≤ 0
2
добавляется "срезка" λQ(x) + = λ∙max(0, Q(x))2. Выбирается некоторая
возрастающая последовательность значений λ (например, λi = 10λi-1,
∀i) и при каждом λ решается задача минимизации без ограничений с
предыдущим результатом в качестве начального значения.
x3 - x2 → min
Пример 2. Найдем решение задачи |x| = 3
в блоке Given
x2+x3 ≤ 0
– Minimize и методом штрафов. Обозначим f(x) = x3 - x2, φ1(x) =
x12 + x22 + x32 - 3, φ2(x) = x2 + x3 и возьмем начальную точку х = (1, 1,
1)Т. В блоке Given – Minimise получим решение:
Given φ1(х) = 0 φ2(х) ≤ 0
z : = Minimize(f,x) zT = (3.984×10-4 2.081 -2.161) f(z) = -4.253.
Возьмем теперь λ=1, у = х (начальное значение) и выполним несколько однотипных вычислений с функцией штрафа F(x):
x: =y
λ: =10∙λ F(x) : = f(x) + λ∙(φ1(x)2 + if(φ2(x) ≤ 0,0,φ1(x)2)
y: = Minimize(F,x)
x: =y
λ: =10∙λ F(x) : = f(x) + λ∙(φ1(x)2 + if(φ2(x) ≤ 0,0,φ1(x)2)
y: = Minimize(F,x)
x: =y
λ = 10 yT = (0.019 2.162 -2.181)
λ = 100
yT = (4.709×10-3 2.122 -2.131)
λ: =10∙λ F(x) : = f(x) + λ∙(φ1(x)2 + if(φ2(x) ≤ 0,0,φ1(x)2)
y: = Minimize(F,x)
f(y) = -4.243.
λ = 1000 yT = (4.709×10-3 2.122 -2.121)
Получился несколько худший результат, но быстрее, поскольку задачи
без ограничений решаются проще. Здесь прослеживается правило: выгоднее, если возможно, задачу разбить на последовательность более
простых и легче решаемых задач.
6.2.6. Pазностная модель и прогноз
Mcd имеет много функций для обработки опытных данных
(около 20 функций в разделе Curve Fitting and Smoothing – приближение и сглаживание, семь функций в разделе Interpolation and
Prediction – интерполяция и прогноз, около 60 функций в разделе
Signal Processing – обработка сигналов, и др. – полный обзор см. в
справочной литературе). Здесь будет кратко рассмотрен вопрос об
использовании модели авторегресси (порядка р > 0) временнóго ряда
p
zi (i = 0, 1, 2, ...) вида zk+1=  izk+1-i +  (зависимость наблюдаемых
i=1
значений от предыдущих), где коэффициенты i,  (при некоторых
ограничениях на zi) находятся из условий
174
n-1
p
k=p
i=1
 (z k + 1 -   i z k + 1 - i - ) 2 → min .
Пусть фиксированы n, p, положим i := 0 .. n - 1, j := 0 . . n - p - 1,

k := 0 .. p, сформируем матрицы A j,k :=  z j + p - k - 1 if k < p, bj := zj + p.

1 otherwise
Тогда вектор искомых коэффициентов находится функцией Geninv
(обобщенная обратная матрица): s = Geninv(A)b (или minerr).
Для того, чтобы построить непрерывную модель, решим разносp-1
тные соотношения z k + 1 =  s i z k - i + s p (k  p - 1) в терминах покаi=0
зательных функций - степеней корней характеристического уравнения
p-1
r =  s i r p - i - 1. Если {r i} - корни характеристического уравнения, то
p
i=0
p-1
коэффициенты c i (i = 0, ..., p) представления z k ≈  ci r ik + c p мож*
i=0
n-1
но получить из условия  (z i - z i*) 2 → min (подробнее – см. пример).
i=0
Пример. Рассмотрим кубическую параболу
у(х) = 10х(х - 1)(х - 2),
заданную в 20 точках промежутка [0, 2] своими значениями, возмущенными равномерным "шумом", построим дискретную модель 3- го
порядка, построим прогноз последних пяти значений по предыдущим
точкам и, наконец, создадим непрерывную модель процесса.
p := 3 (порядок модели) h := 2 i := 0 . . n x i := i  h
n
y i := 10  x i  (x i - 1)  (x i - 2) m := 5 (число точек прогноза)
z i := y i + rnd(2) - 1
(равномерная помеха процессу)
n := 20
Подготовка к вычислению коэффициентов дискретной модели:
j := 0 . . n - p - 1 k := 0 . . p A j,k := if (k < p, z j + p - k - 1 , 1) b j := z j + p
s := geninv(A)  b s T = (1.121034 0.268413 - 0.562349 - 1.404969  10 - 3)
(коэффициенты разностной модели)
p-1
zp := z
v := n - m . . n - 1 zp v :=  s t  zp v - t - 1 + s p (прогноз)
t=0
Построение непрерывной модели:
a k := if (k = p, 1, - s p - k - 1) (коэффициенты характеристического многочлена)
a T = (0.562349 - 0.268413 - 1.121034 1)
r := polyroot(a)
r T = (- 0.645313 0.883174 - 0.302389i 0.883174 + 0.302389i) (корни многочлена)
d := | r 2 | d = 0.933507  := angle(Re(r 1), | Im(r 1) |)
(модуль и аргумент комплексного корня)
175
c := geninv(B)  z
B i, k := (r 0) i if k = 0
i
(d  cos(i  )) if k = 1
(d i  sin(i  )) if k = 2
1 otherwise
c T = (0.321843 -1.462531 7.331131 -0.841310)
(коэффициенты непрерывной модели)
t
t


t


h
h
f(t) := c 0  (| r 0 |)  cos
+ d  (c 1  cos   t + c 2  sin   t ) + c 3
 h 
 h 
 h 
(непрерывная модель)
Результаты можно сравнить на графике (рис. 68):
5
5
3
zi
1
zp i
yi
1
f ( t)
3
5
5
0
0.4
0.8
1.2
1.6
xi  xi  xi  t
0
2
2
Рис. 67
В пакете Mcad имеется специальная функция predict, позволяющая построить недлинный прогноз по последним значениям временного ряда. Сравним последние значения ряда z, прогнозируемые с помощью разностной модели zp, соответствующие значения "чистого"
ряда y и значения, полученные функцией predict(z, n-5, 5) (табл. 14):
Таблица 14
y
- 3.75
- 3.84
- 2.88
- 1.71
z
- 4.5328 - 3.1776 - 4.2602 - 3.7213
- 1.4280
zp
- 4.1445 - 3.9104 - 3.3896 - 2.5203
- 1.5375
predict - 1.2452 0.6200
- 3.57
2.7957
2.0844
3.0793
Можно заметить, что встроенная функция возвращает не лучший
результат.
Приведенные вычислительные примеры отнюдь не отменяют
встроенного аппарата, но показывают, что внимательное и осмысленное его использование совершенно необходимо.
176
Задания
Контрольные вопросы
1. Информация, свойства.
2. Данные, сбор, формализация, фильтрация, хранение,
кодирование, защита.
3. Кодирование числовых, текстовых, графических данных.
4. Структура данных.
5. Состав вычислительной системы.
6. Системы счисления, переход от одних систем к другим.
7. Автоматическая обработка данных: блок-схема, алгоритм,
программа.
8. Структура языка. Операторы ввода, вывода.
9. Типы данных. Определение, преобразование типов,
пользовательские типы.
10.Обработка строк.
11.Операторы разветвления и альтернативного выбора.
12.Операторы циклов.
13.Массивы данных. Обработка и преобразование массивов.
14.Функции и подпрограммы, внутренние подпрограммы.
15.Файлы данных. Типы файлов. Организация файлов данных.
16.Программирование работы с графическими объектами.
17.Создание интерфейса. Формы, элементы управления.
18.Массивы и циклы в VBA.
19.Модули, функции, подпрограммы, макросы.
20.Настройка, редактирование текста в Word. Вставка объектов.
21.Использование макросов и элементов управления в Word.
22.Обработка таблиц в Word, формулы, макросы.
23.Автоматическое создание макросов. Программирование
графических объектов.
24.Вставка "нестандартных" элементов текста. Математические
формулы.
25.Нестандартное форматирование элементов текста. Создание
логотипов.
26.Ссылки, закладки, их использование.
27.Excel. Настройка. Надстройки. Формирование меню.
28.Работа с ячейками листа в Excel, вставка, удаление, изменение
размеров и свойств.
29.Вставка графических объектов и диаграмм.
30.Модули, макросы, элементы управления в Excel.
31.Использование форм и макросов для обработки таблиц в Excel.
177
32.Связанные таблицы. Базы данных.
33.Математические вычисления в Excel, решение задач.
34.СУБД на основе Access. Способы создания таблиц.
35.Задачи, решаемые в MS Access.
36.Способы создания объектов БД.
37.MathCad: структура, настройка, интерфейс, меню.
38.Отличительные особенности языка MathCad от VB.
39.Определение индексированных объектов. Операции над
векторами и матрицами.
40.Функции пользователя, создание и использование, рекурсии.
41.Обработка условий в MathCad.
42.Реализация циклических вычислений в MathCad.
43.Вычисление бесконечных сумм и произведений.
44.Встроенные функции символьных вычислений, их
использование.
45.Вычисление пределов, определенных интегралов.
46.Типы графиков. Использование.
47.Операции и функции решения нелинейных уравнений и систем.
48.Решение СЛАУ. Обобщенное решение.
49.Неопределенные СЛАУ. Выбор решения.
50.Итерационное уточнение решения СЛАУ.
51.Решение задачи Коши для ОДУ в MathCad.
52.Решение нормальных СОДУ с начальными условиями.
Приведение ОДУ n-го порядка к нормальной СОДУ.
53.Жесткие СОДУ, решение в MathCad.
54.Решение двухточечных краевых задач для ОДУ.
55.Метод наименьших квадратов, функция Minerr.
Контрольные задачи
1. Составить блок-схему решения квадратного уравнения (входные
данные – коэффициенты уравнения).
2. Составить блок-схему решения кубического уравнения с целыми
коэффициентами, если известно, что один из корней – целое число.
3. Для произвольного введенного числа х вывести на экран монитора
3
1
sin x +
2 + |lg| x||
значение выражения
, имея при этом в виду,
- x2 1+ 1
e
(cos x + arctg x)
что для логарифма, показателя и арктангенса х – произвольное
десятичное число, а для синуса и косинуса это градусная мера угла.
4. Ввести произвольное натуральное четырехзначное число, получить
178
три числа, образуемые из введенного циклической перестановкой
цифр, сложить все четыре числа и поделить результат на сумму
цифр введенного числа. Объяснить результат.
5. Для заданного натурального n найти наименьшее основание p системы счисления, в которой запись числа симметрична.
6. Проверить, что разность любого натурального числа и суммы его
цифр делится на 9.
7. Составить программу с полным анализом корней квадратного уравнения в зависимости от его коэффициентов.
8. Вводится произвольный текст, содержащий целые числа (со знаками), разделенные произвольными символами. Найти сумму этих
чисел.
9. Пусть ta – строка двоичного представления натурального числа а.
Для чисел а и b определим строку ta#b = ta & tb. Найти a#b.
10. Произвольную строку нулей и единиц представить как последовательность ASCII-кодов. Вывести соответствующий текст на экран.
11. Вводится натуральное число n. Вырабатывается последовательность n случайных чисел, равномерно распределенных на произвольном промежутке. Назовем "горкой" число в этой последовательности, которое больше своих непосредственных соседей слева
и справа. Составить программу, не использующую массивы, выводящую на экран монитора все члены последовательности чисел,
выделяя цветом "горки". Посчитать количество "горок". Как изменится программа, если учитывать не по одному соседу слева и
справа, а по два или по три?
12. Вводится натуральное число n. Заполнить квадратный n×n – массив числами натурального ряда "змейкой": в строках с нечетными номерами естественный порядок следования слева направо, в
строках с четными номерами порядок обратный. Например, 4×4
1 2 3 4
8 7 6 5
массив должен быть заполнен следующим образом: 9 10 11 12 .
16 15 14 13
13. Организовать вывод грамматически согласованной фразы о сроке
в n месяцев для произвольного натурального n (например, 2 месяца, 15 месяцев, и т.д.).
14. Целые числа х, у занимают в памяти 2n байт каждое и записаны в
массивах x(n), y(n) As Long. Составить программу сложения и вычитания этих чисел. Организовать вывод результата на экран.
15. Вводится произвольный текст. Вывести все слова текста (без
знаков препинания) в алфавитном порядке (первая буква каждого слова прописная).
16. Составить блок-схему решения следующей задачи: в заданной ма-
179
трице А найти все пары похожих строк (два множества назовем похожими, если они различаются лишь расположением элементов).
17. По заданному натуральному n создать массив натуральных чисел
(1, 2, ..., n). Каждое обращение к программе выбрасывает из массива к-е по (круговому) счету число и выдает его на экран. При выдаче последнего – сообщение: "Конец работы".
18. Массив элементов (текст, случайное число) упорядочить по убыванию чисел.
19. Построить программу, вычисляющую "диаметр" массива, равный
разности между максимальным и минимальным значением элементов.
20. Для произвольной прямоугольной таблицы чисел решить, имеет
ли она седловую точку: max min Ai,j = min max Ai,j = r. Если имеет,
i
j
j
i
выдать значения r, i, j, иначе - сообщение: "Седловой точки нет".
21. Прямоугольный массив неотрицательных чисел содержит произвольные (случайные) веса частиц. Самая тяжелая частица распадается, распределяя свою массу между остальными. Найти положение в массиве последней частицы.
22. Одномерные массивы А и В одинаково упорядочены. Объединить
массивы, сохраняя порядок.
23. Пара действительных чисел (х, у) представляет собой комплексное
число. Написать программу умножения и деления двух комплекcных чисел.
24. Для матрицы А = (Ai,j) найти норму ||A|| = max ∑ j |Ai,j|.
i
25. Массив М = {mk: k = 0, ..., n} упорядочен по возрастанию. Для произвольного х найти номер k позиции в массиве такой, что
mk ≤ x ≤ mk+1 или x ∈
∖ (m0, mn).
26. Написать программу возведения действительного числа в натуральную степень, используя рекурсивный "индийский алгоритм":
n x, если n = 1,
x =  n mod 2 [n/2] 2
Здесь [∙] – целаая часть числа.
∙(x ) , если n > 1.
x
27. Заданы 4 точки М1, …, М4 в пространстве, не лежащие в одной
плоскости, как вершины тетраэдра. Для произвольной точки Х
пространства решить, находится ли она внутри тетраэдра (в этом
4
4
случае Х = ∑k=1αkMk, ∑k=1αk = 1, все αk (0,1)).
28. Проверить формулы (до 5-го десятичного знака):
1) ln( x) = ∑
∞
1  x-1 2n-1

 , x > 0,
n=1 2n-1 x+1
2) - ln(1-x) = ∑
∞
xn
n=1
n
, x < 1,
3) - ln|sin(x)| = ln(2) + ∑
∞
n=1
cos(2nx)
n
, 0 < x < π,
180
∞
(x∙ln(a))n
4) a = 1 + ∑
,
n!
n=1
x
5) sin(x) = ∑
∞
6) cos(x) = ∑
7) x = 2∙∑
∞
n x2n+1
(-1) (2n+1)! ,
n=0
∞
n x2n
(-1) (2n)! ,
n=0
n-1 sin(nx)
(-1)
, -π < x < π,
n
2
∞
x
8) sin(x) = x П 1 - 2 2,
nπ
n=1 
2
∞
4x


9) cos(x) = П 1 2 2,
(2
n
-1)
π

n=1 
n=1
10) arctg(x) = ∑
11)
12)
13)
14)
15)
16)
∞
n x2n+1
(-1) 2n+1 ,
n=0
∞
ex + e-x
x2n
=
∑
,
2
n=0 (2n)!
∞
ex - e-x
x2n+1
=
∑
,
2
n=0 (2n+1)!
∞
π2 π
cos((2n+1)x)
- |x| = ∑
, |x| < 1,
8 4
(2n+1)2
n=1
∞
1 1+x 1
x4n+1
, -1 < x < 1,
 1-x  + arctg(x) = ∑
ln
4   2
n=0 4n+1
∞ (2n+1)x2n
2
(1+2x2)ex = ∑
,
n!
n=0
∞
cos(nx)
1 π2
- x2 = ∑ (-1)n n2 , 0.2π ≤ x ≤ π.

4 3

n=1
29. Определить тип переменной Person, содержащий фамилию, пол,
возраст, рост, вес, зарплату, количество детей и семизначный телефон. Определить массив из 10 – 15 переменных указанного типа.
Элементы массива заполнить следующим образом: фамилии ввести с клавиатуры, возраст (> 20 лет), рост (> 100 см.), количество
детей, зарплату и телефон (> 999999) определить случайным образом (функцией RND). Вес задать формулой: вес (кг) = рост (см) –
80. Вывести содержимое полученного массива, упорядочить массив по содержимому одного из указанных полей типа (по фамилии
– алфавитный порядок, по возрасту, весу и т. д. – в порядке возрастания).
30. Вычислить пределы или определить, что предела не существует:
x+1
2
2sin2(x) + sin(x) -1
 x -1  x-1
1) lim
,
2) lim  2  ,
2
x→∞ x +1
π 2sin (x)-3sin(x) +1
x→
6
π
sinx - 
3
3) lim
x→ 0
cos(x) - cos(x)
,
sin2(x)
4) lim
π
x→
3

3
1 - 2cos(x)
,
181
1+x
6) lim 

x→ 1 2+x
5) lim (sin( x+1) - sin( x)),
x→∞
x
1- x
1-x
,
2
ln(1+3x)
9) lim
x ,
x→ -∞ ln(1+2 )
22 - 2x
8) lim x 2 ,
x→ 2 2 - x
ln(1+3x)
10) lim
x ,
x→ +∞ ln(1+2 )
11) lim (1-x) logx(2),
1
12) lim x∙  ([∙] – целая часть),
1
x
7) lim (1-2x) ,
x→ 0
x
n!  e n
14) lim
  ,
n→∞ n n
x→ 1
x→ 0
13) lim sin2(π n2 + n),
n→∞
15) lim xn, где x1 = 5, xn = 5+xn-1, n>1,
n→∞
3x2 - 1
16) lim fn(x), где f1(x) = 2
, f (x) = f1(fn-1(x)), n>1.
x -x+1 n
n→∞
31. Построить график функции на указанном промежутке (вычисления
выполнять с точностью не меньше 0.00001).
∞
n
n
(-1) n!x
1) f(x) = ∑
, x  [-1, 1].
n = 0 (2+ 1)(2+ 3)...(2+ 2n+1)
∞
2) f(x) = ∑
n=0
n
(-1) n!
2
n2
∞
3) f(x) = ∑
n=1
2-
xn, x  [-1, 2].
xn
2 + 2 + … + 2 n2, x  [-1; 1].
(n слагаемых корней)
sin2 k 
1
4) f(x) = ∑ n x ∏
, x  [-2, 2],  =
.
2
2
n=1
3
k = 1 1 + x + cos k 
∞
∞
n
n
5) f(x) = ∑ (-1)n xn ∏ 2 n=1
k=1
k+1

3, x  (-1, 1).
∞
2n + 1
6) f(x) = ∑ (-1)n-1 sin 2 x , x  [-, ].
n=1
n (n + 1)
 n2 x
∞ cos
7) f(x) = ∑ 2 n 2+ 1 , x  [-2, 2].
n = 2 n ln n
∞
8) f(x) = ∑
ln (n!) n
x , x  [-1, 1].
n=1
n3
182
∞
9) f(x) = ∑
n sin n x
, x  [0.2, 4].
n = 1 (1 + x) (1 + 2x) … (1 + nx)
∞
10) f(x) = ∑
n=1
n2 n
(x + x –n), x  [0.5, 2].
n!
∞
11) f(x) = ∑
n=0
xn
n/ 
 2
∞
12) f(x) = ∑
sin nx
n=1 3
∞
13) f(x) =
∑
n=1
∞
!
4
n
 n 1
 x 
∑
- ln n   , x  [-1, 1].
k = 1 k
  2
n-1
n=1
∞
, x  [-, ].
4
n +x
14) f(x) = ∑ (-1)
15) f(x) = ∑
, где [ ∙ ] -целая часть числа, x  [-2, 2].
2n + 1
2n
 n
1 x
∑
 2 , x  [-1, 1].
k = 1 2k - 1 n
2
2
(n!) 2n
x , x  [-1, 1].
n = 0 (2 n + 2)!
∞
16) f(x) =
1
П (ln(n+x) – ln(n)) /n.
n=1
32. Массив записей из задания 29 сохранить в файле прямого доступа.
Выбрать из файла данные, удовлетворяющие определенному условию (например, фамилии, начинающиеся на заданную букву, либо
с зарплатой не ниже заданной, либо с числом детей больше трех и
т. д.).
33. Организовать в VBA (Excel, используйте вставку рисунка с дверкой по ситуации) диалог типа:
 "Сантехник"  "Не вызывали!"
"Тук-тук!"  "Кто там?"   "Красная Шапочка"  "Заходи!"
 "Серый Волк"  "Пшел вон!" .
При приглашении "Заходи" дверке следует открыться.
34. Работа с таблицей Excel (автозаполнение, вычисление по формулам): заполнить таблицу значений xn = n h, yn = 5 sin xn + 2СлЧис-1,
n = 0, 1, …, 10, с шагом h = 0.2. Заполнить таблицы значений xn2,
xn yn . В конце каждой таблицы посчитать среднее значение с помощью меню и встроенных функций. Посчитать коэффициент (пар-
183
xy
¯ - x̄ ȳ
(чертой обозначено среднее значение)
x¯2 - x̄ 2
и свободный член b = ȳ - k x̄. Заполнить таблицу значений парной
регрессии Yn = k xn + b. Построить сравнительную диаграмму значений yn и Yn .
35. Элементы управления в Excel: построить модель калькулятора с
вычислением основных элементарных функций.
36. Элементы управления в Excel: создать программу чтения информации из текстового окна с занесением ее в в окно списка и выбора
строки списка (мышкой) с занесением информации в текстовое окно. В окне списка информация не должна повторяться. Попробуйте
вносить информацию в список, не нарушая (алфавитного) порядка.
37. Excel: постройте макрос (запускаемый кнопкой на рабочем листе),
заполняющий таблицу значений функции из задания 31 и рисующий на этом же листе график по таблице значений.
38. Составить в Excel диалоговое окно по выбору маршрута в турагенстве, предлагающем варианты маршрутов, информацию о наличии
мест, виде транспорта, стоимости, бронировании отеля.
39. Даны коэффициенты многочленов Pm(x) = p0 + p1x + … + pmxm, Qn(x)
= q0 + q1x + …+ qnxn. Найти коэффициенты произведения многочленов Pm(x)Qn(x) = c0 + c1x + …+cm+nxm+n.
40. Решите в Excel систему уравнений из задания 60.
41. Решить в Excel задачу при указанных ограничениях:
1) min (3x-7y+2z) при x≥0, y≥0, z≥0 и
x+y-z ≤ 6, -x+4y ≤ 3, y+2z ≥ 1, x-y-z = 4;
2) min (6x-y+3z) при x≥0, y≥0, z≥0 и
5x+3y-6z ≤ 10, 5x-9y+7z ≤ 0, x+7y+7z ≤ 25, 2x+2y+9z = 18;
3) min (7x-5y+9z) при x≥0, y≥0, z≥0 и
x+9z ≤ 18, 9x-4y-z ≤ 20, -7x+y+5z ≥ 5, -x+y+9z = 21;
4) min (x+4y+8z) при x≥0, y≥0, z≥0 и
7x-8y+5z ≤ -2, x+7y ≥ 2, 4x+9y+7z ≤ 7, 5x+9y+2z = 5;
5) max (3x+5y+9z) при x≥0, y≥0, z≥0 и
-x+7y+5z ≤ 12, 7x-y-8z ≥ 10, -3x+5y+9z ≤ 18, 3x+8y-5z = 5;
6) max (-8x+9y+8z) при x≥0, y≥0, z≥0 и
9x-8y+z ≥ 10, 6y-5z ≤ 5, 8x+7y+3z ≥ 20, x-4y-z = 15.
42. В Excel с помощью теоремы Ферма определить точки возможного
экстремума, определить тип экстремума (если он есть):
ной) регрессии k =
1) f(x) = - x12 + 2 x1 x2 – x22 – 4 x32,
2) f(x) = x13 + x22 + x32 + x2 x3 – 3 x1 + 6 x2 + 2,
3) f(x) = - x12 – x22 –x32 – x1 + x1 x2 + 2 x3 ,
184
4) f(x) = (x1 – 1)4 + 10 (x2 – x1)2 + 3 (x3 – x22)2 ,
5) f(x) = - x12 + 2 x1 x2 – x22 – 4 x32 + 4 x2 x3 ,
6) f(x) = x12 + 2 x22 – 3 x32 – 6 x1 x2 + 8 x1 x3 – 4 x2 x3 ,
7) f(x) = x13 – x1 x2 + x22 – 2 x1 + 3 x2 – 4 ,
8) f(x) = 2 x13 +4 x1 x22 – 10 x1 x2 + x22 ,
9) f(x) = 10 (x1 – 2)2 + (x2 – x12)2 + (x3 – x22)2 + (x4 – x32)2 ,
10) f(x) = (x2 – x12)2 + (1 – x12)2 + 10 (x1 + x2)2 ,
11) f(x) = 3 x1 x2 – x1 x22 – x12 x2 ,
12) f(x) = x14 + x24 – (x1 + x2)2 ,
13) f(x) = x12 + 5 x22 + 3 x32 + 4 x1 x2 – 2 x2 x3 – 2 x1 x3 ,
14) f(x) = - x12 - 2 x1 x2 + x22 + 2 x1 x3 - x2 x3 - x32 + 4 x1 - 2 (x2 - x3) ,
15) f(x) = 4 x1 x2 – x1 x3 + 2 x2 x3 + x22 + 2 x32 – 3 x1 + x3 ,
x
x
x
x
x
x
16) f(x) = x1 + x2 + x3 + x4 + x3 + x2 (x > 0).
2
3
4
3
2
1
43. В Excel решить задачу на экстремум с ограничениями:
1)
min x12 + x22 - x3
 x22 - x1 = 3

 x1 ≥ 0, x2 ≥ 0, x3 ≤0 .
3)
max x2 + x32
 x1 - x22 + x1 x3 = 0
 2
2
2
 x1 + 2 x2 + 3 x3 ≤ 4 .
5)
7)
9)
min x12 + x1 x2 - 2 x22 + x1
 x1 - x2 = 1
 2
2
 x1 + x2 ≤ 1 .
1
min 2 [(x1 - )2 + x22]
  x22 = x1

≥0 .
max x2 - x3
 x12 + x22 +x32 = 9

 x2 + x3 ≤ 0 .
2)
max x1 - 3x2
 x12 + x22 - 2 x1 x2 = 0

 x1 + x2 ≥ 0 .
4)
max x12 + x22 - 3 x1 x2
 (x1 - 1)2 + x22 = 4

 x2 ≥2 .
6)
max x12 + x22 + x32
 x12 + x22 - x3 = 0

 x1 + x2 + x3 ≤ 4 .
8)
min 2 x12 - x1 x2 + x22 + x3
 x1 = x3

2
 x2 + x3 ≤ x1 .
10)
extr (x1 - 2)2 + (x2 - x3)2 - 4 x1 x2
 x1 + x2 + x3 = 3
 2
 x1 ≤ 2 x2 - x3 .
185
extr (x1 - )2 + (x2 + )2
2
2
11)  x1 + x2 = 4

 x1 + x2 ≤ ,  ≥ 0 .
min x12 + x22 + x32
13)  x1 + x2 + x3 = - 4
 x1 + 3 x2 ≥ x3 ≥ 0 .
min x3
2
2
x
1 = x2 ,

15)  x 2 + x 2 + x 2 ≤ 9,
 1 2 3
 2 x1 + x3 ≥ x2 ≥ 0 .
extr x12 + (x2 - 2)2 - 4 x2 x3
12)  x1 + x2 + x3 = 4
2
2
 x1 + x2 ≤ 1, x1 ≥ 0, x2 ≥ 0 .
14)
min x1 + x22
 x12 + x22 + x32 = 4

 0 ≤ x3 ≤ 2 x1 - x2 .
16)
max x12 + x22 - 12x1 - 16x2
2
2
x1 + x2 ≤ 25,

x1 ≥ x2 + 1 .
44. Word: составить документ, поясняющий суть теоремы Пифагора.
Документ должен содержать заголовок, пояснение важности темы,
цветной рисунок с необходимыми обозначениями (чертеж), текст
теоремы в классическом и векторном вариантах. Использовать таблицу с невидимой рамкой для совмещения рисунка и текста.
45. Word: вставить в текстовый документ формулу вида:
d(x, y, z)
I = ∫∫∫ F(x(u,v,w), y(u,v,w), z(u,v,w)) d(u, v, w) du dv dw, где
(u,v,w)Ω'
 x x x 
d(x, y, z)  u v w 
d(u, v, w) =  y y y  - якобиан преобразования координат, и
 u v w 
альтернативу
46. Word: в документе фразе "заполнить таблицу" назначить макрос,
заполняющий подготовленную таблицу значениями функции из
задания 31 (11 значений функции на указанном промежутке) и рисующий в документе график по этим значениям.
47. Создать документ, при открытии которого появляется требование
ввода пароля. Если пароль верный, документ готов к работе, в противном случае документ автоматически закрывается.
48. Web: составить документ на тему о своей семье. Документ состоит
из двух вертикальных половин: в левой – списочный состав семьи,
в правой – информация, появляющаяся при щелчке мышкой по
элементу списка в левой части.
49. MathCad: вычислить пределы из задания 30.
186
50. MathCad: вычислить значение lim
a+0
 -adx 2 dx
  x +  x .
 -1

a
51. MathCad: для функции из задания 31 найти производную в средней точке промежутка, вычислить интеграл от этой функции по заданному промежутку, построить график функции и касательной к
графику в средней точке промежутка.
x + fn - 1 (x)
52. MathCad: функция f0(x) ≡ 1, а fn (x) =
, n = 1, 2, …., x > 0,
2 fn - 1(x)
функция F(x) = lim fn (x). Построить график функции F и ее проn∞
изводной.
53. MathCad: решить систему линейных уравнений Ax = b с матрицей
1 2 3 4
10
2 4 3 1
10
A = 3 4 1 2 и правой частью b = 10 методом Крамера и


 
4 3 1 2
10
методом Гаусса. Сравнить результаты. Могут ли появиться проблемы с реализацией метода Гаусса?
54. MathCad: для фиксированного натурального n определить матри 4, если i = j,

цу Ai, j =  1
(i, j = 0, 1, …, n-1) и вектор с длины n,
при
i
≠
j
 i - j
первые координаты которого – цифры номера студенческого билета. Пусть b = A∙c. Решить систему линейных уравнений Ax = b:
а) с помощью встроенной функции Lsolve, б) методом обратной
матрицы, в) методом Крамера, г) методом Гаусса. Сравнить результаты с номером студенческого билета.
55. MathCad: для функции f(x) построить график, определить область,
содержащую наименьший по модулю отличный от нуля корень,
найти значение этого корня с шестью верными знаками методом
деления пополам и методом Ньютона.
1
1) f(x) = 2 2 - tg x + 2;
2) f(x) = arctg x - e-x – 1.5;
4x - 
x  50
x+3

3) f(x) = 1 -  - e -x + 0.05; 4) f(x) = x + x2 - 9 - 2
;
50
(x - 3)2

1
x2
5) f(x) = e arctg x – 8;
7) f(x) = sin 2x – arctg x;
9) f(x) = 1.6 e
- 12
x
- arctg x;
6) f(x) = x 2.1 - x2 – 1;
8) f(x) = cos x + x2 – 1.2;
x2
10) f(x) = ch x + 1 – 2 ;
187
1
11) f(x) = x + - tg (x – 1);
x
13) f(x) =
3
12) f(x) = ln (1 + x) - x - 10;
x - 4x + 9 – 3 cos x 5 – 0.01;
4
2
/
x
x
14) f(x) =  e - 2;
 
x 1
15) f(x) = x + 1 – 10 ln (1 + x + 1); 16) f(x) = ctg x + - .
2 x
56. MathCad: для фиксированного натурального n определим функx
цию непрерывной дробью f(x) = 1 - x +
. Провести
x
2+
3+
x
+
n+x
средствами MathCad полное исследование функции (найти корни,
асимптоты, корни первой и второй производной, промежутки монотонности, экстремумы, перегибы), сравнить с построенным графиком.
57. MathCad: исследовать на экстремум функции из задания 42.
58. MathCad: найти экстремум в задачах п. 43.
59. MathCad: для приведенных ниже интегралов вычислить значение с
тремя верными знаками по формулам прямоугольников, трапеций
и Гаусса (с двумя узлами), сравнить с результатом интегрирования
MathCad. Точность можно оценить, увеличивая (например, удваивая) число узлов разбиения промежутка интегрирования.
1 sin x
1
1 cos 1 
1
 /x
1) ∫ ln x (x - 1) dx; 2) ∫x ln x dx; 3) ∫
dx;
 
0
0
0
x
1
1
1
x dx
dx
 1  dx
4) ∫
5) ∫cos x2 ; 6) ∫
;
4;
  x
0 1-x
0
0 (2 - x) x (1 - x)
1
1 ln x dx
1
2
sin3x
1 x + x

7) ∫
dx; 9) ∫ 1 + x -  e
dx;
1; 8) ∫

0
0 x ln x
0.5 
x
ln 1 + 
x

3
1  e x

x
x sin x
10) ∫arcsin
12) ∫x dx;
2 dx;
1 + x dx; 11) ∫
0
0  
0 1 + cos x
 /2

x dx
13) ∫
;
0 1 - sin x
 /2
14)
2
dx
 - 2x
∫
dx; 15) ∫ x ln x;
0.5
0 ln sin x

/2
2
x dx
ln (sin x)
16) ∫
dx; 17) ∫ ctg x dx; 18) ∫
.
(x - 1) (2 - x)
x
-  /4
1
0
60. MathCad: найти приближенное решение системы уравнений методом Ньютона, сравнить с результатом, полученным средствами пакета.
188
2
2
2
1)
 x - 3xy + y + 2yz - xz -z = 4,
2
2
2
x +y =z ,
 2x + 3y = z + 1 ,
старт в точке (1, 1, 1),
2)
 3x + 1.5y + z = 5,
 6xyz - x + 5y + 3z = 0,
 x (5x - y) = 1, старт в точке (1, 0, 0),
3)
 x - 4y + xzt + t = 13,
 x(x ++ 2y1) + zy = t,y - z - 1
 t +1 + t = y .
2
2
2
26 (xyzt + xyz + xt + z) + 23 (yzt + yz + t) = 0,
2
2
3
2
2
2
2
2
2
Попробуйте различные точки старта, например, (0, 1, 1, 1)
или (0, 1, -2, 1).
 x - 3 z + t = yz + 5,
(x - t) + z = 1,
 yln (tx
+ y) = z,
 x + y + z + t = 2 , старт в точке (1, 1, 1, 0).
y
4)
2
Попробуйте другой старт, например, (1, 1, 1, 1).
 x 
5)
 sin y + 1 = 2 (cos(tx) - t),
x + y + z = 2t ,
 x + t = yt,
 y + z + t
xy + yz + zt + tx = 2, старт в точке (1, 0, 1, 0).
6)
2 + 3 = 5 ,
y
y
z
2 + 3 = 5 ,
2z + 3z = 5x, старт в точке (2, 0, -1).
7)
x + y + z = 14,
xy + xz + yz = 11,
xyz = 6, старт в точке (0, 2, -1).
8)
+z
= 512,
x
 ylog (x) + xlog (y) = 8,
 zlog (y) + ylog (z) = 2 2, подберите стартовые значения.
2
2
2
x
x
y
3
2
2
logy(z)
2
logy(x)
z
z
x
x
61. MathCad: в матрице А найти два столбца, угол между которыми
(как векторами) минимальный.
62. MathCad: разложить заданный вектор по столбцам данной матрицы.
189
63. MathCad: найти расстояние между двумя прямыми
x y+1 4-u v-2
y z+3 u v+7
=
=
=
, z = -1 и =
=
=
, x = 5.
3
1
2
7 -2
4
2
3
64. MathCad: найти проекцию вектора p = (3, -1, 1, 4, 1)T на первую
прямую предыдущего задания.
65. MathCad: для заданной положительно определенной матрицы А
вычислить С = A с точностью ε, для каждого k ≥ 1 решая отно2
сительно Ck уравнение 2∙Сk-1Ck= (Ck-1+A), k = 1, 2, …, где C0=E –
единичная матрица. Итерации заканчиваются при выполнении
неравенства ||Ck – Ck-1|| ≤ ε (здесь можно взять ||C|| = max |Ci,j|).
i,j
66. MathCad: определить тип кривой, заданной уравнением х2 - 6ху
+ 3у2 = 1, построить график линии в собственных осях.
67. MathCad: построить график ленты Мëбиуса, заданной параметриx = cos(u)(1+v∙cos(u)),
чески y = sin(u)(1+v∙cos(u)), u (-π, π), v (-0.2, 0.2).
z = v∙sin(u),
68. MathCad: найти ближайшее к началу координат решение системы
x-2y+z+t-u = 4,
уравнений 
-3x-y-z+3t+2u = 3.
69. MathCad: найти решение задачи Коши x''(t) - tx'(t) + x(t)2 = 0, x(0) =
= 1, x'(0) = -0.7, построить график в плоскости (x,t) и в фазовой плоскости.
70. MathCad: для решения уравнения из предыдущего задания найти
значение x'(0) при условии х(0) = х(2) = -1 (краевая задача).
71. MathCad: решить краевую задачу для ОДУ y''(x) - 2x∙y'(x) +
+ y(x)∙|y(x)| = 0, x [0, 3], y(0) = 2, y(2) = -10.
y''(x)-z'(x)+y(x) = 2∙cos(x),
72. MathCad: привести систему уравнений 
-x
z'''(x)+x∙y(x) = e
к нормальному виду и найти ее приближенное решение на промежутке [0, 3] при условиях y(0)=0, y'(0)=1, z(0)=-1, z'(0)=z''(0)=0. Построить график решения (по 200 точкам).
73. MathCad: для фиксированного n (>1) найти встроенными средстваx +1, если i < n,
ми решение системы уравнений xi + xi2+…+xin =  i+1
x1+1, если i=n,
i = 1, …, n, взяв в качестве начального значения xi =1, i.
74. MathCad: решить при дополнительном ограничении уравнение
cos2(xy) - 3sin(xy)cos(xy) = 2cos(y)cos(2xy-y)-2cos2(xy-y),
 3
x + 2xy ≤ 5, старт в точке (-1, 1).
75. MathCad: для функции f(x) = |x|, заданной на [-1, 1] значениями в
n = 20 точках (с постоянным шагом) подобрать наилучший в смысле МНК многочлен четвертой степени.
190
ЛИТЕРАТУРА
1. Абрамов В.Г. Задачи по программированию. / В.Г. Абрамов.- М.,
1988.
2. Андерсон Е. Visual Basic, шаг за шагом. / Е. Андерсон. -М., 1998.
3. Зельднер Г.А. Программируем на языке Quick Basic 4.5. / Г.А. Зельднер. -М., 1996.
4. Могилев А.В. Информатика. / А.В. Могилев, Н.И. Пак, Е.К. Хеннер. –М., 2003.
5. Наварро Э. XHTML: учебный курс. / Э. Наварро. -Санкт-Петербург, 2001.
6. Охорзин В.А. Прикладная математика в системе MATHCAD. Учебное пособие./В.А. Охерзин. –СПб.: Лань, 2009.
7. Очков В.Ф. MathCad 14 для студентов и инженеров. /В.Ф. Очков. –
СПб.: BHV, 2009.
8. Симонович С. Занимательное программирование на Visual Basic.
/ С. Симонович, Г. Увсеев. -М., 2004.
9. Соколов А.Н. Программирование в среде Excel Visual Basic: методические указания по курсу "Информатика". / А.Н. Соколов. –
Калининград, 2000.
10. Microsoft FrontPage 2002, шаг за шагом: практическое пособие. М.: ЭКОМ, 2002.
11. Microsoft Excel 2003. -Санкт-Петербург: "БХВ-Петербург", 2004.
191
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автозаполнение 91
алгоритм Эвклида 6
альтернативный блок 28
арифметическое выражение 12
Базы данных 123
− − в Access 126
− − в Excel 125
байт 4
бит 3
блок-схема 6
Вставка автофигур 109
− диаграммы 101
− закладки 114
− надписи 109
− полей 110
− таблиц 115
− формул 110
− функций 90
выбор безусловный 23
− по условию 23
выход из функции 22
вычисление произведений 40
− сумм 39
− пределов 43
− приближенные 43
вычисления в Excel 103
Графика 67
− в Excel 98
графики в Mcd 138
Двоичное дерево 82
двоичный выбор 58
динамическое распределение памяти 79
дифференцирование на сетке 165
− приближенное 153
Знаки арифметические 9
знаки сравнения 9, 25
Идентификатор 10
иерархия в Excel 73, 85
имя 10
инструкция ByRef 21
инструкция ByVal 21
− Do 29
− Loop 29
− Option Base 53
− Option Explicit 82
− Public 76
− Randomize 14
− Static 37
− Type ... End Type 55
− Until 30
− определения константы 13, 14
− − массива 45
− − объекта 73
− − подпрограммы 22
− − строки 16
− − типа 13
− − функции 21
интерполяция 164
итерации 76
Классы 76
− , создание 77
коды ASCII 18
коллекции, свойства 83
комментарий 11
константа ORIGIN 48
− vbCrLf 85
− vbNewLine 85
− wdToggle 119
константы 14, 136
конструктор 92
Макрос 22
макросы в таблицах 117
массивы 45
меню "Вставка функций" 15, 104
− "Калькулятор" 15
− анализа 51, 142
− вставки формулы 116
− диаграмм 68, 69
− логических сравнений 25, 143
− матричных операций 27
− назначения макроса 75
− настройки метода 169
− отладки 69, 72
− "Подбор параметра" 106
192
меню "Поиск решения" 107
− программирования 25
− рабочего листа 86
− свойств автофигур 74, 100
− символьных вычислений 140
− трассировки 71
− элементов управления 92
метка 11
метод Гаусса 61
− Рунге-Кутты 166
− спуска 172
− штрафов 173
− Эйлера 166
методы 77
многочлен Лагранжа 163
многочлены Гаусса 161
Объект UserForm 94
объекты, свойства 73, 76
оператор Add Line 28, 31
− break 52
− Close 63
− Do ... Loop 29, 52
− End 63
− Exit 22, 30
− For ... Next 29, 31, 52
− For Each ... In ... Next 53, 56, 83
− Get 64
− Given 143, 144, 167
− GoTo 23
− If 28
− Input 62
− Kill 63
− LineInput 63
− MsgBox 19
− New 82, 83
− On Error 70, 72
− Open 62, 64
− otherwise 28
− Print 63, 70
− Put 64
− Redim 46
− Resume Next 70
− return 22, 28, 31
− Select Case 28
− Set 73
− Trace Error 71
− While ... Wend 29
оператор With ... End With 55, 56
− Write 63
− альтернативного выбора 28
− векторизации 51
− вычисления 12
− градиента 153
− перехода 23
− присваивания 12
− ранжирования 31
− условный 23
− цикла 29
операторы Mcd 136
− ввода 19
− вывода 19
операции сравнения 24
определение массива 47
− типа пользователя 54
определенный интеграл 161
− – , рекурсии 162
Параметры страницы 108
− , область видимости 22
перевод в другую систему счисления 34
подпрограмма, определение 22
программа 11
продолжение строки операторов 20, 24
Разветвление 23
разделители 9
рекурсии 37, 79
Символы специальные 9
система счисления двоичная 4
системы линейных уравнений 145, 154
− − − , метод прогонки 157
− нелинейных уравнений 158, 160
− − − , метод Ньютона 158
− − − , − секущих 58
слово служебное 10
события 76
создание Web-ссылок 130
− − таблиц 130
− макросов автоматическое 75
сортировка 57
ссылка абсолютная 90
− относительная 90
строка 10, 15
структура языка 10
193
Стэки 53
Таблица истинности 24
тактовая частота 4
тип String 64
− Variant 38, 53, 54
− данных 13
типы 136
− , переопределение 14
тэги 128, 129
Условный блок 25
условный оператор 28
Файлы 62
− бинарные 63
− в Mcd 151
− последовательного доступа 62
− прямого доступа 64
фрейм 133
функции Mcd 136
− аргументы 21
− векторов и матриц 145
− вставка 15
− встроенные 14
− для решений ОДУ 148
− логики 24
− обработки строк 16
− определение 21
− оптимизации 143
функция ABS() 14
− appendprn 66
− Array() 53
− ASC() 16
− ATN() 14
− augment() 48, 61
− Chr() 16
− Chrw() 119
− cols() 48
− concat() 16
− CreateMesh() 139
− csort() 57
− Eof() 63
− Find() 147
− Fix() 14
− Format() 16
− geninv() 48, 62
− Hex() 16
− identity() 51
функция InputBox() 19
− Instr() 16
− last() 48
− Lcase() 16
− Left() 16
− Len() 16
− Loc() 63
− Log() 14
− lsolve() 48, 62
− Mid() 16
− Minerr() 150, 161
− Minimize() 144
− Mod 14
− MsgBox() 24, 85
− num2str() 16
− pause 72
− polyroots() 106
− readprn() 66
− Right() 16
− Rnd 14
− rows() 48
− rsort() 57
− seek 108
− Sgn() 14
− sign() 34
− sort() 48, 57
− Sqr() 14
− stack() 48, 60
− Str() 16
− str2num() 16
− str2vec() 16
− String() 16
− strlen() 16
− submatrix() 48
− substr() 17
− Tan() 14
− Timer 32
− trace 72
− Trim() 16
− trunc() 17
− Ubound() 17, 52,53
− Ucase() 16
− Val() 16
− vec2str() 17
− writeprn() 65
− конкатенации 16
− ЛИНЕЙН 105
− МОПРЕД 49
− МУМНОЖ 49, 107
194
Функция РАНГ 105
− СМЕЩ 106
− ТРАНСП 107
− условная if() 24
Цикл безусловный 29
− пересчета 29
циклы 29
− с условием 29
Числа 13
− Армстронга 36
число 10
Элементы управления 91
− − , свойства 93
Ячейки рабочего листа 88
− − − , свойства 88
195
ОГЛАВЛЕНИЕ
Bведение ....................................................................................................... 3
1. Общая часть.............................................................................................. 9
1.1. ОСНОВНЫЕ СТРУКТУРЫ.............................................................. 9
1.2. ОСНОВНЫЕ ТИПЫ ........................................................................ 13
1.2.1. Числа........................................................................................... 13
1.2.2. Строки........................................................................................ 15
1.3. ОПЕРАТОРЫ ВВОДА И ВЫВОДА .............................................. 19
1.4. ФУНКЦИИ И ПОДПРОГРАММЫ................................................ 21
1.5. РАЗВЕТВЛЕНИЕ И АЛЬТЕРНАТИВА ........................................ 23
1.5.1. Безусловный выбор ................................................................... 23
1.5.2. Условный выбор ........................................................................ 23
1.5.3. Альтернативный выбор .......................................................... 28
1.6. ЦИКЛЫ ............................................................................................. 29
1.7. МАССИВЫ....................................................................................... 45
1.7.1. Программные стэки ................................................................ 53
1.7.2. Тип пользователя .................................................................... 55
1.7.3. Сортировка массивов.............................................................. 57
1.8. ФАЙЛЫ ............................................................................................ 62
1.8.1 Файлы в VBA .............................................................................. 62
1.8.2. Файлы в Mcd .............................................................................. 65
1.9. РАБОТА С ГРАФИЧЕСКОЙ ИНФОРМАЦИЕЙ......................... 67
1.10. ОТЛАДКА И ТРАССИРОВКА .................................................... 69
1.11. ОБЪЕКТНО-ОРИЕНТИРОВАННАЯ ИДЕОЛОГИЯ ................ 72
1.12. КЛАССЫ ........................................................................................ 76
1.12.1. Собственные классы ............................................................. 77
1.12.2. Коллекции ............................................................................... 83
2. Элементы Excel ...................................................................................... 84
2.1. РАБОЧИЙ ЛИСТ ............................................................................. 86
2.2. ЯЧЕЙКИ ........................................................................................... 88
2.3. ЭЛЕМЕНТЫ УПРАВЛЕНИЯ........................................................ 91
2.4. ГРАФИЧЕСКИЕ СРЕДСТВА ........................................................ 98
2.5. ВЫЧИСЛЕНИЯ ............................................................................ 103
3. Работа в WORD.................................................................................... 108
3.1. ОБЩЕЕ РЕДАКТИРОВАНИЕ ..................................................... 108
3.2. ВСТАВКИ....................................................................................... 109
3.2.1. Графические объекты ........................................................... 109
3.2.2. Поля и ключи ........................................................................... 110
3.2.3. Закладки ................................................................................... 114
3.3. ТАБЛИЦЫ ...................................................................................... 115
3.4. ГРАФИКА ...................................................................................... 120
4. Базы данных ......................................................................................... 123
196
5. Гипертекстовая разметка .................................................................... 128
5.1. ОСНОВНЫЕ ТЭГИ HTML .......................................................... 129
5.2. ФОРМАТИРОВАНИЕ ТАБЛИЦ ................................................. 130
5.3. ФРЕЙМЫ ........................................................................................ 133
6. Элементы вычислений в Mсd ............................................................ 136
6.1. КРАТКИЙ ОБЗОР ......................................................................... 136
6.2. НЕКОТОРЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МОДЕЛИ ....................... 154
6.2.1. Системы уравнений .............................................................. 154
6.2.1.1. Системы линейных уравнений ......................................... 154
6.2.1.2. Нелинейные уравнения и системы ................................... 158
6.2.2. Определенный интеграл........................................................ 161
6.2.3. Функции на дискретном множестве ................................. 163
6.2.4. Обыкновенные дифференциальные уравнения .................. 166
6.2.5. Минимизация функций......................................................... 169
6.2.5.1. Функции одной переменной ............................................. 169
6.2.5.2. Функции многих переменных .......................................... 171
6.2.5.2.1 Задачи без ограничений................................................ 171
6.2.5.2.2. Задачи с ограничениями .............................................. 172
6.2.6. Pазностная модель и прогноз ............................................... 173
Задания...................................................................................................... 176
Контрольные вопросы .......................................................................... 176
Контрольные задачи ............................................................................. 177
ЛИТЕРАТУРА ......................................................................................... 190
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ ............................................................... 191
197
Игорь Александрович ПАХНУТОВ
ИНФОРМАТИКА
с элементами программирования
Учебное пособие содержит основной материал для проведения
учебных (как лекционных, так и лабораторных) занятий по курсу
"Информатика", предназначено студентам младших курсов технических вузов и университетов. Материал курса расчитан на два семестра
аудиторной работы и включает некоторые разделы информационных
технологий. Материал пособия предполагает знакомство с базовыми
понятиями предмета в объеме стандартной школьной программы.
На первой странице обложки: Аугуста Ада Кинг, урожденная
Леди Байрон (1815-1852), "первый в мире программист" (A.E. Chalon,
1838).
Редактор Л.И. Полищук
УОП КГТУ. Заказ
. Тираж 50 экз.
Объем 6,2 п.л.; 6,9 уч.-изд. л.
Цена договорная