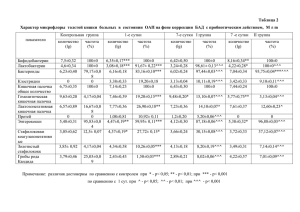
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА (НИУ) ИМЕНИ И.М. ГУБКИНА Кафедра разработки и эксплуатации нефтяных месторождений Домашнее задание по дисциплине «Осложненные условия разработки и эксплуатации нефтяных месторождений» Тема: «Решение задачи по методике расчета предельных безводных и безгазовых дебитов, предельной депрессии» Выполнила: студентка группы РН-15-05 Судакова О.И. Проверил: д.т.н., профессор Кучумов Р.Я. Москва, 2019 Вариант 1. Задание: Рассчитать одновременно предельный безводный и безгазовый дебит и предельную депрессию при разработке нефтегазовой залежи или нефтяной оторочки. Исходные данные Условный радиус контура питания 𝑅0 = 220 м; Нефтенасыщенная толщина пласта h=25 м; Разности плотностей нефти, газа и воды: кг ∆𝜌1 = 𝜌н − 𝜌г = 735 3 ; м кг ∆𝜌2 = 𝜌в − 𝜌н = 165 3 ; м Вязкость нефти в пластовых условиях 𝜇н = 5,1 ∗ 10−3 Па ∙ с = 0,00052 кг∙𝑐 м2 ; Горизонтальная проницаемость пласта Кг = 0,37 ∗ 10−12 , м2 ; Анизотропия пласта 𝜘 = 3; Радиус скважины 𝑟𝑐 = 0,1 м; Интервал вскрытия нефтенасыщенного пласта в безразмерных параметрах: 𝛼 = 0,2; 𝛽 = 0,7; Плотность перфорации m=10 отв/м; Глубина пулевого канала 𝑙0 = 0,28 м; Радиус пулевого канала 2𝑟0 = 0,013 м. Решение 𝑅0 220 1. Параметр размещения скважин: 𝜌0 = 2. При заданных параметрах 𝛼, 𝛽, 𝜌0 из таблицы находим плотности расходов 𝑞1 , 𝑞2 . 𝑞1 (α, β) = 𝑞1 (0,2; 0,7) = 0,075; 𝑞2 (α, β) = 𝑞2 (0,2; 0,7) = 0,153. 2 𝜘ℎ = 3∗25 = 2,93. Находим предельные безводную и безгазовую плотности дебитов: 3. 𝜀ℎ = 2𝜋Кг 𝑔ℎ = 𝜇н 2∗3,14∗3,7∗10−13 ∗9,81∗25∗86400 0,00052 = 0,095; 𝑞01 = 𝑞1 ∆𝜌1 𝜀ℎ = 0,075 ∗ 735 ∗ 0,095 = 5,22 𝑞02 = 𝑞2 ∆𝜌2 𝜀ℎ = 0,153 ∗ 165 ∗ 0,095 = 2,39 м2 сут ; м2 сут . Выбираем наименьшее значение из получившихся, чтобы 4. обеспечивался дебит одновременно безводный и безгазовый. 𝑞0 = min(𝑞01 , 𝑞02 ) = min(5,22; 2,41) = 2,39 м3 сут м − одновременно безводная и безгазовая плотность дебита скважины. Одновременно безводный и безгазовый дебит скважины: м3 𝑄 = 𝑞0 (𝛽 − 𝛼)ℎ = 2,39 ∗ (0,7 − 0,2) ∗ 25 = 29,88 . сут 5. По исходным параметрам 𝛼 и 𝛽 определяем ординату нейтральной линии тока 𝜉 ∗ (𝛼, 𝛽). Вычисленные значения безразмерной ординаты нейтральной линии тока ξ* как функции параметров 𝛼 и 𝛽 приведены в таблице ξ*=0,44 Рассчитываем величины относительных вскрытий ̅̅̅ ℎ1 , ̅̅̅ ℎ2 и 6. безразмерные параметры 𝜌01 , 𝜌02 : ̅̅̅1 = 𝜉 ℎ ∗ −𝛼 𝜉∗ = 0,44−0,2 = 0,545; 0,44 ∗ 𝛽−𝜉 0,7−0,44 ̅̅̅ ℎ2 = = = 0,464; ∗ 1−𝜉 𝜌01 = 𝜌0 𝜉∗ 1−0,44 = 𝜌0 2,93 0,44 = = 6,67; 2,93 𝜌02 = 1−𝜉 ∗ 7. По Таблице определяем значения функций 𝜓(𝜌𝑖 , ℎ̅𝑖 ): 1−0,44 = 5,24. ̅̅̅1 ) = 1,401; 𝜓(𝜌01 , ℎ 𝜓(𝜌02 , ̅̅̅ ℎ2 ) = 1,61; 3 ̅̅̅1 ) = 1,335; 𝜓(𝜌02 , ℎ 𝜓(𝜌01 , ̅̅̅ ℎ2 ) = 1,714. Определяем фильтрационные сопротивления 8. С1 (𝜌01 , ̅̅̅ ℎ1 ), С2 (𝜌02 , ̅̅̅ ℎ2 ), С2 (𝜌01 , ̅̅̅ ℎ2 ), С1 (𝜌02 , ̅̅̅ ℎ1 ): 𝛼 𝑅0 𝜉 ∗ 𝜓(𝜌01 , ̅̅̅ ℎ1 ) С1 (𝜌01 , ̅̅̅ ℎ1 ) = ∗ [ln ( ) − ] 𝜉 −𝛼 𝑟𝑐 𝛼 = 0,2 220 0,44 ∗ 1,401 ∗ (ln ( )− ) = 3,845; 0,44 − 0,2 0,1 0,2 1−𝛽 𝑅 1−𝜉 С2 (𝜌02 , ̅̅̅ ℎ2 ) = [ln ( 0) − ∗ 𝛽−𝜉 𝑟 𝑐 1−0,44∗1,61 1−0,7 0,2 1−𝛽 ]= 1−0,7 220 (ln ( 0,1 ) − 0,7−0,44 ) = 7,759; 𝛼 С1 (𝜌02 , ̅̅̅ ℎ1 ) = 0,44∗1,335 ∗ 𝜓(𝜌 ,ℎ 02 ̅̅̅̅ 2) 𝑅 [ln ( 0) − 𝜉 ∗ −𝛼 𝑟 ̅̅̅̅ 𝜉 ∗ 𝜓(𝜌02 ,ℎ 1) 𝑐 𝛼 ]= 0,2 0,44−0,2 220 ∗ (ln ( 0,1 )− ) = 3,966; 1−𝛽 𝑅 1−𝜉 С2 (𝜌01 , ̅̅̅ ℎ2 ) = [ln ( 0) − ∗ 𝛽−𝜉 𝑟 𝑐 1−0,44∗1,714 1−0,7 9. ∗ 𝜓(𝜌 ,ℎ 01 ̅̅̅̅ 2) 1−𝛽 ]= 1−0,7 220 (ln ( 0,1 ) − 0,7−0,44 ) = 7,935. По формулам подсчитываем фильтрационные сопротивления С01 и С02 : 1 4𝑟𝑐 ℎ1 𝑙0 С01 = ̅̅̅̅ (ln ( 𝜘 1 0,1 3 ) − 𝑚𝑙 ln(2𝜋𝑟0 𝑚)) = 0,55 ∗ (ln (4 ∗ 0,28) − 10∗0,28 ∗ 0 ln(0,013 ∗ 3,14 ∗ 10)) = 2,41; 1 4𝑟𝑐 ℎ2 𝑙0 С02 = ̅̅̅̅ (ln ( 𝜘 1 0,1 3 ) − 𝑚𝑙 ln(2𝜋𝑟0 𝑚)) = 0,46 (ln (4 ∗ 0,28) − 10∗0,28 ∗ 0 ln(0,013 ∗ 3,14 ∗ 10)) = 2,83. 10. По формулам определяем дополнительные сопротивления 𝑆1 и 𝑆2 : 𝑆1 = С1 (𝜌01 , ̅̅̅ ℎ1 ) + С2 (𝜌01 , ̅̅̅ ℎ2 ) + С01 = 3,85 + 7,94 + 2,41 = 14,19; 𝑆2 = С1 (𝜌02 , ̅̅̅ ℎ1 ) + С2 (𝜌02 , ̅̅̅ ℎ2 ) + С02 = 3,97 + 7,76 + 2,83 = 14,56. 11. Предельную депрессию ∆Рпр определяем по формуле: 4 ∆Рпр = = 𝜀 ∙ ℎ ∙ 𝑚𝑖𝑛(𝑞1 ∙ ∆𝜌1 , 𝑞2 ∙ ∆𝜌2 ) 𝑅0 𝑅0 ∗ 2 ∗ )2 (𝛽 ∙ [(𝜉 − 𝛼) (ln ( ) + 𝑆 ) + − 𝜉 (ln ( ) + 𝑆2 )] 1 (𝛽 − 𝛼)𝜉 ∗ 𝑟𝑐 𝑟𝑐 0,095 ∗ 0,075 ∗ 735 220 220 ∗ ((0,44 − 0,2)2 ∗ (ln ( ) + 14,19) + (0,7 − 0,44)2 ∗ (ln ( ) + 14,56)) (0,7 − 0,2) ∗ 0,44 0,1 0,1 = 65,82 Па. Результаты Одновременно предельный безводный и безгазовый дебит 𝑄 = 29,88 Предельная депрессия на пласт ∆Рпр = 65,82 Па. 5 м3 сут ; Приложение Таблица 1 - Плотности расходов предельных безводных и безгазовых дебитов q1 (α,β); q2 (α,β) 6 Таблица 2 - Определение ординаты нейтральной линии тока ξ* (α,β). Таблица 3 - Значение функции ψ(ρ,h) 7 Список использованной литературы 1. Телков А.П. Некоторые особенности эксплуатации нефтяных залежей с подошвенной водой. М: ВНИИОЭНГ, 1972. - 136с. 2. Телков А.П., Стклянин Ю.И. Образование конусов воды при добыче нефти и газа.-М.Недра, 1965. 8