Отбор корней при решении тригонометрических уравнений
реклама
Тема урока: Отбор корней при решении тригонометрических уравнений
Цели и задачи:
дидактические: обобщение и систематизация знаний учащихся по теме « Решение
тригонометрических уравнений»; закрепление основных понятий; систематизация умений и
навыков по применению способов отбора корней в тригонометрических уравнениях.
развивающие:
развитие
познавательного
интереса,
логического
мышления,
интеллектуальных способностей; формирование математической речи;
воспитательные: формировать эстетические навыки при оформлении записей в тетради и
самостоятельность мышления у учащихся.
Ход урока:
I. Организационный момент. Сформулировать цели и задачи урока.
II. Актуализация знаний учащихся.
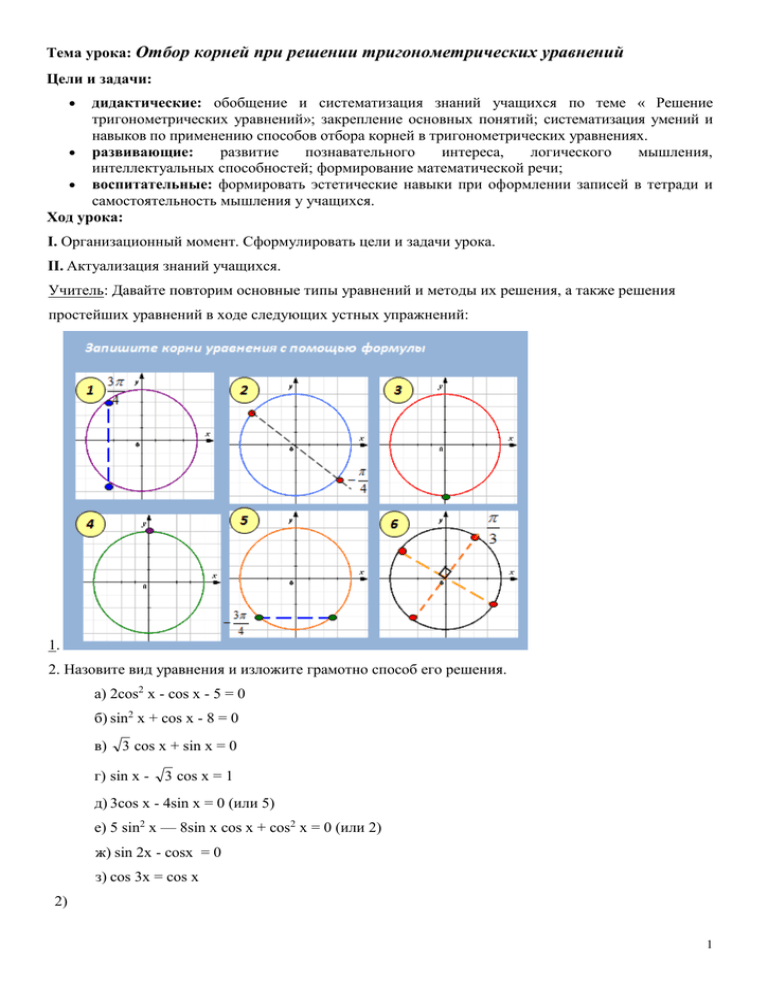
Учитель: Давайте повторим основные типы уравнений и методы их решения, а также решения
простейших уравнений в ходе следующих устных упражнений:
1.
2. Назовите вид уравнения и изложите грамотно способ его решения.
а) 2cos2 х - cos x - 5 = 0
б) sin2 х + cos x - 8 = 0
в) 3 cos х + sin x = 0
г) sin х -
3 cos x = 1
д) 3cos x - 4sin x = 0 (или 5)
е) 5 sin2 х — 8sin x cos x + cos2 x = 0 (или 2)
ж) sin 2х - cosx = 0
з) cos 3х = cos х
2)
1
Назовите несколько чисел из множества чисел вида:
2
n; 2k ;
6
2k ; (1) n
4
k
III. Переход к изучению нового.
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений
специфична. Лишние корни могут появиться вследствие того, что в процессе решения произошло
расширение области определения уравнения. Запись ответа тригонометрического уравнения часто
связана с понятиями объединения и пересечения множеств. Обычно при решении таких уравнений
получают серии корней, и в окончательном варианте ответ записывают в виде объединения этих
серий. Но как быть, если эти серии пересекаются? Сегодня мы на конкретных примерах рассмотрим
различные способы и приемы при выборе ответа. Для нас важность этой темы связана с тем, что
тригонометрические уравнения, в которых требуется провести отбор корней, часто встречаются в
тематических тестах ЕГЭ; это задание С1 с дополнительным условием.
При отборе корней в процессе решения тригонометрических уравнений обычно используют один
из следующих способов.
● Арифметический способ:
а) непосредственная подстановка полученных корней в уравнение и имеющиеся
ограничения;
б) перебор значений целочисленного параметра и вычисление корней.
● Алгебраический способ:
а) решение неравенства относительно неизвестного целочисленного параметра и вычисление
корней;
б) исследование уравнения с двумя целочисленными параметрами.
● Геометрический способ:
а) изображение корней на тригонометрической окружности с последующим отбором с учетом
имеющихся ограничений;
б) изображение корней на числовой прямой с последующим отбором с учетом имеющихся
ограничений.
Функционально-графический:
2
Выбор корней с помощью графика простейшей тригонометрической функции
Сегодня на уроке мы остановимся на наиболее часто применяемых способах отбора корней
и тех способах с которыми мы еще не сталкивались.
IV. Разбор примеров. Решение задач.
№1. . Отбор корней в тригонометрическом уравнении алгебраическим способом .
Изображение корней на тригонометрическом круге не всегда удобно, когда период меньше 2𝜋.
3x
Пример 1. cos 2 x cos
2
4
Решение.
Поскольку наибольшее значение функции y = cos t равно 1, уравнение равносильно системе
cos 2 x 1,
3x
cos 4 1;
x k , k Z ,
8n
x 3 , n Z ;
Решением уравнения является пересечение серий, то есть нам надо решить уравнение
8n
k
;
3
8n
k
;
3
Получаем
k 8t , n 3t , t Z
Итак,
x 8t , t Z .
Ответ : {8t / t Z }.
Пример 2.
x
x
cos sin x 2 sin 2 x cos x sin cos x 2 cos 2 0.
4
4
Решение.
sin( x ) cos x 2;
4
5x
1,
sin
4
cos x 1;
5x
2n, n Z ,
2
4
x 2k , k Z ;
2 8n
,n Z,
x
5
5
x 2k , k Z ;
Решением уравнения является пересечение серий, то есть нам надо решить уравнение
2 8n
2k
;
5
5
3
1 4n
;
5
5k 1 4n;
5k 1
n
;
4
k 1
k 1
nk
,
4
4
где
целое число.
k 1
Пусть
m,
4
k 4m 1,
n 5m 1.
тогда
Итак,
x 2 8m, m Z .
k
Ответ : {2 8m / m Z }.
№2. Отбор корней в тригонометрическом уравнении с помощью числовой окружности
(геометрический).
Проблему отбора корней, отсеивания лишних корней при решении тригонометрических уравнений
часто можно решить с помощью изображения чисел на тригонометрическом круге. В ряде случаев
этот прием более наглядный и убедительный.
Пример 1. cos x + cos 2x – cos 3x = 1.
Решение.
cos x – cos 3x – (1 – cos 2x) = 0,
2sin x sin 2x – 2sin2 x = 0,
2sin x (sin 2x – sin x) = 0,
4 sin x sin
x
3x
cos
0;
2
2
sin x 0,
sin x 0,
2
3x
cos
0;
2
x k , k Z
x n, n Z
2
3x
m, m Z ;
2
2
x k , k Z
x 2n, n Z
2m
, m Z;
x
3
3
Изобразим серии корней на числовой окружности. Видим, что первая серия включает в себя корни
второй серии, а третья серия включает в себя числа вида x 2k из корней первой серии.
4
0
Ответ : {2n;
3
2m
/ n, m Z }.
3
№ 3. Отбор корней в тригонометрическом уравнении с некоторыми условиями.
Изложенные выше способы отбора корней в тригонометрических уравнениях не всегда
применяются в чистом виде: выбор способа зависит от конкретных условий, но иногда эти способы
комбинируются.
Пример 1. Найти корни уравнения
sin 2x = cos x | cos x | , удовлетворяющие
условию x [0; 2𝜋].
Решение.
sin 2x = cos x | cos x |;
2sin x· cos x - cos x | cos x |=0;
cos x (2sin x - | cos x |)=0;
cos x 0,
cos x(2 sin x cos x) 0;
cos x 0,
cos x(2 sin x cos x) 0;
5
cos x 0,
x n, n Z ,
2
1
x arctg k , k Z ;
2
cos x 0,
1
x arctg m, m Z .
2
Определим решения систем с помощью числовой окружности.
2
2
1
2
y
2
1
2
2
x 2 n, n Z ,
1
x arctg 2m, m Z .
2
x arctg 1 2k , k Z .
2
3
,
Условию x [0; 2𝜋] удовлетворяют числа x , x
2
2
1
x arctg
2 (для второй системы).
x arctg
1
2 (для первой системы) и
3
1
1
Ответ : { ; ; arctg ; arctg }.
2 2
2
2
Пример 2. Найти все решения уравнения
1 sin 2 x 2 cos 3 x 0,
Решение.
ОДЗ: cos 3x ≥ 0;
2
2n 3 x
2
[ ;
принадлежащие отрезку
3
].
2
2n, n Z ;
6
6
2n
2n
x
,n Z;
3
6
3
Отметим ОДЗ на тригонометрическом круге:
c
o
s
x
5
6
2
6
< c
y
o
7
s
0
6
6
x
3
≥2
3 0
] принадлежит только один промежуток из ОДЗ, а именно
Отрезку [ ;
2
[
7 3
; ]. .
6 2
Решим уравнение и выберем корни, принадлежащие этому промежутку:
1 + sin 2x = 2cos2 3x ;
sin 2x = cos 6x;
sin 2x - cos 6x=0;
sin 2 x sin(
2 cos(
4
2
6 x) 0;
2 x) sin( 4 x
2 cos( 2 x
4
) sin( 4 x
4
4
) 0;
) 0;
cos( 2 x 4 ) 0,
sin( 4 x ) 0.
4
2
x
n, n Z ,
4 2
4 x k , k Z .
4
3 n
x 8 2 ,
x k , k Z .
16 4
Выберем корни, удовлетворяющие условию задачи.
Из первой серии:
7 3 n 3
,n Z;
6
8
2
2
28 9 12n 36 , n Z ;
19 12n 27, n Z .
7
11
.
8
Следовательно n=2, то есть
7 k 3
,n Z;
Из второй серии:
6 16 4
2
56 3 12n 72 , n Z ;
53 12n 69, n Z .
21
x
.
16
Следовательно n=5, то есть
11 21
Ответ : {
;
}.
8 16
x
VI. Итоги урока.
Итак, мы разобрали различные виды задач, где необходим отбор корней, рассмотрели несколько
способов такого отбора. Вы в дальнейшем можете применять любой из них. Урок показал, что вы
хорошо умеете решать уравнения различных типов (учитель выставляет оценки учащимся,
работавшим у доски, наиболее активным учащимся)
VII. Домашнее задание.
Закрепить дома виды задач.
1) Найдите все решения уравнения, принадлежащие указанному промежутку
a) cos 2x + sin x = cos2 x
на [0;2π]
б) sin x + cos x = 0
на [-π;π]
2) Найдите число корней уравнения из [-π;π]
3
3 sin 2
x sin 2 ( x) sin( 2 x)
2
3) Решите уравнение:
а) 2 cos 2 x sin x
б)*
2 cos x 1 cos x
8