К сети с напряжением U= 220В присоединен приемник энергии, имеющий

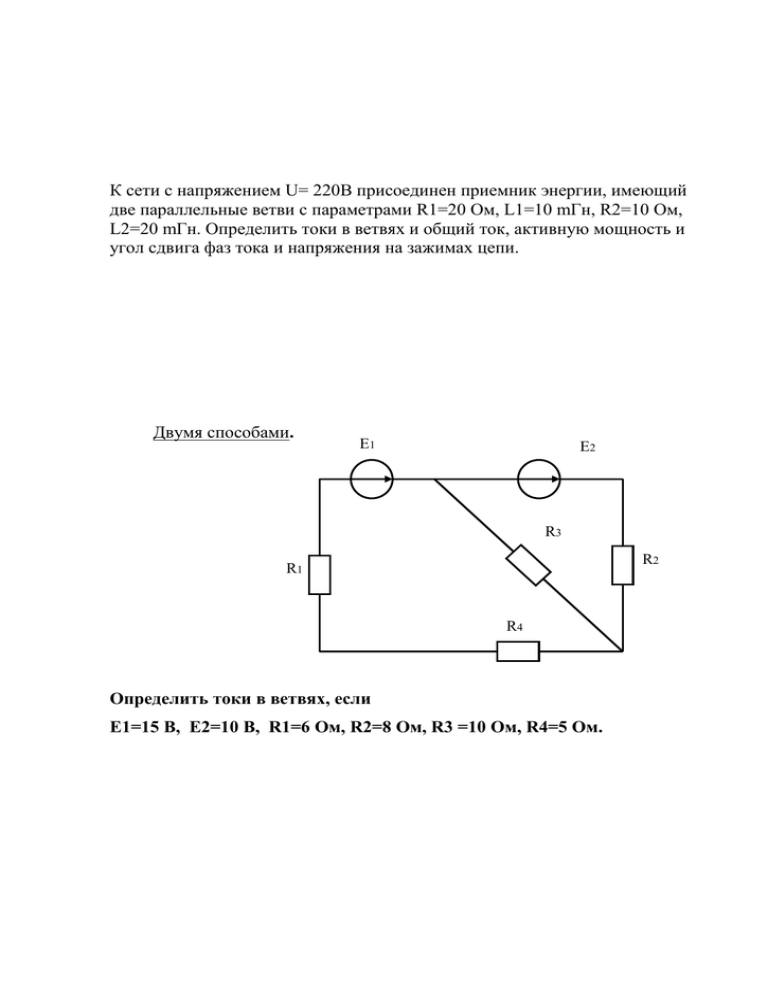
К сети с напряжением U= 220В присоединен приемник энергии, имеющий
две параллельные ветви с параметрами R1=20 Ом, L1=10 mГн, R2=10 Ом,
L2=20 mГн. Определить токи в ветвях и общий ток, активную мощность и
угол сдвига фаз тока и напряжения на зажимах цепи.
Двумя способами.
E1
E2
R3
R2
R1
R4
Определить токи в ветвях, если
E1=15 В, E2=10 В, R1=6 Ом, R2=8 Ом, R3 =10 Ом, R4=5 Ом.
Тема 2. Электрические цепи постоянного тока в установившемся
режиме
Лекция 6. Расчет простых резистивных схем.
1. Метод узловых потенциалов.
2. Метод контурных токов.
3. Метод наложения.
Литература: 1 Касаткин А.С. Электротехника: Учеб. для вузов /
А.С.Касаткин, М.В.Немцов. – 8-е изд., испр. – М.:
Издательский центр «Академия», 2003.
2 Теоретические основы электротехники: В 3-х т.
Учебник
для вузов. Том 1. – 4-е изд. /К. С. Демирчян, Л. Р.
Нейман,
Н. В. Коровкин, В. Л. Чечурин. – СПб.: Питер, 2004.
1 МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ
Анализ электрической цепи заключается, как правило, в расчете токов
в ветвях цепи, а в некоторых случаях – напряжений на элементах
электрической цепи. Структурные уравнения для проведения анализа
составляют на основе закона Ома, первого и второго законов Кирхгофа. При
этом число уравнений, требующих решения, равно числу неизвестных токов
в ветвях электрической цепи. Существуют приемы, позволяющие облегчить
постановку задач на математическом уровне. Учитывая структуру
конкретной цепи, можно так задать искомые функции и подобрать такую
форму для уравнений, что задачи анализа упростятся еще на этапе
формулировки. В частности, уменьшением количества неизвестных удается
сводить задачи к меньшему числу уравнений.
Известно несколько методов, позволяющих проводить анализ
линейных электрических цепей: метод узловых потенциалов, метод
контурных токов, метод наложения, метод эквивалентного генератора и др.
Далее приведены методики применения метода контурных токов, метода
узловых потенциалов и метода наложения. При расчете конкретных цепей
целесообразно выбирать тот метод, который позволяет получить меньшее
число уравнений, требующих решения. Если схема содержит q узлов и п
независимых контуров, то при выборе метода анализа необходимо
руководствоваться следующим:
при п < q – 1 предпочтительнее использовать метод контурных токов;
при п > q – 1 применяют метод узловых потенциалов.
Названные методы мы будем рассматривать применительно к
линейным цепям, содержащим, помимо активных элементов, только
сопротивления (проводимости) – пассивные элементы, для которых
справедлив закон Ома. Это ограничение не сильно сужает область
применения методов, поскольку именно для расчета цепей такого рода ими
чаще всего и пользуются. В частности, цепям с гармоническими токами,
составленным из всевозможных линейных элементов, в том числе из
емкостей, индуктивностей и индуктивно связанных элементов, сопоставляют
схемы замещения, которые состоят только из активных элементов и
сопротивлений.
1.1 Метод узловых потенциалов
Этот метод позволяет уменьшить число совместно решаемых уравнений
до q - 1, где q – число узлов схемы замещения цепи. Метод основан на
применении первого закона Кирхгофа и заключается в следующем:
1) один узел схемы цепи (любой) принимаем базисным с нулевым потенциалом. Такое допущение не изменяет значения токов в ветвях, так как ток в
каждой ветви зависит только от разностей потенциалов узлов, а не от
действительных значений потенциалов;
2) для остальных q – 1 узлов составляем уравнения по первому закону
Кирхгофа, выражая токи ветвей через потенциалы узлов;
3) решением составленной системы уравнений определяем потенциалы q - 1 узлов относительно базисного, а затем токи ветвей по
обобщенному закону Ома.
Рассмотрим применение метода на примере расчета цепи по рисунку 1,
содержащей q = 3 узла.
Рисунок 1
Узел 3 принимаем базисным, т.е. потенциал 3 = 0. Составляем уравнения
для узлов 1 и 2 по первому закону Кирхгофа:
узел 1
I1 + I3 + J1 = 0;
узел 2
I2 – I3 – J2 = 0.
Согласно закону Ома токи в ветвях равны
Подставив полученные выражения в уравнения для узлов и перенеся
слагаемые с источниками тока и напряжения в правую часть, окончательно
получим
или в матричной форме
Решение полученной системы уравнений методом подстановок или
численным методом на ЭВМ определяет потенциалы узлов 1 и 2, а,
следовательно, и токи ветвей.
2 МЕТОД КОНТУРНЫХ ТОКОВ
Метод контурных токов позволяет уменьшить число совместно
решаемых уравнений до К = В — Bj — q + 1 (где В – общее количество ветвей в
цепи, Bj – количество ветвей, содержащих источники тока) и основан на
применении второго закона Кирхгофа.
Рассмотрим сущность метода для расчета схемы цепи без источников тока,
т. е. при Bj = 0:
1)
выбираем К = В — q + 1 независимых контуров и положительных
направлений так называемых контурных токов, каждый из которых протекает
по всем элементам соответствующего контура.
Для планарных схем, т. е. допускающих изображение на плоскости без
пересечения ветвей, достаточным условием выделения К независимых контуров
является наличие в каждом из них хотя бы одной ветви, принадлежащей только
этому контуру;
2) для К независимых контуров составляем уравнения по второму закону
Кирхгофа, совместное решение которых определяет все контурные токи;
3) ток каждой ветви определяем по первому закону Кирхгофа как
алгебраическую сумму контурных токов в соответствующей ветви.
В качестве примера рассмотрим расчет цепи на рисунке 2, а с числом
ветвей В = 6, узлов q = 4, независимых контуров К = В — q +1 = = 6 — 4 + 1 = 3.
Выберем независимые контуры 1-3 и положительные направления контурных
токов в них I11, I22 и I33 (рисунок 2, б). В отличие от токов ветвей каждый
контурный ток обозначим двойным индексом номера контура. Уравнения по
второму закону Кирхгофа:
или в матричной форме
Рисунок 2
Решение системы уравнений методом подстановок или численными
методами на ЭВМ определяет контурные токи I11, I22, I33. Токи ветвей
(рисунок 2) находим по первому закону Кирхгофа: I1 = I11, I2 = I22, I3 = I33, I4 = (I11 + I33), I5 = I22 + I33, I6 = I11 - I22.
3 МЕТОД НАЛОЖЕНИЯ
Метод наложения (суперпозиции), применяемый для расчета
электрических цепей, основан на том, что любой источник ЭДС, находящийся
в одной из ветвей сложной электрической цепи, вызывает ток в каждой ветви
этой цепи. Вследствие этого ток в любой ветви электрической цепи численно
равен алгебраической сумме токов, вызываемых в этой ветви каждым из
источников ЭДС в отдельности.
Сущность метода состоит в том, что любая сложная электрическая
цепь, содержащая п источников ЭДС, заменяется п цепями, каждая из
которых содержит только один источник ЭДС в i-ой ветви (i = 1, n ), а
остальные источники исключаются с заменой их на сопротивления, численно
равные внутренним сопротивлениям этих источников. Для каждой
полученной электрической цепи находят токи во всех ветвях одним из
способов, после чего определяют токи в ветвях исходной электрической цепи,
как алгебраическую сумму токов в одноименных ветвях цепей, содержащих
по одному источнику ЭДС.
Рассмотрим пример использования метода наложения для расчета токов
в электрической цепи, представленной на рисунке 1.
Рисунок 1
Получим на основе исходной схемы (рисунок 1) две более простые
R1
R1
R2
I'2
I'1
I''2
R2
R1
I''3
I'3
E1
R2
I''1
R3
R3
E1
R3
E2
схемы (рисунок 2, а, б) и найдем токи в ветвях каждой из этих схем:
а
б
Рисунок 2
E2
I1' 
E1( R2  R3 )
E1

;
R1  R2R3 R1 R2  R2 R3  R1 R3
R2  R3
I '2  I1'
R3
E1 R3

;
R2  R3 R1 R2  R2 R3  R1 R3
I 3'  I1'
R2
E1 R2
;

R2  R3 R1 R2  R2 R3  R1 R3
I '2' 
E2 ( R1  R3 )
E2

;
R
R
R
R
 R2 R3  R1 R3
1
3
1
2
R2 
R1 R3
R3
E2 R3
I1''  I '2'

;
R1  R3 R1 R2  R2 R3  R1 R3
R2
E2 R2
I 3''  I '2'

.
R1  R3 R1 R2  R2 R3  R1 R3
Токи в ветвях схемы, приведенной на рисунке 1, при действии обоих
источников ЭДС будут равны:
I1  I1'  I1'' 
E1 ( R2  R3 ) E2 R3
;
R1 R2  R2 R3  R1 R3
E ( R  R ) E1 R3
I 2  I '2'  I '2  2 1 3
;
R1 R2  R2 R3  R1 R3
I 3  I 3'  I 3'' 
E1 R2  E2 R1
.
R1 R2  R2 R3  R1 R3