ЗАДАЧИ ДЛЯ РЕШЕНИЯ

ЗАДАЧИ ДЛЯ РЕШЕНИЯ
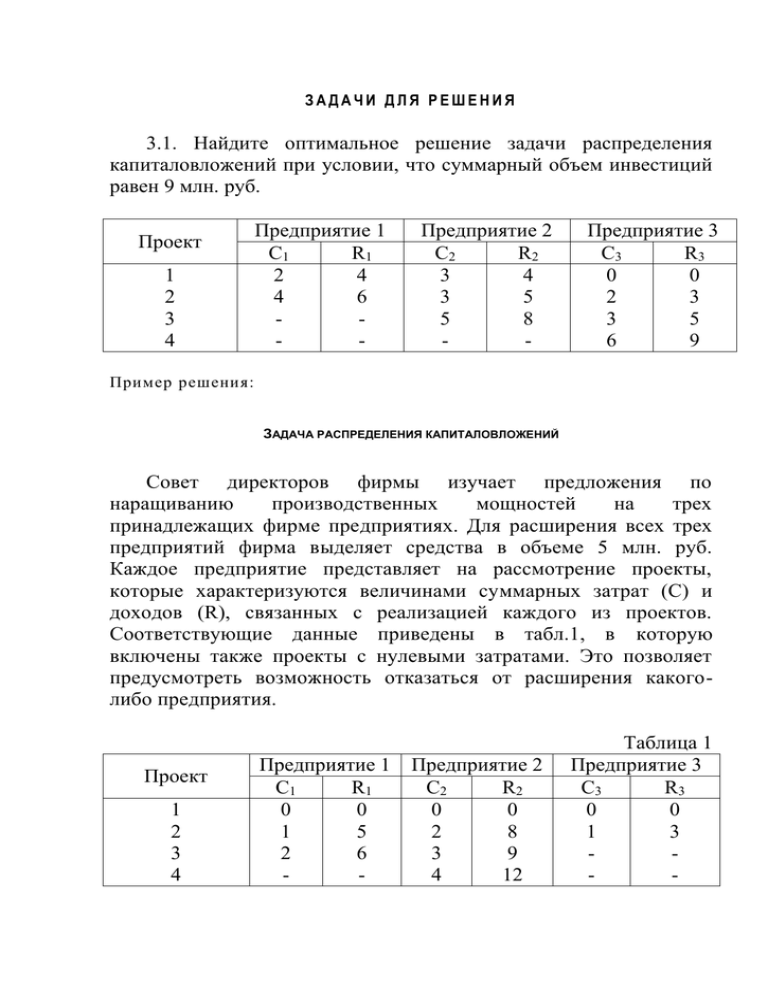
3.1. Найдите оптимальное решение задачи распределения
капиталовложений при условии, что суммарный объем инвестиций
равен 9 млн. руб.
Проект
1
2
3
4
Предприятие 1
C1
R1
2
4
4
6
-
Предприятие 2
C2
R2
3
4
3
5
5
8
-
Предприятие 3
C3
R3
0
0
2
3
3
5
6
9
Пример решения:
ЗАДАЧА РАСПРЕДЕЛЕНИЯ КАПИТАЛОВЛОЖЕНИЙ
Совет директоров фирмы изучает предложения по
наращиванию
производственных
мощностей
на
трех
принадлежащих фирме предприятиях. Для расширения всех трех
предприятий фирма выделяет средства в объеме 5 млн. руб.
Каждое предприятие представляет на рассмотрение проекты,
которые характеризуются величинами суммарных затрат (C) и
доходов (R), связанных с реализацией каждого из проектов.
Соответствующие данные приведены в табл.1, в которую
включены также проекты с нулевыми затратами. Это позволяет
предусмотреть возможность отказаться от расширения какоголибо предприятия.
Проект
1
2
3
4
Предприятие 1
C1
R1
0
0
1
5
2
6
-
Предприятие 2
C2
R2
0
0
2
8
3
9
4
12
Таблица 1
Предприятие 3
C3
R3
0
0
1
3
-
Цель фирмы состоит в получении максимального дохода от
инвестиций.
В рассмотренном примере каждому из предприятий ставится в
соответствие некоторый этап, поскольку требуется выбрать
оптимальный проект для каждого предприятия. Известно, что
этапы связаны между собой посредством ограничения на
суммарный объем капиталовложений. При построении модели
необходимо учесть эту связь таким образом, чтобы получить
возможность по отдельности решать подзадачи, соответствующие
каждому этапу, не нарушая при этом условия допустимости.
Введем следующие обозначения:
X1 – объем капиталовложений, распределенных на этапе 1.
X2 – объем капиталовложений, распределенных на этапах 1 и 2.
X3 – объем капиталовложений, распределенных на этапе 1,2,3.
Заметим, что конкретные значения X1 и X2 заранее не известны,
однако эти значения лежат в интервале между 0 и 5. Так как
затраты на реализацию каждого из проектов выражаются целыми
числами, значения X1 и X2 могут быть равны 0,1,2,3,4,5. с другой
стороны значение переменной X3 равно 5.
Пусть
 f1*(X1) – максимальный доход, полученный на этапе 1, при
заданном значении X1.
 f1*(X2) – максимальный доход, полученный на этапах 1 и 2,
при заданном значении X2.
 f1*(X3) – максимальный доход, полученный на этапах 1,2,3,
при заданном значении X3.
Тогда
рекуррентное
соотношение
динамического
программирования будет иметь следующий вид:
f 0* (X 0 )  0
f j* (X j )  max{ R j (k j )  f j*1 (X j1 )},
j  1,2,3 ,
берется по допустимым проектам kj.
Так как c j (k j )  X j  X j1 , следовательно,
где
максимум
X j1  X j  c j ,
(k j )  0 .
Откуда c j (k j )  X j .
Приведем результаты поэтапных расчетов на
рекуррентного соотношения для рассматриваемой задачи.
Этап 1. f1* (X1 )  max R 1 (k1 ), c1 (k1 )  X1 , k1  1,2,3 .
основе
X1
0
1
2
3
4
5
k1  1
0
0
0
0
0
0
R 1 (k1 )
k1  2
5
5
5
5
5
Оптимальное решение
k1  3
6
6
6
6
f1* (X1 )
0
5
6
6
6
6
k 1*
1
2
3
3
3
3
Этап 2. f 2* (X 2 )  max{ R 2 (k 2 )  f1* (X 2  c 2 (k 2 ))} , c 2 (k 2 )  X 2 ,
k 2  1,2,3,4 .
X2
0
1
2
3
4
5
k1  1
0+0=0
0+5=5
0+6=6
0+6=6
0+6=6
0+6=6
R 1 (k1 )
k1  2
k1  3
8+0=8
8+5=13 9+0=9
8+6=14 9+5=14
8+6=14 9+6=15
Оптимальное решение
k1  4
12+0=12
12+5=17
f 2* (X 2 )
0
5
8
13
14
17
k *2
1
1
2
2
2,3
4
Этап 3. f3* (X3 )  max{R 3 (k 3 )  f 2* (X3  c3 (k 3 ))} , c 3 (k 3 )  X 3 ,
k 3  1,2 .
X3
5
{R 3 (k 3 )  f 2* (X3  c3 (k 3 ))}
k3  1
k3  2
0+17=17
3+14=17
Оптимальное решение
f 3* (X 3 )
17
k *3
1,2
Максимальный доход от инвестиций в объеме 5 млн. руб.
составит 17 млн. руб. Оптимальное решение можно найти
непосредственно из приведенных таблиц, используя соотношение
X j1  X j  c j (k j ) . Причем сначала рассматривается таблица,
полученная на этапе 3, затем на этапах 2 и 1. В результате получим
следующие оптимальные наборы проектов для этапов 1,2 и 3 –
[{2,4,1}, {3,2,2}, {2,3,2}].